你遇到過這“尷尬”的一幕嗎?

? 浙江省寧波市鎮海區尚志中學 翁海芳

在講解反比例函數習題的過程中,筆者曾兩次遇到“尷尬”的一幕,課堂上有學生表示:“老師,您的方法太煩了,我有簡便方法.”雖然我硬著頭皮講完,但學生之后展示的方法確實比我的簡單,作為教師的我都有點汗顏.在之后的章節測試中,筆者發現大多數學生雖然在課堂上對那位同學的方法贊嘆不已,但最終還是運用了老師講的方法解決問題.這一經歷促使筆者深入思考“通性通法”與“特解巧法”的關系.

1 第一次教學經歷

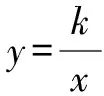
圖1

大部分學生都會通過聯立方程,求出A,B的坐標,思維障礙在于怎樣用所設的字母表示三角形的邊,因此,筆者順著學生的思維,重點落腳解決障礙,給出通常的解法.

圖2

對于y=2x+6,令y=0,得x=-3,則C(-3,0).

本來學生順著老師的思路,找到了解題的路徑,感覺頗有收獲,但此時一位學生給出了他的方法,打破了這一氛圍.

解法2：如圖3,連接AA′,交x軸于點H,記一次函數y=2x+6的圖象與y軸的交點為E,連接EH,AO,A′E.

圖3

由反比例的性質,可得BC=AE,則S△A′BC=S△A′AE=4.

由點A,A′關于x軸對稱,得S△A′AE=2S△HAE.

顯然學生的解法更加簡單,其他同學都向他投去欽佩的目光,而對老師的“笨”辦法則頗為不屑.

課后反思:本題的關鍵是表示△A′BC的面積,筆者講解的方法是設反比例函數圖象上點A,B的坐標,用點A,B,C的橫坐標表示出三角形的高,用點A的縱坐標表示三角形的底,再利用面積公式求出三角形面積,進而結合題意建立等量關系,利用函數與方程的知識求出k的值.

學生的解法首先立足模型“如圖4,任意的直線與反比例函數圖象相交,都有BC=AE”,再運用“同(等)底等高的兩個三角形面積相等”的性質來解題,最后利用k的幾何意義求值.這里用到了轉化的思想.

圖4

2 第二次教學經歷

圖5

學生會設反比例函數圖象上點的坐標,但是不會用所設的點表示其他的點,因此筆者講解了如下的方法.

圖6

某學生給出的方法如下:

圖7

課后反思：筆者講解的方法是典型的坐標法,用坐標表示三角形的底和高,再利用面積公式列出方程.坐標法是解決反比例函數問題的通用方法,所設坐標的點要有利于表示其他有用的點的坐標.在設點的坐標時,可以設橫坐標,也可以設縱坐標,可以同時設出橫、縱坐標,利用坐標表示線段的長,找到恰當的等量關系建立關于面積的方程.

圖8

3 關于通性通法與特解巧法的思考

3.1 通性通法是基礎

通性通法是解決問題的普適方法,簡單來說,就是指數學的主要性質與主要思想方法,是延伸性、輻射性較強的數學知識與思想方法.“通”指數學知識與數學方法中最重要、最通用的東西.例如,求反比例函數比例系數k的值,一般有兩種通法:(1)求出圖象上的點的坐標,再運用待定系數法求k值;(2)設特殊點的坐標,進而表示出其他有用的點的坐標,再尋找等量關系建立方程求k值.通性通法易于理解、掌握,但有時過程繁瑣,除嚴謹、仔細的態度外,還需具備一定的運算能力、推理能力、思維能力和綜合能力.

3.2 特解巧法靠積累

特解巧法是指針對某個具體問題的結構特征,觸類旁通地運用所學知識,通過一定的發散性思維和創造性思維而獲得的特殊方法.這種方法適應面比較窄,理解的人覺得非常簡單,不理解的人甚至不得其門而入,它著眼于提升和創新.平時在反比例函數的教學中挖掘并補充的很多知識,比如,圖4、圖8的模型等,利用這些知識點解決問題就是特解巧法,一般比通性通法方便.關鍵在于平時積累,形成知識網絡,并能靈活匹配.

當今數學教學的主導精神是科學化、體系化,通性通法自然被視為解題的首選,但若只要求學生學習通性通法,一定程度會限制他們的創造力和個人表達的空間;而寄希望于向學生灌輸解題技巧,鋌而走險追求需要苛刻的天資才能支撐起來的創造性思維,則有悖可靠性的原則.只有兼顧通解和巧解,學生的數學素養才能得到更好的發展.二者就像雕刻家手中的兩種工具,通解如同鑿子,用于揭示問題的大致輪廓,巧解如同刻刀,在細節的刻畫上更加精確,缺少鑿子和刻刀中任何一個,雕像終究是有缺憾的.