核心素養導向下的單元章末復習教學與思考
——以人教A版“空間直線、平面的垂直”復習課為例

蔣亞軍, 任偉芳

(1.寧波市第四中學,浙江 寧波 315016;2.寧波市教育局教研室,浙江 寧波 315100)

2023年6月,寧波市教育局教研室組織了以“新課標新教學下的高中數學章末單元復習課研討”為主題的課堂教學比賽活動,課題為“空間直線、平面的垂直”的復習課,共有17位選手以同課異構的形式進行角逐.筆者依據單元整體教學的理念,結合授課內容特點和學生認知水平,構建了一節以鱉臑模型中尋找垂直的歷程為線索、展現數學思想方法和研究思路的課堂.筆者執教的“借助鱉臑模型整合空間垂直——以‘空間直線、平面的垂直’復習課為例”得到了評委老師和學生的一致好評,榮獲一等獎.現將筆者參賽的教學設計和課后反思整理成文,與同行分享,不當之處敬請批評指正.

1 教材分析

“空間直線、平面的垂直”是人教A版《普通高中教科書·數學》(以下統稱“高中《數學》”)(必修第二冊)第八章“立體幾何初步”中最后一個單元的內容.因此,這節復習課不僅能夠綜合提升線線垂直、線面垂直及面面垂直學習的效果,還承擔了垂直這一單元小結課的功能,對進一步完善學生的立體幾何知識體系起著重要的作用.類比空間直線、平面的平行關系的研究,得到空間直線、平面的垂直關系的研究思路,體會研究幾何對象的基本方法,感受研究空間位置關系“直觀感知→操作確認→推理論證→度量計算”的一般研究思路.

2 教學目標

從知識層面看,學生學習了線面垂直、面面垂直的判定定理和性質定理,了解了異面直線所成角、線面角和二面角的定義和求法;從方法層面看,學生能夠類比空間直線、平面平行關系的研究思路和路徑,對空間直線、平面垂直關系進行研究;從單元層面看,通過對幾何對象的研究方法及空間位置關系的研究思路的學習體會,學生能夠提升認識和探索空間圖形的能力.課堂中形成了本節課的知識網絡和素養落實結構圖,如圖1所示.

基于以上分析,確立本節復習課的教學目標為:

1)通過直觀感知生活中的垂直現象,利用推理論證并應用線面垂直、面面垂直的判定定理和性質定理,理解這些定理之間的邏輯關系,利用定義會找異面直線所成角、線面角和二面角;

2)體會“直觀感知→操作確認→推理論證→度量計算”的研究思路;

3)落實數學抽象、直觀想象、邏輯推理、數學建模等核心素養.

3 教學重點與難點

教學重點:通過鱉臑模型回顧線面垂直、面面垂直的判定定理和性質定理.

教學難點:利用鱉臑模型發現線線角、線面角、二面角之間的數量關系.

4 教學過程

4.1 折紙游戲抽象模型

課堂引入分為兩個環節:一是折紙游戲,事前準備好紙片,教師邊演示邊講解,學生完成鱉臑的制作;二是用PPT投影高中《數學》(必修第二冊)第158頁的例8、第160頁的例10和第163頁的練習7,引導學生從3個熟悉的例題、習題中抽象出鱉臑模型.

師:這些都是我們熟悉的教材上的例題和習題,觀察題目中的圖形(如圖2),它們有什么共同特征?

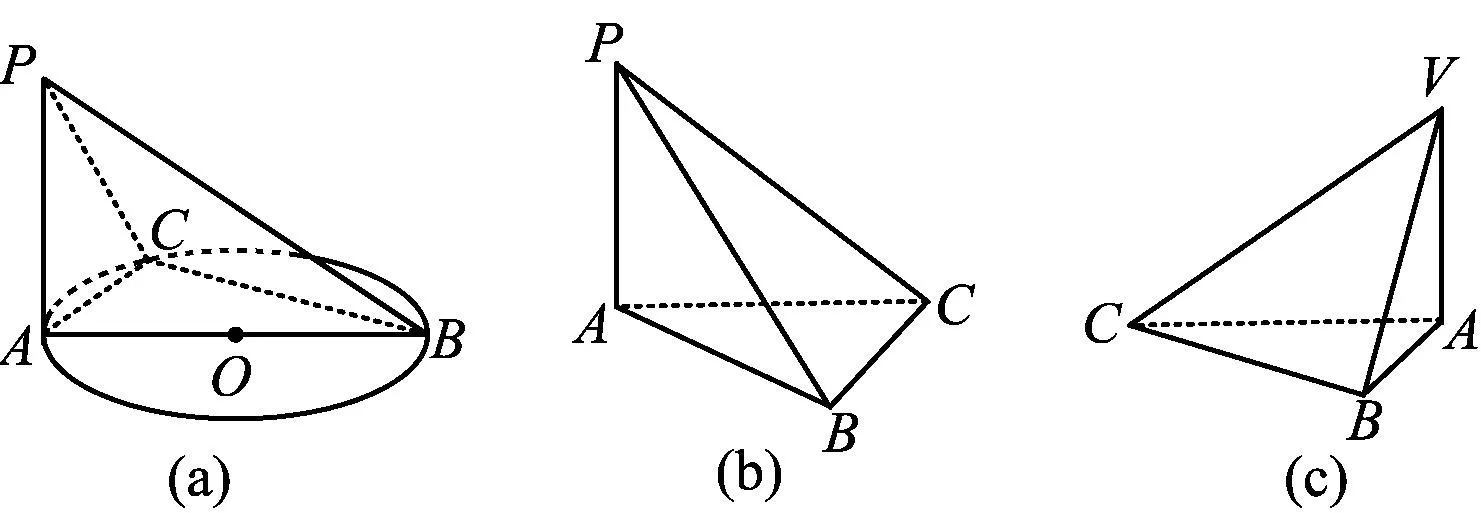
圖2

生1:都是由4個直角三角形組成的三棱錐.

師:很好,這種底面是直角三角形,有一條側棱垂直于底面,垂足不是直角頂點的三棱錐稱為鱉(biē)臑(nào).

早在公元一世紀左右,我國古代的數學名著《九章算術·商功》指出:斜解立方,得兩塹堵.斜解塹堵,其一為陽馬,其一為鱉臑.陽馬居二,鱉臑居一,不易之率也.

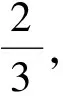
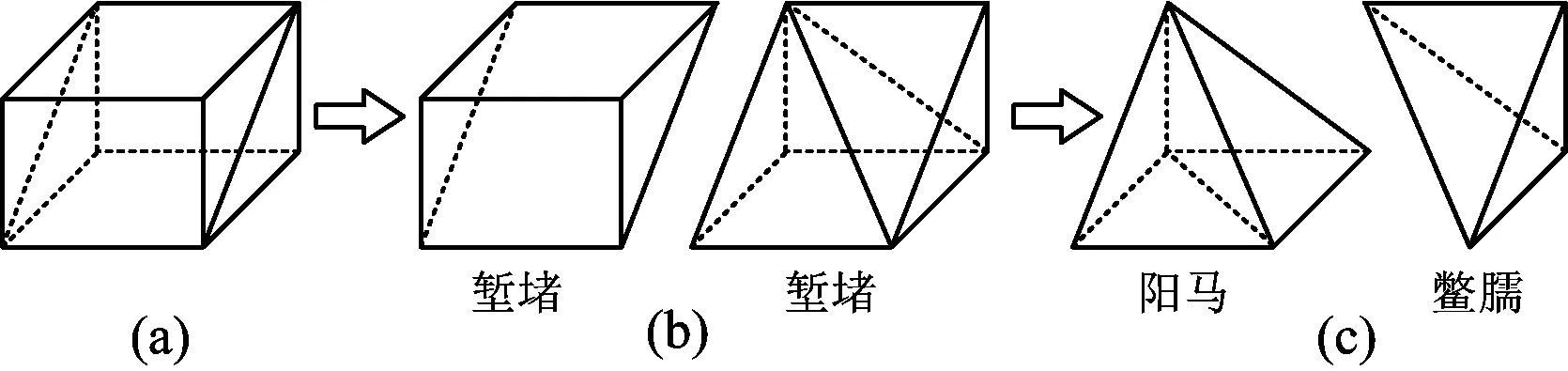
圖3

鱉臑不僅可以由長方體切割得到,也可以把它補形成長方體.本節課以鱉臑為載體,回顧整理空間直線、平面的垂直關系.

設計意圖從傳統文化折紙游戲引入,激發學生的興趣,學生參與度高.折出鱉臑后有兩個方面的意圖:一方面,使學生感受到數學是有趣的、好玩的;另一方面,抓住學生的好奇心,使學生產生“鱉臑有什么用?”的疑問,為本節課的學習提供順其自然的需求.通過展示學生熟悉的例題和習題,引導學生觀察3個圖形,歸納總結共同特征,并抽象得到鱉臑模型.借助數學名著《九章算術·商功》介紹鱉臑的由來,配合動畫演示,激發學生的學習興趣和民族自豪感,能夠體會“既可以通過長方體切割得到鱉臑,又可以將鱉臑補形回到長方體”.

4.2 鱉臑的判定

問題1如圖4,在三棱錐A-BCD中,AB⊥BC,AB⊥DC,BC⊥DC,你能發現哪些線面垂直?哪些面面垂直?為什么?

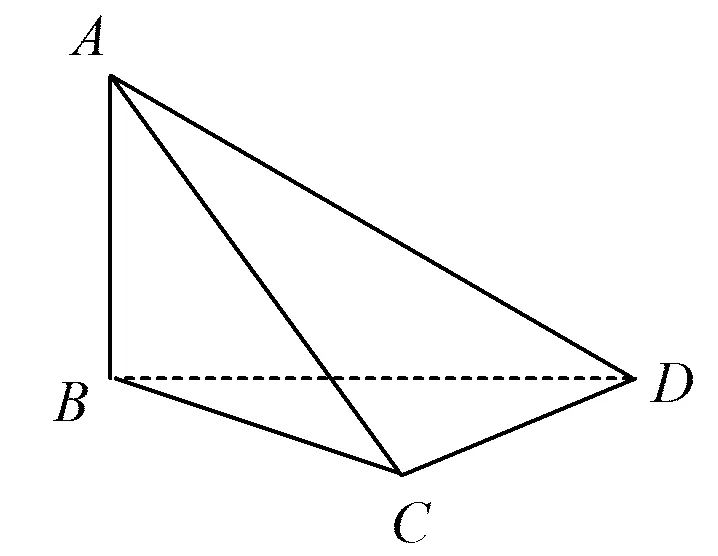
圖4

追問1三棱錐A-BCD是一個鱉臑嗎?

追問2如果選定AB⊥平面BCD,你能添加條件讓它還是鱉臑嗎?

追問3如果平面ABC⊥平面BCD,平面ABD⊥平面BCD,可以判定它是鱉臑嗎?

設計意圖問題1的設置可以幫助學生回顧線面垂直、面面垂直的判定定理和性質定理.學生邊回答,教師邊板書符號和圖形語言,最后呈現線線垂直、線面垂直及面面垂直之間相互轉化的框架圖.為接軌新高考模式下的結構不良題型,設置開放性問題(追問2),在PPT屏幕上展示各種垂直條件讓學生選擇,然后再加以證明.學生在AB⊥平面BCD的前提下,容易想到添加條件“BC⊥CD”“AC⊥CD”或“平面ABC⊥平面ACD”.問題的解決體現了執果索因的思想,有利于落實學生邏輯推理的核心素養,形成知識的網絡結構圖.追問3可以通過直觀演示直角三角板任意轉動,發現不能保證BC⊥CD,故不能判定為鱉臑.

4.3 鱉臑的性質

問題2在判定三棱錐A-BCD是一個鱉臑后,你能得到哪些關于垂直方面的結論呢?

學生小組討論后,得到以下結論:

異面直線垂直(1組):AB⊥CD;

線面垂直(2組):AB⊥平面BCD,DC⊥平面ABC;

面面垂直(3組):平面ABC⊥平面BCD,平面ABD⊥平面BCD,平面ACD⊥平面ABC;

相交垂直(4組):AB⊥BC,AB⊥BD,DC⊥BC,DC⊥AC.

4.4 鱉臑的應用

圖5

(2008年浙江省數學高考理科試題第14題)

問題4如圖6,在三棱錐P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D為線段AC的中點,E為線段PC上一點.

1)求證:PA⊥BD;

2)求證:平面BDE⊥平面PAC;

3)當PA∥DE時,求三棱錐E-BCD的體積.

(2017年北京市數學高考文科試題第18題)

設計意圖選擇以鱉臑為模型的高考真題,使學生有熟悉感.問題3主要體現補形的思想,降低思維難度,使學生能快速完成解答.在問題4中若能找到鱉臑模型,則利用鱉臑的性質可以快速解決選擇題、填空題,但解答題還是需要嚴格證明.其中第3)小題的解決可以直接應用體積公式,也可以通過比例關系將鱉臑補成長方體.

4.5 鱉臑再探究

問題5鱉臑模型不僅包含垂直關系,還包含數量關系——空間角和距離.如圖7,請你找出直線AD與平面BCD所成的角,以及二面角A-CD-B的平面角.

圖7

追問4當二面角A-CD-B為45°時,直線AD與平面BCD所成角的取值范圍是多少?

追問5當直線AD與平面BCD所成角為45°時,二面角A-CD-B的取值范圍是多少?

追問6設∠ADB=θ(線面角),∠ADC=θ1(線線角),∠BDC=θ2(射影角),∠ACB=φ(二面角).這些角的三角函數有什么關系呢?

4.6 小結提升

師:請結合本節課的學習,回答下面的問題:1)本節課復習了哪些知識?2)按照怎樣的路徑對鱉臑進行研究?3)學習過程包含哪些數學思想方法以及核心素養?

學生總結出以下結論:

1)知識內容:借助鱉臑模型回顧了直線、平面的3種垂直關系的相互轉化;

2)研究路徑:定義→判定→性質→應用;

3)思想方法:模型思想、轉化思想、建模思想、執果索因;

4)核心素養:數學抽象、直觀想象、邏輯推理、數學運算.

師:最后用一首打油詩小結.鱉臑模型在手,三種垂直都有;線面垂直溝通,推理驗證直觀.

5 教學反思

1)單元復習課要制定以素養為導向的教學目標.

鱉臑不僅包含了立體幾何中點、線、面的各種位置關系,有著豐富的垂直關系作為定性判斷的依據,是討論空間直線、平面的垂直關系及其相互轉化的非常好的載體;還包含了立體幾何千變萬化的空間角,為破解定量計算以及揭示幾何體基本結構與本質規律帶來可能.在鱉臑的判定環節,出現了線面垂直、面面垂直的判定定理和性質定理,形成垂直關系相互轉化的結構圖,把零碎的知識串聯起來.這樣處理的效果要比直接給出定理再進行應用要好,更有利于學生理解和掌握,也關注到了文字語言、符號語言和圖形語言的相互轉化.在鱉臑的應用和再探究環節,精選問題,滲透切割與補形的數學思想,通過一題多解,學生能熟練地應用鱉臑模型來解決數學問題.在問題設置上接軌新高考出現的新題型——結構不良試題,具有開放性,有利于學生思維的發散,形成從直觀感知到嚴格證明的科學研究思路.

2)單元復習課要整體關聯知識方法和核心素養.

復習課的定位應該是“基礎知識的掌握、基本技能的提高、基本思想方法的落實、基本活動經驗的積累”[1].單元內容一般由基礎知識、思想方法和核心素養加以串聯.單元結構化教學要注重知識結構的“明線”和思想方法與核心素養的“暗線”[2].本節課的“明線”是圍繞鱉臑展開的,從抽象出鱉臑模型開始,沿著定義、判定、性質、應用一步步展開,這也是研究幾何對象的基本方法.類比平行關系的學習,沿用從簡單到復雜的思路,既要掌握線面垂直、面面垂直的判定定理和性質定理,又要通過定義異面直線所成角、線面角和二面角來刻畫空間圖形的關系.為后續的定量計算以及空間向量的學習做鋪墊,體會研究幾何對象的基本方法,感受研究空間位置關系“直觀感知→操作確認→推理論證→度量計算”的一般研究思路.本節課的“暗線”從數學思想和核心素養兩個方面展開.從教材中的例題和習題抽象出鱉臑模型,體現了模型思想,鱉臑的判定的證明過程中有執果索因思想的體現,開放性問題的設置以及切割與補形的統一突出了轉化與化歸的思想,落實了數學抽象、直觀想象、邏輯推理和數學運算等核心素養.

3)單元復習課要引導學生感悟數學文化的價值.

《普通高中數學課程標準(2017年版2020年修訂)》指出,數學課程內容要培育數學核心素養,繼承與弘揚中華優秀傳統文化,堅定文化自信;要注重數學文化的滲透,不斷引導學生感悟數學的科學價值、應用價值、文化價值和審美價值.中華優秀傳統數學文化走進高中數學課堂強調古為今用,提升學生數學學習的文化內涵,促進核心素養的綜合發展.本節課創設適合的教學問題情境,引入“鱉臑”模型,啟發學生思考,引導學生把握數學內容的本質,體會古代數學家對人類的貢獻.本節課圍繞鱉臑模型,把本單元的知識有效地整合在一起,既有定性的判斷,又有定量的計算.采用傳統文化——折紙游戲引入,吸引了學生的注意,借助學生已有的知識儲備,促進學生積極主動地參與本節課的學習,突出學生的主體地位,關注學生基本活動經驗的積累.對我國古代數學名著《九章算術·商功》的介紹,一方面,體現了古代數學家的成就,有利于增強學生的民族自豪感;另一方面,體現了數學源于生活,又服務于生活,要做一個生活的有心人,用數學的眼光觀察現實世界.這樣的設計,既豐富了課堂的數學文化,又激發了學生的學習興趣.

總之,單元整體教學視角下的章末復習課的研究與實施,需要在教學實踐中不斷探索和創新.學生的學習是一種特殊形式的探究,是在教師的指導下有目的、有計劃、系統性地進行知識建構,學生在較短的時間內學習數學知識的過程[3].教師要遵循知識的整體性、情境的貫穿性、思維的連續性、邏輯的連貫性和方法的系統性,通過設置符合學情的問題,引導學生體悟數學對象的研究思路和研究方法,促進學生在學習活動中提高必備品質和關鍵能力,逐步形成正確的價值觀,從而實現由“學會”到“會學”再到“樂學”的轉變.