主動配電網源網荷儲一體化協調優化模型研究

楊勇虎，魏 華，吳文輝

（1.東莞城市學院，廣東 東莞；2.易事特集團股份有限公司，廣東 東莞）

引言

在傳統電力系統里“源”、“網”、“荷”和“儲”是相互獨立的，當某一環節出現異常其他部分能夠快速調整，避免整個系統崩潰，從而提高電力系統的穩定性[1]。對分布式電源、儲能以及負荷等方面進行靈活控制對于主動配電網的應用水平有重要影響。諸多專家學者對主動配電網的協調優化策略進行研究與實踐，研究集中在配電網運行規劃中綜合考慮這些主動管理策略，但主動配電網調度領域仍然存在終端能源利用率較低等問題[2]。基于此提出一種主動配電網源網荷儲一體化協調優化模型，實現更高效、更穩定的電力傳輸。

1 主動配電網源網荷儲一體化協調優化模型設計

1.1 分析主動配電網節點參數

主動配電網的規模通常比較大，因此含多個節點，基于此本研究對主動配電網的節點參數分析。

基于傳統的節點功率方程分析，該方程如下[3]。

式中，i 和j 分別為主動配電網中的兩個節點，n 為主動配電網中的節點總數量，Pi為節點i 的有功需求，Qi為節點i 的無功需求，Vi和Vj分別為節點i 和節點j的電壓幅值，Gij為兩個節點的電導，Bij為兩個節點的電納，θij為兩個節點間的電壓相角差。

該方程中包含正弦函數和余弦函數，導致求解難度大[4]。對該方程調整，采用ZI 方程對其進行線性表達如下。

式中，P（Vi）為主動配電網節點i 的有功功率需求，Q（Vi）為主動配電網節點i 的無功功率需求，P0為主動配電網負荷初始有功需求，Q0為主動配電網負荷初始無功需求，CZ、C0以及CI均為常數，且三者之間呈現為求和為1 的關系，V0為節點初始假定電壓。

對主動配電網的節點參數分析，采用幅值相角的方法對節點的電流參數計算如下。

式中，Ii為節點i 的電流相量，V'i為節點i 的實部電壓。

式中，將節點的實部電壓取值設定為1，節點的虛部電壓為0，節點虛部電壓忽略不計，不納入計算。

由于在主動配電網的節點中，電流在節點中呈現流動的形態，對節點處的電流參數等效計算如下。

式中，Ii為節點i 的等效電流參數。

1.2 構建主動配電網協調優化模型

對主動配電網的協調網架拓撲結構分析，對主動配電網節點開關的切換次數計算如下。

式中，S 為主動配電網節點開關切換次數，μij為開關切換后的節點狀態，μij0為開關切換前節點狀態。

式中，μij0共包括兩種取值，當其取值為0 時，為主動配電網節點在原有的饋線中處于斷開的狀態，當其取值為1 時為主動配電網節點在原有的饋線中處于閉合的狀態。

公式（5）主動配電網節點開關的切換次數較多情況下，產生的損耗較高，對切換次數參數約束，公式如下。

式中，Smax為主動配電網節點開關一天最大切換次數。主動配電網協調優化模型的配網輻射約束如下。

式中，τij和τji為兩個不同的目標約束變量，取值均有“0”和“1”兩種。其中一個取值為“1”時，則為另一個節點的母節點，I^i為主動配電網協調優化模型目標約束，Iijmax為主動配電網支路最大電流。

2 實驗

2.1 實驗準備

建立主動配電網的仿真模型，采用IEEE-33 節點標準型主動配電網，該配電網包含33 個節點，節點分布見圖1。

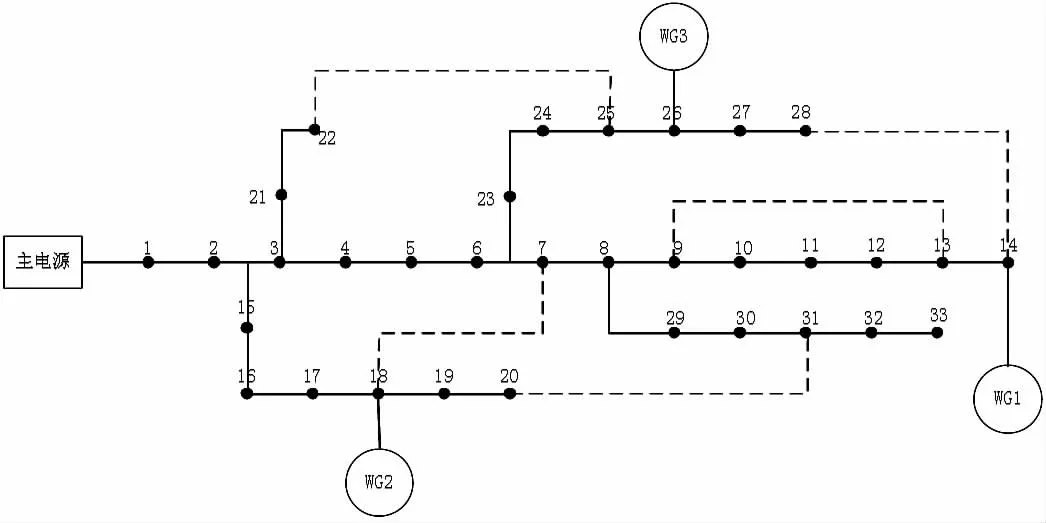
圖1 IEEE-33 節點主動配電網

圖1，IEEE-33 節點主動配電網中，黑色實線為初始狀態為閉合的支路，黑色虛線表示部分節點間的聯絡線，于14 節點、18 節點及26 節點處分別含一個分布式電源。在仿真環境進行實驗見表1 和表2。

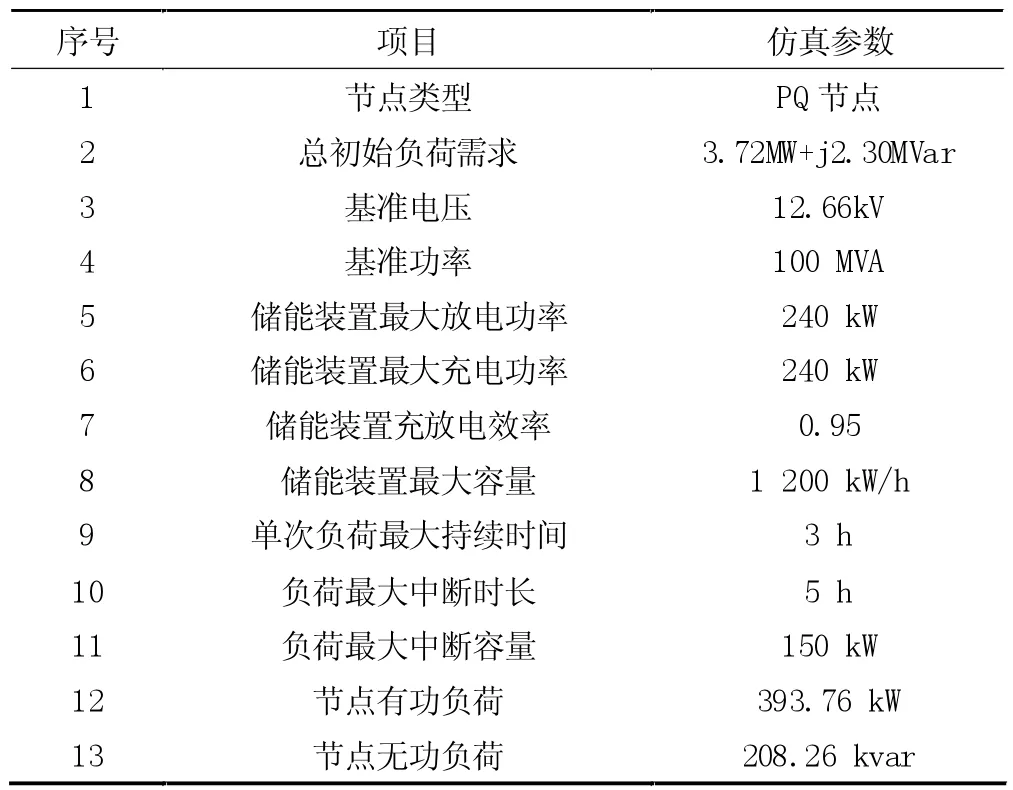
表1 主動配電網實驗環境仿真參數

表2 仿真實現環境

上對主動配電網的源網荷儲數據進行模擬，并對涉及到的模型及方法實現。

2.2 實驗結果及分析

為體現本文模型的實踐應用可行性，采用基于Fisher 時段劃分的主動配電網源網荷儲協調優化方法1 及基于電力物聯網狀態感知下的主動配電網源網荷儲協調優化方法2 為實驗對比方法。本文優化模型的方法3。應用三種方法在仿真環境測試，得到不同方法下主動配電網源網荷儲協調優化結果見圖2。

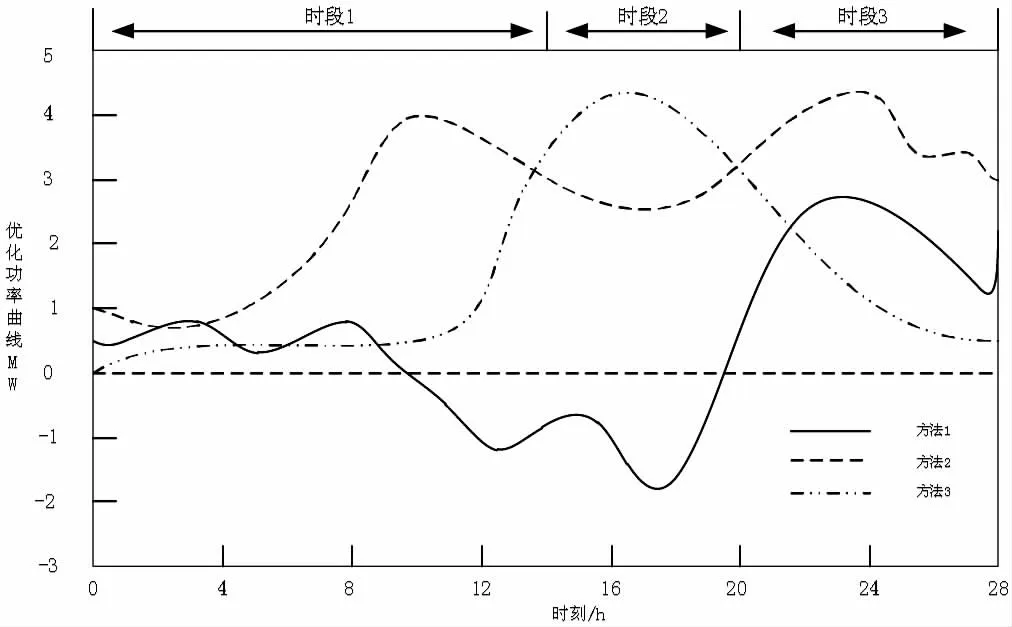
圖2 不同方法主動配電網源網荷儲協調優化結果

圖2，13～20 的時段2 階段中，優化的主動配電網功率較高，其余時間的功率較低，與設置的主動配電網的配電需求參數的變化曲線高度一致，對電能利用率較高。其他兩種方法中，均未呈現與配電需求保持一致的曲線波動變化，在三個時段均出現多次波動，得到的結果對電能的利用率不理想。

按照當前國家標準基準電價，根據圖1 優化結果對三種協調優化方法協調成本對比見表3。

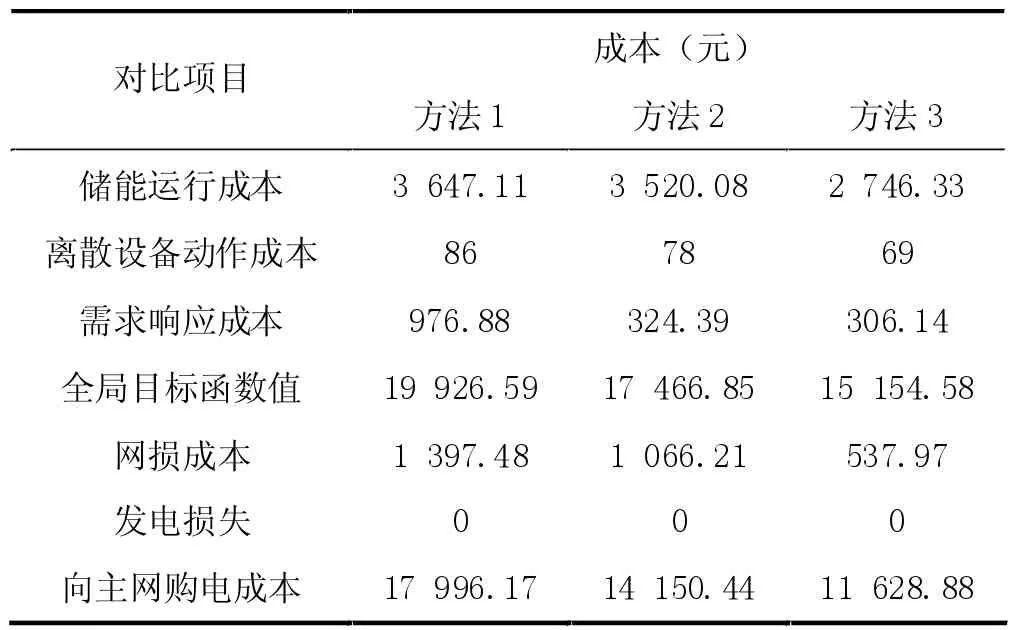
表3 不同協調優化方法成本對比結果

圖2 和表3 可知，所提的主動配電網源網荷儲一體化協調優化模型能有效對主動配電網中的各項能源進行優化調度，所需調度成本低，具備較高的實踐應用價值。

結束語

主動配電網源網荷儲一體化優化模型研究，可提高電力系統的穩定性，推動能源轉型和電力行業的可持續發展。結合其他領域的先進技術，有望為電力行業帶來更多的創新和發展。