基于機器學習的小容值MLCC 容量模型的研究

劉夢穎

（福建火炬電子科技股份有限公司，智能制造中心，福建 泉州）

引言

小容值（標稱容量≤68pF）多層瓷介電容器（MLCC）廣泛應用于各種電子設備中，如手機、電腦等，用于降低噪聲干擾，提高設備的性能和穩定性[1]。但小容值MLCC的容量精度要求非常嚴格，在生產過程中，材料批次、工藝及設備等因素造成的容量波動[2]，往往會超過其容量精度要求，所以小容值MLCC 一直存在容量命中率低的問題[3]。

本文提出采用機器學習算法，將小容值MLCC 的制備參數（如：瓷粉型號、批號，內電極型號、批號，需求電容量，介質層厚度，有效面積等）作為輸入量，將印刷層數作為輸出量，建立模型，確定印刷層數與電容量之間的函數關系，把預測得到的印刷層數與實際生產使用的印刷層數進行對比分析，評估模型用于預測小容值層數設計的可行性。

1 小容值MLCC 電容量設計

MLCC 的主要結構包含陶瓷介質層、內電極金屬層以及外電極三個部分，其結構如圖1 所示，一個MLCC就相當于若干個鄰近內電極組成的平板電容器并聯，因此電容器電容量計算公式[4]如下：

圖1 多層陶瓷電容器的基本結構

ε0- 真空介電常數，8.854×10-12（F/m）；

ε- 瓷粉介電常數；

S- 正對面積；

d- 介質層厚度；

n- 印刷層數，n-1 為有效的電極層數。

2 機器學習

機器學習[5]是指尋找數據中的模式（規律）并將發現的規律對未來做出預測。本文小容值MLCC容量模型建立流程如下：（1） 收集數據：收集小容值MLCC 生產過程數據與對應的電容量；（2） 因素分析：分析不同變量與電容量之間的相關性，提取電容量（Y）的相關影響因子（Xi）；（3） 整理數據：對收集的數據進行轉換、補缺、組織等，并定義和執行與數據相關的任務；（4） 數據挖掘：以“Y”為目標變量，“Xi”為影響因子，選用合適的算法對數據進行挖掘和呈現，反復迭代提升預測精度，篩選獲得符合要求的模型；（5） 預測驗證：采用預留數據去預測“Y”，并將預測值與實際“Y”進行對比驗證，評價模型的準確性；（6） 模型轉化：將獲得的最佳模型設計成可視化界面，方便用戶使用。

3 結果與分析

3.1 第一次運算結果

首次收集小容值MLCC 生產數據共170 條，包括各工序工藝信息（變量共有35 個）及電容量，對有效的電極層數（n-1）進行轉換，對多個數據點進行均值處理。采用5種算法模型進行訓練，并提供各個模型的均方誤差（MSE），均方誤差是指參數估計值與參數真值之差平方的期望值，表示平均的預測誤差大小，值越小越好。從結果中，決策樹模型具有最低的MSE，表現較好。然后采用最佳模型預測隨機預留數據的“Y”值，結果預測精度在±10%以內的預測準確度為65%，未達到預期目標。

3.2 第二次運算結果

首次設計預測準確度較低的原因：（1） 選取的影響因子可能缺失部分重要因子；（2） 部分區域段的數據較少，模型訓練不夠充分。針對原因（1），通過層層剖析，燒結作為關鍵工序，直接影響陶瓷介質層與內電極漿料的致密化過程，形成有效的MLCC 結構體，對產品電容量具有決定性作用[6]，因此增加與燒結相關的參數：燒后介質膜厚、燒結溫度和Y 軸燒結收縮率作為影響因子。針對原因（2），分析數據發現小容值MLCC 共選用兩種內電極型號生產，所以按內電極型號劃分數據，再分別進行算法預測。

兩種電極數據的運算最佳模型分別為極度隨機樹（ExtraTrees） 和隨機森林（Random Forest），MSE 分別為7.60 和3.75，從圖2 可以看出，內電極1 采用極度隨機樹模型，大多數樣本上的預測與實際非常接近。內電極2 采用隨機森林預測值的趨勢與實際趨勢相同，但是數值偏差較大。然后分別采用最佳模型預測隨機預留數據的“Y”值，內電極1 和內電極2 預測精度在±10%以內的預測準確度分別為60%和62.5%，未達到預期目標。

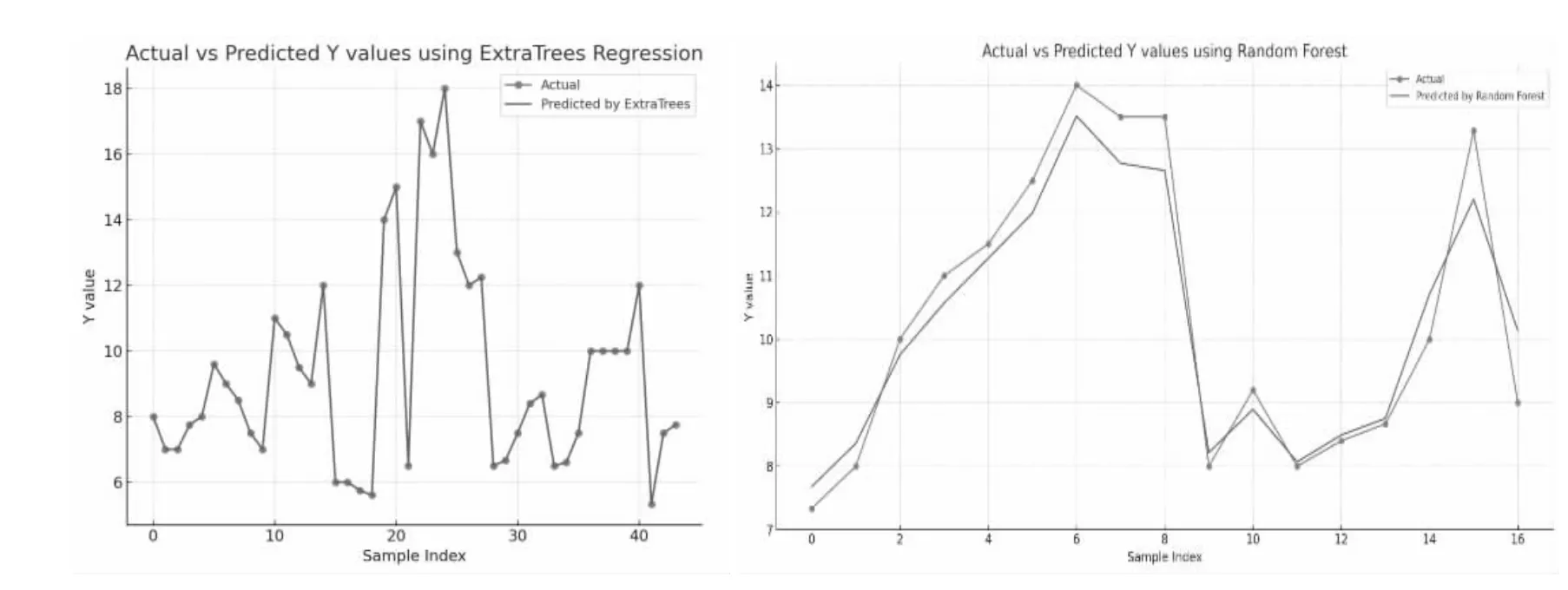
圖2 第二次運算模型預測值與實際值對比圖

3.3 第三次運算結果

按照內電極型號劃分數據源運算結果的預測準確度并沒有提升，再次分析原因：（1） 預測值對應訓練集里相似結構的數據條太少；（2） 預測值對應的產品結構與訓練集的不同。因此考慮細分數據源的區域段，使模型能夠充分訓練，提高預測精度。第三次提取四個分段的數據源：（1） 內電極1 容量3pF 以下；（2） 內電極1 容量（4～20）pF；（3） 內電極2 容量3pF 以下；（4）內電極2 容量（4～20）pF，對應的運算最佳模型分別為極度隨機樹、極度隨機樹、K 最鄰近和AdaBoost 迭代算法，MSE 分別為6.12、5.12、1.80 和2.96。然后分別采用最佳模型預測隨機預留數據的“Y”值，四個分段數據預測精度在±10%以內的預測準確度分別為28.57%、83.33%、50%和75%，部分數據段的預測準確度有明顯的提高，但3pF 以下數據預測準確度未達到預期效果。

3.4 第四次運算結果

3.4.1 產品結構劃分

根據前面運算結果，有如下規律：跨越的影響因子越多，相互干擾越大，預測準確性越低，詳見表1。因此本文參照相應的設計規范，將采用相同正對面積S，相同介質層厚度d 的產品進行歸類，共18 種產品數據段，如圖3 所示。

表1 預測準確性與跨越影響因子關系

圖3 小容值MLCC 線性回歸模型運算結果

當固定容量計算公式里的S 和d，這樣電容量=ε*k*（n-1），k=S*ε0/d。將電容量設為因變量y，電極層數（n-1）設為自變量x，電極層數與電容量的關系將進一步簡化為線性回歸模型，即y=a+bx。

3.4.2 運算結果

對相同結構的產品數據段進行線性回歸模型運算，同時匯總線性回歸模型的決定系數R2、擬合精度、預測精度等結果，如圖3 所示。

3.4.3 反向預測與控制

若限定因變量y 在某區間（y1，y2）內，應控制自變量x在什么范圍內，使得當x1＜x＜x2時，在給定置信度（1-α）下，可保證y1＜y＜y2，這就是控制。

公式中：n：樣本量；

SE：樣本數據的標準誤差；

xi：第i 個數據中的x值；

x：隨機變量xi的平均值。

本文已知容量y0及容量上下限（y1，y2），反向預測電極層數x0及計算在置信度95%要求下可保證容量在規定精度要求內的電極層數x的范圍。根據圖3 的運算結果反向計算得出每個產品數據段對應控制公式中的各因子數值，然后設計基于機器學習的小容值MLCC 層數設計預測工具，輸入需求容量和容量允許偏差，工具會根據公式計算并輸出印刷層數的預測推薦值，并輸出在置信度95%下，可保證容量在規定的精度要求范圍內的印刷層數范圍。

3.4.4 驗證

基于機器學習的小容值MLCC 層數設計預測工具，本文設計5 種驗證方案，如圖4 所示，依據工具預測層數安排投產印刷層數。實際生產時，小數層是通過在印刷層之間增加空白層以達到調整容量的目的，因此小數層一般是分數（譬如1/3 層=0.333 層）。各方案生產的小容值MLCC 電容量如表2 所示，電容量最小值，平均值以及最大值均在容量要求值范圍內，容量命中率達到100%，可以說基于線性回歸算法設計的小容值MLCC層數設計工具預測效果很好，在制備工藝參數保持穩定的前提下，通過小容值MLCC 層數設計預測工具模型，用需求容量預測印刷層數，可以應用于實際當中指導小容值MLCC的生產，提高容量命中率。

表2 小容值MLCC 層數設計預測工具驗證結果

圖4 小容值MLCC 層數設計預測工具驗證方案

4 結論

本文主要介紹采用機器學習預測小容值MLCC 容量模型的建立過程，最終采用線性回歸模型表達小容值MLCC的印刷層數和電容量之間的關系，決定系數R2為0.903～1.000，均大于0.9，層數擬合精度誤差均在±5.5%以內，預測精度在±5%以內的預測準確度達到94%，說明回歸預測模型中電容量與電極層數之間擬合程度較好。依據工具預測層數安排投產驗證，各方案（印刷層數）生產的電容量均滿足要求，容量命中率達到100%。因此，在制備工藝參數保持穩定的前提下，通過小容值MLCC層數設計預測工具模型，用需求容量預測印刷層數，可以用于指導小容值MLCC 的實際生產，提高容量命中率。