基于節(jié)點相似性的二階鏈路預測方法

劉 臣，王嘉賓

（上海理工大學 管理學院，上海 200093）

0 引言

現(xiàn)實世界中的很多復雜系統(tǒng)，如社交關系、交通運輸、生物系統(tǒng)、信息系統(tǒng)等，都可以建模為網(wǎng)絡。其中，將某個實體對象表示為節(jié)點，它們之間的交互關系表示為連邊（或鏈接）。然而，由于收集數(shù)據(jù)時人為統(tǒng)計的失誤或者數(shù)據(jù)本身有隱私設置等原因，構建的網(wǎng)絡并不一定反映真實的數(shù)據(jù)，使得收集網(wǎng)絡數(shù)據(jù)的完整結構變得尤為困難［1-2］。因此，根據(jù)觀察到的網(wǎng)絡信息預測缺失的節(jié)點或者鏈路是一項極為重要的工作，其對于補全相對完整的網(wǎng)絡具有重要意義［3］。

鏈路預測的目的是根據(jù)觀察到的鏈路和節(jié)點屬性估計兩個節(jié)點之間存在鏈路的可能性，如果兩個節(jié)點彼此相似，則它們之間也更有可能存在鏈路。鏈路預測方法主要有三大類：基于相似性的方法、基于概率和最大似然的方法以及基于降維的方法。基于相似性的方法是基于鄰域結構計算節(jié)點之間的相似度，分別從局部和全局的角度計算。局部相似度指標通常使用節(jié)點的近鄰和節(jié)點度的信息進行計算，包括共同鄰居指標（CN）［4］、優(yōu)先鏈接指標（PA）［5］等，計算復雜度低，在聚類系數(shù)低的稀疏網(wǎng)絡中很難得到高的準確率。全局相似度指標如Katz 指標［6］和SimRank 指標［7］是利用網(wǎng)絡的整個拓撲信息進行計算，計算復雜度較高且不適用于大型網(wǎng)絡。基于概率［8-9］和最大似然［10-11］的方法依賴網(wǎng)絡的層次結構判斷節(jié)點連邊的可能性，操作復雜且耗時，不適用于真實的大型網(wǎng)絡。面對高維度的難題，研究者將網(wǎng)絡嵌入和矩陣分解技術作為降維技術，也將其用于鏈路預測。DeepWalk 和Node2vec 網(wǎng)絡嵌入方法通過保留節(jié)點的鄰域結構，將圖中的高維節(jié)點映射到較低維度的表示空間［12-13］。Berahmand 等［14］將網(wǎng)絡結構和節(jié)點屬性相結合，引入新的鏈接預測隨機游走模型用于解決屬性網(wǎng)絡中的鏈路預測。Menon 等［15］將結構鏈接預測問題建模為矩陣補全問題，并使用矩陣分解進一步求解。

鏈路預測在不同的網(wǎng)絡類型中都有相應研究，在不同的領域也都有成熟的應用，例如在社交網(wǎng)絡中從大量的注冊用戶中為單個用戶自動推薦熟人；在科學合作網(wǎng)絡中預測哪些作者或團體在未來可能合作，以更好地了解一些研究領域的發(fā)展情況。這些研究針對兩個節(jié)點之間是否存在鏈路展開，本文探討網(wǎng)絡中的二階鏈路該如何預測，在計算節(jié)點對之間的相似性時，識別一個中間節(jié)點，同時預測涉及中間節(jié)點的兩條鏈接。本文學習基于相似性的鏈路預測算法，提出了一種基于節(jié)點相似性的二階鏈路預測方法，用于為用戶或者合作者雙方找到可以實現(xiàn)通信的第三方，還可以在社交網(wǎng)絡中為兩個本不相識的用戶識別出可能各自與他們相熟的目標用戶，為雙方用戶搭建溝通的橋梁。一個更有意義的工作是監(jiān)控恐怖主義網(wǎng)絡中的隱藏關系［16］，推測不同的恐怖分子或團體是經(jīng)由哪一個團體或個人聯(lián)絡，即使他們之間的交互沒有被直接觀察到，以據(jù)此做好安全防范工作。

在鏈路預測中，一個相當大的挑戰(zhàn)是數(shù)據(jù)稀疏性。如果網(wǎng)絡中的數(shù)據(jù)過于稀疏，則無法從簡單的公共鄰居數(shù)量或其他相關變體指標中提取出有價值的相似性信息［17］，此時只考慮局部信息可能會導致較差的預測。顧秋陽等［18］使用高階路徑作為判別特征對復雜網(wǎng)絡中的缺失鏈接進行有效預測；LYU 等［19］使用較長的路徑（長度大于2 的路徑）度量節(jié)點相似性。但由于涉及高階信息，計算過程中會產生很多噪聲，不利于相似度計算。Liao 等［20］發(fā)現(xiàn)基于相關性的方法在計算基于高階路徑的相似度時非常有效，不會受噪聲影響，進一步與資源分配方法相結合，對稀疏網(wǎng)絡和密集網(wǎng)絡都適用。目標網(wǎng)絡的稀疏性會導致一個問題，即一條鏈路的先驗概率通常都很小，很難建立統(tǒng)計模型。與傳統(tǒng)的鏈路預測任務不同，本文提出在網(wǎng)絡中實現(xiàn)二階鏈路預測，為一對已知節(jié)點識別中間節(jié)點并補全二階鏈路。本文構造新的計算指標用于識別節(jié)點，并構建了一個二階可達網(wǎng)絡以篩選可能的節(jié)點，一方面減小了計算復雜度，另一方面也緩解了數(shù)據(jù)稀疏性。利用鄰接矩陣構造二階可達矩陣，記錄網(wǎng)絡中的二階鏈路信息。相比于原始網(wǎng)絡中傳達的一階信息，二階可達矩陣所對應的二階可達網(wǎng)絡保留了原始網(wǎng)絡中所有的二階鏈路，有助于實現(xiàn)本文的二階鏈路預測。

1 問題描述

令G=(V，E)表示無權無向網(wǎng)絡，V是網(wǎng)絡G中節(jié)點的集合，節(jié)點數(shù)為|V|，E是網(wǎng)絡G中邊（或鏈接）的集合，邊數(shù)為|E|。將不相連的節(jié)點對vi與vj記為(vi，vj)，節(jié)點對之間的相似性定義為sim(vi，vj)，該值越大，節(jié)點對之間越有可能存在鏈接。因此，可以將sim(vi，vj)看作節(jié)點對之間是否存在鏈接的評分。網(wǎng)絡G的鏈接用鄰接矩陣A表示，當節(jié)點vu與vw之間存在鏈接時，鄰接矩陣中的元素auw值為1，否則為0。如果節(jié)點vu和vw之間存在鏈接，則這兩個節(jié)點互為鄰居節(jié)點，稱vu和vw之間是一階可達的。如果節(jié)點vu和vw不直接相連，存在節(jié)點vk使之形成二階鏈路vu-vk-vw，則稱vu和vw之間是二階可達的，互為二階鄰節(jié)點。

二階鏈路預測任務通過在一對已知節(jié)點的二階鄰域交集中確認最有可能分別與節(jié)點對存在鏈路的同一個節(jié)點身份，實現(xiàn)已知節(jié)點對之間的二階鏈路預測。如圖1 所示，在可觀測節(jié)點集{v1，v2，v3，v4，v5，v6，v7，v8}中，v1的二階鄰域節(jié)點集為{v3，v5，v8}，v6的二階鄰域節(jié)點集為{v3，v8}。從節(jié)點對(v1，v6)的二階鄰域交集{v3，v8}中比較它們各自與節(jié)點v1、v6的相似性，如sim(v1，v3)，sim(v3，v6)，若與v1、v6均有較大相似性的節(jié)點為v3，則可以確認v1、v6之間的一條二階鏈路為v1-v3-v6。

Fig.1 Second-order link prediction task圖1 二階鏈路預測任務

2 網(wǎng)絡中的二階鏈路預測

本文利用節(jié)點相似性進行二階鏈路預測，首先將目標節(jié)點的搜索范圍縮小至節(jié)點對的二階鄰域，然后基于相似性指標sim(vi，vj)進行加工，求得與節(jié)點對均有很高相似度的節(jié)點，以確認目標節(jié)點的身份，從而實現(xiàn)二階鏈路預測任務。圖2描述了網(wǎng)絡中的二階鏈路預測過程。

2.1 二階可達網(wǎng)絡

當網(wǎng)絡中的部分鏈接不被觀察到或網(wǎng)絡中的部分鏈接被去除，剩下的網(wǎng)絡結構偏向于稀疏圖，這不利于提取節(jié)點的鄰居信息，因此首先處理數(shù)據(jù)稀疏問題。網(wǎng)絡中的鏈接用鄰接矩陣A表示，對鄰接矩陣A進行變換操作，得到矩陣A2，其中每個元素就是節(jié)點vi和vj之間長度為2 的路徑的數(shù)目。將其對角線元素置0，非零元素的數(shù)值替換為1，得到一個0-1 矩陣，稱之為二階可達矩陣。也即當節(jié)點對vi與vj之間存在二階鏈路時，二階可達矩陣中的元素值為1，否則為0。根據(jù)二階可達矩陣所描述的節(jié)點間的鏈接信息構建新的無向網(wǎng)絡，稱之為二階可達網(wǎng)絡G'。

本研究主要介紹了組合可調式Halo -骨盆固定支具的設計及初步臨床應用結果，仍存在一些不足：①樣本量少，尤其是針對結核性脊柱后凸畸形方面需要進一步積累臨床病例；②缺乏與其他類型脊柱牽引技術的對照研究；③Halo -骨盆固定支具剛性牽引作用力大，容易導致盆針切割及變形，盆針的穿針方式、牽引策略及器材設計有待進一步改善。

當一對節(jié)點是二階可達，但它們之間的鏈路不被檢測到時，中間節(jié)點的身份是未知的。受基于相似性的鏈路預測算法啟發(fā)，兩個存在鏈接的節(jié)點相似性必定極高，且它們之間存在公共鄰居節(jié)點，則目標節(jié)點與已知節(jié)點在網(wǎng)絡中可能是二階可達的。因此，可以從已知節(jié)點對的二階可達節(jié)點集的交集內找到目標節(jié)點，而候選目標節(jié)點的集合在二階可達網(wǎng)絡中可見。

2.2 二階鏈路預測指標

當去除網(wǎng)絡中的一部分鏈接時，網(wǎng)絡變得稀疏，由于基于節(jié)點局部信息的相似性指標不能計算沒有共同鄰居的節(jié)點之間的相似性［17］，因此鏈接預測指標在稀疏網(wǎng)絡中很難得到高的準確率。為了解決這一不足，本文考慮將目標節(jié)點的搜索范圍放在二階可達網(wǎng)絡內，不僅降低了計算復雜度，而且預測準確率也在一定程度上得以提高。在網(wǎng)絡中分別與節(jié)點vi、vj存在鏈路的節(jié)點很有可能不止一個，是否為同一個目標節(jié)點還需作進一步判斷。本文擬在可能與節(jié)點vi或節(jié)點vj存在鏈路的多個節(jié)點中，找到可能同時與節(jié)點vi、vj存在鏈路的目標節(jié)點。

基于節(jié)點相似性，本文提出二階鏈路預測指標，用于在已知節(jié)點對的二階鄰域內尋找公共一階鄰節(jié)點。指標如下：

其中，sim(x，y)是度量節(jié)點相似度的一個指標，評分值越大，節(jié)點對之間存在鏈路的可能性越大，它可以是任意一個普通的鏈接預測指標。Γ2(vi)指節(jié)點vi的二階可達節(jié)點集，v是vi、vj的二階可達節(jié)點集交集中的節(jié)點。

2.3 基礎鏈路預測指標

基于節(jié)點局部信息的相似性指標如CN 指標、AA 指標、RA 指標、PA 指標可以計算節(jié)點間的相似度，因此借助這類指標完成二階鏈路預測任務。

CN（Common Neighbors）指標即共同鄰居指標，基于共同鄰域大小度量節(jié)點間的相似性，如果兩個未知鏈接的節(jié)點i和j共同的鄰居越多，則它們之間產生鏈接的可能性就越大［4］。相似度計算如下：

其中，Γ(i)為節(jié)點i的鄰居節(jié)點的集合；Γ(j)為節(jié)點j的鄰居節(jié)點的集合。

其中，kz為節(jié)點z的度數(shù)。

JC（Jaccard Coefficient）指標是基于CN 指標，考慮節(jié)點度的影響所產生的同樣基于共同鄰居思想的相似性指標。

AA（Adamic-Adar）指標在CN 指標的基礎上考慮了共同鄰居間的權重差異，認為共同鄰居的節(jié)點度越小，對相似度的貢獻越大，為度較小的鄰居節(jié)點分配更高的權重［22］。

PA（Preferential Attachment）指標認為節(jié)點i和j產生新鏈接的可能性與節(jié)點度的乘積成正比［5］。

2.4 樣本構造

針對網(wǎng)絡中滿足最小度為4 的目標節(jié)點，按一定比例剔除一部分與之相連的鏈接，將被剔除鏈接的目標節(jié)點之外的節(jié)點兩兩組合構造正節(jié)點對。在網(wǎng)絡的二階可達矩陣中，節(jié)點度大于2 且元素值為0 所對應的節(jié)點對為負節(jié)點對。

3 實驗與結果分析

3.1 數(shù)據(jù)集

本文使用4 個真實網(wǎng)絡的數(shù)據(jù)對二階鏈路預測算法性能進行評估。Cora 是一個引文網(wǎng)絡，其中節(jié)點代表機器學習方面的論文，只有當其中一篇論文被另一篇論文引用時，兩篇論文之間才會形成一條邊緣，該網(wǎng)絡由2 708 個節(jié)點和5 429 條邊組成。Citeseer 同樣是引文網(wǎng)絡，由3 312個節(jié)點和4 715 條邊組成。Washington 和Texas 包含兩所大學網(wǎng)站中的網(wǎng)頁引用，節(jié)點和邊分別代表網(wǎng)頁和網(wǎng)頁之間的引用。Washington 由230 個節(jié)點和446 條邊組成，Texas 由187 個節(jié)點和328 條邊組成。4 個網(wǎng)絡的統(tǒng)計信息如表1所示。

Table 1 Statistical information of four networks表1 4個網(wǎng)絡的統(tǒng)計信息

3.2 實驗相關設置

3.2.1 參數(shù)設置

每次獨立實驗中，去除目標節(jié)點的鏈接比例為0.2，將數(shù)據(jù)集按照0.7、0.1、0.2 的比例劃分為訓練集、驗證集和測試集。

3.2.2 評估指標

由于隨機因素的存在，根據(jù)二階鏈路預測指標計算得到的最大指標值所對應的節(jié)點并不一定是真正缺失的目標節(jié)點。Liben-Nowell 等［23］通過幾個相似性度量提取兩個節(jié)點之間的相似性。根據(jù)這些相似性為每對節(jié)點分配排名，然后將排名較高的節(jié)點對指定為預測鏈接。因此，本文將得到的計算指標由大到小排序，對應得到一系列可能的缺失節(jié)點{v1，v2，v3，…}。為了驗證該指標的有效性，給定一個閾值，設置為k，在這一系列節(jié)點的前k個節(jié)點中檢驗是否真正找回目標節(jié)點并關注找到節(jié)點的精確率，進而評判該指標的預測性能。

本文采用的評估指標是AUC 和Precision，AUC 用于評估是否識別到缺失的鏈路，Precision 用于評估在閾值內識別到真實目標節(jié)點的精確度。AUC 在鏈接預測中的定義為從測試集和負樣本中各隨機取一條鏈接，比較這兩條鏈接的分數(shù)。假設在n次獨立比較中，測試集中的鏈接比負樣本中的鏈接擁有更高分數(shù)的次數(shù)為n1，兩者擁有相同分數(shù)的次數(shù)為n2，則AUC 的計算公式為：

精確率（Precision）指在識別為真鏈接的樣本中真正是真鏈接的樣本所占比例，精確率越高，說明模型效果越好。

3.3 結果分析

本文基于普通鏈路預測算法的相似性指標，利用RA、JC、AA、PA 這4 項指標作為基準鏈路預測指標幫助實現(xiàn)本文提出的二階鏈路預測方法，并在4 個真實網(wǎng)絡中檢驗其效果。表2 和表3 分別列出了相應的AUC 值和Precision值，其中每個網(wǎng)絡的最優(yōu)值用加粗表示。由表2 可知，各項基準指標在Citeseer 網(wǎng)絡上均表現(xiàn)良好；JC 指標和PA 指標可以分別在其中兩個網(wǎng)絡上實現(xiàn)較好的性能。在Washington 和Texas 網(wǎng)絡中，JC 指標相比其他指標得到的AUC值提升了0.29%～17.15%；在Cora 和Citeseer 網(wǎng)絡中，PA 指標相比其他指標得到的AUC 值提升了1.92%～2.05%。但相比而言本文提出的方法在Texas 網(wǎng)絡上表現(xiàn)并不好，在Washington 網(wǎng)絡上的表現(xiàn)也不顯著，這與網(wǎng)絡本身的結構有關。當網(wǎng)絡規(guī)模較小時，按一定比例剔除部分鏈接會使網(wǎng)絡結構發(fā)生很大改變，容易造成采樣不充分，因此在這樣的網(wǎng)絡上進行二階鏈路預測任務效果并不好。

Table 2 AUC values of four networks表2 4個網(wǎng)絡中的AUC值

Table 3 Precision values of four networks表3 4個網(wǎng)絡中的Precision值

由表3 可知，將每對節(jié)點所得的計算指標做排序之后，各項基準指標均可以在候選目標節(jié)點集的前兩位中找到最優(yōu)節(jié)點，說明它們的預測性能較好。其中，4 項基準指標在Cora 網(wǎng)絡中均呈現(xiàn)出較高的精確率，因此可以推測本文的二階鏈路預測方法在Cora 這樣的大規(guī)模網(wǎng)絡結構中有不錯的表現(xiàn)。而Citeseer 網(wǎng)絡中的精確率較低，與表2中的AUC 結果不相符合，原因可能在于AUC 是從全局考察預測方法的性能，而Precision 是從幾條鏈接中檢驗預測精度，二者評價任務不一樣。綜合而言，該方法在Citeseer 網(wǎng)絡中的表現(xiàn)依然不錯。

為了進一步說明構建二階可達網(wǎng)絡以緩解數(shù)據(jù)稀疏性對本文所提方法的必要性，本文從所用數(shù)據(jù)集的網(wǎng)絡密度角度對各網(wǎng)絡上的表現(xiàn)進行比較分析。首先，一個包含N 個節(jié)點的網(wǎng)絡的密度ρ 是指網(wǎng)絡中實際存在的邊數(shù)M與最大可能的邊數(shù)之比。對于無向網(wǎng)絡，網(wǎng)絡的密度ρ有：

本文數(shù)據(jù)集所對應的網(wǎng)絡密度如表1 所示，可見稀疏度的關系表現(xiàn)為：Citeseer ＞ Cora ＞ Washington ＞ Texas，因此本文選擇在稀疏度上有所區(qū)分的前3 個網(wǎng)絡上根據(jù)AUC 指標值評估該方法的性能，實驗結果如圖3所示。

Fig.3 Changes of AUC value under different indicators圖3 不同指標下的AUC值變化

在各項基準指標下，稀疏度最大的網(wǎng)絡Citeseer 保持最優(yōu)的AUC 值，稀疏度中等的Cora 次之，稀疏度最小的Washington 網(wǎng)絡AUC 值最低。由此可見，網(wǎng)絡稀疏度越大，該方法的性能越好，因此本文所提出的方法相對適用于稀疏度較大的網(wǎng)絡。

為了探索訓練集比例對預測效果的影響以及各項指標的相對表現(xiàn)，本文在Cora 和Citeseer 網(wǎng)絡上作了進一步探究。圖4 給出了訓練集比例從0.4 增長到0.7 時，Cora 和Citeseer 網(wǎng)絡中基于不同基準鏈路預測指標的AUC 值變化。在Cora 網(wǎng)絡中，AUC 值初始呈上升趨勢，是因為訓練集比例增加能夠提供更多的訓練信息，從而提高了AUC值。隨著訓練集的增加，測試集會相應減少，當訓練集的比例增加到一定程度，在測試集中獲取鏈接的概率會降低，因而不易找到缺失的二階鏈路，故AUC 值會下降。在Citeseer 網(wǎng)絡中，AUC 值初始呈下降趨勢，是因為此時并沒有在訓練集中學到有用信息，而中間上升的值說明開始在訓練集中學到有效的訓練信息，并表現(xiàn)出來；之后，AUC 值表現(xiàn)出下降趨勢同樣是因為訓練集增加到一定程度，在測試集中獲取鏈接的可能性會減小。此外，網(wǎng)絡本身的結構特征（度數(shù)）在各項基準指標中占據(jù)著不一致的重要性，因此AUC 值在不同基準指標上的表現(xiàn)會有所差異。

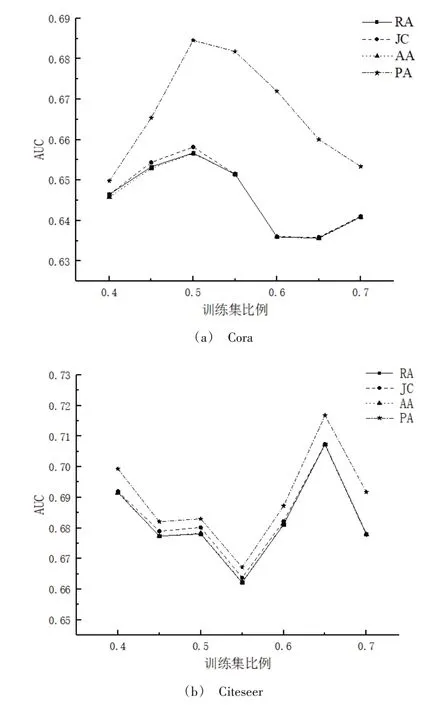
Fig.4 Changes of AUC value when ratio of training set increases from 40% to 70% in Cora and Citeseer network圖4 Cora和Citeseer網(wǎng)絡中訓練集比例由40%增加到70%時AUC的變化

4 結語

本文提出了基于節(jié)點相似性的二階鏈路預測方法，并構造了二階鏈路預測指標以識別節(jié)點對的中間節(jié)點，然后補全節(jié)點對之間的二階鏈路。該方法可以結合RA、JC、AA、PA 4 項相似性指標加以實現(xiàn)，為了驗證各指標性能及方法的有效性，分別在4 個真實的網(wǎng)絡數(shù)據(jù)上進行了實驗。結果表明，此方法在稀疏度較大的網(wǎng)絡上會表現(xiàn)出相對更好的性能，在AUC 和Precision 指標上表現(xiàn)良好，能夠精確地預測到所丟失的鏈路。下一步研究的重點是在基準預測指標上找到更加合適的搭配，比如基于節(jié)點的嵌入向量等，同時期待能夠在更普遍的網(wǎng)絡上發(fā)揮該方法的作用。