平臂式塔式起重機自振周期計算方法研究

韓志聰，郭兵，?，李加敖，石言民

(1.山東建筑大學土木工程學院，山東 濟南 250101；2.中建眾力設備租賃有限公司，山東 濟南 250202；3.山東建筑大學和平校區管理處，山東 濟南 250013)

0 引言

塔式起重機作為一種特種高危設備，安全狀況頻發，研究其動力特性對塔式起重機安全性能具有重要意義[1]。 閻玉芹等[2]指出對塔機的損傷監測可以及時發現塔機中存在的諸多安全隱患，增強塔機運行過程中的可靠性。 余震等[3]以某塔式起重機為研究對象，分析了常規工況下塔式起重機整體鋼結構應力情況及振動特性。 劉圣國[4]分析了塔機附著間距及懸臂高度等具體施工問題。 陳博文等[5]計算分析了雙肢剪力墻的自振，而牛文杰[6]研究了單樁風機的自振。 王帥等[7]利用有限元軟件ANSYS 研究了塔式起重機金屬結構的自振特性，通過模態分析獲取該結構的自振頻率及振型。 曹玉紅等[8]模態分析了塔式起重機；李俊儒[9]通過ANSYS軟件計算了塔式起重機自振周期。 由于格構式構件截面慣性矩計算起來較為復雜，孟麗霞[10]通過分析具有變截面臂架的格構式起重機結構，得到了塔身的等效慣性矩的計算方法，極大地方便了塔身簡化剛度的計算。

另外，我國有廣大地區處于地震帶上，為進一步了解地震激勵所帶來影響，了解塔式起重機動力特性，趙雪芹等[11]通過有限元軟件分析了平頭式塔式起重機，研究了其動態特性；付石等[12]分析了塔式起重機的動力學模態；鄭麗娟[13]研究了塔式起重機在風力及吊重下耦合作用；王平平等[14]對塔式起重機基于隨機振動理論進行了隨機地震激勵下的動態響應分析，數值仿真了塔式起重機在5 種不同組合方向輸入地震激勵時塔式起重機內力、位移的隨機地震響應。 王玲娟等[15]通過分析塔式起重機的風振響應，研究了塔式起重機在1 ～10 級風速工況下的諧響應曲線，得出了共振頻率和節點位移。

塔式起重機的自振周期是其基本屬性，關乎風振動力系數的選取，影響風載荷及其對塔身偏移的計算。 但是從上述文獻可以看出，目前純粹基于塔式起重機自振周期計算的研究仍然較少。 因此，文章以永茂5513 型塔帽式和中天6513 型平頭式塔式起重機為例，通過現場試驗與有限元軟件模態分析的自振周期對比，驗證了有限元建模方式的準確性，并對塔身進行剛度簡化，將塔式起重機簡化為單自由度模型，推導了自振周期簡化公式，對比分析了現場測試和有限元模擬結果，驗證了該公式的可行性。通過擴大有限元模擬的范圍，引入考慮塔機質量分布影響的修正系數，以期獲得精確并具有普遍適用性，以滿足工程實際需要的塔式起重機自振周期計算公式。

1 自振周期現場測試

1.1 自振周期測試方案

周期測試于濟南市槐蔭區的山東第一醫科大學在建工地現場進行，測試設備為中建眾力設備租賃有限公司提供的永茂5513 塔帽式塔式起重機和中天6513 平頭式塔式起重機，通過拾振器拾取數據。測試當天的風力微弱，現場風速＜2 m/s、風力等級為1 級。 為擴大數據采集范圍，對兩種型號塔式起重機進行多次加載，起吊重物從工地現場挑選，加載質量及工況見表1。

表1 兩種塔式起重機加載質量及工況表

1.2 測試結果及數據分析

考慮塔式起重機的外荷載(主要是風荷載)及自身慣性的影響，數據處理時選取均勻且平穩區段，每段周期數≥10 個，確保實測數據準確可靠。 塔式起重機的現場實測振動速度－時間曲線如圖1、2 所示，對已經得到結構的振動速度－時間曲線，通過快速傅里葉變換(Fast Fourier Transform， FFT)將時域信號轉換為頻域信號，其處理步驟為:(1) 獲取振動速度－時間曲線的離散樣本數據，確定樣本數據的長度為2 的冪次方，對不符合要求的數據，通過補零操作來擴展信號的長度，使其滿足條件；對時域信號應用窗函數，減少頻譜泄漏，提高頻譜分辨率。(2) 獲取FFT 結果的頻譜數據，應用FFT 算法，計算了窗函數處理后的樣本數據，將所得到的復數序列，通過計算每個復數的模(絕對值)獲取振幅譜。(3) 根據采樣頻率和FFT 結果的長度，計算頻率分辨率。 該分辨率表示頻率軸上相鄰兩個頻率點之間的間隔，對頻譜數據進行幅值歸一化，以便更好地顯示頻譜，可以將振幅譜除以最大振幅，使其范圍在0 ～1之間。 (4) 對頻域信號進行頻域處理，去除噪聲及突出特定頻率成分。

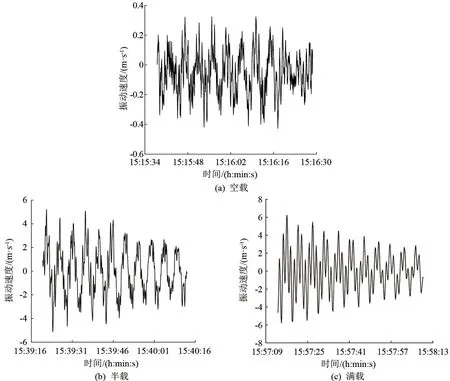
圖1 永茂5513型塔式起重機實測振動速度－時間曲線圖

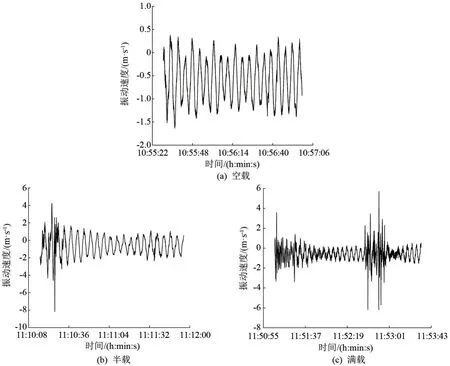
圖2 中天6513型塔式起重機實測振動速度－時間曲線圖

最后，得到永茂5513 和中天6513 兩種塔式起重機的現場實測自振周期數值，見表2。

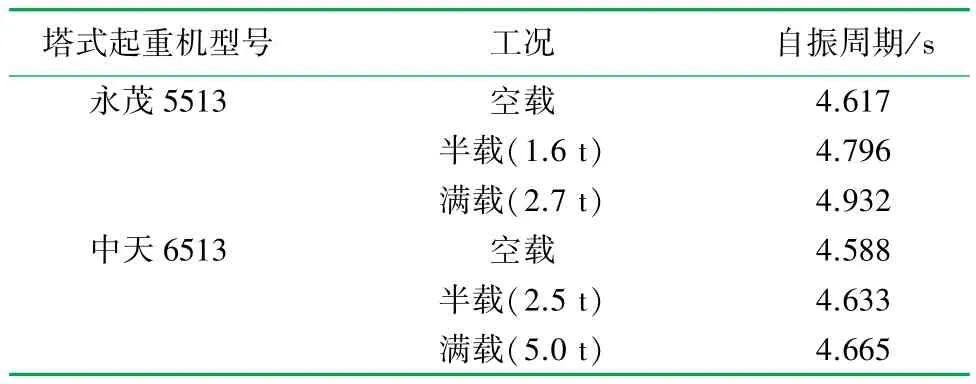
表2 兩種塔式起重機振動周期對比表

兩種型號的塔式起重機的自振周期隨起吊重物質量的增大而增大，符合結構力學的一般規律，且與永茂5513 型塔式起重機相比，中天6513 型塔式起重機的主肢截面尺寸較大，故其塔身整體剛度較大，同等質量條件下自振周期應相對較小。

2 有限元模擬和分析

塔式起重機有限元分析，以永茂5513 型和中天6513 型塔式起重機為例，采用有限元軟件ABAQUS分別建立數值模型，塔身尺寸均為1.6 m×1.6 m，塔身主肢、塔身水平腹桿、塔身斜腹桿、起重臂上的各個桿件以及平衡臂等選用線單元建模，以方便指派梁截面形式和尺寸；回轉平臺、起吊重物、平衡重選用實體單元，通過自定義材料密度來控制起吊荷載。由于塔帽質量較小，對永茂5513 型塔式起重機省略建模過程，將質量均勻加在起重臂上，而司機室重量加于回轉平臺上。

連接方式上，回轉平臺與塔身頂端之間、平衡重與平衡臂末端之間均采用綁定，塔身底端與地面使用完全固接約束。 為最大程度反映塔式起重機的實際振動情況，建立的有限元模型具體規格采用遼寧安全科學研究院通過的試驗報告中給出的實際尺寸。

永茂5513 和中天6513 兩種型號塔式起重機對應的有限元模擬與現場測試的自振周期對比見表3，對應的自振周期絕對誤差最大值分別為4.87%和4.29%，其值均＜5%。 考慮到無法準確模擬塔式起重機各個部分的連接，且塔帽、鋼絲繩、小車、司機室等次要結構建模時做了簡化計算，因此認為現有偏差在合理范圍內，建模方式貼合實際。

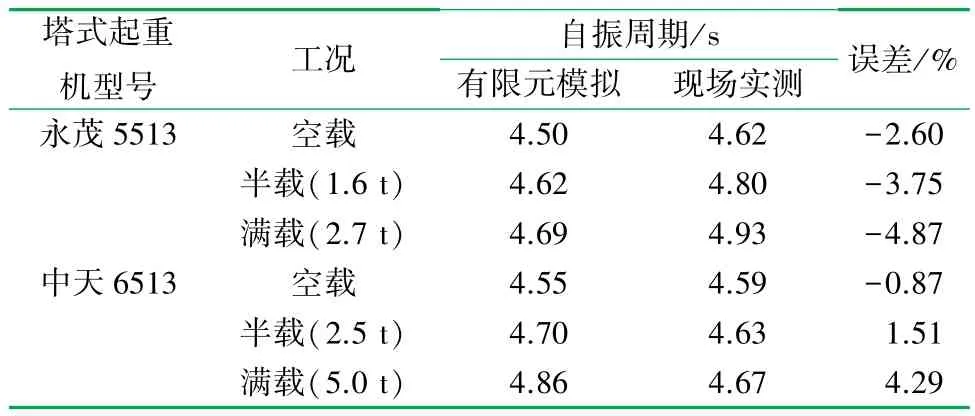
表3 塔式起重機有限元模擬與現場實測自振周期對比表

永茂5513 塔帽式、中天6513 平頭式塔式起重機有限元模型第一階模態位移云圖如圖3所示。

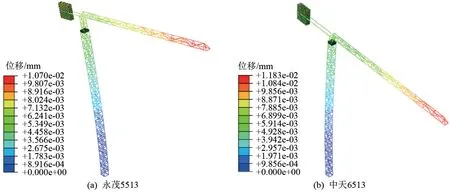
圖3 不同型號塔式起重機位移云圖

3 自振周期簡化計算公式推導及驗證分析

3.1 簡化計算公式推導

通過圖3 有限元模態分析的第一階振型位移云圖可知，塔式起重機的振動幅度隨著自身高度的增加而增大，塔身呈單向傾斜，屬于單曲率彎曲，其振動與單自由度構件類似，因此可將塔式起重機的計算模型簡化為一個單自由度結構體系，塔身截面(如圖4 所示)的慣性矩可按照格構式構件的等效慣性矩計算方法得到。 塔身截面的慣性矩由式(1)[2]表示為

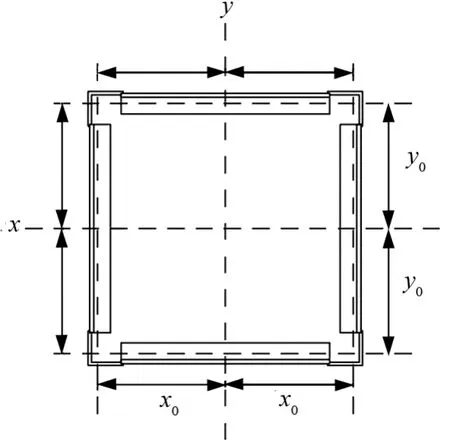
圖4 塔式起重機塔身截面示意圖

將塔式起重機總質量分為上、中、下3 個部分，其中上部質量包括回轉平臺以上的平衡重、起重臂及平衡臂等；中部質量為回轉平臺；下部質量為塔身。 把塔身看成只有剛度沒有質量的理想格構式構件，對上、下部質量在塔身頂端折中，即將塔式起重機3 個部分質量集中于一個位于塔身頂端的質點上。 以塔帽式塔式起重機為例，其簡化模型如圖5所示。

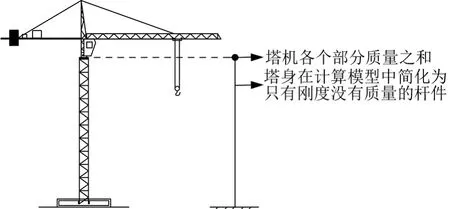
圖5 塔式起重機簡化模型圖

對于圖5 所示的塔式起重機簡化模型，結構力學單自由度體系通用的自振頻率的計算公式由式(2)表示為

將格構式桿件的慣性矩公式(1)用在塔身上，代入式(2)，得到塔式起重機自振頻率ω 的計算公式由式(3)表示為

式中l0為標準節邊長的一半，m。

格構式構件μ 取0.9[2]，則簡化后的塔式起重機自振周期T 計算公式由式(4)表示為

3.2 驗證分析

永茂5513 和中天6513 兩種型號的塔式起重機的主肢截面積、標準節邊長、獨立高度以及塔式起重機工作狀態下的重量等參數見表4。 根據式(4)，計算了表4 中兩種型號塔式起重機6 種工況下的自振周期，并結合表3 給出了簡化公式計算自振周期與實測值的誤差，見表5。 簡化公式計算的自振周期與現場實測值的絕對誤差最大值為9.59%，滿足工程要求。

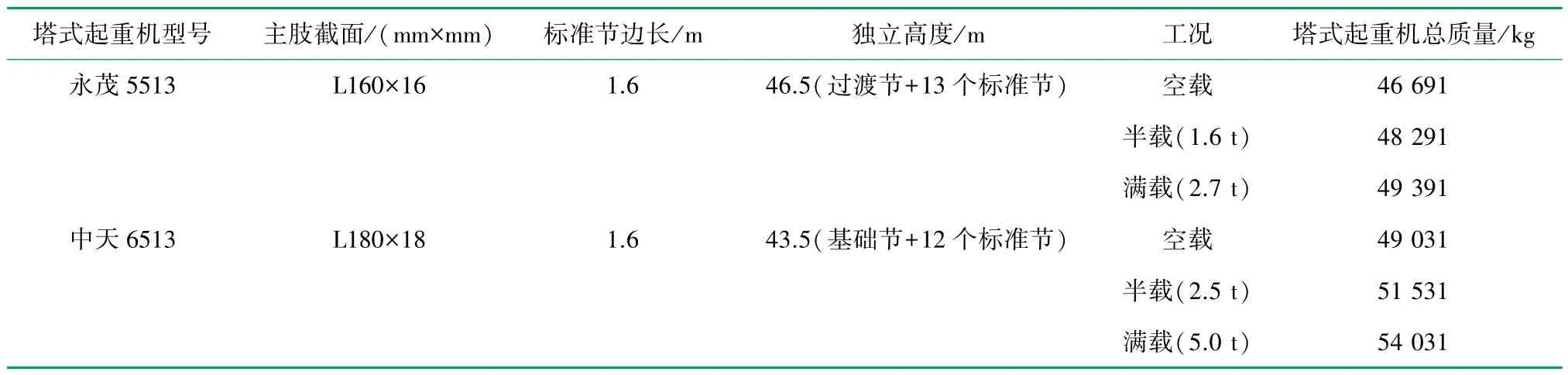
表4 塔式起重機參數表

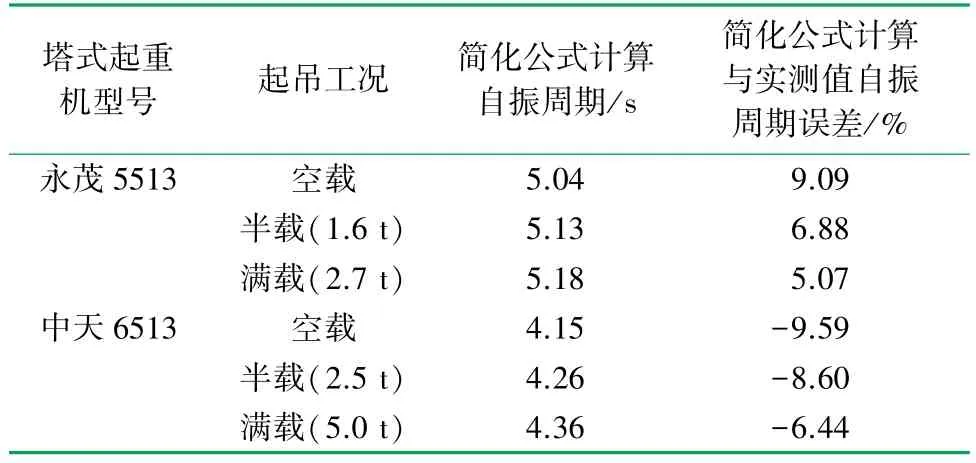
表5 簡化公式計算與實測自測周期誤差表

3.3 結果差異分析

兩種塔式起重機的空載質量相近，簡化公式計算完全按照單自由度構件推導得出，質心位置很大程度上影響了簡化模型剛度取值。 質心實際與塔身頂端并不完全重合，會因塔式起重機的質量分布不同而產生變化。 兩種型號塔式起重機常態質量分布的實際質心位置示意圖如圖6 所示。

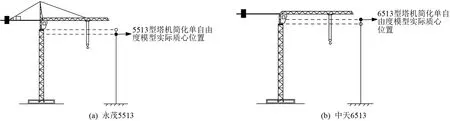
圖6 兩種型號塔式起重機常態質量分布實際質心位置示意圖

由表3、5 可知，對于5513 型塔式起重機，簡化計算公式計算的自振周期相比現場測試及有限元模擬結果均偏大，可以認為產生這種現象的原因是公式選取的質心位置計算高度較模型實際質心位置高，間接取小了理想格構式桿件的剛度(如圖6(a)所示)；同樣，對6513 型塔式起重機來說，計算得到自振周期結果較現場測試及有限元模擬結果均偏小，可理解為簡化的單自由度模型實際質心位置應比塔身頂端高(如圖6(b)所示)。 綜上所述，簡化計算公式計算的自振周期與現場提取周期、有限元模擬結果相比仍有差異，由于塔式起重機自振周期的數值對風荷載取值影響深遠，為實現精確計算，獲得更好的實用性，應修正簡化的計算公式。

4 簡化計算公式修正

由于塔式起重機上部結構中的起重臂與平衡臂、平衡重質量較大，為了保證修正公式具有普遍適用性，將上部結構占塔式起重機總質量比例的最低值取得盡可能小，其值定為0.3；塔身與回轉中心占有較大質量，決定了上部結構占比亦不會過大，為了保證修正公式的普遍適用性，現將上部結構占結構總質量比例的最大值取得盡可能大，文章定為0.7。故驗證測試數據的取值范圍介于0.3 ～0.7 之間，各新建模型塔身及回轉質量相同，按照塔式起重機上部結構占總體質量的不同比例，分別得到塔帽式和平頭式塔式起重機有限元模擬與簡化公式計算的自振周期，見表6、7，其中λ 為有限元模擬值與簡化計算公式計算值的比值。

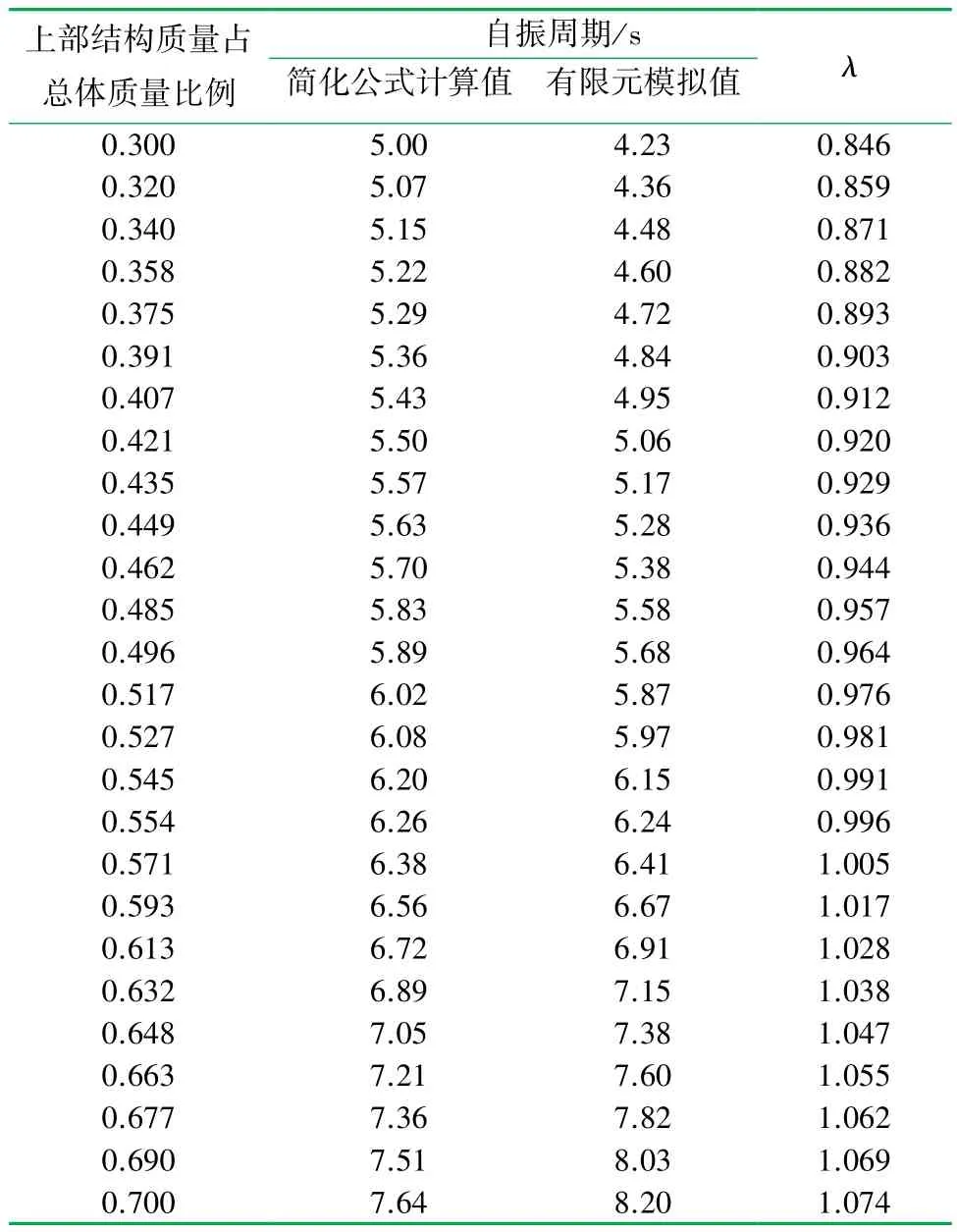
表6 不同上部質量對應塔帽式塔式起重機自振周期表

由于上部結構質量占比對質心位置影響深遠，將塔身頂端看作簡化單自由度模型時，質心位置應考慮實際塔身高度的影響。 為進一步得到精確計算結果，將比值λ看作修正系數。

考慮塔機質量分布影響的修正系數λ，修正式(4)后，得到的自振周期計算公式由式(5)表示為

對于塔帽式塔式起重機，λ ＝0.57＆＋0.68(＆為起重機上部結構質量占總質量比例)，λ 可以從表6中直接選取或者按照此公式線性內插得到；對于平頭式塔式起重機，λ ＝0.85＆ ＋0.67，λ 可以從表7 中直接選取或者按照此公式線性內插得到。

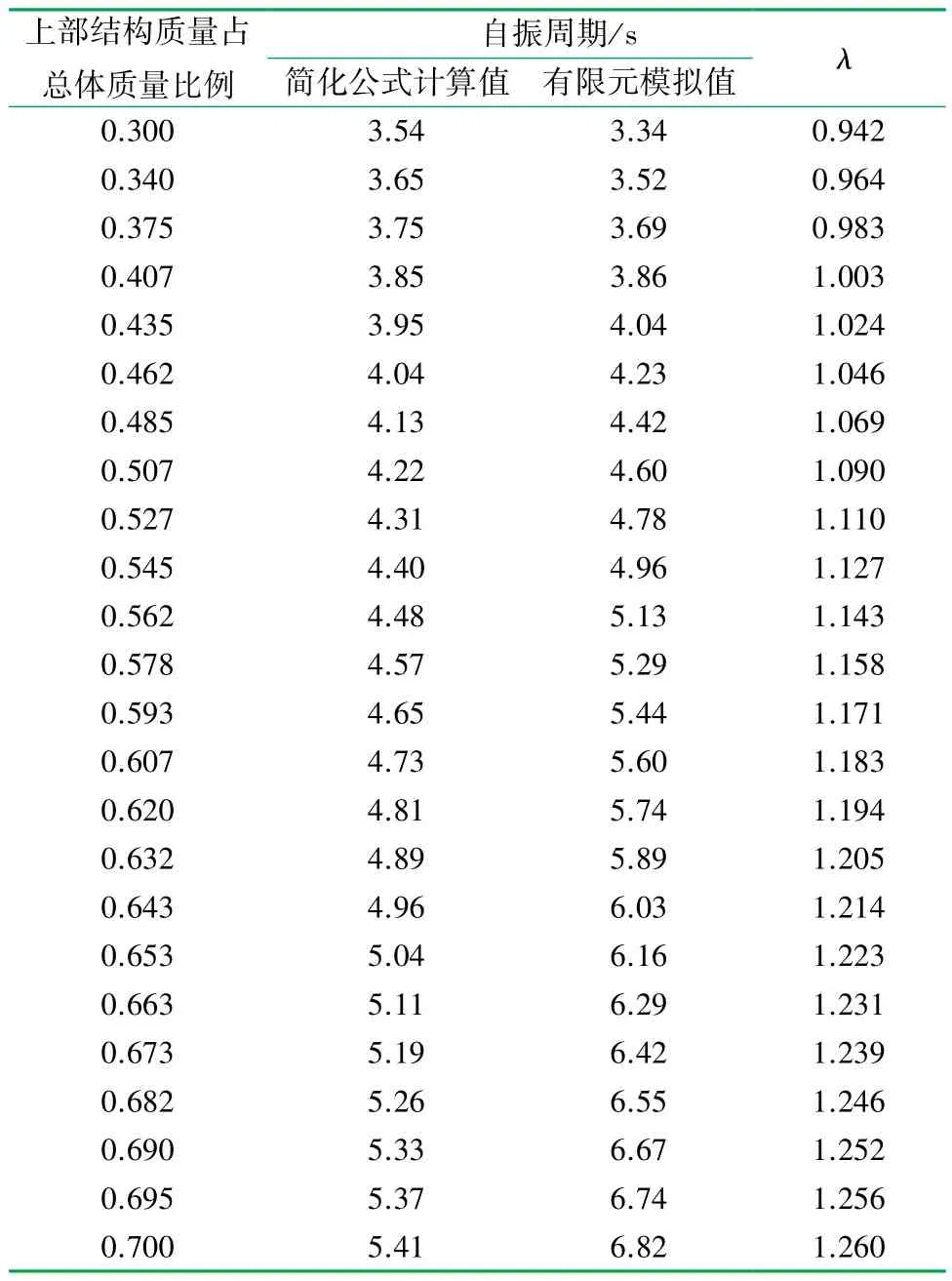
表7 不同上部質量對應平頭式塔式起重機自振周期表

5 結論

通過上述研究可知:

(1) 塔式起重機自振周期的簡化公式計算結果與現場實測結果吻合較好。 塔帽式塔式起重機、平頭式塔式起重機簡化公式計算的自振周期與現場實測值的絕對誤差最大值分別為9.09%和9.59%，在粗略計算塔式起重機自振周期時可以使用該簡化公式。

(2) 引入考慮塔機質量分布影響的修正系數，給出了塔式起重機自振周期簡化計算公式的修正公式，以契合多種塔機實際情況，并給出了塔帽式、平頭式塔式兩種起重機修正系數的推薦值及線性內插公式。