利用改進(jìn)的PnMl方法處理GRACE南北條帶誤差

1 數(shù)據(jù)和處理方法

1.1 數(shù) 據(jù)

本研究采用3大機構(gòu)(CSR、JPL、GFZ)2002-04～2019-09的GRACE/GFO 月時變重力場模型(即球諧系數(shù)模型)估計全球質(zhì)量場變化。將模型截斷至60階次并移除背景重力場(平均重力場),獲得月重力場變化量。球諧系數(shù)模型的一階項由GRACE/GFO數(shù)據(jù)結(jié)合海洋數(shù)值模型確定[5],C20和C30項由相應(yīng)的高精度衛(wèi)星激光測距結(jié)果替代[6-7],冰川均衡改正則采用ICE-6G_D模型[8]。此外,采用CSR發(fā)布的RL06版本GRACE/GFO 0.25°×0.25° Mascon產(chǎn)品(CSR-RL06M v02),記為CSR-M[9]。除橢球效應(yīng)外,CSR-M采用與球諧系數(shù)模型解相同的改正和替換。

1.2 利用球諧系數(shù)產(chǎn)品反演全球質(zhì)量場變化

以等效水柱高(EWH)表示的全球質(zhì)量場變化Δh可由GRACE/GFO 球諧系數(shù)模型計算[2]:

[ΔCnmcos(mλ)+ΔSnmsin(mλ)]

(1)

式中,θ、λ分別表示地心余緯與經(jīng)度;nmax為截斷階數(shù),在本文中為60;R為地球平均半徑;ρe和ρw分別表示地球平均密度和水密度;ΔCnm和ΔSnm為歸一化球諧系數(shù)變化量;Pnm為n階m次歸一化締合勒讓德多項式;kn為n階勒夫數(shù);Wnm為n階m次平滑核函數(shù)。

1.3 PnMl方法及其改進(jìn)方法

GRACE/GFO球諧系數(shù)模型在空間域具有明顯的南北條帶誤差[10]。研究表明[3],條帶誤差與球諧系數(shù)的次相關(guān)誤差模式有關(guān)。在以往研究中,為抑制該誤差,Chen等[4]將PnMl(P4M6)方法應(yīng)用于60階次截斷的GRACE球諧系數(shù)模型。

PnMl方法共有3個自由度,Nmin為球諧系數(shù)參與擬合部分的最低階數(shù),Nmax為球諧系數(shù)參與擬合部分的最高階數(shù),P表示用于擬合相關(guān)誤差的多項式次數(shù)。數(shù)學(xué)模型如下:

(2)

(3)

高次位系數(shù)的不足使全局保持?jǐn)M合次數(shù)為P的多項式在接近nmax時難以擬合,導(dǎo)致應(yīng)用60/96階次截斷(nmax=60/96)的GRACE/GFO時變重力場模型在經(jīng)PnMl方法處理后,大于50/86階次的位系數(shù)被完整保留(Nmax=50/86)[11]。未作處理的高階次位系數(shù)表現(xiàn)為殘余條帶,嚴(yán)重污染經(jīng)PnMl方法處理的反演結(jié)果。改進(jìn)方法仍保持PnMl方法的3個自由度及其基本思想,對PnMl方法未作處理的高次球諧系數(shù)(Nmax,Nmax+1,…,nmax)采取分層擬合。以P4M6方法為例,未經(jīng)改進(jìn)時多項式擬合次數(shù)P在全局保持不變(P=4),經(jīng)改進(jìn)后多項式擬合次數(shù)P在不同層次的計算公式為:

(4)

式中,Nmin為PnMl方法中位系數(shù)參與擬合部分的最低階數(shù),Nmax為PnMl方法中位系數(shù)參與擬合部分的最高階數(shù),nmax為截斷階數(shù)。p表示未經(jīng)改進(jìn)時在全局保持不變的多項式擬合次數(shù),在改進(jìn)方法中p=4。

1.4 信噪比評估

采用海陸均方根之比定義信噪比指標(biāo)[12],計算公式為:

(5)

1.5 基于廣義三角帽的不確定性評估

廣義三角帽方法假設(shè)不同觀測序列包含相同的真實信號和相互獨立的噪聲。對任意給定格網(wǎng)點或區(qū)域,設(shè)Xi(t)(i=1,2,3)為三大機構(gòu)GRACE/GFO時變重力場模型計算的陸地水儲量變化時間序列,如

(6)

式中,Y(t)為真實地球質(zhì)量變化信號,σi(t)為不同觀測序列的獨立噪聲。進(jìn)一步假設(shè)任意兩個獨立隨機的觀測值序列之和的方差等于兩者方差之和,構(gòu)造方差方程:

(7)

若觀測值序列中可用觀測值個數(shù)為n,展開式(7)可得n(n-1)/2個方差方程。由于方差方程個數(shù)大于或等于觀測數(shù),每個觀測值的噪聲方差可以直接求解,或在n>3時通過最大平方求解。

2 結(jié)果與分析

2.1 空域分析

以常用的P4M6方法為例,隨機選取2007-11和2019-09的CSR模型進(jìn)行測試,得到0.25°×0.25°全球質(zhì)量變化(以EWH表示)(圖1),圖中Gauss200表示半徑為200 km的高斯濾波。原始時變重力場中存在顯著的南北條帶誤差,經(jīng)P4M6方法處理后反演結(jié)果有所改善(圖1(a)、(d)、(g)),但低緯度區(qū)域(30°S～30°N)仍存在殘余條帶。而改進(jìn)方法可進(jìn)一步有效抑制殘余條帶誤差,即P4M6方法無法處理的高頻分量中的噪聲(圖1(b)、(h))。由差異圖可知,改進(jìn)方法可集中處理低緯度區(qū)域的條帶誤差(圖1(c)、(i))。對比傳統(tǒng)方法可知,改進(jìn)方法結(jié)合半徑為200 km的高斯濾波可使反演結(jié)果更加清晰(圖1(e)、(f))。殘余條帶的減少使后續(xù)處理只需應(yīng)用更弱的濾波策略便可得到清晰的反演結(jié)果,使?jié)撛诘牡厍蛭锢硇盘柕靡员槐Ａ艉徒沂尽?/p>

2.2 頻域分析

為分析改進(jìn)方法在頻域的性能,采用2007-11的CSR模型計算60階次球諧系數(shù)階方差(圖2(a)),并給出不同處理方案的振幅及其差異(圖2(b)～(e))。原始高階球諧系數(shù)的振幅出現(xiàn)較大異常值(圖2(b)),導(dǎo)致從25階開始,原始階方差呈現(xiàn)異常抬升變化(圖2(a))。經(jīng)P4M6方法處理后階方差的異常變化被抑制(圖2(c)),但較大的高階信號階方差會導(dǎo)致殘余條帶誤差。而改進(jìn)方法在50階后的階方差較P4M6方法有所下降,可去除高階突變值(圖2(d)、(e))。

圖2 60階次球諧系數(shù)階方差和在不同處理策略下的振幅

2.3 時域分析

在空域和頻域中,改進(jìn)方法已被證明優(yōu)于P4M6方法。為進(jìn)一步比較2種方法在時域的性能,在全球范圍內(nèi)選取4個經(jīng)典區(qū)域(3°×3°矩形質(zhì)量塊),矩形中心的大地坐標(biāo)分別為(44.5°E,21.5°S)、(32.5°E,0.5°S)、(85.5°W,12.5°N)、(0°E,7.5°N),分別位于馬達(dá)加斯加西南部、非洲維多利亞湖西北部、尼加拉瓜西北部、非洲沃特湖北部。

按式(1)計算得到矩形區(qū)域平均質(zhì)量變化時間序列,并加入CSR-M作為可靠數(shù)據(jù)源計算矩形區(qū)域質(zhì)量變化時間序列(圖3)。原始時間序列中的不合理峰值在采用P4M6方法后被部分移除,但仍存在殘余突變值。而改進(jìn)方法可進(jìn)一步減少時間序列中的孤立異常值,使信號更符合季節(jié)性變化,且與CSR-M計算結(jié)果具有較好的一致性。

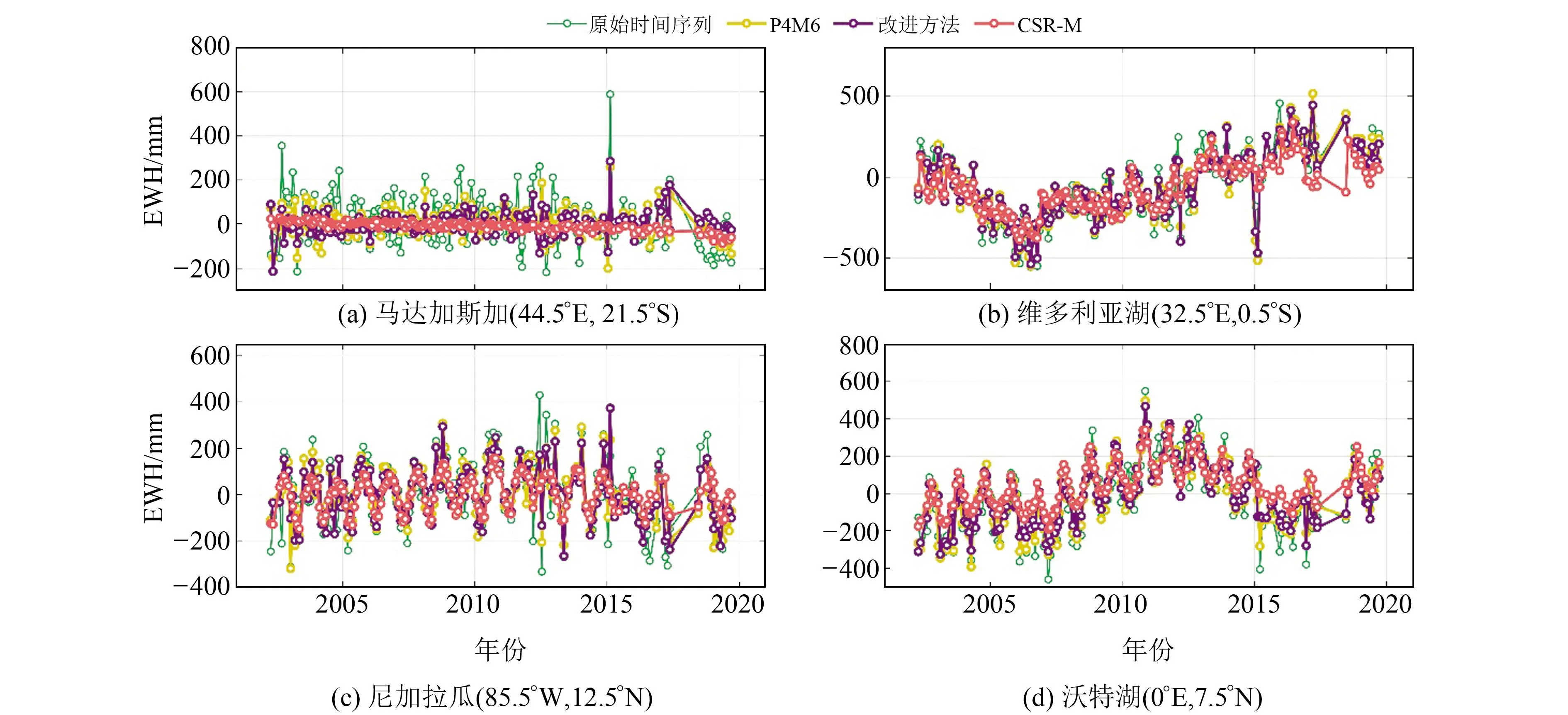
圖3 3°×3°矩形區(qū)域質(zhì)量變化時間序列

2.4 精度評定

改進(jìn)方法在空域、頻域和時域的性能提升已被證明。為了量化改進(jìn)方法去條帶誤差的效果,采用廣義TCH計算三大機構(gòu)模型以標(biāo)準(zhǔn)差(STD)表示的1°×1°全球不確定性格網(wǎng)評估改進(jìn)方法,統(tǒng)計3組處理結(jié)果在全球及4個矩形區(qū)域的平均STD并計算SNR(圖4)。

圖4 不同機構(gòu)模型精度統(tǒng)計

3種模型在采用改進(jìn)方法后,全球及4個矩形區(qū)域的平均STD較P4M6方法均有所改善。在全球范圍內(nèi),CSR、GFZ、JPL三種模型的平均STD分別下降20.50 mm、36.40 mm、19.61 mm(圖4(a)),表明改進(jìn)方法可以進(jìn)一步降低時變重力場模型的不確定性。此外,三者的SNR在采用改進(jìn)方法后較P4M6方法分別從1.62、1.19、1.25增加到1.77、1.35、1.39(圖4(b))。

3 結(jié) 語

為處理GRACE/GFO時變重力場模型的條帶噪聲,本文提出一種改進(jìn)的PnMl方法。該方法通過處理PnMl方法忽略的高次球諧系數(shù),進(jìn)一步抑制條帶噪聲。對比分析改進(jìn)方法與常用的P4M6方法在空域、頻域和時域的反演結(jié)果,同時采用廣義TCH和SNR指標(biāo)對該方法進(jìn)行精度評定。主要結(jié)論如下:

1)在空域中,改進(jìn)方法可進(jìn)一步抑制30°S～30°N區(qū)域的殘余條帶誤差,使反演結(jié)果更加清晰。

2)在頻域中,改進(jìn)方法可進(jìn)一步抑制50階后信號階方差的異常抬升,減少高階系數(shù)的階方差突變值。

3)在時域中,改進(jìn)方法可進(jìn)一步減少時間序列突變值,使信號更符合季節(jié)性變化。

4)經(jīng)統(tǒng)計,改進(jìn)方法的SNR、全球和局部區(qū)域的平均STD均有明顯改善。其中,CSR、GFZ、JPL三種模型結(jié)果在全球范圍的平均STD分別下降20.50 mm、36.40 mm和19.61 mm,SNR從1.62、1.19、1.25增加至1.77、1.35、1.39。這表明,改進(jìn)方法可通過進(jìn)一步抑制條帶誤差來降低反演結(jié)果的不確定性。