一種改進(jìn)的變權(quán)科莫多優(yōu)化算法及其應(yīng)用

梁少華，李林軒，葉青

長江大學(xué)計(jì)算機(jī)科學(xué)學(xué)院，湖北 荊州 434023

自然一直是許多元啟發(fā)式算法的靈感來源，如進(jìn)化論中的自然選擇是遺傳算法[1](genetic algorithm,GA)靈感來源，鳥群覓食過程是粒子群算法[2](particle swarm optimization,PSO)靈感來源等。智能算法已經(jīng)成功地解決各個領(lǐng)域的問題，包括旅行商問題[3]、最優(yōu)控制理論[4]、醫(yī)學(xué)圖像處理技術(shù)[5]等。為解決更加棘手的問題，相關(guān)學(xué)者相繼提出鷹棲息算法[6](eagle perching optimization,EPO)、灰狼算法[7](grey wolf optimization,GWO)、科莫多算法[8](komodo mlipir mlgorithm,KMA)以及各種改進(jìn)算法和方法，如加入PSO的混合鷹棲息算法[9]、混沌理論[10]、萊維(Levy)飛行[11-12]和動態(tài)權(quán)值[13]等方法應(yīng)用于智能算法中。

KMA是2022年1月由SUYANTO等提出的新穎的元啟發(fā)優(yōu)化算法，該算法有著遺傳算法和粒子群優(yōu)化算法的諸多優(yōu)點(diǎn)，可以通過不同階級個體的運(yùn)動和繁殖尋找最優(yōu)值，還提出通過種群自適應(yīng)[14]來控制局部和全局尋優(yōu)的平衡，使得KMA收斂速度較快和精度較高，并且在高維函數(shù)中具有延展性。但是KMA在復(fù)雜函數(shù)中仍存在局部收斂的問題。

為了進(jìn)一步提高KMA的性能，改進(jìn)KMA在收斂過程中存在的問題，筆者提出了一種改進(jìn)的變權(quán)科莫多優(yōu)化算法(VWCKMA)。主要創(chuàng)新和意義如下：①引入可變慣性權(quán)重因子[15]，將科莫多巨蜥的社會階級都賦予一個隨著迭代次數(shù)而改變的慣性權(quán)重，提升了種群的收斂速度和全局探索的能力；②引入了Tent混沌映射[16]初始化科莫多種群，提高初始化種群位置的質(zhì)量，豐富了種群的多樣性，提高了收斂速度；③利用Tent混沌映射[17]有效調(diào)節(jié)種群的多樣性，幫助算法動態(tài)跳出局部最優(yōu)，提高了收斂精度。

1 科莫多算法

在KMA中，隨機(jī)生成科莫多種群，根據(jù)適應(yīng)度劃分種群為3種不同的社會階級。通過3種階級的不同運(yùn)動，完成最后尋優(yōu)的過程。其中大型雄性的運(yùn)動行為用數(shù)學(xué)模型描述如下：

(1)

(2)

小型雄性的運(yùn)動通過特定的概率隨機(jī)選擇一部分去靠近大型雄性，用數(shù)學(xué)模型描述如下：

(3)

(4)

2 改進(jìn)科莫多算法以及算法流程

2.1 Tent混沌映射初始化粒子位置

目前大多數(shù)算法采用隨機(jī)初始化粒子的方式來表示，但是這容易造成個體集中在某一區(qū)域，分布不均衡。混沌序列具有內(nèi)在隨機(jī)性和空間遍歷性，能夠在一定的空間范圍內(nèi)不重復(fù)的無規(guī)律遍歷，能有效地避免局部最優(yōu)解，實(shí)現(xiàn)全局優(yōu)化。李兵等[18]將混沌理論應(yīng)用于群智能算法的優(yōu)化中，發(fā)現(xiàn)其優(yōu)化效率高于一般隨機(jī)算法。

Tent混沌映射具有簡單的結(jié)構(gòu)，同時迭代過程更加適合計(jì)算機(jī)的運(yùn)行，并且Tent混沌映射的遍歷性更加均勻。單梁等[16]表明了Tent混沌映射的遍歷性要比logistic混沌映射[19]更好，因此，采用Tent混沌映射對種群進(jìn)行初始化，式(5)是Tent混沌映射，其數(shù)學(xué)表達(dá)式為：

(5)

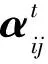
2.2 新增慣性權(quán)重策略及雌性運(yùn)動

為了避免KMA在搜索過程中陷入局部最優(yōu)值，在KMA中引入了一種新的參數(shù)稱為慣性權(quán)重，用于控制全局探索和局部搜索。對于大型雄性、雌性、小型雄性的運(yùn)動分別引入不同的慣性權(quán)重w1、w2、w3，所有的權(quán)重都應(yīng)該是變化的，并且相加時和為1。即：

w1+w2+w3=1

(6)

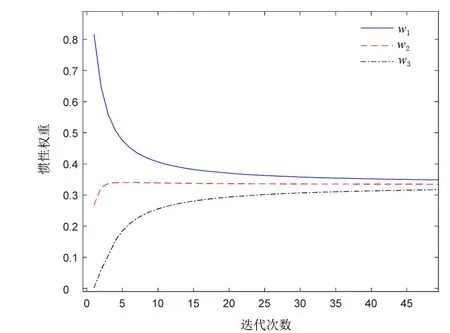
圖1 可變權(quán)值的迭代圖Fig.1 Iterative graph of time-varying weights

(7)

(8)

基于以上這些假設(shè)和因素，提出了一種新的可變慣性權(quán)重更新方法，定義為：

w1=cosθ

w3=1-w1-w2

(9)

可變慣性權(quán)重曲線如圖1所示。

將大型雄性運(yùn)動的數(shù)學(xué)表達(dá)式(1)改進(jìn)為：

(10)

KMA中雌性只存在有性繁殖或者無性繁殖的行為，根據(jù)自然界正常生理活動，新增雌性向大型雄性移動的新運(yùn)動，其運(yùn)動的數(shù)學(xué)表達(dá)式為：

(11)

最后，同樣對小型雄性的運(yùn)動增加慣性權(quán)重w3，即對式(3)進(jìn)行改進(jìn)。則其數(shù)學(xué)表達(dá)式為：

(12)

2.3 新增Tent混沌映射擾動策略

在完成科莫多3種階級運(yùn)動后，進(jìn)行混沌擾動實(shí)現(xiàn)局部搜索。使用Tent混沌映射進(jìn)行擾動，在科莫多個體周圍產(chǎn)生一些局部解，然后再與之前的最優(yōu)解進(jìn)行比較。具體的Tent混沌映射擾動步驟如下：

2.4 VWCKMA整體流程

VWCKMA的具體算法流程如圖2所示。

步驟1 初始化參數(shù)，初始化種群和維度大小，最小和最大的自適應(yīng)種群規(guī)模的大小，最大迭代次數(shù)，最大混沌次數(shù)，大型雄性的個數(shù)；

步驟2 初始化種群，利用Tent混沌映射初始化科莫多個體群的位置；

步驟3 計(jì)算科莫多個體的適應(yīng)度值，利用式(6)～式(9)計(jì)算不同社會階級科莫多的慣性權(quán)值；

步驟4 更新位置，根據(jù)式(2)和式(10)更新大型雄性的位置，式(11)更新雌性的位置，式(4)和式(12)更新小型雄性的位置；

步驟5 使用式(5)進(jìn)行Tent混沌映射擾動，進(jìn)行局部搜索。

步驟6 判斷是否得到最優(yōu)解或達(dá)到最大的迭代次數(shù)，如果是算法搜索結(jié)束執(zhí)行步驟7；否則返回到步驟3；

步驟7 輸出最優(yōu)值信息。

圖2 VWCKMA的執(zhí)行框架Fig.2 Implementation framework of VWCKMA

2.5 改進(jìn)算法復(fù)雜度分析

KMA的時間復(fù)雜度為O(n×m×Max_iteration+f(n)+α1)(其中n，m，f(n)，α1和Max_iteration分別代表種群中個體的數(shù)量，維度，目標(biāo)函數(shù)計(jì)算時間，適應(yīng)度值排序過程的時間和最大迭代次數(shù))VWCKMA時間復(fù)雜度分析如下：

1)Tent混沌映射初始化種群的時間復(fù)雜化為O(n×m)，則引入Tent混沌映射初始化種群的算法時間復(fù)雜度為O(n×m×Max_iteration+f(n)+α1+n×m)=O(n×m×Max_iteration+f(n)+α1)。 2)假設(shè)更新時變慣性權(quán)重的所需時間為t1，引入時變慣性權(quán)重后算法的時間復(fù)雜度為O(n×m×Max_iteration+f(n)+α1+t1)=O(n×m×Max_iteration+f(n)+α1)。

3)Tent混沌映射進(jìn)行擾動的時間復(fù)雜度為O(n×m)，引用Tent混沌映射進(jìn)行擾動的算法時間復(fù)雜度為O(n×m×Max_iteration+f(n)+α1+n×m)=O(n×m×Max_iteration+f(n)+α1)。

VWCKMA空間復(fù)雜度分析如下：加入Tent混沌映射初始化種群和慣性權(quán)重的優(yōu)化策略均在KMA基礎(chǔ)上改進(jìn)，未新增存儲空間。加入Tent混沌映射擾動策略后新增的空間復(fù)雜度為O(logk)(其中k為最大混沌次數(shù))。與KMA相比略微增加了O(logk)，但是在現(xiàn)有計(jì)算機(jī)硬件水平中O(1)≈O(logk)。

綜上所述，相比KMA，筆者提出的VWCKMA沒有增加復(fù)雜度。

3 仿真實(shí)驗(yàn)及分析

3.1 測試函數(shù)集

為了綜合檢驗(yàn)VWCKMA具有效性和優(yōu)越性，將VWCKMA同時與KMA，GWO算法和PSO算法對8個基準(zhǔn)函數(shù)進(jìn)行求解，單峰函數(shù)f1(x)～f3(x)，多峰函數(shù)f4(x)～f8(x)，函數(shù)信息如表1所示。

表1 基準(zhǔn)函數(shù)

3.2 實(shí)驗(yàn)數(shù)據(jù)及分析

參數(shù)設(shè)置相同，VWCKMA與KMA，GWO和PSO算法的迭代次數(shù)為200次，最大種群規(guī)模為200。在該條件下對30維度、100維度和500維度的8個基準(zhǔn)函數(shù)獨(dú)立運(yùn)行30次，進(jìn)行尋優(yōu)計(jì)算。計(jì)算出各個算法的均值和標(biāo)準(zhǔn)差(見表2)。其中最優(yōu)者用黑體加下劃線標(biāo)注。為了更加直觀地體現(xiàn)VWCKMA的優(yōu)越性能，在30維度的測試函數(shù)中，繪制出部分測試基準(zhǔn)函數(shù)的收斂曲線圖，如圖3所示。所涉代碼采用MATLAB R2020a軟件編寫，仿真實(shí)驗(yàn)環(huán)境為：64位Windows操作系統(tǒng)，CPU型號為Intel Core i7-12700 F，機(jī)帶RAM為32 GB。

表2 4種算法在8個基準(zhǔn)函數(shù)上的測試結(jié)果

圖3 基準(zhǔn)函數(shù)的收斂曲線Fig.3 Convergence curve of benchmark functions

在同維度和迭代次數(shù)的情況下，表2的結(jié)果表明：VWCKMA在單峰函數(shù)f1(x)～f3(x)中能收斂到函數(shù)的理論最優(yōu)值，其他算法都無法收斂到0。VWCKMA在多峰函數(shù)中，f4(x)～f6(x)函數(shù)均表現(xiàn)出收斂到函數(shù)理論最優(yōu)值，在f7(x)和f8(x)函數(shù)中收斂精度最高。對比結(jié)果說明VWCKMA的精度高于KMA、GWO算法和PSO算法。對比500維度情況，f1(x)～f6(x)函數(shù)均收斂到函數(shù)理論最優(yōu)值，f7(x)和f8(x)函數(shù)收斂精度仍最高，表明VWCKMA在高維情況下仍具有收斂的精準(zhǔn)性。圖3表明：VWCKMA在f4(x)～f7(x)函數(shù)中平均迭代5次便能夠快速準(zhǔn)確地收斂到最佳值，在f7(x)函數(shù)中KMA陷入局部最優(yōu)值時VWCKMA能有效跳出局部最優(yōu)值。無論從收斂精度還是速度上都遠(yuǎn)遠(yuǎn)高于PSO，GWO和KMA。說明該算法較其他3種元啟發(fā)算法具有收斂精度更高、速度更快的突出優(yōu)勢。

綜上分析所得，VWCKMA與PSO、GWO和KMA比較，無論是在低維度還是高維度，無論在收斂精度還是收斂速度方面，無論是在單峰函數(shù)還是多峰函數(shù)情況下的尋優(yōu)計(jì)算，VWCKMA都具有明顯的優(yōu)勢。同時VWCKMA有較強(qiáng)的全局探索與局部搜索的能力和較快的收斂速度，且對于局部最優(yōu)解有很強(qiáng)的抵抗性，能夠輕易地跳出局部最優(yōu)解，找到函數(shù)的最優(yōu)值。

4 應(yīng)用

4.1 對象與方法

將VWCKMA應(yīng)用在成都市空氣污染物PM2.5預(yù)測的實(shí)際問題中。通過MATLAB進(jìn)行仿真實(shí)驗(yàn)，選擇傳統(tǒng)的BP神經(jīng)網(wǎng)絡(luò)[20]、粒子群優(yōu)化神經(jīng)網(wǎng)絡(luò)[21](PSO-BP)、科莫多優(yōu)化神經(jīng)網(wǎng)絡(luò)(KMA-BP)，以及改進(jìn)科莫多優(yōu)化神經(jīng)網(wǎng)絡(luò)(VWCKMA-BP)4種模型分別對成都市空氣污染物PM2.5進(jìn)行預(yù)測。為了公平性，4種預(yù)測模型的參數(shù)設(shè)定一致，參數(shù)設(shè)定如下：BP神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu)為5-10-5-1，輸入層到隱藏層之間的傳遞函數(shù)為Tansig函數(shù)，隱藏層到輸出層之間的傳遞函數(shù)為Poslin函數(shù)，學(xué)習(xí)率設(shè)置為0.4。樣本數(shù)據(jù)的選取來自于中國空氣質(zhì)量在線監(jiān)測分析平臺(https：//www.aqistudy.cn)，選取成都市2020年1月1日至2022年6月30日一共912條數(shù)據(jù)進(jìn)行實(shí)驗(yàn)。具體數(shù)據(jù)包括日期、AQI、質(zhì)量等級、PM2.5、PM10、CO、NO2、SO2、O3。數(shù)據(jù)簡況見表3，由于篇幅有限列舉一部分?jǐn)?shù)據(jù)。

評價指標(biāo)在選取PM2.5的實(shí)際值和真實(shí)值的比較基礎(chǔ)上，再引入了平均相對誤差(EMR)，平均相對誤差均方誤差EMS，平均絕對誤差EMA，均方根誤差ERMS和預(yù)測準(zhǔn)確率Pacc進(jìn)行全方位的比較預(yù)測精度。預(yù)測模型都采用均方誤差函數(shù)作為算法的適應(yīng)度函數(shù)，5個指標(biāo)的數(shù)學(xué)定義分為：

(16)

(17)

(18)

(19)

(20)

表3 原始數(shù)據(jù)樣本

4.2 結(jié)果分析

在2020年1月1日至2022年6月30日的912條數(shù)據(jù)中選擇70%為訓(xùn)練集，30%為測試集。4種預(yù)測模型的預(yù)測值與真實(shí)值的對比結(jié)果如圖4所示。VWCKMA-BP模型的預(yù)測值與真實(shí)值的比較結(jié)果如圖5所示。從圖5可清晰看出，VWCKMA-BP模型更加接近真實(shí)值，通過VWCKMA使得尋優(yōu)精度得到有效提升。

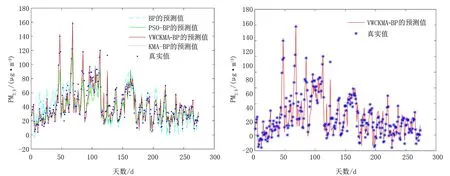
圖4 PM2.5的預(yù)測值和真實(shí)值對比圖5 VWCKMA-BP的預(yù)測值和真實(shí)值對比Fig.4 Comparison of predicted and true Fig.5 Comparison of predicted and true values PM2.5 values of VWCKMA-BP

表4為4種預(yù)測模型在測試集上的EMR、EMS、EMA、ERMS和Pacc這5個指標(biāo)的統(tǒng)計(jì)結(jié)果。從表4中可以看出不同優(yōu)化策略對BP神經(jīng)網(wǎng)絡(luò)的預(yù)測有較大的影響，VWCKMA-BP模型準(zhǔn)確率達(dá)到85.085%。4種模型只有VWCKMA-BP模型使得平均絕對誤差低于6 μg/m3，均方根誤差低于60 μg/m3，均方誤差低于15%。改進(jìn)算法在迭代次數(shù)上也有進(jìn)一步的提升，KMA、PSO和VWCKMA的對比收斂曲線如圖6所示，VWCKMA的初始適應(yīng)度值均優(yōu)于其他兩種算法，這是Tent混沌映射初始化種群的結(jié)果。在迭代30次左右時，VWCKMA的函數(shù)適應(yīng)度接近收斂值，其他算法適應(yīng)度值均大于VWCKMA。以上結(jié)果表明VWCKMA-BP模型在預(yù)測空氣污染物PM2.5指標(biāo)上有效可行。

表4 不同模型的指標(biāo)統(tǒng)計(jì)結(jié)果對比

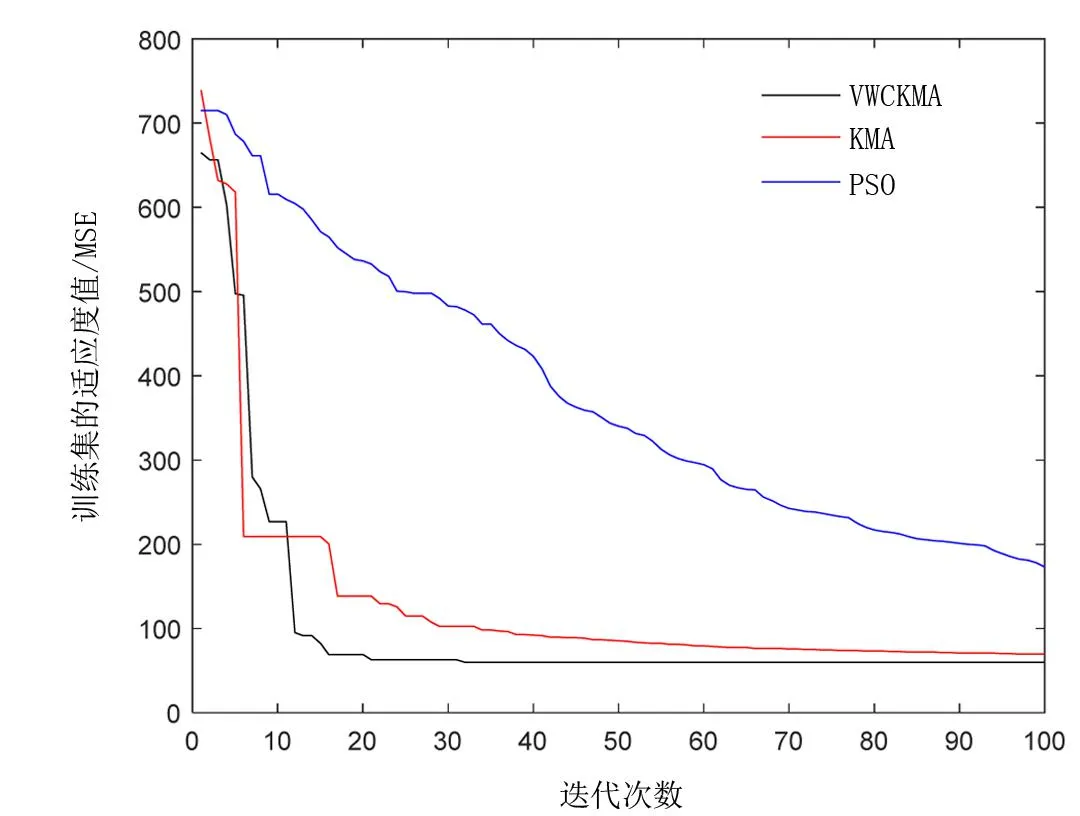
圖6 不同算法迭代收斂曲線對比Fig.6 Comparison of iterative convergence curves of different algorithms

5 結(jié)論

1)為進(jìn)一步提高KMA性能，改進(jìn)KMA在收斂過程中存在的問題，筆者提出根據(jù)隨迭代次數(shù)變化的慣性權(quán)值策略，提高收斂速度；利用Tent混沌映射初始化種群，保證種群多樣性，提高收斂速度；針對KMA易陷入局部最優(yōu)解的問題，采用Tent混沌映射能夠有效跳出局部最優(yōu)解，更加精確地對最優(yōu)解進(jìn)行搜索。

2)在仿真實(shí)驗(yàn)中，將VWCKMA與PSO、GWO、KMA進(jìn)行比較，選擇了8個不同性質(zhì)的基準(zhǔn)函數(shù)進(jìn)行函數(shù)優(yōu)化的實(shí)驗(yàn)。實(shí)驗(yàn)表明VWCKMA在函數(shù)尋優(yōu)的收斂精度與速度方面具有突出優(yōu)勢。

3)在實(shí)際應(yīng)用中，使用VWCKMA-BP、PSO-BP、KMA-BP和BP神經(jīng)網(wǎng)絡(luò)進(jìn)行空氣污染物PM2.5的實(shí)際預(yù)測，實(shí)驗(yàn)表明VWCKMA-BP模型預(yù)測準(zhǔn)確率在4種模型中最高，達(dá)到85.085%，相比BP神經(jīng)網(wǎng)絡(luò)預(yù)測準(zhǔn)確率提高19.85個百分點(diǎn)。說明VWCKMA在函數(shù)優(yōu)化以及實(shí)際優(yōu)化問題方面的性能得到了顯著提高。后續(xù)可將VWCKMA嘗試應(yīng)用于多目標(biāo)優(yōu)化解析中。