并網光伏發電機組中旋轉機械驅動控制方法研究

劉 偉

（新疆天富集團有限責任公司，石河子 832000）

并網光伏發電機組作為一個規模超大的并網發電系統，主要作用是將光伏陣列裝置接收到的太陽能輻射轉化為高電壓直流電，并經過逆變器的反向轉化后將電壓同頻同相的正弦型交流電流輸入到電力系統中。但其在戶外環境中易受到強風、暴雨、沙塵等因素影響，引發旋轉機械的動不平衡問題。為了提高并網光伏發電機組的工作效率，保障其安全穩定運行，相關專家學者對并網光伏發電機組旋轉機械驅動控制方法展開了深入研究[1-2]。

本文針對并網光伏發電機組旋轉機械提出一種新的驅動控制方法。為了準確評估旋轉機械的運行狀態和性能，計算并網光伏發電機組暫態響應和旋轉機械動不平衡量，得到發電機組在自然坐標系、原始坐標系以及旋轉坐標系下的不同運動狀態，將虛擬同步發電機（virtual synchronous generator，VSG）本體算法和VSG 控制策略結合在一起，構建基于VSG 的旋轉機械驅動控制模型，對驅動控制輸出結果進行計算，完成旋轉機械的精準驅動控制。

1 旋轉機械運行狀態分析

1.1 并網光伏發電機組暫態響應計算

并網光伏發電機組是由若干個光伏組件、前級Boost 變換器和后級逆變器組成的大規模并網發電系統。與傳統靜止式發電機相比，在暫態電壓調度和一次能源的蓄電強度方面具有無法比擬的優勢。當發電機組中的旋轉機械開始運行時，需要對接入式電力系統低壓側和高壓側直流母線[3-4]的電容值同時測量，以保證能量轉化過程中的等效電壓和等效電流始終保持在額定電壓和額定電流以下。光伏組件的作用是對機組光伏滲透率進行疊加計算，以確保接入式電力系統直流母線電壓始終平穩，光伏滲透率[5]疊加計算公式為

式中：α 表示電力系統穩定運行狀態下的功角；q 表示并網變換器的勵磁電勢幅值；Δt 表示直流電壓的時間尺度；θi表示出口電壓基波分量。

設直流母線的電容值為ι，獲取并網光伏發電機組暫態響應計算公式為

式中：Δω 表示直流電容的參考電壓；pi表示并網變換器的電壓等級；pj表示電網電壓與輸出電壓之間的相位角。

1.2 旋轉機械動不平衡量計算

通過計算暫態響應，了解發電機組輸出電流和電壓發生的暫態波動情況，將其輸入至動不平衡量目標模型中，獲取準確的動態不平衡狀況與條件。為此，參考機械運動學理論，對旋轉機械的動平衡模型[6]進行建模，計算旋轉機械動不平衡量，以減小不平衡帶來的負面影響。建立的目標模型如式（3）所示：

基于建立的旋轉機械的動平衡模型，確定干擾力矩的分布情況，得到旋轉機械動不平衡量為

式中：δi，j表示第i 個旋轉軸中第j 個干擾力矩的位置信號表示旋轉軸轉角擾動系數表示旋轉軸的轉角。

1.3 獲取旋轉機械的運行狀態

旋轉機械由轉子、定子、轉軸以及永磁體組合而成，具有多變量、強耦合和非線性特征。通過計算并網光伏發電機組的暫態響應和旋轉機械動不平衡量，可以評估旋轉機械的運行質量。以此為基礎，對旋轉機械的內部結構建立一個數學模型，用來反映旋轉機械的運行狀態，并為驅動控制提供控制主體。

將并網光伏發電機組暫態響應及不平衡量輸入旋轉坐標系中，定義旋轉機械進行驅動控制的旋轉坐標系為H1，靜止的原始坐標系[8]為H2，自然坐標系為H3，與3 個坐標系對應的旋轉機械電機三相分別為a、b、c。對旋轉機械在自然坐標系H3下的電子電壓方程進行推理，得到：

式中：Ua、Ub、Uc分別表示電機三相的定子繞組電壓；R 表示電機三相定子繞組電阻[9]；Ia、Ib、Ic分別表示電機三相的定子繞組相電流；εa、εb、εc分別表示與電機定子繞組對應的磁鏈向量，表達公式為

式中：Ka、Kb、Kc分別表示電機三相繞組自感；φ 表示自然坐標系H3下的三相 角；Ja、Jb、Jc分別表示電機三相繞組互感；φ 表示旋轉機械轉子的永磁體磁鏈。

旋轉機械在自然坐標系H3下的轉矩方程表達式為

式中：ζ 表示旋轉機械擁有的轉子極對數。

在Clarke 變換算法的作用下，將自然坐標系下的旋轉機械變換到原始坐標系中，Clarke 變換方程如式（8）所示：

式中：η（q）表示經過Clarke 變換后與自然坐標系中三相電流矢量對應的原始坐標系中三相電流矢量；A 表示Clarke 變換矩陣；Iabc（q）表示自然坐標系中的旋轉機械三相電流矢量。

經過式（8）變換后，可得到靜止的原始坐標系下的旋轉機械數學模型，進而推理得到原始坐標系下的電壓方程為

式中：Ux、Uy、Uz分別表示旋轉機械在靜止時的三相等效電壓；Ix、Iy、Iz分別表示旋轉機械在靜止時的三相等效電流；εx、εy、εz分別表示旋轉機械在靜止時的三相等效磁鏈[10]。

經過Clarke 變換后，式（6）變換為

式中：Kx、Ky、Kz分別表示旋轉機械在靜止時的三相繞組自感；Jx、Jy、Jz分別表示旋轉機械在靜止時的三相繞組互感；ρ 表示旋轉機械的轉子角速度。

通過Clarke 變換將原始坐標系H2中的旋轉機械變換到旋轉坐標系H1中，使靜止的旋轉機械變換到運動狀態下，此時旋轉機械的運行狀態表達式為

式中：Gw表示旋轉坐標系H1下的旋轉機械磁鏈轉矩；U、I 分別表示旋轉機械的轉子電壓和電流。

通過建立旋轉機械驅動控制模型，可以監測旋轉機械的不同運動狀態，提高驅動控制的可靠性。

2 并網光伏發電機組旋轉機械驅動控制

VSG 中包含了直流電源、輸出LC 濾波器以及電力電子交換器等部件。在變換器中嵌入同步發生器的方程式，VSG 根據同步發生器的特性使直流電源和并網光伏發電機之間進行功率交換，以此實現對旋轉機械的驅動控制。VSG 拓撲結構如圖1 所示。

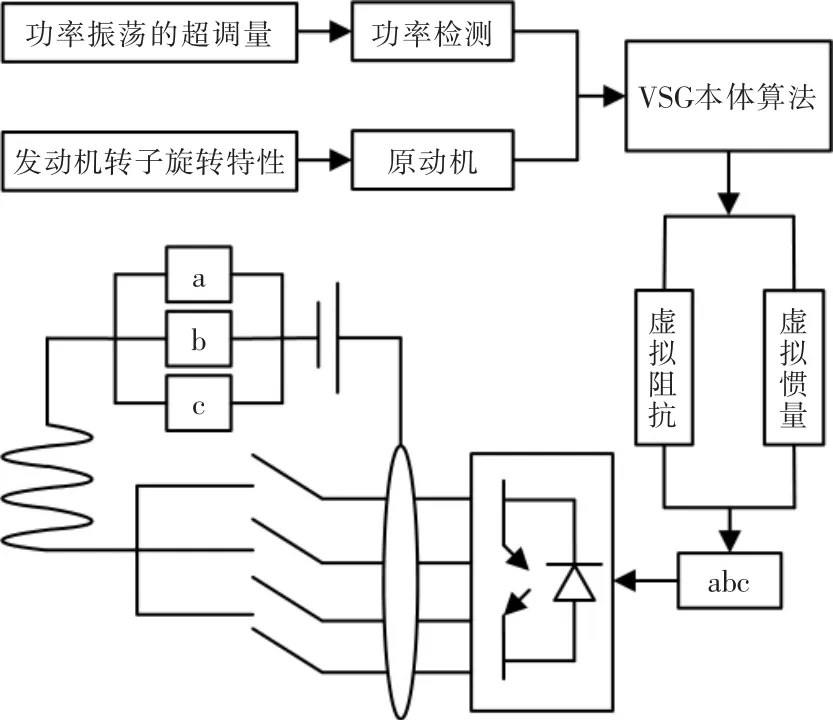
圖1 VSG 拓撲結構圖Fig.1 VSG topological structure diagram

二階W、三階S、五階P 模型表達式分別為

式中：gi表示旋轉機械中轉子的轉速；ν 表示衰減因子；Δb 表示期望阻尼；λa表示阻尼偏差；o′表示模型的權重值；u 表示慣性響應的時間間隔；Yn表示旋轉機械轉子角頻率基準值；s1、s2分別表示有功負荷擾動閾值和聯絡線功率振蕩幅值。

通過上述技術，建立基于VSG 的旋轉機械驅動控制模型，將VSG 本體算法作為驅動控制的核心算法，同時結合VSG 控制策略，得到基于VSG 的旋轉機械驅動控制模型。

VSG 本體算法表達式如式（13）所示：

式中：μn、μm分別表示旋轉機械轉子角速度和線速度；R′表示加入負荷擾動后旋轉機械轉子的暫態持續時間。由此，獲取旋轉機械驅動控制的輸出結果為

式中：κ0表示擾動周期的抑制頻率；χ 表示功率譜初始變化率；yˉ表示旋轉機械轉子的初始存儲動能。

根據式（14）的計算結果，實現對并網光伏發電機組旋轉機械的驅動控制。

3 實驗測試

為了驗證所提方法是否可以實現理想的驅動控制，展開實驗測試分析。并網光伏發電機組中應用的為IHFA-AF47 型號旋轉機械，電壓330 V，功率7.56 kW，氣流方向為軸流式，旋轉直徑為756.45 mm，共有7 片葉片。利用Simulink 仿真軟件包對并網光伏發電機組電路進行模擬，拓撲結構圖及實驗各項參數設置如圖2、表1 所示。

表1 實驗參數設置Tab.1 Experimental parameter settings

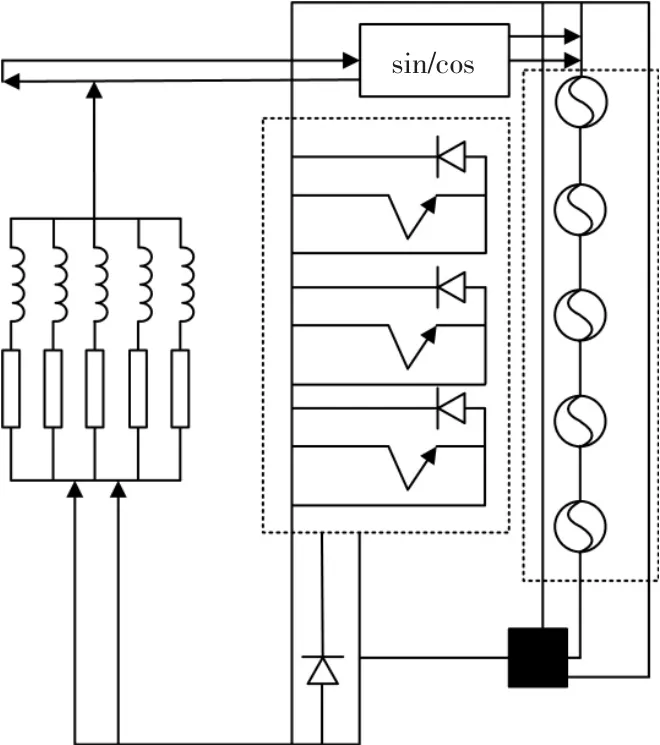
圖2 并網光伏發電機組模擬電路拓撲結構圖Fig.2 Topological structure diagram of the analog circuit of grid connected photovoltaic generating units

3.1 機械振幅測試

控制算法的電壓值決定了機械振幅的表現形式，振幅越大，說明控制算法的可靠性越差；反之，則說明控制算法的可靠性越高。所提方法的機械振幅如圖3 所示。

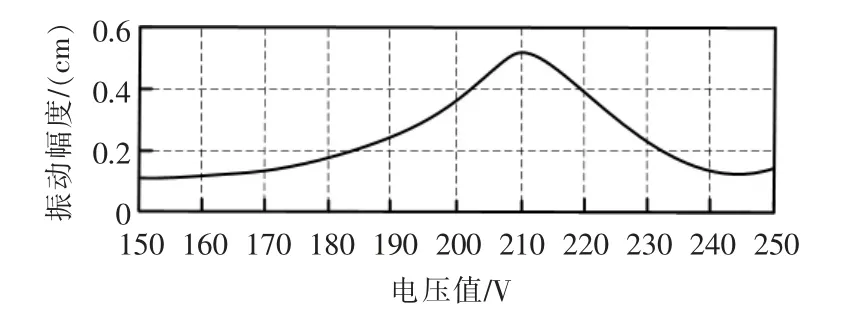
圖3 機械振幅測試Fig.3 Mechanical amplitude test

通過圖3 可知，隨著電壓值的不斷升高，機械振幅也隨之增加，直至電壓值達到210 V 時為振幅峰值，之后隨著電壓值的增加振幅出現下降趨勢，振動幅度始終未超過0.6 cm，說明了該方法的可靠性。

3.2 控制響應時間測試

在控制請求數量不斷變化的前提下，測試所提方法的控制響應時間。在發送控制請求的那一刻為起始時間，旋轉機械驅動運行為終止時間，響應時間如圖4 所示。

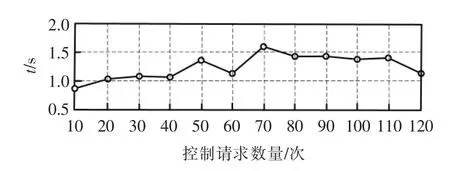
圖4 控制響應時間測試Fig.4 Control response time test

從圖4 中可以看出，控制響應時間較短，平均為1.28 s，數值較小，說明可以針對旋轉機械實現實時控制。

3.3 控制精度測試

失控率可以在一定程度上反映出算法的控制精度，計算公式為

式中：w 表示旋轉機械驅動控制失敗次數；r 表示旋轉機械驅動控制成功次數。利用式（15）計算所提方法的失控率，結果如圖5 所示。

圖5 失控率測試Fig.5 Loss of control rate test

從圖5 中可以看出，隨著控制次數的不斷增加，所提方法的失控率雖然呈上升趨勢，但未超過7.5%，說明該方法的控制精度較高，滿足設計要求。

4 結語

針對并網光伏發電機組中存在的問題，提出一種旋轉機械驅動控制方法。通過分析并網光伏發電機組暫態響應和計算旋轉機械動不平衡量，建立旋轉機械驅動控制數學模型，獲取旋轉機械的運行狀態。建立基于VSG 的旋轉機械驅動控制模型，將VSG 控制策略作為模型的外骨架、VSG 本體算法作為核心算法，實現對旋轉機械的驅動控制。實驗結果表明，所提方法具有較高的控制可靠性和控制效率，同時可以有效提高驅動控制精度。