不同結構參數對高速開關閥液壓力的影響研究*

趙才虎,陳 譽,,3*,朱天龍,孫寶林,張 晉

(1.南京工程學院 機械工程學院,江蘇 南京 211167;2.燕山大學 機械工程學院,河北 秦皇島 066004;3.海天塑機集團有限公司,浙江 寧波 315823)

0 引 言

高速開關閥具有低廉的價格和卓越的抗污染性能,同時具有快速響應和高頻率開關能力,使其在工業(yè)自動化、能源、航空航天等領域得到了廣泛應用。隨著科技的不斷發(fā)展,高速開關閥有望在更多領域得到應用。

目前,大部分高速開關電磁閥采用的是開關控制方式。將其應用于車輛制動領域時,這種控制方式容易產生較大的壓力沖擊,加劇制動系統(tǒng)噪聲,使踏板舒適性變差[1]。隨著對其性能要求的不斷提高,通過對高速開關閥液壓力進行數值特性研究與優(yōu)化,分析閥芯受力的影響因素,可以提高閥控制的穩(wěn)定性,為高速開關電磁閥的線性控制設計提供理論基礎[2-4]。

液壓油流過閥口時,閥芯對液壓油的阻礙會導致液壓油流動的方向和速度大小發(fā)生改變。依據牛頓第三定律,液壓油同樣對閥芯產生一個相應的反作用力,稱之為液壓力。目前,國內外學者對高速開關閥液壓力展開了大量研究并取得了一些成果。

DAI J等人[5]采用實驗和數值模擬方式,研究了液壓力對高速電磁閥動態(tài)特性的影響。ZHANG Y等人[6]研究了伺服閥中液壓力對動態(tài)特性的影響,采用實驗和數值模擬的方式,探討了液壓力對伺服閥的頻率響應、響應時間和線性度等性能的影響。萬理平[7]利用CFD軟件中的多孔介質,模擬了實際濾網對高速開關閥流場的影響,結果表明,濾網目數越大對閥的節(jié)流作用越大,流體對閥芯的作用力越小。ZHU X等人[8]研究了比例控制閥中液壓力對流量特性的影響,采用實驗和數值模擬方式,研究了液壓力對比例控制閥的流量響應、線性度和能耗等性能的影響。LI Y等人[9]基于計算流體力學和侵蝕理論,建立了閥口侵蝕的三維預測模型,分析了不同因素下閥口侵蝕的變化規(guī)律。LI M等人[10]強調了在實現(xiàn)精確可靠的液壓力控制方面所面臨的挑戰(zhàn),包括非線性、滯后效應和外部干擾等;還介紹了改進液壓力控制的各種解決方案和策略,包括先進的控制算法、傳感器技術和系統(tǒng)設計考慮。

現(xiàn)有的研究主要集中在液壓力對電磁閥的性能影響方面,缺乏流體介質等因素對液壓力影響的研究。

筆者基于制動系統(tǒng)中高速開關閥的物理模型,利用流體仿真技術對閥芯液壓力進行數值特性研究,分析作用在閥芯上的液壓力影響因素,為精確研究高速開關閥的動態(tài)特性提供理論依據。

1 高速開關閥流場仿真模型

高速開關閥通常是二通二位的電磁閥[11],主要由隔磁管、動鐵、推桿、閥鐵、閥座、彈簧等組成。

其結構簡圖如圖1所示。

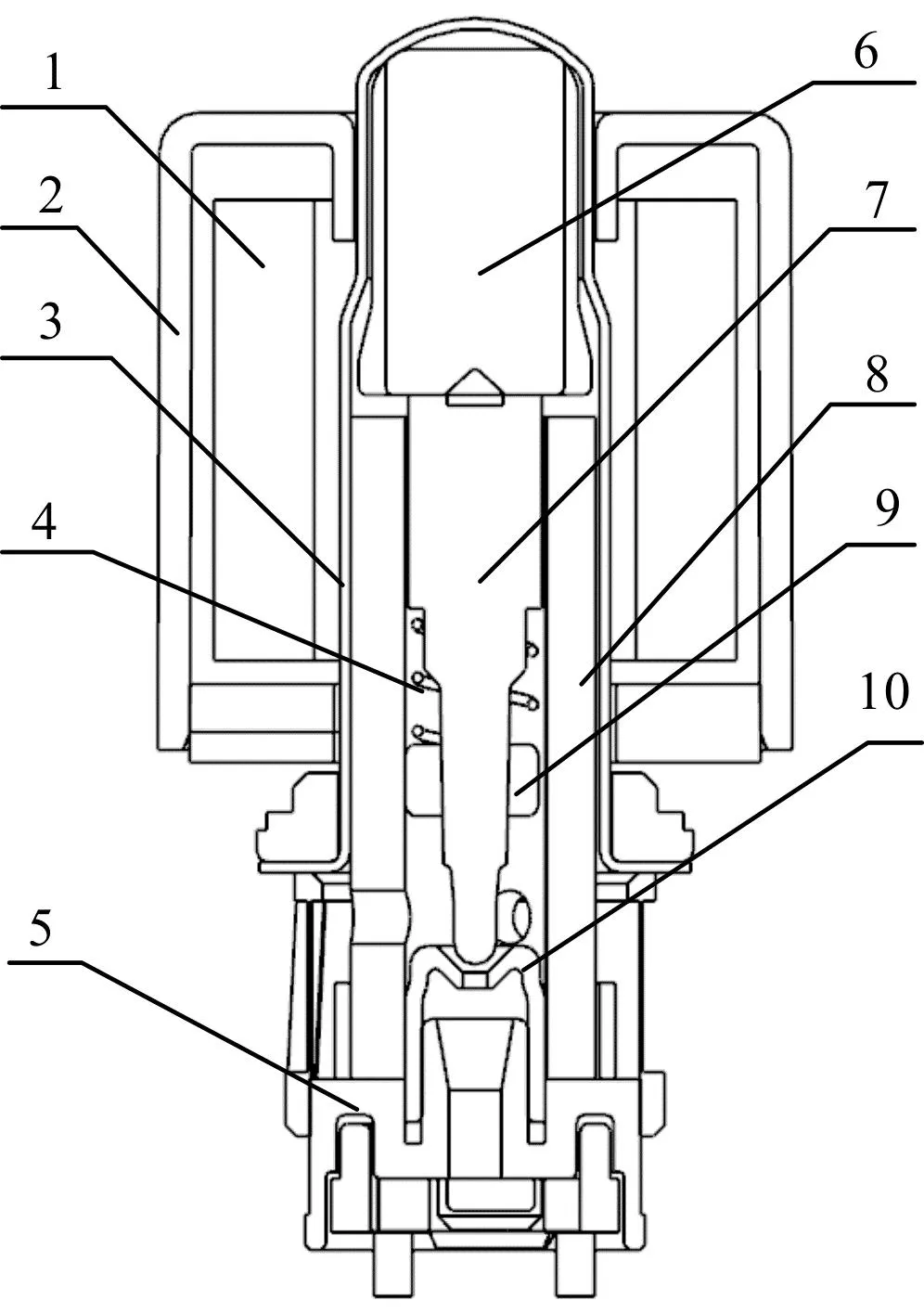
圖1 高速開關閥結構簡圖Fig.1 Schematic diagram of a high-speed switch valve1為線圈;2為軛鐵;3為隔磁管;4為彈簧;5為濾網座;6為動鐵;7為閥芯;8為閥體;9為擋圈;10為閥座。

圖1中,動鐵在磁場中受電磁力驅動,沿著軸向進行運動,從而控制閥芯進行往復運動。

高速開關閥在工作時,其閥芯受到電磁力、彈簧力、液壓力等力的耦合作用,液壓力是影響閥控制穩(wěn)定性的關鍵因素。

閥芯受力示意圖如圖2所示。

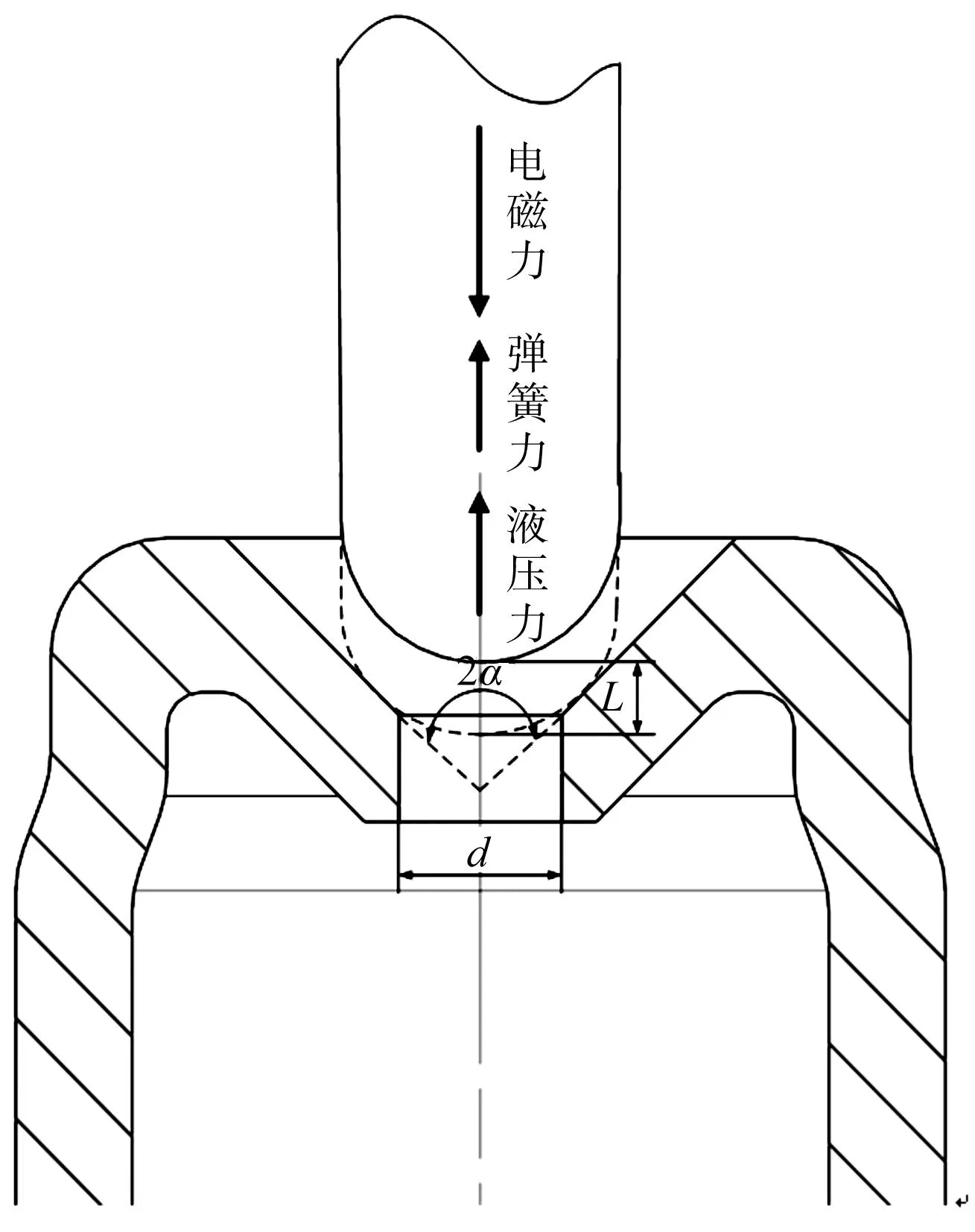
圖2 閥芯受力示意圖Fig.2 Schematic diagram of the forces acting on the valve spool

筆者定義開度L為閥芯從閉合狀態(tài)向上移動的距離,液壓力向上為正方向,閥座節(jié)流孔直徑為d,閥座錐角為2α。通常高速開關閥的行程是毫米級,其響應時間是毫秒級。

1.1 物理模型與網格劃分

基于三種不同方案,筆者建立電磁閥流體域三維模型。

開度為0.01 mm、閥座錐角為90°時,高速開關閥的流體域三維模型如圖3所示。

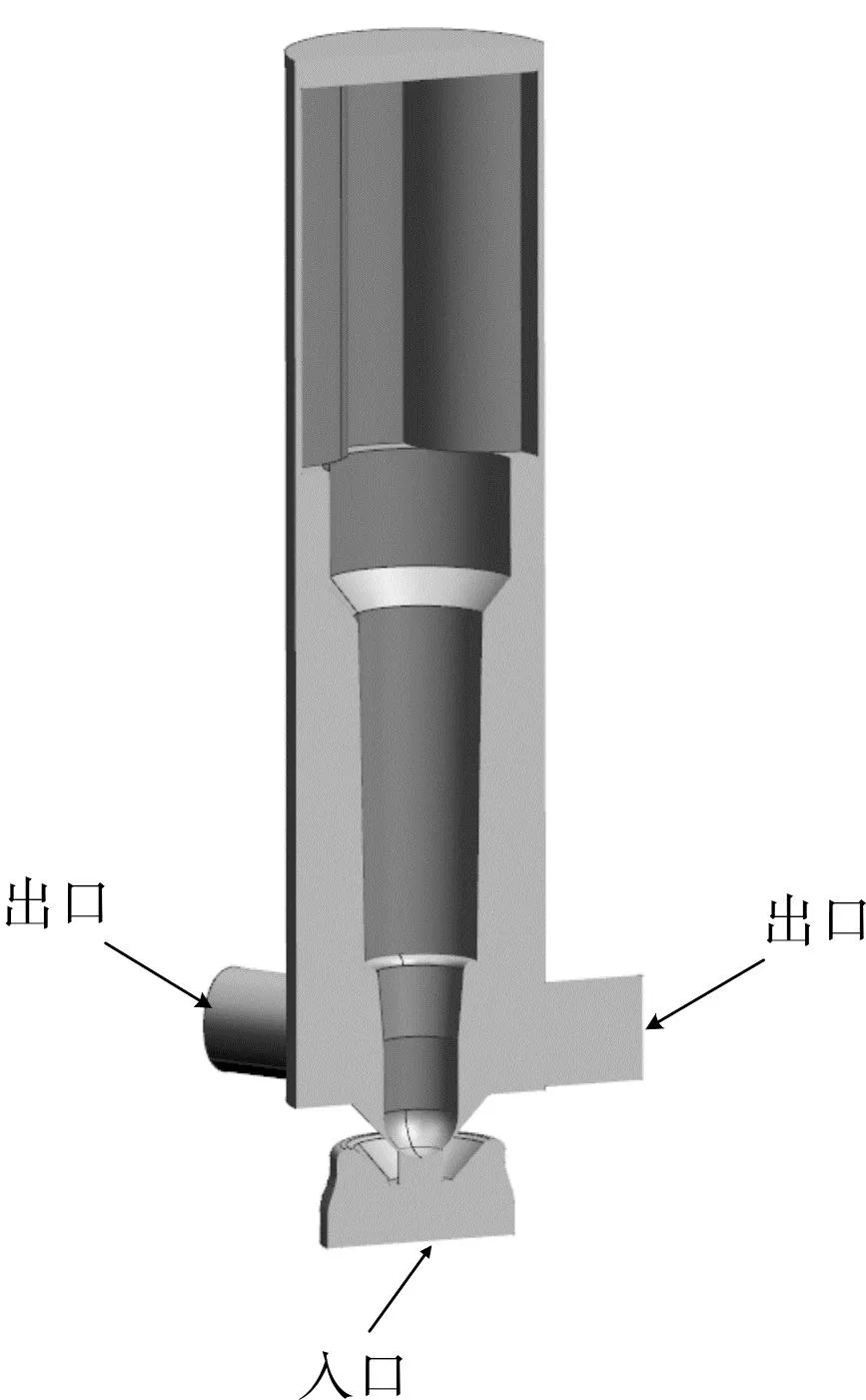
圖3 流體域三維模型剖視圖 Fig.3 Three-dimensional sectional view of the fluid domain model

方案一。節(jié)流孔直徑為0.7 mm,閥座錐角為90°,開度范圍為0.01 mm～0.04 mm,以0.01 mm為間隔;開度范圍為0.04 mm～0.22 mm,以0.02 mm為間隔,建立各開度的仿真模型;

方案二。開度為0.01 mm、0.04 mm、0.10 mm,閥座錐角為90°,節(jié)流孔直徑為0.6 mm、0.7 mm、0.8 mm、0.9 mm,建立不同孔徑的仿真模型;

方案三。開度為0.01 mm、0.04 mm、0.10 mm,節(jié)流孔直徑為0.7 mm,閥座錐角為60°、70°、80°、90°、120°,建立不同閥座角度的仿真模型。開度為0.01 mm、節(jié)流孔直徑為0.7 mm、閥座錐角為90°。

閥口網格劃分如圖4所示。

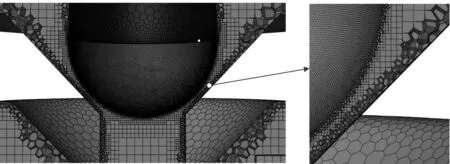
圖4 閥口網格劃分模型Fig.4 Mesh distributions near the valve orifice

筆者采用“Poly-Hexcore”網格對仿真模型進行網格劃分,使六面體網格與多面體網格實現(xiàn)共節(jié)點連接,從而提升網格中六面體的數量,以達到提升求解效率與精度的目的。

由于閥口開度很小,閥口處壓力與流速變化梯度很大,所以需要對閥口進行網格細化。

1.2 仿真介質與邊界條件

筆者選用DOT4液壓油作為流體介質進行仿真計算。

其動力黏度隨溫度的變化情況如表1所示。

表1 不同溫度下DOT4液壓油的動力黏度Table 1 Dynamic viscosity of DOT4 hydraulic oil at different temperatures

進出口邊界條件分別設為壓力進口和壓力出口。具體壓力值及對應的壓差如表2所示。

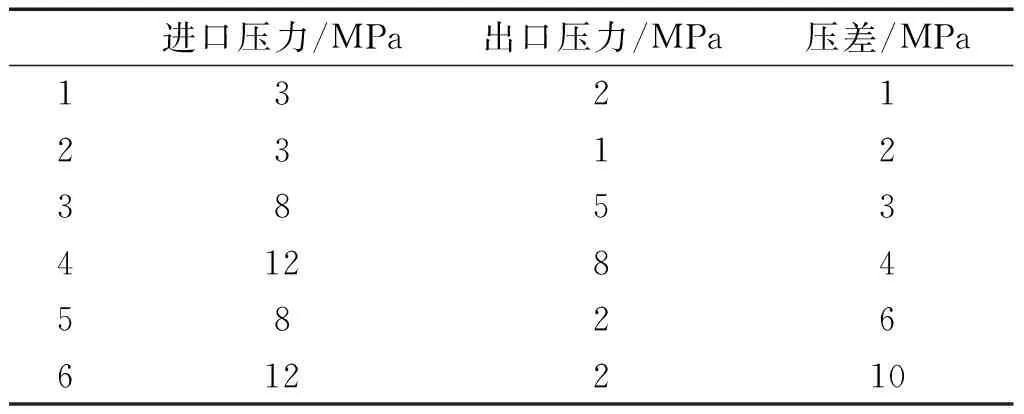
表2 進出口壓力設置Table 2 Inlet and outlet pressure settings

1.3 仿真模型選擇

筆者研究的開關閥響應速度快、頻率高。在進出口壓差較小的情況下,不考慮空化現(xiàn)象,宜選取標準k-ε湍流模型。該模型適合完全湍流的流動過程模擬,近壁處理采用標準的壁面函數,它能夠為大多數高雷諾數的邊界限制流動提供合理、精確的預測[12]。

k-ε湍流方程如下所示:

(1)

(2)

式中:Gk為平均速度梯度引起的湍流動能;Gb為浮力引起的湍流動能;YM為可壓縮湍流脈動膨脹對總耗散率的影響。

各個常數保持默認值,湍動能與耗散率的湍流普朗特數分別為σk=1.0,σε=1.3。

2 仿真結果與分析

2.1 網格無關性驗證

筆者進行網格獨立性驗證,以排除網格數量對于仿真結果的影響。筆者共劃分了四套網格,分別包括6.7×105、9.0×105、1.32×106和1.86×106個網格。

筆者對比不同網格數量的速度分布和流線分布云圖發(fā)現(xiàn),當網格數目大于1.32×106個后,流體速度和流線分布趨勢基本相同。

不同網格速度分布云圖如圖5所示。

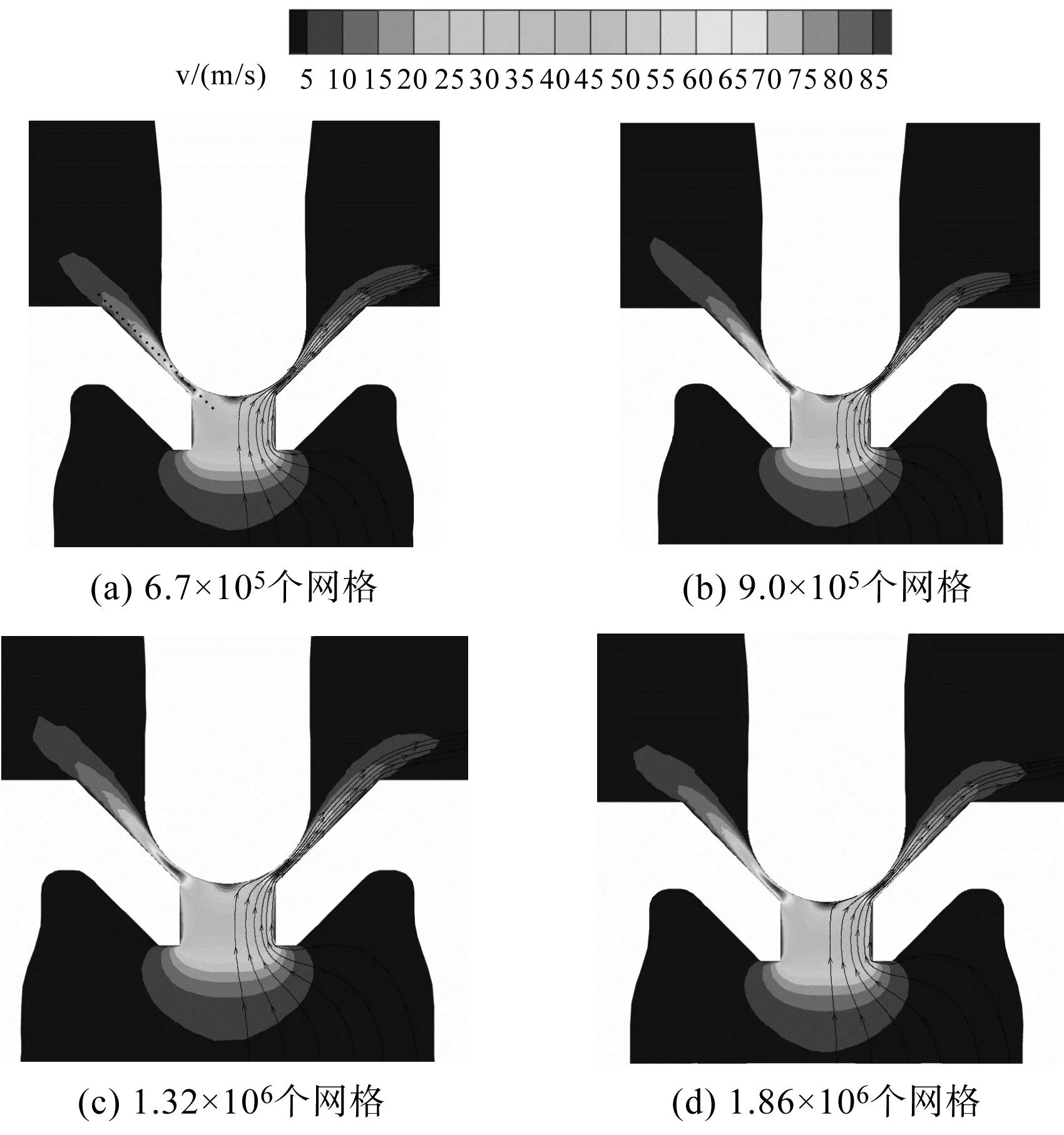
圖5 不同網格速度分布云圖Fig.5 Velocity distribution contours for different grid sizes

圖5(a)中,筆者對比不同網格數量閥口處沿錐面的流速與壓強變化,取20個點,讀取各個點的流速與壓力數值。

不同網格下錐面流速和壓力變化如圖6所示。

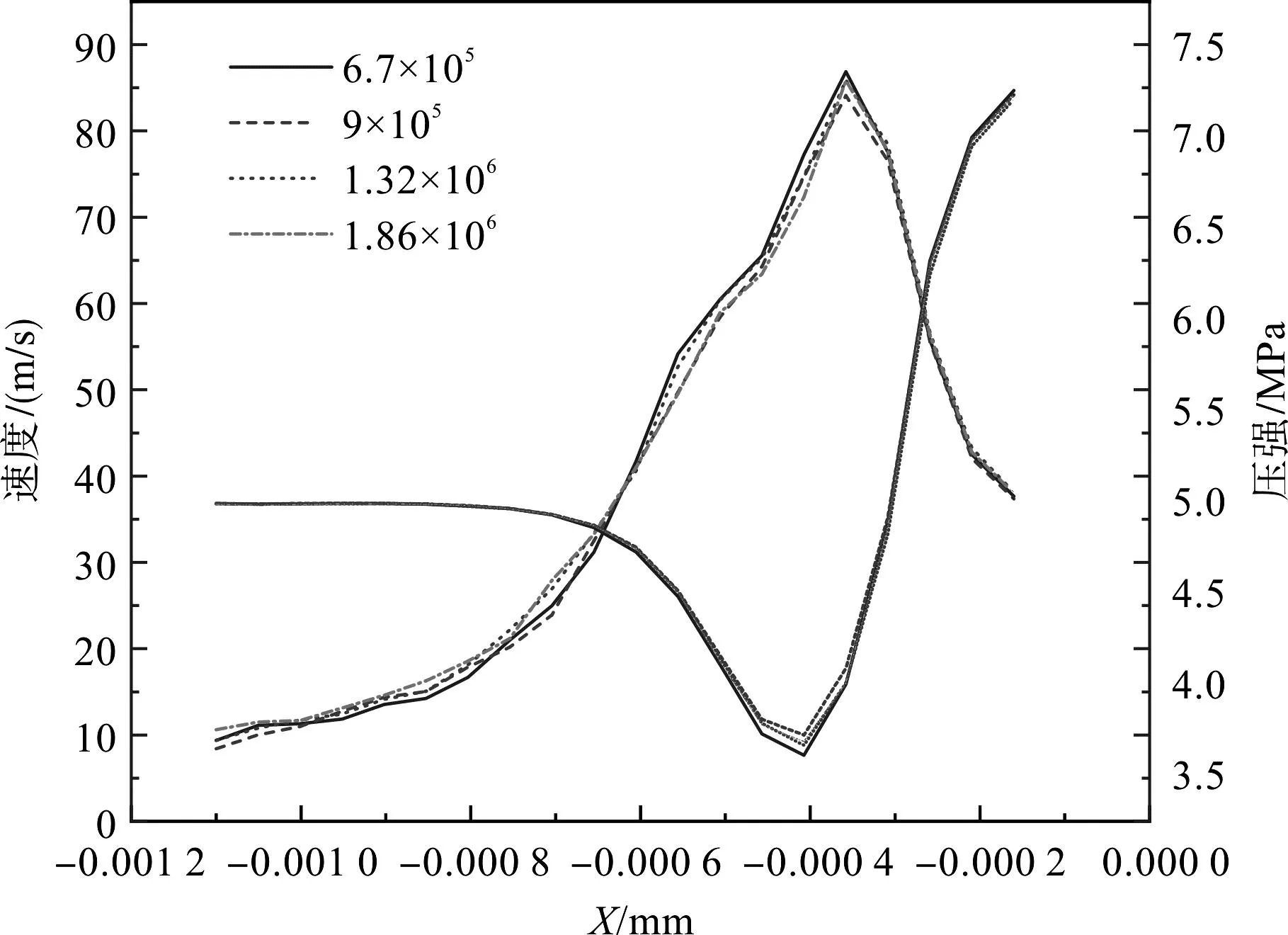
圖6 不同網格下錐面流速和壓力變化圖Fig.6 Velocity and pressure near the cone surface for different grid sizes

從圖6中可以看出:網格數目大于1.32×106個后,流速與壓力分布基本相同,網格數目對于流場分布的影響可以忽略。

因此,筆者最終確定1.32×106個網格為仿真研究中精度和效率之間的最佳選擇。

2.2 閥口開度對液壓力的影響

筆者選定流體介質溫度為20 ℃、進出口壓差為3 MPa,對方案一模型的所有工況進行流場仿真。

液壓力與開度的關系如圖7所示。

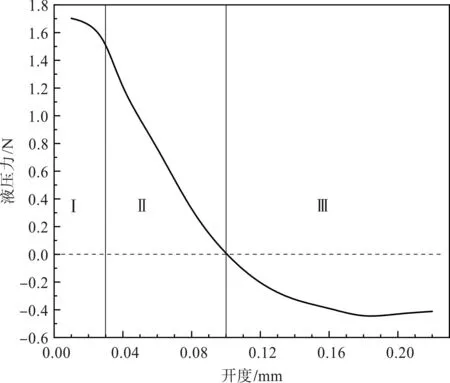
圖7 液壓力與開度的關系曲線圖 Fig.7 Relationship between hydraulic pressure and valve opening

區(qū)域Ⅰ。曲線開口向下,在開度0.03 mm左右出現(xiàn)拐點。在這個區(qū)域內,隨著閥門開度的增加,液壓力下降,這表明閥口節(jié)流在這個區(qū)域內占主導節(jié)流;隨著閥門開度增加,閥口的壓降增加,導致液壓力下降。

區(qū)域Ⅱ。隨著閥門開度進一步增加,液壓力急劇下降,在開度為0.08 mm左右降為零。曲線在這個區(qū)域呈現(xiàn)良好的線性關系,表明液壓力與閥門開度之間存在強烈的線性相關性;這表明仍由閥口主導節(jié)流作用,隨著閥門開度的增加,閥口的壓降呈線性增加,導致液壓力下降。

區(qū)域Ⅲ。液壓力變?yōu)樨撝?曲線近似為開口向上的拋物線。在這個區(qū)域內,隨著開度的增加,液壓力的絕對值逐漸增加,約在開度為0.18 mm左右達到最大值;然后,隨著開度的進一步增加而稍有下降。這表明主導節(jié)流作用的區(qū)域從閥口轉移到了閥座節(jié)流孔,閥座節(jié)流孔的壓降是導致液壓力下降的主要原因。

流體介質溫度為20 ℃、進出口壓差為3 MPa時,不同閥門開度的壓強分布如圖8所示。

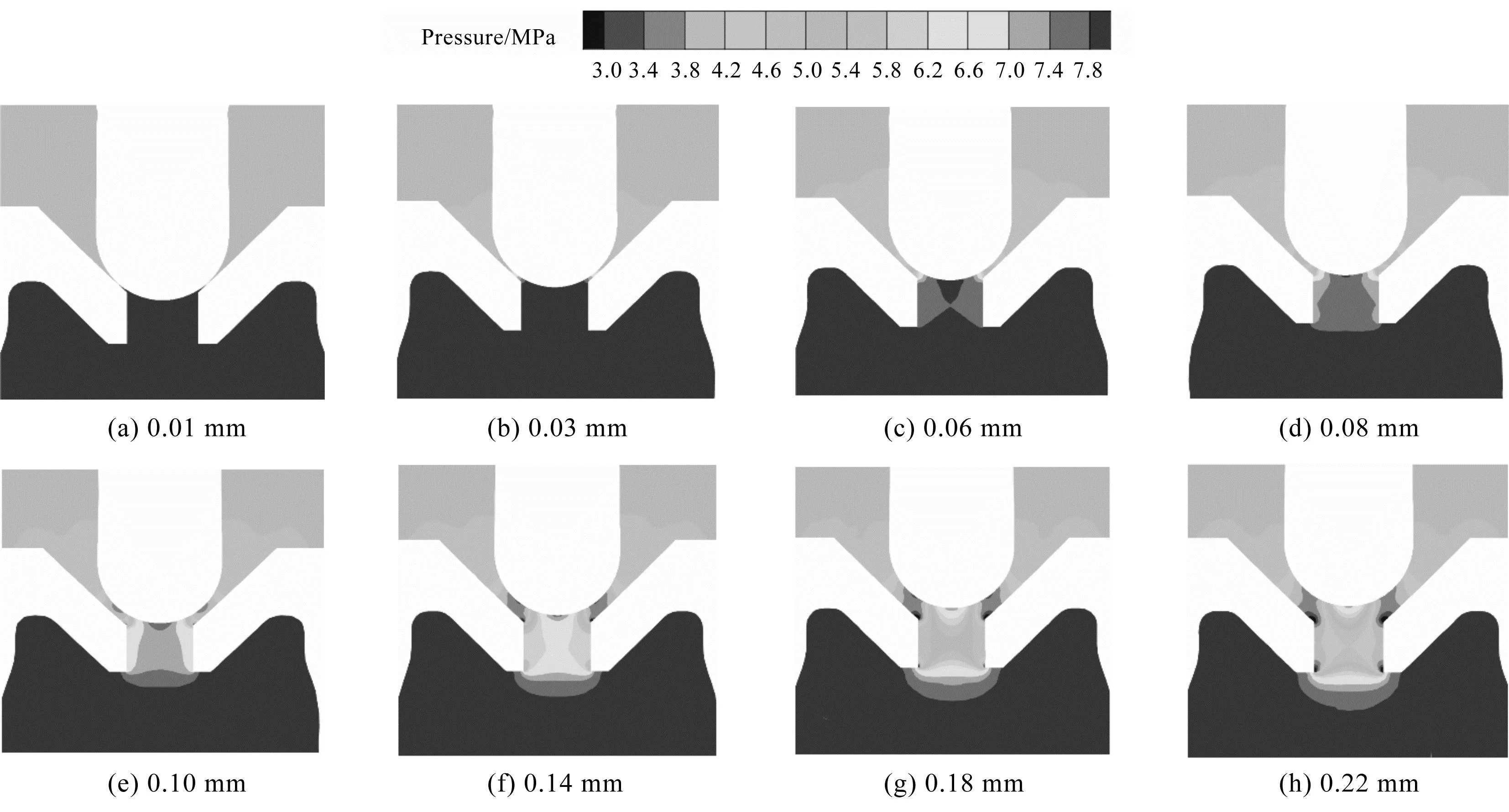
圖8 不同開度的壓強分布云圖Fig.8 Pressure distributions for different openings

從圖8中可以看出:流體通過閥口狹窄處,壓力梯度迅速下降;隨著開度逐漸增加,閥座節(jié)流孔壓強逐漸下降;

圖8(g)中的節(jié)流孔處壓強(5 MPa)明顯小于圖8(d)處的壓強值(8 MPa)。

筆者沿著閥座壁面,取不同高度的點,讀取各個點的壓強值,探究不同開度閥口的壓強變化情況。

開度為0.18 mm時,閥口速度分布及所取壓強點位置如圖9所示。

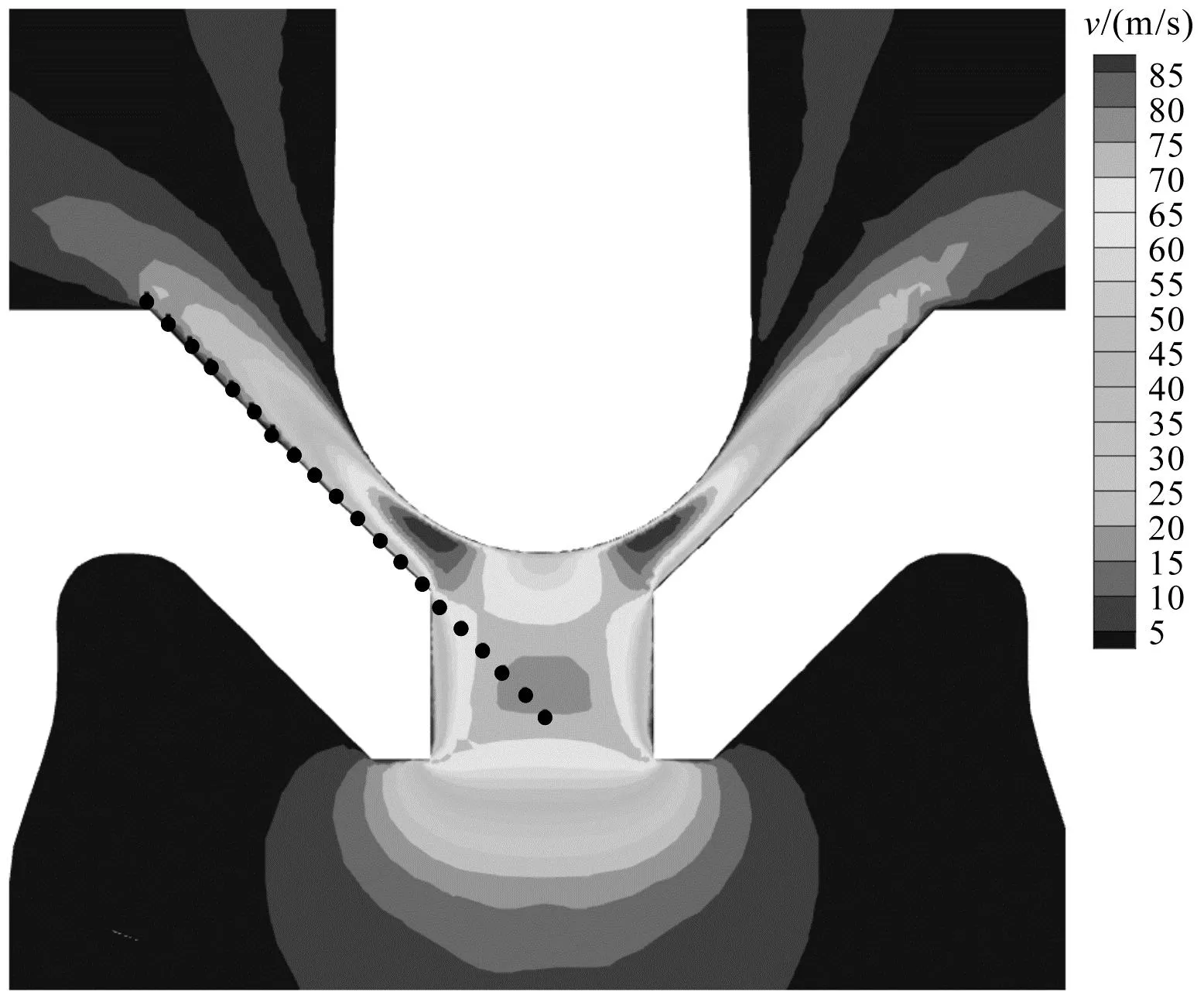
圖9 0.18 mm開度閥口速度云圖Fig.9 Velocity contours at 0.18 mm opening

不同開度錐面壓力變化如圖10所示。

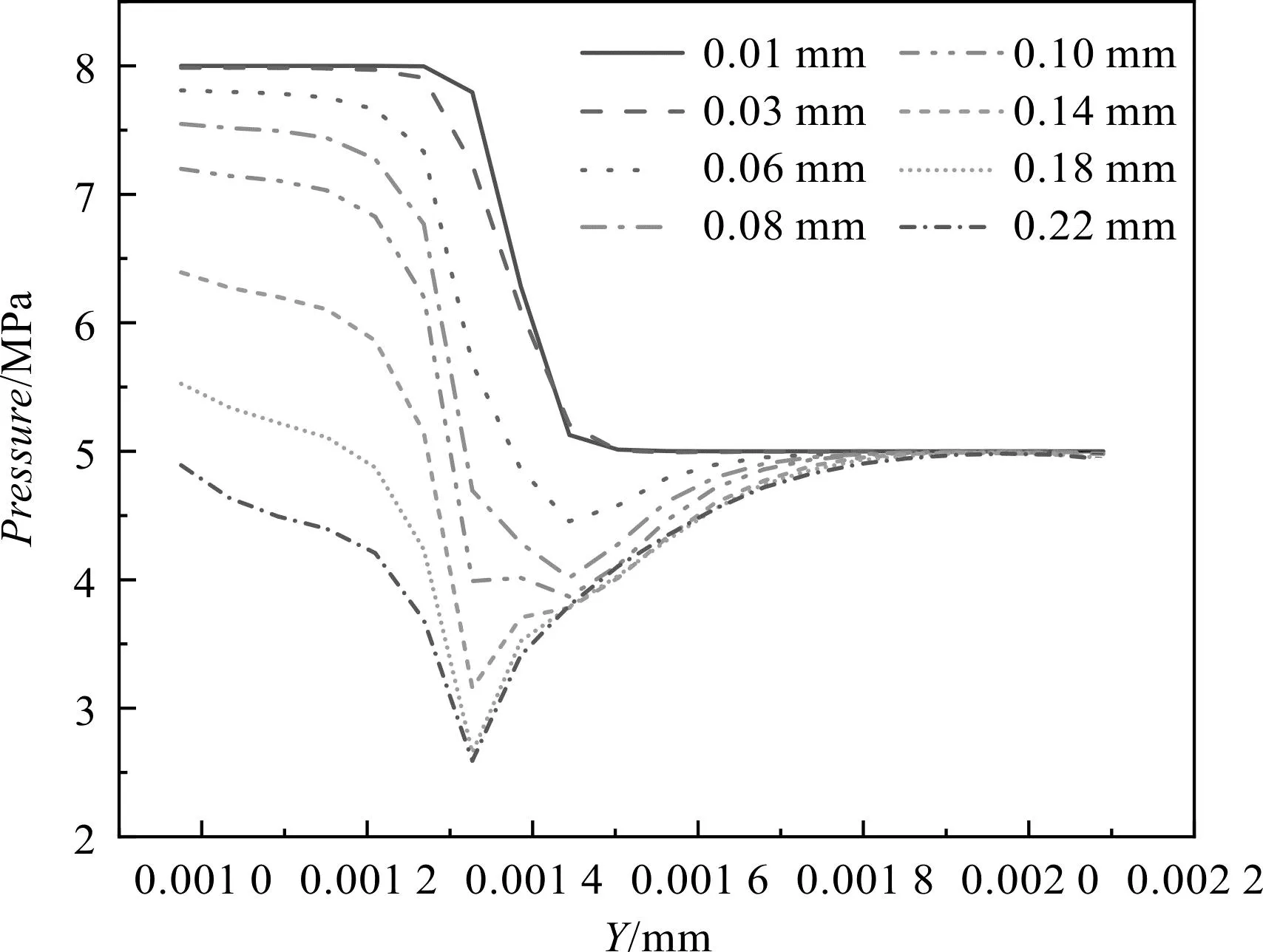
圖10 不同開度錐面壓力變化Fig.10 Pressure variation on the conical surface for different openings

圖10中,對于較小的開度(0.01 mm～0.10 mm),在節(jié)流孔處(即橫坐標Y值較小)壓強很大,未發(fā)生明顯壓降,在閥口產生明顯壓降,最后回歸到出口壓強5 MPa。對于較大的閥口開度(0.14 mm～0.22 mm),在節(jié)流孔處有著明顯的壓降,雖然閥口也有壓降,但壓降的梯度明顯沒有(0.01 mm～0.10 mm)開度大,最后回歸至出口壓強5 MPa。

在開度逐漸增大的過程中,初始階段節(jié)流效應主要由閥口決定,流體在閥口處發(fā)生了顯著的壓降。然而,隨著開度進一步增大,節(jié)流區(qū)域從閥口轉向閥座節(jié)流孔;當開度為0.18 mm時,節(jié)流效應主要由閥座節(jié)流孔決定,進一步增大開度并不會增加液壓力。閥座節(jié)流孔處壓強低,表明流經此處的油液流速很高。

正如圖9中所示:在閥座節(jié)流孔處存在高速流體流動,說明閥座孔口處存在節(jié)流效應。

2.3 壓差對液壓力的影響

針對方案一,筆者選取流體介質溫度為20 ℃,進出口壓差分別為1 MPa、2 MPa、3 MPa、4 MPa、6 MPa、10 MPa,探究壓差變化對液壓力的影響。

在0.02 mm開度,不同壓差速度分布如圖11所示。

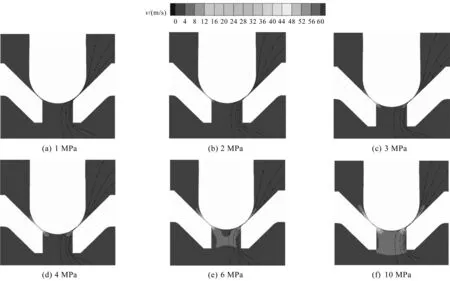
圖11 不同壓差的速度云圖Fig.11 Velocity contours for various pressure differences

從圖11中可以看出:壓差越大,閥口的流速越快,流速的增速也越快。

不同壓差下,液壓力與開度的關系如圖12所示。

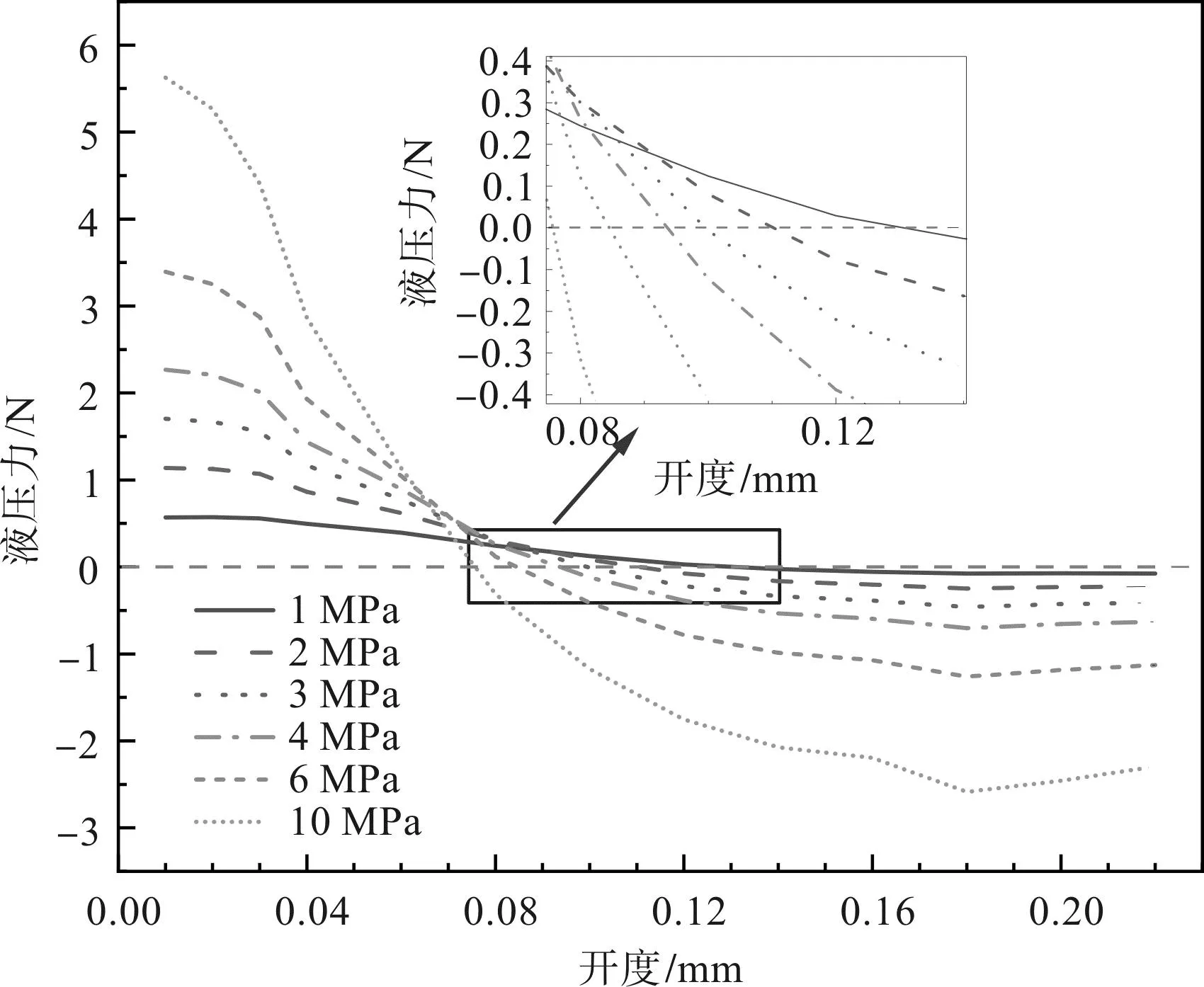
圖12 不同壓差下液壓力與開度關系曲線Fig.12 Hydraulic pressure against valve opening for various pressure differences

圖12中,在相同溫度條件下,壓差越大、液壓力變化幅度越大。

從局部放大圖可以看出:壓差越大,曲線與液壓力為0(虛線所示)的交點橫坐標越小,即壓差越大,正向液壓力所處開度范圍越小,閥芯可控開度范圍越小。這是因為壓差越大,小開度狀態(tài)下流速的增速越快,閥口處的低壓和負壓所占面積越大,因此壓差越大,則液壓力變化范圍越大。

此外,在同一開度下,液壓力增幅與壓差的增幅近似成正比,表明液壓力與壓差之間存在線性關系。

不同閥口開度下,壓差與液壓力之間的關系如圖13所示。

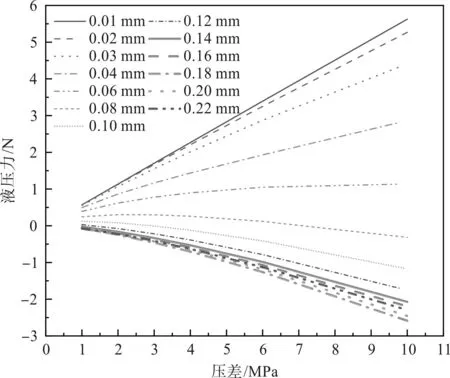
圖13 不同開度下液壓力與壓差關系曲線 Fig.13 Hydraulic pressure against pressure difference for various valve openings

圖13表明:在小開度范圍(0.01 mm～0.06 mm),液壓力與壓差近似成正比;而在較大的開度范圍(0.08 mm～0.22 mm),液壓力與壓差近似成反比,且隨著開度增加,曲線的斜率在不斷減小。

研究結果表明:在高速開關閥中,閥進出口的壓差對液壓力有顯著影響,較大的壓差導致液壓力的變化更大,同時使得閥芯開度的可控范圍變小。液壓力和壓差之間的關系復雜,并且取決于開度,小的開度下呈線性關系,而較大的開度下呈反比關系。

這些研究結果對于優(yōu)化高速開關閥的設計有較大價值。

2.4 溫度對液壓力影響

筆者在1.1節(jié)的方案一中選定工作壓差為3 MPa,溫度分別為-40 ℃、-20 ℃、0 ℃、20 ℃、40 ℃、60 ℃、80 ℃,探究流體介質溫度變化對閥芯液壓力的影響。

不同溫度下,液壓力與開度關系的曲線圖如圖14所示。

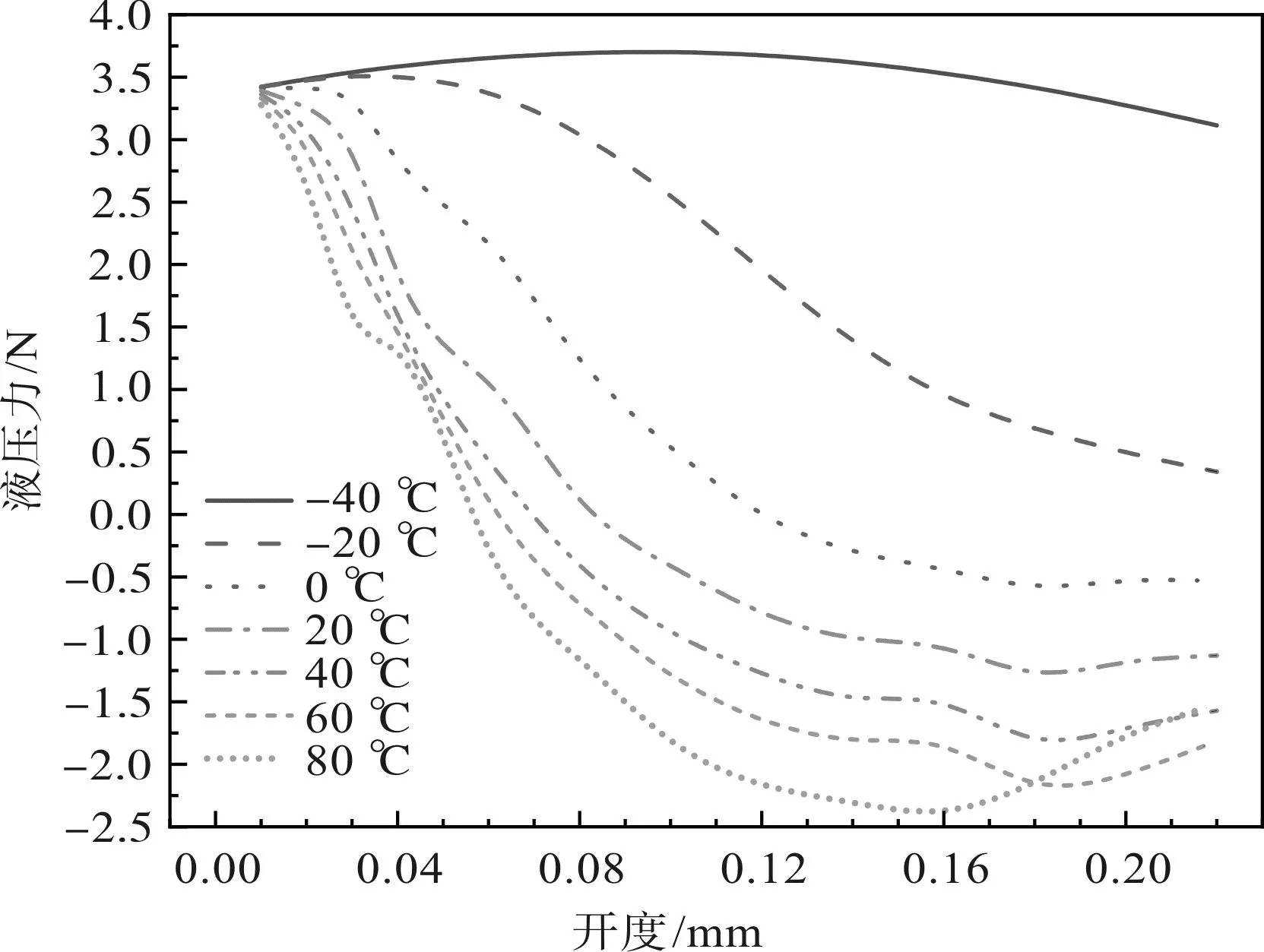
圖14 不同溫度下液壓力與開度關系曲線圖Fig.14 Hydraulic pressure against valve opening for different temperatures

從圖14中可以看出:低溫對液壓力有很大影響,高溫對液壓力影響較小。隨著溫度降低,曲線開口在不斷變小,到-40 ℃時開口已變成負值。

溫度相關系數矩陣如圖15所示。

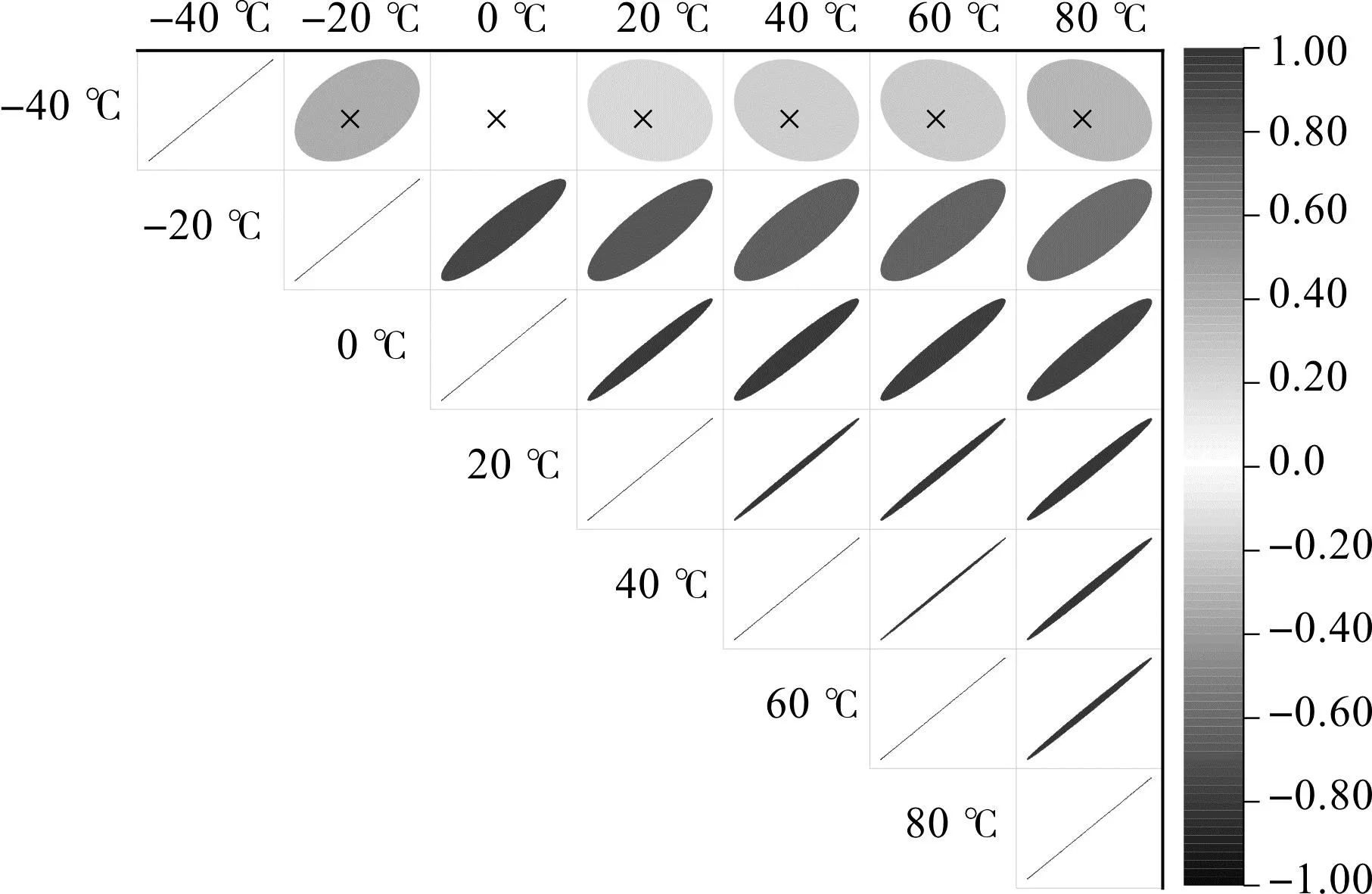
圖15 各溫度相關系數矩陣圖Fig.15 Correlation coefficient matrix for different temperatures

圖15中,相關系數值越大,橢圓越扁平,打“×”表示兩者之間相關性不顯著。

圖15進一步支持了圖14的研究結果,其顯示-40 ℃與其他溫度沒有顯著相關性,并且具有負相關系數。另一方面,高溫之間呈現(xiàn)強烈的相關性,說明在較高溫度下,溫度對液壓力的影響較小。

流體的動力黏度隨溫度的變化如圖16所示。

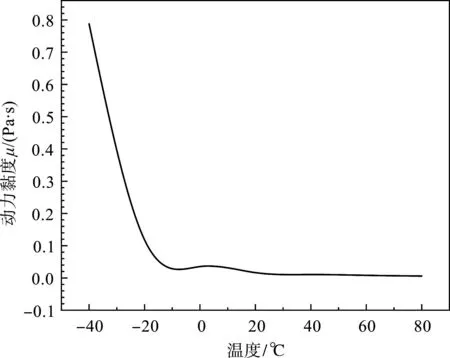
圖16 不同溫度液壓油動力黏度 Fig.16 Dynamic viscosity of hydraulic oil at different temperatures

在-40 ℃和-20 ℃之間,動力黏度變化為0.67 Pa·s,變化幅度最大。這表明在低溫條件下,溫度的變化可以導致動力黏度的顯著變化,從而引起液壓力的大幅變化。然而,在高溫條件下,溫度對動力黏度的影響較小,液壓力的變化也較小。同時,因為動力黏度的變化會影響閥內部流場分布特性,導致出口流量變化。

不同溫度下,各開度的流量及部分速度變化如圖17所示。

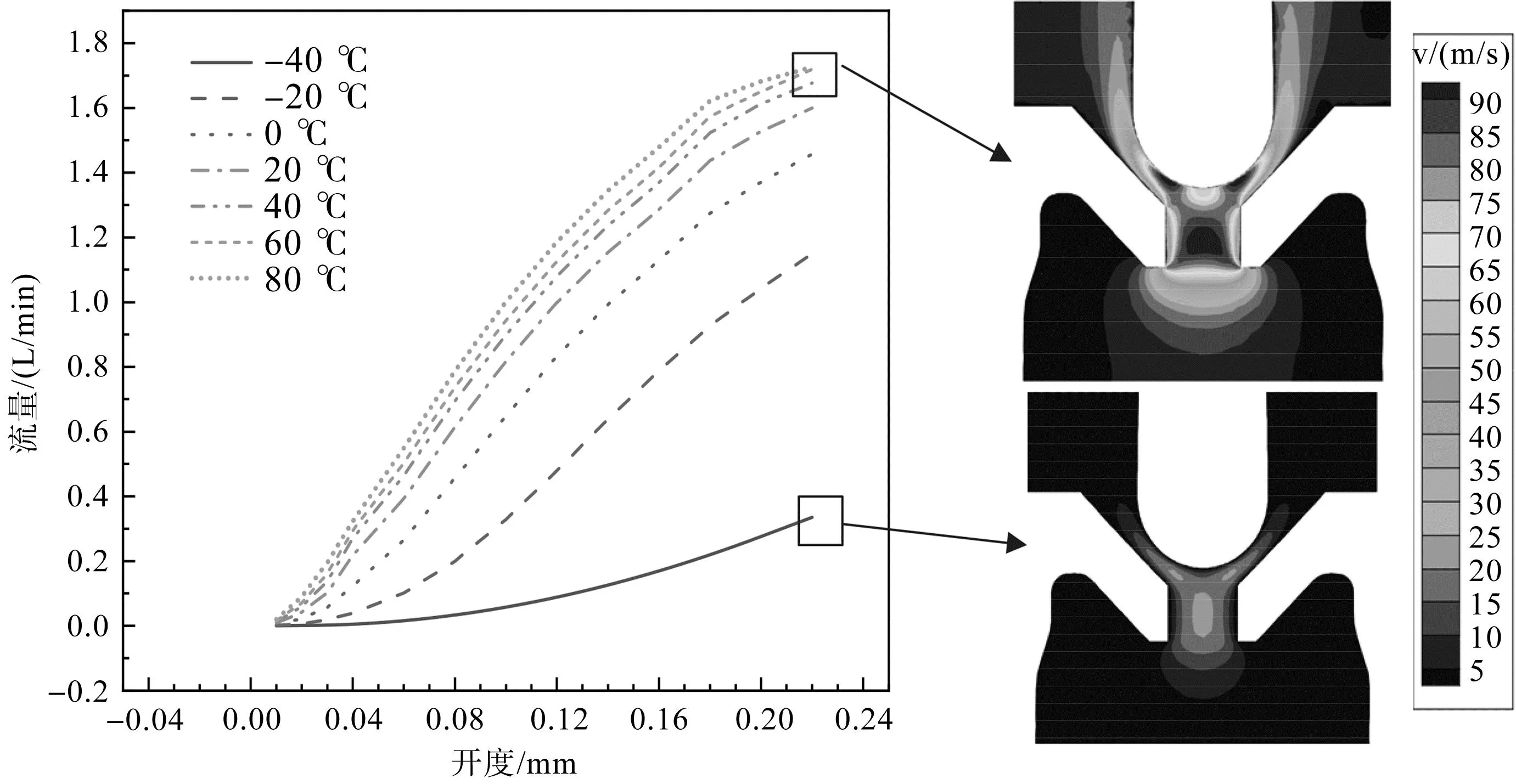
圖17 不同溫度下各開度流量及典型速度云圖Fig.17 Flow rate and typical velocity distribution at various openings and temperatures

圖17左側顯示了不同溫度下,各開度的流量;右側給出了0.22 mm開度下,80 ℃和-40 ℃的速度云圖。

可以看出,在同一開度下,溫度越低,動力黏度越大,液壓油通過閥口速度越小,出口流量越小。

研究表明:流體介質溫度是影響閥芯液壓力的重要因素,低溫對比高溫對液壓力有更大的影響。動力黏度隨溫度的變化與液壓力的變化一致,在低溫下動力黏度的變化較大,從而導致液壓力變化較大。這是因為溫度影響著流體的動力黏度,如圖16所示。在不同溫度下(-40 ℃與-20 ℃之間),液壓油的動力黏度變化了0.67 Pa·s,變化幅度最大。

綜合圖14和圖15可以看出:動力黏度的變化與液壓力變化一致。低溫狀態(tài)下,溫度變化會引起動力黏度的大幅變動,導致液壓力發(fā)生很大變化。高溫狀態(tài)下,溫度對動力黏度影響較小,液壓力變化也很小,液壓油通過閥口速度越大,出口流量越大。

2.5 結構參數對液壓力影響

該節(jié)研究了節(jié)流孔直徑、閥座錐角對液壓力[13]的影響。筆者設定進出口壓差為3 MPa,流體介質溫度為20 ℃。

筆者基于方案二進行仿真計算,結果如表3所示。

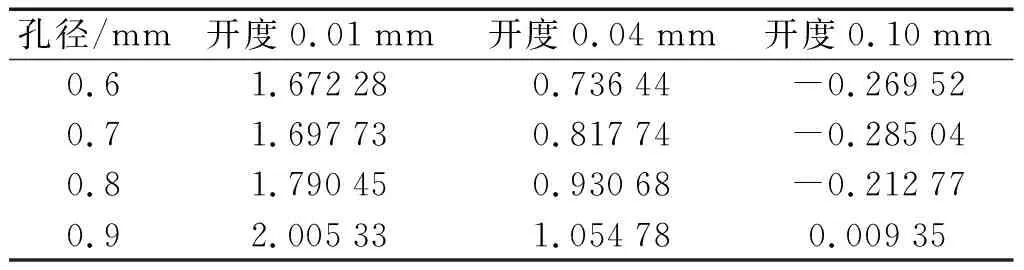
表3 不同直徑閥座節(jié)流孔對應的液壓力Table 3 Hydraulic pressureunder different diameters of the valve seat throttle hole

以一般工作壓差3 MPa為例,筆者選取流體介質溫度為20 ℃,開度為0.01 mm、0.04 mm、0.10 mm,閥座節(jié)流孔直徑為0.7 mm,閥座錐角為60°、70°、80°、90°、120°,進行仿真計算,其結果如表4所示。

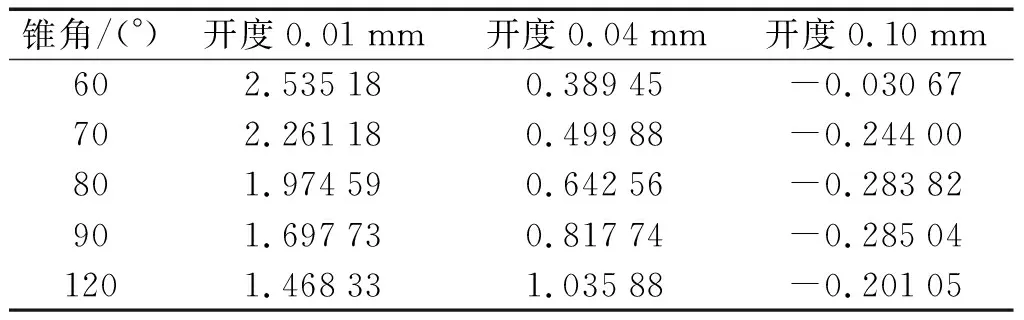
表4 不同閥座錐角對應的液壓力Table 4 Hydraulic pressure under different valve seat cone angles

根據表4數據可以看出:在恒定條件下,閥座節(jié)流孔直徑較大會導致液壓力較高。然而,閥座錐角與液壓力之間的關系未必總是線性的。在同一孔徑和錐角情況下,開度越大,液壓力的數值越小。

但是,在不同的孔徑[14]或者錐角情況下,不同開度,液壓力增幅與變化趨勢各不相同。節(jié)流孔直徑和閥座錐角對液壓力有顯著影響,并且它們之間的關系是非線性的。閥座節(jié)流孔直徑和閥座錐角會同時影響到閉合時閥芯[15]球頭與閥座之間的密封性。

因此,節(jié)流孔直徑和錐角受到物理結構的限制[16-18]。因為節(jié)流孔直徑和閥座錐角對液壓力有顯著影響,所以需對其進行結構參數優(yōu)化。

3 開關閥結構參數優(yōu)化

3.1 設計變量選擇

根據第2節(jié)的分析,閥座節(jié)流孔直徑為P1,閥座錐角為P2時,會對液壓力產生重大影響。因此筆者將它們設為設計變量。

根據電磁閥本身的物理結構,筆者可確定設計變量參數P1、P2的取值范圍。

參數及變化范圍如表5所示。

表5 設計變量及參數變化范圍Table 5 Design variables and parameter ranges

3.2 DOE試驗設計和響應面分析

筆者對設計變量進行中心復合設計(CCD),以閥座節(jié)流孔直徑P1、閥座錐角P2為輸入,液壓力F為輸出,選取9組樣本數進行實驗計算。

樣本點及試驗結果如表6所示。

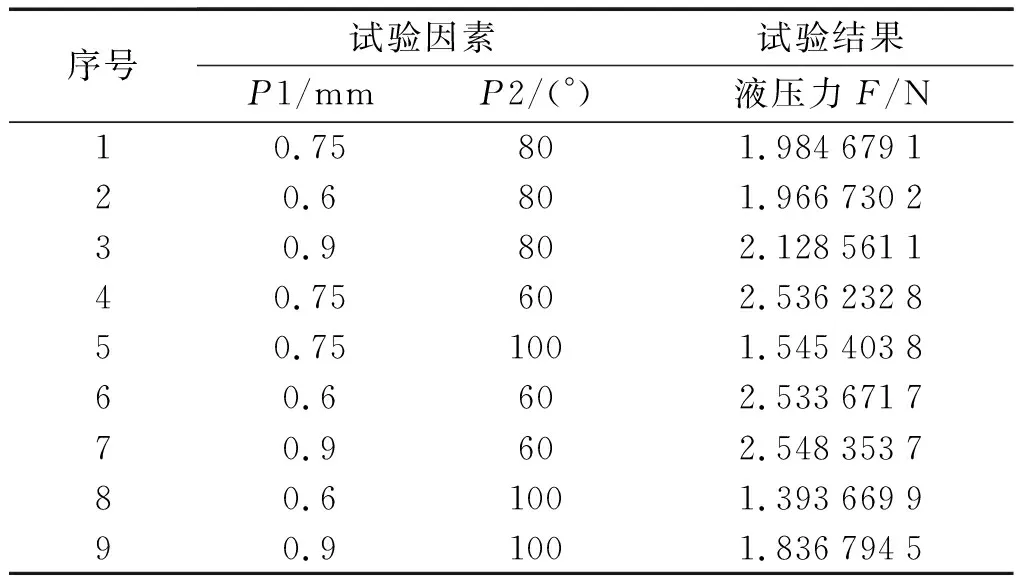
表6 樣本點及試驗結果Table 6 Sample points and experimental results

響應面法[19]結合數理統(tǒng)計原理,采用試驗設計對指定樣本點集合進行試驗分析,得到設計變量的目標函數與約束函數的響應面模型,其可以預測非試驗點的響應值[20-22]。筆者采用遺傳聚合響應面算法,其根據可用的不同類型的響應面(全二階多項式、非參數回歸、克里金法和移動最小二乘法),構建最適合每個輸出參數的響應面類型。

為方便參數化建模,筆者構建閥座半錐角和閥座節(jié)流孔半徑與液壓力的響應面,如圖18所示。

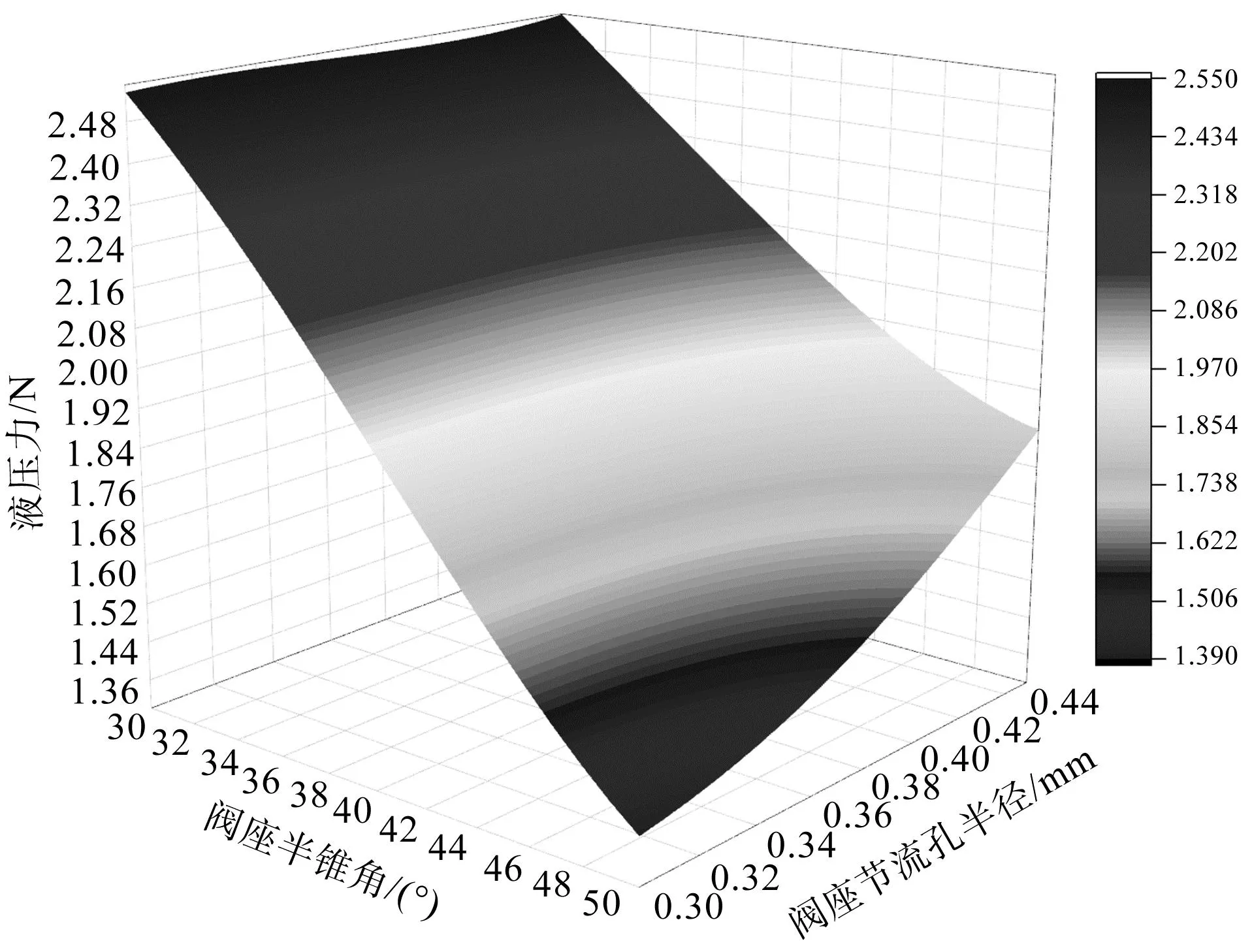
圖18 閥座關鍵參數與液壓力的響應面 Fig.18 Response surface of key seat parameters and hydraulic pressure

從圖18中可以清晰看出閥座半錐角、節(jié)流孔半徑與液壓力三者的關系。

在小節(jié)流孔半徑情況下,隨著閥座錐角的增大,液壓力變小;而對于大節(jié)流孔半徑,隨著閥座錐角的增大,液壓力先變小后變大。

3.3 基于遺傳算法的目標優(yōu)化

在最小開度為0.01 mm時,液壓力越大,液壓力的跨度范圍越大;當液壓力隨開度變化的幅值越大,與其對應的電磁力幅值范圍就越大,控制電流方式的脈寬調制(pulse, width,modulation,PWM)的調控范圍也就越大,從而使調控精度更好[23]。

筆者以0.01 mm開度的液壓力最大為優(yōu)化目標,使用遺傳算法進行優(yōu)化求解。經求解得到三組最優(yōu)解。筆者對這三組解進行仿真驗算,將結果與遺傳算法所得最優(yōu)解進行對比驗證。

計算所得最優(yōu)解集如表7所示[24-26]。

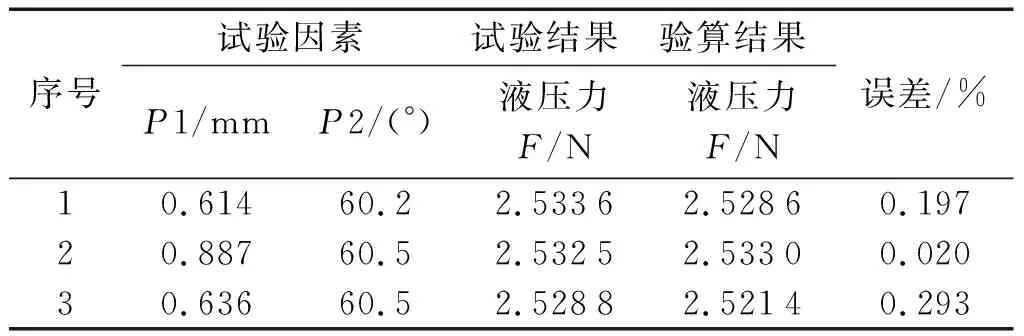
表7 最佳優(yōu)化解集Table 7 Optimal solution set

經過筆者驗證,優(yōu)化的結果與仿真驗算的結果誤差均小于0.3%。

考慮實際加工工藝要求與制造成本,筆者選取閥座節(jié)流孔直徑為0.62 mm,閥座錐角為60°。

優(yōu)化前,閥座節(jié)流孔直徑為0.7 mm,閥座錐角為90°,液壓力為1.697 73 N;優(yōu)化后,節(jié)流孔直徑為0.62 mm,閥座錐角選取60°,液壓力為2.533 N,比優(yōu)化前提高了49.2%。

4 結束語

為了研究不同參數對高速開關閥液壓力的影響,筆者首先建立了不同開度、壓差、溫度,以及結構參數的仿真模型;然后,詳細分析了各參數對液壓力的影響;最后,采用了響應面分析,并結合遺傳算法對開關閥的結構參數進行了優(yōu)化。

研究結論如下:

1)隨著閥口開度的變大,主要節(jié)流區(qū)域發(fā)生了改變。在閥口開度逐漸增加的過程中,首先是閥口起主導節(jié)流作用,但當開度增加到0.18 mm左右時,閥座節(jié)流孔開始起主導節(jié)流作用。高速開關閥進出口兩端壓差越大,液壓力變化幅度越大,閥芯可控開度范圍越小;

2)高溫對液壓力影響較小,而低溫對液壓力有很大影響,這取決于流體介質的動力黏度變化。在低溫之間,動力黏度變化幅度可達85%,動力黏度的大幅變動會導致液壓力劇烈變化。而高溫之間,動力黏度變化幅度在28%左右,溫度的改變不會引起動力黏度的大幅變化,液壓力變動也很小;

3)閥座節(jié)流孔直徑和閥座錐角對液壓力有很大影響,且這種影響是無序的。對閥座節(jié)流孔直徑和閥座錐角兩個結構參數進行了優(yōu)化,可以擴大與液壓力匹配的電磁力范圍。優(yōu)化后,節(jié)流孔直徑為0.62 mm,閥座錐角為60°,電磁力范圍擴大了49.2%。

當前,筆者的研究主要聚焦于閥芯液壓力,暫未考慮電磁鐵結構的問題。在后續(xù)的工作中,筆者會考慮增大液壓力對電磁鐵功率和尺寸的影響,并對高速開關閥的動態(tài)特性進行研究。