基于聚類和隨機搜索優(yōu)化的核反應(yīng)堆數(shù)字孿生參數(shù)反演模型

龍家雨,宋美琪,*,柴 翔,劉曉晶,妥艷潔,3

(1.上海交通大學(xué) 智慧能源創(chuàng)新學(xué)院,上海 200240;2.上海交通大學(xué) 機械與動力工程學(xué)院,上海 200240;3.國家電力投資集團有限公司,北京 100029)

數(shù)字孿生(digital twin)是以數(shù)字化方式創(chuàng)建物理實體的虛擬模型,充分利用物理模型、傳感器、運行歷史等數(shù)據(jù),集成多學(xué)科、多尺度對物理實體在現(xiàn)實環(huán)境中的行為進行模擬的仿真過程。作為虛擬空間中對實體產(chǎn)品的鏡像,其反映了相對應(yīng)物理實體產(chǎn)品的全生命周期過程[1-2]。核電數(shù)字孿生有利于核電站以較低成本實現(xiàn)高可靠性、可用性與可維護性[3],可在核電站的預(yù)測性運行與維護、自主運行與控制等領(lǐng)域發(fā)揮作用,如實現(xiàn)小型模塊化反應(yīng)堆自動、自主和實時性能要求[4]或結(jié)合先進PSA(概率風(fēng)險評估)方法構(gòu)建實時決策支持系統(tǒng)[5]等。

核電站為實時監(jiān)測運行狀態(tài)而布置大量的傳感器,產(chǎn)生的數(shù)據(jù)種類多、總量大,造成存儲空間需求大、傳輸效率不高、數(shù)據(jù)分析復(fù)雜度高等問題,基于核電站構(gòu)建的數(shù)字孿生系統(tǒng)同樣面臨此類問題,如何優(yōu)化傳感器的布置也需要進一步研究。核電領(lǐng)域常采用數(shù)據(jù)降維與反向求解的特征工程進行數(shù)據(jù)處理與分析[6-7]。Peng等[8]利用稀疏自動編碼器(sparse auto encoder)對仿真程序PCTRAN模擬的核電站的幾種不同瞬態(tài)參數(shù)提取特征,實現(xiàn)對核電站異常狀態(tài)的檢測。Yang等[9]用一維卷積神經(jīng)網(wǎng)絡(luò)(CNN)重建核電站傳感器信號,通過逐步減少傳感器進行實驗,在16種傳感器數(shù)據(jù)確定了5種影響最大的參數(shù)。李翔宇等[10]通過改進特征工程算法建立了一種核電站瞬態(tài)運行參數(shù)數(shù)據(jù)壓縮和數(shù)據(jù)復(fù)原方法,結(jié)合主成分分析法與高斯回歸過程方法對秦山300 MWe全范圍仿真機產(chǎn)生的瞬態(tài)運行數(shù)據(jù)進行壓縮與高精度復(fù)原。

目前此類研究在特征提取上面臨如下的問題:通過逐次實驗的方式獲取特征參數(shù),依賴長期數(shù)據(jù),運算量大、效率較低;采用主成分分析等方式進行數(shù)據(jù)壓縮,在壓縮過程中改變了原參數(shù)的值,雖然提升了傳輸效率且能達到很高精度,但也因此失去了特征參數(shù)的可解釋性。

針對上述問題,本文基于多物理場耦合程序?qū)崿F(xiàn)空間熱離子反應(yīng)堆虛擬模型的構(gòu)建并獲取數(shù)字孿生數(shù)據(jù),結(jié)合K-means聚類算法與ANN(人工神經(jīng)網(wǎng)絡(luò)),提出一種能夠在保留原數(shù)據(jù)的情況下高效提取特征參數(shù)并對其他非特征參數(shù)進行反演的方法,對空間熱離子反應(yīng)堆堆芯的4個區(qū)域的溫度參數(shù)分別建立參數(shù)反演模型并取得較高精度的反演結(jié)果。

1 數(shù)據(jù)集建立

本文的參數(shù)反演模型是對空間熱離子反應(yīng)堆的數(shù)字孿生堆芯溫度數(shù)據(jù)建立的。對堆芯物理系統(tǒng)的數(shù)字孿生計算通過上海交通大學(xué)搭建的多物理場耦合數(shù)值模擬平臺[11]完成。

1.1 空間熱離子堆堆芯系統(tǒng)

與常規(guī)壓水堆相比,空間熱離子反應(yīng)堆體形較小,堆芯三維幾何模型如圖1所示。空間熱離子反應(yīng)堆由37根熱離子燃料元件和ZrH慢化劑芯塊組成。通過旋轉(zhuǎn)控制鼓引入反應(yīng)性,從而啟動空間熱離子反應(yīng)堆。燃料熱量產(chǎn)生與傳遞過程如下:燃料芯塊發(fā)生核裂變反應(yīng),產(chǎn)生熱量,熱量通過發(fā)射極、接收極、氣隙傳遞給冷卻劑,冷卻劑通過對流換熱將會帶走部分熱量,剩余熱量傳遞給慢化劑芯塊,慢化劑通過熱輻射向太空散失部分熱量。

圖1 空間熱離子反應(yīng)堆堆芯的幾何模型[11]Fig.1 Geometric model of space thermionic reactor core[11]

空間熱離子反應(yīng)堆堆芯中最核心的部件是熱離子燃料元件,其結(jié)構(gòu)示于圖2。熱離子燃料元件為單節(jié)全長多層套筒結(jié)構(gòu)的熱離子燃料元件,采用高濃縮UO2作為燃料,NaK-78作為冷卻劑。發(fā)射極材料為單晶鉬和化學(xué)氣相沉積制成的鎢表面層,接收極由多晶鉬制成,接收極外包有Al2O3絕緣體薄層。

圖2 單節(jié)熱離子燃料元件[11]Fig.2 Single-section thermionic fuel element[11]

1.2 數(shù)據(jù)獲取

使用基于OpenFOAM開發(fā)的多物理場耦合程序?qū)臻g熱離子反應(yīng)堆構(gòu)建數(shù)值模擬平臺。網(wǎng)格劃分、工況設(shè)置、相關(guān)方程及計算可見文獻[11]。基本參數(shù)的程序計算值與設(shè)計值吻合良好,在設(shè)計范圍內(nèi)。

20%熱管失效工況下的仿真結(jié)果中包含燃料、發(fā)射極、接收極、冷卻劑4個區(qū)域的溫度計算結(jié)果,采樣時間間隔為0.1 s,瞬態(tài)計算從750 s開始到2 425 s結(jié)束,共16 750個時間節(jié)點。沿燃料元件軸向(z軸)均勻分布的100個測點,高度從0到0.375 m。剔除最初原始數(shù)據(jù)發(fā)生突變的時間點,最終生成了16 748×1 601維的數(shù)據(jù)集,對應(yīng)1 600個參數(shù)的16 748個時間節(jié)點。

用相同的方式獲取15%熱管失效工況下的堆芯溫度數(shù)據(jù),包含從750.2 s到1 893.9 s共11 438個時間節(jié)點,參數(shù)種類與20%熱管失效工況下的相同,將用于參數(shù)反演模型的效果驗證。

2 參數(shù)反演模型構(gòu)建

本文構(gòu)建的參數(shù)反演模型結(jié)構(gòu)如圖3所示。不同于自動編碼器與數(shù)據(jù)壓縮復(fù)原方法,本文構(gòu)建的模型在特征提取環(huán)節(jié)通過機器學(xué)習(xí)方法快速選取出特征參數(shù)并且保留了其原始數(shù)據(jù)。

圖3 本文的參數(shù)反演模型Fig.3 Parameter inversion model proposed in this paper

依據(jù)如圖4所示流程構(gòu)建參數(shù)反演模型,包括特征提取與神經(jīng)網(wǎng)絡(luò)搭建兩部分,并在最后進行模型效果驗證。

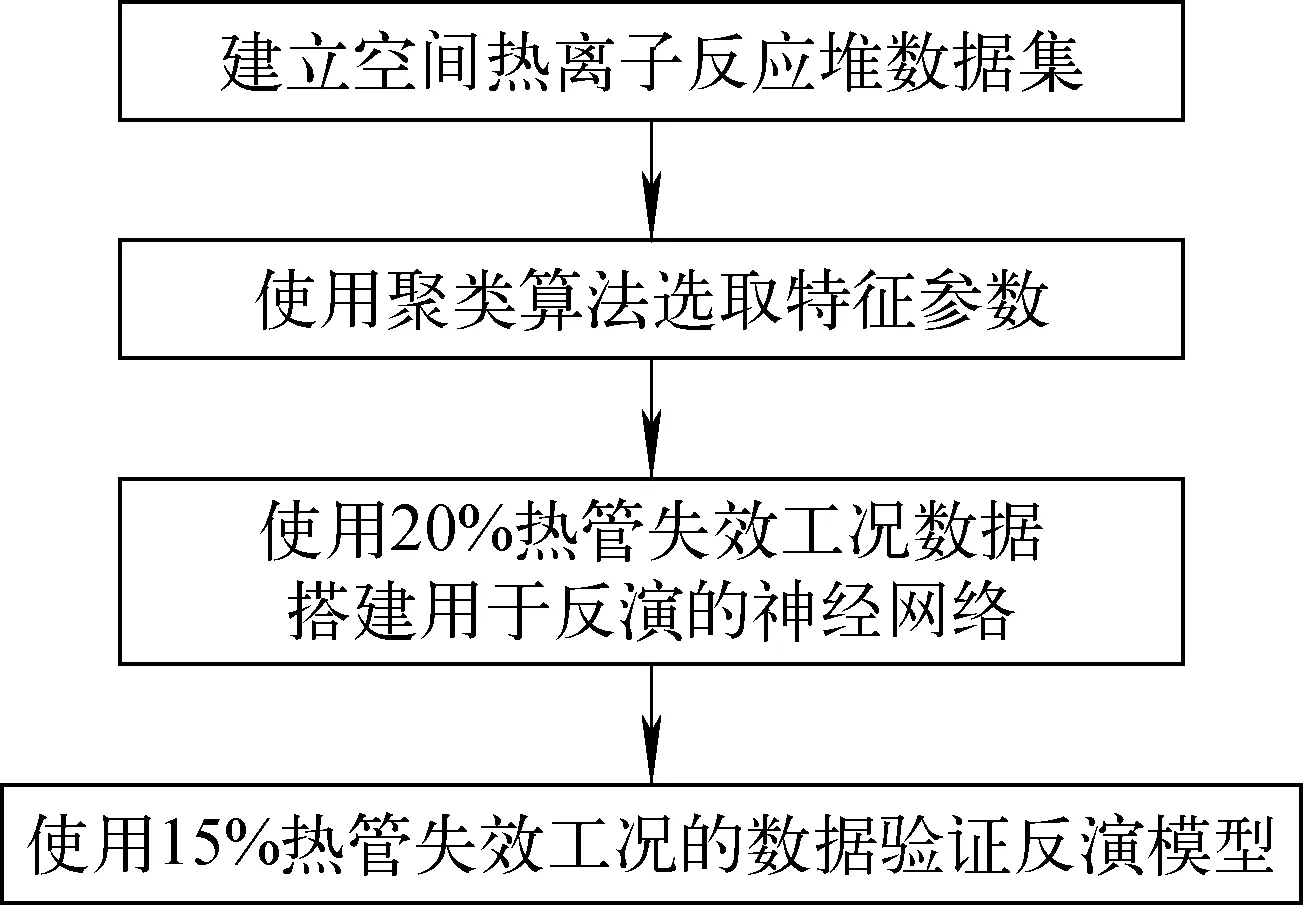
圖4 參數(shù)反演模型搭建流程Fig.4 Process of constructing parameter inversion model

2.1 基于K-means的特征選取環(huán)節(jié)

特征選取是一個數(shù)據(jù)降維環(huán)節(jié),將原始數(shù)據(jù)轉(zhuǎn)換為低維度的特征向量,從而提高數(shù)據(jù)傳輸與分析效率,也節(jié)約了存儲空間。K均值聚類算法(K-means算法)是一種無監(jiān)督的分類方法,在設(shè)定聚類數(shù)后可自動通過算法完成不同參數(shù)類別的劃分。不同類簇中的中心參數(shù)表征了該類參數(shù)中的典型值,選擇到聚類中心有最小平方歐氏距離的參數(shù)作為特征參數(shù)。由此,通過K-means聚類可以高效選取特征參數(shù)。聚類數(shù)的選擇影響著聚類最終效果的好壞,選擇輪廓系數(shù)(silhouette coefficient)作為評估聚類效果的指標,并比較不同聚類數(shù)的輪廓系數(shù)以選擇最佳聚類數(shù)。

特征選取環(huán)節(jié)包括如下步驟:將空間熱離子反應(yīng)堆的數(shù)字孿生數(shù)據(jù)歸一化、使用K-means算法分類、使用輪廓系數(shù)指標評估聚類效果、提取各類最接近聚類中心的參數(shù)作為特征參數(shù),流程如圖5所示。

圖5 特征提取流程Fig.5 Process of feature extraction

首先,分別對4個位置的溫度參數(shù)進行歸一化處理,將數(shù)據(jù)映射到[0,1]之間。使用如下公式:

(1)

K-means算法的核心思想是找出K個聚類中心c1,c2,…,cK,使得每個數(shù)據(jù)點xi和與其最近的聚類中心cv的平方距離和被最小化(該平方距離和被稱為偏差D)[12],主要步驟[13]如下。

1) 聚類中心初始化:隨機指定K個聚類中心c1,c2,…,cK。

2) 對樣本歸類:每個樣本xi僅選擇1個聚類中心S(t)作為歸屬,找到與它具有最小平方歐氏距離的聚類中心cv,并將其分配到所標明的類cv:

?n,1≤n≤K}

(2)

3) 更新聚類中心cn:將每個cn移動到其標明的類的中心:

(3)

4) 計算偏差D:

(4)

5) 判斷偏差D是否收斂:如果D收斂,則返回c1,c2,…,cK并終止本算法;否則,返回步驟2。

輪廓系數(shù)是用來評估聚類效果好壞的一種指標,衡量聚類中樣本的內(nèi)聚度和分離度。內(nèi)聚度ai為第i個樣本到同簇中其他點的距離的平均值,分離度bi為第i個樣本到其他簇中點的距離的平均值,第i個樣本的輪廓系數(shù)[14]為:

(5)

式中:Si越接近1,說明樣本i的聚類合理;Si為0時,說明樣本i處于兩簇的邊界;Si為-1時,說明樣本i應(yīng)該被分到其他的簇。對所有樣本的輪廓系數(shù)取平均值,得到聚類結(jié)果的總輪廓系數(shù)。

以接收極為例,輪廓系數(shù)隨聚類數(shù)的變化如圖6所示。在聚類數(shù)為31時,輪廓系數(shù)達到最大,表明類數(shù)選為31類時的聚類效果最好。

圖6 接收極的輪廓系數(shù)隨聚類數(shù)的變化Fig.6 Variation of silhouette coefficient of receiving pole with number of clusters

確定聚類數(shù)后,選取每類中到聚類中心平均距離最小的參數(shù)曲線作為特征參數(shù),保存特征索引。參數(shù)索引與幾何位置一一對應(yīng),其中軸向方向序號z-1～z-100分別代表0.003 75 m的整數(shù)倍,如z-3代表軸向0.003 75 m×3處位置;徑向方向序號r-1代表徑向中心處,r-2、r-3、r-4分別代表3個不同徑向位點。仍以接收極為例,提取的31個特征參數(shù)的對應(yīng)位點列于表1。

從表1可看出,特征參數(shù)沿軸向分布較為均勻,在徑向分布上,位于中心與4號徑向位點的特征參數(shù)占所有特征參數(shù)的74.2%,表明這兩個徑向位點的參數(shù)值得關(guān)注。由于上述特征參數(shù)均可在堆芯中確定其所屬位置,因此也可確認每個特征參數(shù)的含義。

對各區(qū)域分別進行聚類,4個區(qū)域的聚類數(shù)最終確定如表2所列。重復(fù)上述流程,得到4個區(qū)域的特征參數(shù)及其對應(yīng)的位點信息。將特征參數(shù)與非特征參數(shù)重新編排為新的數(shù)據(jù)集,用于下一步的參數(shù)反演。

表2 不同區(qū)域的聚類數(shù)Table 2 Clusteringnumbers of different regions

2.2 搭建神經(jīng)網(wǎng)絡(luò)反演模型

完成對數(shù)據(jù)的降維后,需要進行反向求解,通過使用降維后的數(shù)據(jù)求出對應(yīng)的物理場分布與相應(yīng)探測器的理論測量值,從而完成數(shù)據(jù)的反演。本文為4個區(qū)域分別搭建全連接神經(jīng)網(wǎng)絡(luò)進行參數(shù)反演,并使用隨機配置法優(yōu)化神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)和學(xué)習(xí)率,根據(jù)各區(qū)域的反演結(jié)果評估參數(shù)反演模型。

神經(jīng)網(wǎng)絡(luò)的計算單元完成輸入xi與權(quán)重wi的加權(quán)求和,添加偏置bi并經(jīng)過激活函數(shù)Φ得到輸出yi,構(gòu)成下一層的輸入或者最終的輸出[15],如下式:

(6)

全連接代表每個神經(jīng)元與相鄰層的所有神經(jīng)元相連,且同層中的神經(jīng)元互不連接。選擇MSE(均方差)作為損失函數(shù),以歐氏距離表達反演的預(yù)測值yi與真實值y′i的距離:

(7)

使用SGD(隨機梯度下降)函數(shù),通過反向傳播更新神經(jīng)網(wǎng)絡(luò)權(quán)值,每個連接的權(quán)值通過自身減去學(xué)習(xí)率與損失函數(shù)對該權(quán)值的一階偏導(dǎo)數(shù)進行更新。使用原始數(shù)據(jù)輸入神經(jīng)網(wǎng)絡(luò),溫度值的范圍在[750 ℃,2 500 ℃],由此選擇神經(jīng)網(wǎng)絡(luò)各隱藏層的激活函數(shù)為Leaky-ReLU。將16 748個時間節(jié)點數(shù)據(jù)按12 000∶2 000∶2 748的比例劃分為訓(xùn)練集、驗證集、測試集,在前14 000個時間節(jié)點中按照12 000∶2 000的比例隨機劃分為訓(xùn)練集與驗證集。收斂條件設(shè)置為兩輪MSE之差小于1×10-6且MSE<100。以接收極為例,初步搭建神經(jīng)網(wǎng)絡(luò)。經(jīng)嘗試,當學(xué)習(xí)率大于1×10-7時訓(xùn)練易發(fā)散。采用1×10-7的學(xué)習(xí)率、網(wǎng)絡(luò)結(jié)構(gòu)為3層、每層各20個節(jié)點的全連接神經(jīng)網(wǎng)絡(luò),設(shè)置1 500輪訓(xùn)練。損失隨迭代輪數(shù)的變化如圖7所示,最終訓(xùn)練集與驗證集損失分別為0.716 4和0.844 8。然后圍繞上述參數(shù),對學(xué)習(xí)率、神經(jīng)網(wǎng)絡(luò)層數(shù)與節(jié)點數(shù)進行優(yōu)化。

圖7 訓(xùn)練損失與驗證損失隨迭代次數(shù)的變化Fig.7 Variation of training loss and validation loss with number of iterations

對神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)的優(yōu)化方法包括試驗法、窮舉法、啟發(fā)式算法、修剪與構(gòu)造算法等[16],其中能夠自動搜索來完成的有隨機配置法、系統(tǒng)化搜索、窮舉法、啟發(fā)式方法。本文使用隨機配置法選取神經(jīng)網(wǎng)絡(luò)的隱藏層層數(shù)及各層節(jié)點數(shù)、學(xué)習(xí)率。4個區(qū)域各自的神經(jīng)網(wǎng)絡(luò)在初步訓(xùn)練后實現(xiàn)收斂,圍繞初步訓(xùn)練的神經(jīng)網(wǎng)絡(luò)參數(shù)進行配置,為4個區(qū)域的隱藏層數(shù)、各層節(jié)點數(shù)、學(xué)習(xí)率設(shè)定搜索區(qū)間進行隨機配置。

根據(jù)Robert Hecht Nielson的證明,1個3層的BP網(wǎng)絡(luò)可以完成任意M維到m維的映射[17]。考慮到堆芯溫度數(shù)據(jù)的輸入維度遠小于輸出維度,將隱藏層數(shù)的選擇范圍設(shè)定為2～5。

隱藏層節(jié)點數(shù)的選取具有高度任意性,節(jié)點數(shù)的范圍參照如下經(jīng)驗公式[18]并適當擴大范圍:

(8)

式中:n1為隱藏層節(jié)點數(shù);n為該層的輸入神經(jīng)元數(shù);m為該層的輸出神經(jīng)元數(shù);a為1～10之間的常數(shù)。節(jié)點搜索范圍確定為[5,25]或[5,30]。

根據(jù)初步訓(xùn)練的配置,將學(xué)習(xí)率的搜索范圍設(shè)為[1×10-9,1×10-7]。各區(qū)域的神經(jīng)網(wǎng)絡(luò)參數(shù)搜索范圍列于表3。最大輪數(shù)設(shè)置為20 000,滿足收斂條件時結(jié)束。

表3 不同區(qū)域的神經(jīng)網(wǎng)絡(luò)參數(shù)配置隨機搜索區(qū)間Table 3 Random search interval of neural network parameter configuration for different regions

神經(jīng)網(wǎng)絡(luò)訓(xùn)練與優(yōu)化流程如圖8所示。

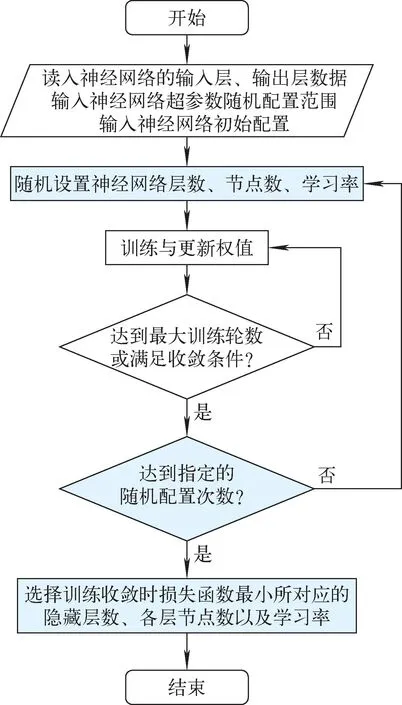
圖8 神經(jīng)網(wǎng)絡(luò)訓(xùn)練與優(yōu)化流程Fig.8 Neural network training and optimization process

對各區(qū)域分別設(shè)置30種隨機組合,綜合考慮訓(xùn)練集收斂速度最快、收斂時MSE最小的組合作為神經(jīng)網(wǎng)絡(luò)配置。當收斂輪數(shù)與最終訓(xùn)練損失不能同時達到最小時,選擇相近的訓(xùn)練損失中收斂輪數(shù)最小的作為配置。以發(fā)射極為例,從30種配置結(jié)果中選出損失最小的5組,如表4所列。從中可以看出,組別為4號的配置具有最小的最終訓(xùn)練損失與最快的收斂速度,故作為最后的神經(jīng)網(wǎng)絡(luò)配置,訓(xùn)練損失變化如圖9所示。

表4 發(fā)射極訓(xùn)練損失最小的幾組配置Table 4 Several configurations of minimal training loss in emitter

圖9 發(fā)射極神經(jīng)網(wǎng)絡(luò)最終配置下的訓(xùn)練損失變化Fig.9 Training loss variation of emitter neural network with final configuration

通過上述流程獲得4個區(qū)域的不同神經(jīng)網(wǎng)絡(luò)配置,結(jié)果列于表5。

3 反演結(jié)果

對反演值與實際數(shù)值進行比較,采用如下方式:對角線圖能直觀地比較反演值與實際值;相對誤差頻數(shù)分布直方圖展示不同誤差區(qū)間的數(shù)據(jù)數(shù)目;相對誤差的RMSE(均方根誤差)反映了反演的總體誤差,計算方法為:

(9)

將上述訓(xùn)練好的神經(jīng)網(wǎng)絡(luò)用于15%熱管失效工況下的堆芯溫度數(shù)據(jù),各部分的反演結(jié)果如下。

3.1 燃料溫度反演結(jié)果

燃料溫度范圍在[1 370 ℃, 2 450 ℃]。燃料溫度的反演值與真實值貼近直線y=x(圖10),相對誤差分布如圖11所示。最大相對誤差在±1.4%內(nèi),94.34%的數(shù)據(jù)反演值相對誤差在1%以內(nèi),相對誤差均方根不超過0.6%。

圖10 燃料溫度的反演值與真實值對角線圖Fig.10 Diagonals of inverse and actual values of fuel temperature

圖11 燃料溫度相對誤差頻數(shù)分布直方圖Fig.11 Relative error frequency distribution histogram of fuel temperature

3.2 發(fā)射極溫度反演結(jié)果

發(fā)射極溫度范圍在[1 350 ℃, 2 220 ℃]。發(fā)射極溫度的反演值與真實值的對角線圖如圖12所示,相對誤差分布如圖13所示。最大相對誤差不超過1.2%,相對誤差均方根在0.4%左右。整體誤差較燃料更小。

圖12 發(fā)射極溫度的反演值與真實值對角線圖Fig.12 Diagonals of inverse and actual values of emitter temperature

圖13 發(fā)射極溫度相對誤差頻數(shù)分布直方圖Fig.13 Relative error frequency distribution histogram of emitter temperature

3.3 接收極溫度反演結(jié)果

接收極溫度范圍在[750 ℃, 935 ℃]。接收極溫度的反演值與真實值的對角線圖如圖14所示,誤差分布如圖15所示。99.75%的反演值相對誤差不超過0.6%,相對誤差均方根不超過0.2%。

圖14 接收極溫度的反演值與真實值對角線圖Fig.14 Diagonals of inverse and actual values of receiving pole temperature

圖15 接收極溫度相對誤差頻數(shù)分布直方圖Fig.15 Relative error frequency distribution histogram of receiving pole temperature

3.4 冷卻劑溫度反演結(jié)果

冷卻劑溫度范圍在[730 ℃, 920 ℃]。冷卻劑溫度的反演值與真實值的對角線圖如圖16所示,相對誤差分布如圖17所示。92.09%的反演值相對誤差在±0.3%以內(nèi),98.67%的反演值相對誤差在[-0.3%,0.9%],相對誤差均方根不超過0.2%。

圖16 冷卻劑溫度的反演值與真實值對角線圖Fig.16 Diagonals of inverse and actual values of coolant temperature

4 結(jié)論

本文在當前相關(guān)研究無法同時兼顧特征參數(shù)的自動、高效選取與保留特征參數(shù)的可解釋性的情況下,基于多物理場耦合程序構(gòu)建空間熱離子反應(yīng)堆的數(shù)字孿生,結(jié)合聚類算法與隨機搜索優(yōu)化的人工神經(jīng)網(wǎng)絡(luò)對20%熱管失效工況下的堆芯溫度建立了溫度參數(shù)反演模型,并通過15%熱管失效工況數(shù)據(jù)進行反演效果驗證。結(jié)果表明,運用本文流程搭建的參數(shù)反演模型,對于空間熱離子反應(yīng)堆堆芯各區(qū)域的溫度參數(shù),反演最大相對誤差在1%上下,相對誤差均方根在0.001 8～0.005 5之間;能實現(xiàn)參數(shù)比例小于1∶10的反演,對空間熱離子反應(yīng)堆堆芯溫度場的反演取得良好的精度,提高傳輸、儲存與分析效率;且獲取的特征參數(shù)可通過索引定位到不同構(gòu)件/區(qū)域的軸向與徑向位置,從而得到特征參數(shù)的物理意義。本研究的模型可以拓展應(yīng)用到空間熱離子反應(yīng)堆其他區(qū)域以及其他堆型,高效獲取特定區(qū)域的特征參數(shù)并保留特征參數(shù)的位置信息,為未來小型堆探測器的安裝提供依據(jù),也為研究大規(guī)模的核電數(shù)據(jù)提供了一種可行思路。