關(guān)于n-純同調(diào)維數(shù)的注記

呂家鳳, 金欣怡

(1.浙江師范大學(xué) 數(shù)學(xué)科學(xué)學(xué)院,浙江 金華 321004;2.浙江師范大學(xué) 初陽(yáng)學(xué)院,浙江 金華 321004)

0 引 言

自20世紀(jì)六七十年代純模與純正合列的概念提出后,其性質(zhì)引起了廣泛關(guān)注.值得注意的是,純正合列的定義是基于有限表現(xiàn)模的.為了研究諾特環(huán)、凝聚環(huán)以及更一般環(huán)上的同調(diào)性質(zhì),模的有限表現(xiàn)性的研究越來(lái)越受到人們的關(guān)注[1-5].例如,Bravo等[4]建立了n-凝聚環(huán)與n-表現(xiàn)模之間的聯(lián)系,并研究了其同調(diào)性質(zhì).設(shè)n為非負(fù)整數(shù),如果存在一個(gè)正合列Pn→Pn-1→…→P1→P0→M→0,使得每個(gè)Pi都是有限生成的投射模,那么稱一個(gè)模M為n-表現(xiàn)的[2].易見,0-表現(xiàn)模是有限生成的,1-表現(xiàn)模即為有限表現(xiàn)模,每個(gè)(n+1)-表現(xiàn)模是n-表現(xiàn)的.反之不成立,文獻(xiàn)[3]給出了反例.最近,為了研究n-純導(dǎo)出范疇的同調(diào)性質(zhì),文獻(xiàn)[5]引入了n-純正合列、n-純投射模以及n-純內(nèi)射模等概念.受此啟發(fā),本文運(yùn)用同調(diào)的方法,研究了模與環(huán)的n-純投射維數(shù)與n-純內(nèi)射維數(shù),并證明了環(huán)R的n-純投射整體維數(shù)不超過(guò)1的充分必要條件是R的n-純內(nèi)射整體維數(shù)不超過(guò)1.

本文中,環(huán)R指的是含單位元的結(jié)合環(huán),除特別說(shuō)明外,R-模表示的是左R-模,m與n均為非負(fù)整數(shù).其他未說(shuō)明的概念與術(shù)語(yǔ)參見文獻(xiàn)[6-8].

1 預(yù)備知識(shí)

定義1若對(duì)任意n-表現(xiàn)模M,有正合列

0→HomR(M,A)→HomR(M,B)→HomR(M,C)→0,

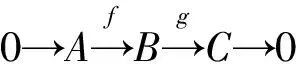
定義2設(shè)M為R-模,若對(duì)任意n-純正合列0→A→B→C→0,都有正合列

0→HomR(M,A)→HomR(M,B)→HomR(M,C)→0,

則稱M為n-純投射模.類似地,若對(duì)任意n-純正合列0→A→B→C→0,都有正合列

0→HomR(C,M)→HomR(B,M)→HomR(A,M)→0,

則稱M為n-純內(nèi)射模.

以下分別用PPn與PIn表示所有n-純投射模與n-純內(nèi)射模.

命題1[5]設(shè)η：0→A→B→C→0為R-模正合列,則下列條件等價(jià)：

1)η是n-純正合列;

2)對(duì)……