求解分裂可行問題的次梯度投影松弛算法

陳進作, 王元恒

(浙江師范大學 數學科學學院,浙江 金華 321004)

0 引 言

分裂可行問題[1]自提出以來,得到越來越多學者的關注[2-8],并且在信息[2]、醫療[3]等領域得到了廣泛應用.分裂可行問題的數學模型是

尋找x∈C使得Ax∈Q.

(1)

式(1)中：C,Q分別為Hilbert空間H1與H2的非空閉凸集;A是有界線性算子.Byrne[3]提出CQ算法,

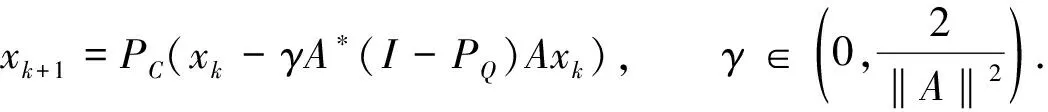
(2)

式(2)中：PC是空間H1在C上的投影算子;PQ是空間H2在Q上的投影算子;I是恒等算子.后續的算法研究多數是在CQ算法基礎上的完善與改進,其中有較大影響的是Yang[4]提出的建立在半空間上的松弛CQ算法,

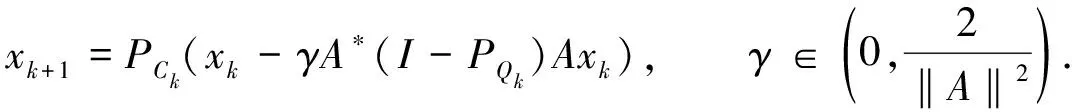
(3)

式(3)中：Ck是C與一族半空間的交集;Qk是Q與一族半空間的交集.相對非空閉凸集C與Q,半空間上投影的計算更加簡單.注意到CQ算法(2)與松弛CQ算法(3)中的步長依賴于算子范數‖A‖,Lpez等[5]提出自適應步長,改進了松弛CQ算法,

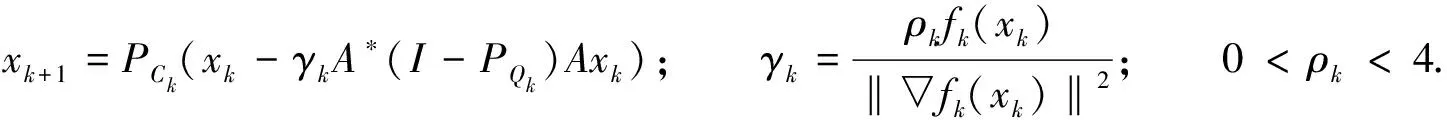
(4)

注意到算法(2)～算法(4)中的投影都是正交投影,本文提出次梯度投影算法求解分裂可行問題.

1 預備知識

定義次梯度投影,需要以下概念及命題：

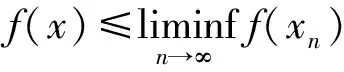
定義2[10]水平集C0={x∈H1|c(x)≤0},其中c：H1→(-∞,+∞]為下半連續凸函數;水平集Q0={y∈H2|q(y)≤0},其中q：H2→(-∞,+∞]為下半連續凸函數.

定義3[10]給定函數f：H1→(-∞,+∞],當

f(y)≥f(x)+〈u,y-x〉,y∈H1

成立時,稱u為f在點x的次梯度.稱f在點x的所有次梯度構成的集合為f在點x的次微分,記為?f(x).

定義4[10]設H為Hilbert空間,給定水平集C0,給定函數f：H→R,取定s(x)∈?f(x),定義關于函數f的次梯度投影為：

G：H→H;

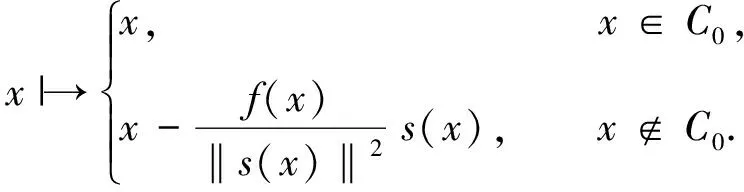
如果f為Gateaux可微,那么關于f的次梯度投影為：

G：H→H;

引理1[6]給定函數f：H1→(-∞,+∞],則f為下半連續凸函數當且僅當f為弱下半連續凸函數.

定義5[8]給定H1中非空閉凸集C,若{xk}?C,則當

‖xk+1-z‖≤‖xk-z‖, ?z∈C

成立時,稱{xk}是Fejer單調的.

引理2[7]若{xk}在C中是Fejer單調的,則{xk}弱收斂于z∈C當且僅當{xk}的每一個弱聚……