不同運動參數對圓筒型FPSO 垂蕩性能和附加質量的影響

余勇軍，王文杰，李 焱，劉利琴

（1.天津大學水利仿真與安全國家重點實驗室，天津 300072；2.大連船舶重工集團有限公司，遼寧 大連 116083）

南海海域油氣資源極其豐富，是我國規模最大的海洋油氣儲存區，據不完全統計，已探明的石油資源有6.4 億噸，天然氣儲量為1 億立方米。FPSO是海洋石油勘探和采集的重要海洋裝備之一，具有投資成本低、適應性強等優勢[1]。較早時期，FPSO大多為舊船改造而成，其細長型結構承受更大的總縱彎曲載荷，可能發生更大的總縱變形。船型結構甲板承載能力較弱，不利于采油作業，且較大的橫搖響應使得正常作業變得很困難。相比之下，圓筒型FPSO 由于其對稱的結構，具有各向同性、無風向標效應[2]且縱搖性能較好，近幾年間獲得了較多關注。

與傳統船型FPSO 相比，圓筒型FPSO 垂蕩阻尼小、垂蕩運動響應大且難以控制[3]，是其走向工程應用亟待解決的一大難題。為此，許多學者嘗試設計和改進圓筒型FPSO 的垂蕩抑制結構來改善其阻尼性能。童波等[4]對比分析了多種不同類型阻尼結構的阻尼性能，結果表明倒U 型阻尼性能最佳。JI X J 等[5]提出了一種帶有錐角的減動結構，研究了不同錐角和孔徑對于圓筒型FPSO 垂蕩性能的影響，發現孔徑在一定程度上能提高阻尼性能。李晨等[6]對比分析了上揚邊鋒型和鋸齒型的減動結構，結果表明鋸齒型減動結構的阻尼效果更優。郝未南等[7]研究了多種垂蕩抑制機構對圓筒型FPSO 阻尼和運動性能的影響，結果同樣證實了鋸齒能顯著影響阻尼性能和流場。陳維等[8]設計了具有通海形式的延伸筒體與減動結構的新型圓筒型FPSO，來解決垂蕩性能差的問題。白杰等[9]提出了一種帶間隙和外板邊鋒垂蕩抑制結構的圓筒型FPSO，并通過模型實驗研究了垂蕩抑制結構對運動性能的影響，結果表明兩者均起到了增加阻尼的作用，而帶外板邊鋒垂蕩抑制結構的阻尼增加效果最顯著。

本文基于CFD 的方法對帶減動結構的圓筒型FPSO 進行數值模擬，建立三維數值水池模型，進行網格無關性和時間步長穩定性驗證，通過用戶自定義函數（User Defined Function，UDF）模擬FPSO發生強迫垂蕩運動的方式計算得到垂蕩阻尼和附加質量，進而探究不同運動周期和幅值下的圓筒型FPSO 的垂蕩阻尼和附加質量變化規律。

1 理論方法

本文基于CFD 方法，采用Fluent 軟件進行數值模擬，本節簡要介紹了流體基本控制方程、流體體積法、湍流模型和阻尼、附加質量的計算方法等內容。

1.1 基本控制方程

流體的連續方程和動量方程共同組成了流體運動的基本控制方程（Navier-Stokes 方程），即N-S方程。考慮非定常、不可壓縮流體，方程可寫為如下分量形式。

式中，u、v、w分別為x、y、z方向上的速度分量；ρ為流體的密度；p為流體微元所受的壓力；v為流體運動黏滯系數。

對于大多數流動問題而言，體積力一般為重力，則有gx=gy=0 和gz=-g。其中，g 為重力加速度。

1.2 流體體積法

海洋結構物數值模擬通常涉及兩相流問題，Fluent 中解決兩相流問題的典型方法是流體體積（Volume of Fraction，VOF）法，即通過計算單個網格單元內流體體積與網格體積的比值，從而確定自由液面的位置和形狀，該方法簡單易行、收斂精度高且穩定性好。

若某流動問題涉及n相流體，單個網格單元中第i相流體體積分數為qi，則有0≤qi≤1，且流體總的體積分數須滿足式（5）。

對于兩相流而言，若想確定自由液面的位置，只需追蹤qi=0.5 的所有網格單元即可。

1.3 湍流模型

湍流的數值模擬方法中，大渦模擬（Large Eddy Simulation，LES）將大于網格尺寸的湍流渦運動通過控制方程直接得到，再建立近似模型模擬小尺度渦對大尺度渦運動的影響，該方法計算資源消耗大但精度高。Reynolds 平均法（Reynolds-Averaged Navier-Stokes，RANS）對瞬態N-S 方程進行時間平均處理，并且補充反映其特性的湍流輸運方程，其消耗的資源和時間均少于LES，也是目前采用最多的方法。此外還有RANS/LES 混合方法，兼具了RANS 計算量小和LES 精度高的特點。本文采用RANS 中的SSTk-ω模型，其由Menter 提出，考慮了逆壓梯度邊界層的主要剪切應力輸運，可用于逆壓力梯度流動，廣泛用于黏性模擬，適合一般流動和內部流動等問題。

其輸運方程為如下。

式中，Γk和Γω均為代系數；μt為湍流粘度，且有。Gk和Gω來自湍流項，表示為。Yk和Yω是湍流耗散項。

1.4 用戶自定義函數（UDF）

UDF 是用戶利用C 語言編寫的函數，可以被Fluent 動態加載。用戶可以通過UDF 來定義邊界條件，設置材料性質，定義輸運方程中的源項，定義初值等。其作為一個輔助工具在Fluent 數值模擬中應用十分廣泛。本文使用UDF 實現結構的強迫垂蕩運動，調用DEFINE_CG_MOTION 宏，定義結構垂蕩方向的速度，賦予初值，從而模擬結構強迫垂蕩運動。

1.5 垂蕩阻尼和附加質量計算

若給定浮體強迫垂蕩運動的形式為簡諧運動ξ3=Asinωt，則浮體所受水動力可表示如下。

式中，A為垂蕩幅值；ω為運動頻率；F0為受力幅值；φ為相位差。將運動和受力方程整理得到式（9）[4]。

浮體僅發生垂蕩運動，垂蕩方向滿足力平衡方程。

聯并式（9）和式（10），有

式中，c為浮體的阻尼系數；m為附加質量；φ為相位差。

本文通過CFD 計算可得到垂蕩方向的水動力時歷曲線，進而得到受力幅值F0和相位差φ，代入式（11）計算得到垂蕩阻尼系數c和附加質量m。該方法也適用于通過強迫運動形式計算結構的搖蕩阻尼，原理類似。

1.6 無量綱附加質量和無量綱阻尼系數

無量綱附加質量和無量綱阻尼系數是反映結構水動力性能的重要參數。為了探究兩者在不同運動參數下的變化規律，根據文獻[10]中的方法可計算得到上述參數，如式（12）和式（13）所示。

式中，Cd為無量綱阻尼系數；Ca為無量綱附加質量系數；S為投影面積；為結構排水體積。

2 圓筒型FPSO 數值建模及驗證

2.1 FPSO 主尺度參數

圓筒型FPSO 的模型如圖1 所示，主筒體的下部為延伸筒體，圍繞延伸筒體周圍設置有減動結構，能增加結構垂蕩運動時的附加質量和阻尼，從而削減結構運動響應。圓筒型FPSO 的幾何主尺度參數如表1 所示。

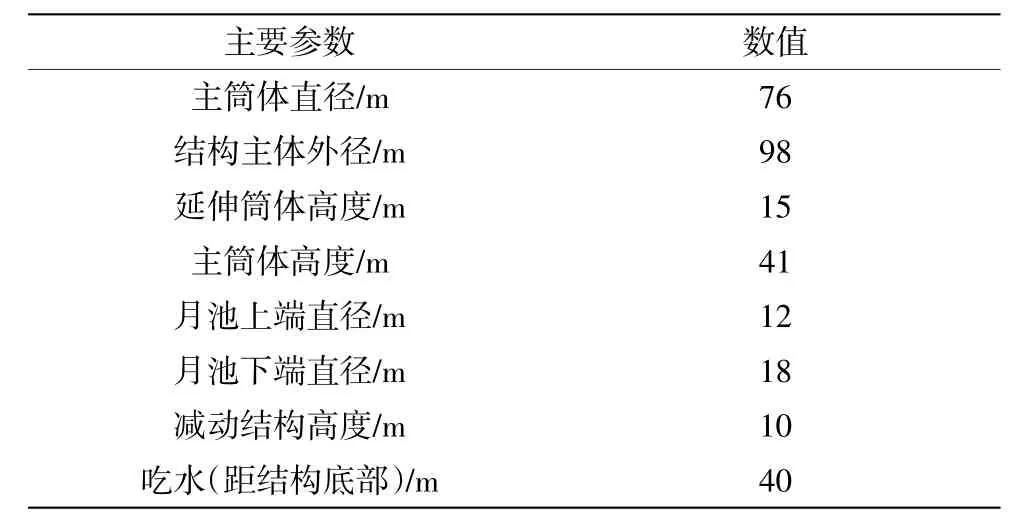
表1 圓筒型FPSO 幾何參數

圖1 圓筒型FPSO 模型

2.2 網格無關性驗證

本文采用Fluent 軟件進行CFD 仿真計算，建立的計算域大小為500 m ×800 m ×380 m，在結構周圍劃分加密網格，且通過UDF 使得結構發生給定周期和幅值的強迫垂蕩運動，實時輸出垂蕩方向的力Fz。邊界條件是左側為壓力入口，右側壓力出口，四周為對稱邊界條件，FPSO 設置為無滑移壁面條件，如圖2 所示。

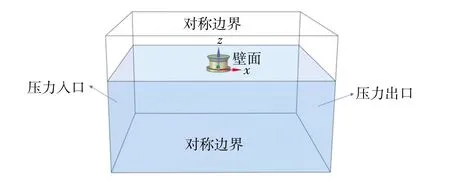
圖2 邊界條件示意圖

為了驗證網格尺寸對于計算結果的影響，通過控制網格疏密程度生成了三種網格方案，選取結構垂蕩運動周期為5 s，幅值為1 m 的工況，對比的計算結果如圖3 所示。

圖3 網格無關性驗證

通過式（12）和式（13）算得無量綱阻尼和附加質量系數結果如表2 所示，隨著網格數量增加，參數結果差異維持在5%以內，可認為網格已趨于收斂，后續計算選用423 萬網格。

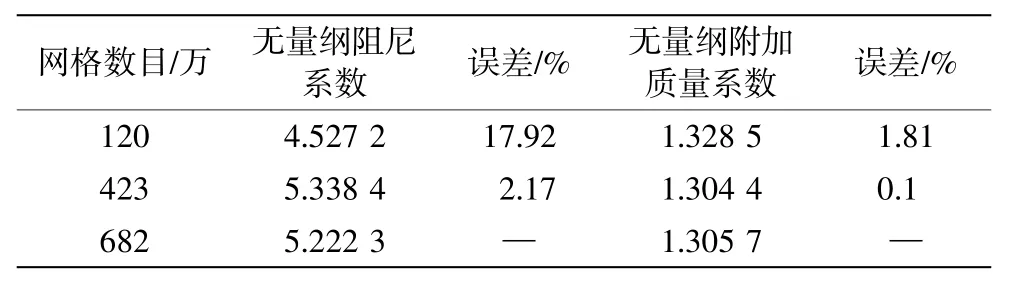
表2 三種網格方案下無量綱阻尼和附加質量對比結果

2.3 時間步長穩定性驗證

為了探究不同時間步長的選取對于無量綱附加質量和阻尼系數的影響，選取時間步長為0.01 s，0.015 s 和0.02 s 三種工況，進行時間步長穩定性驗證。強迫垂蕩運動周期為20 s，幅值為2.4 m，CFD輸出的垂向水動力結果如圖4 所示。

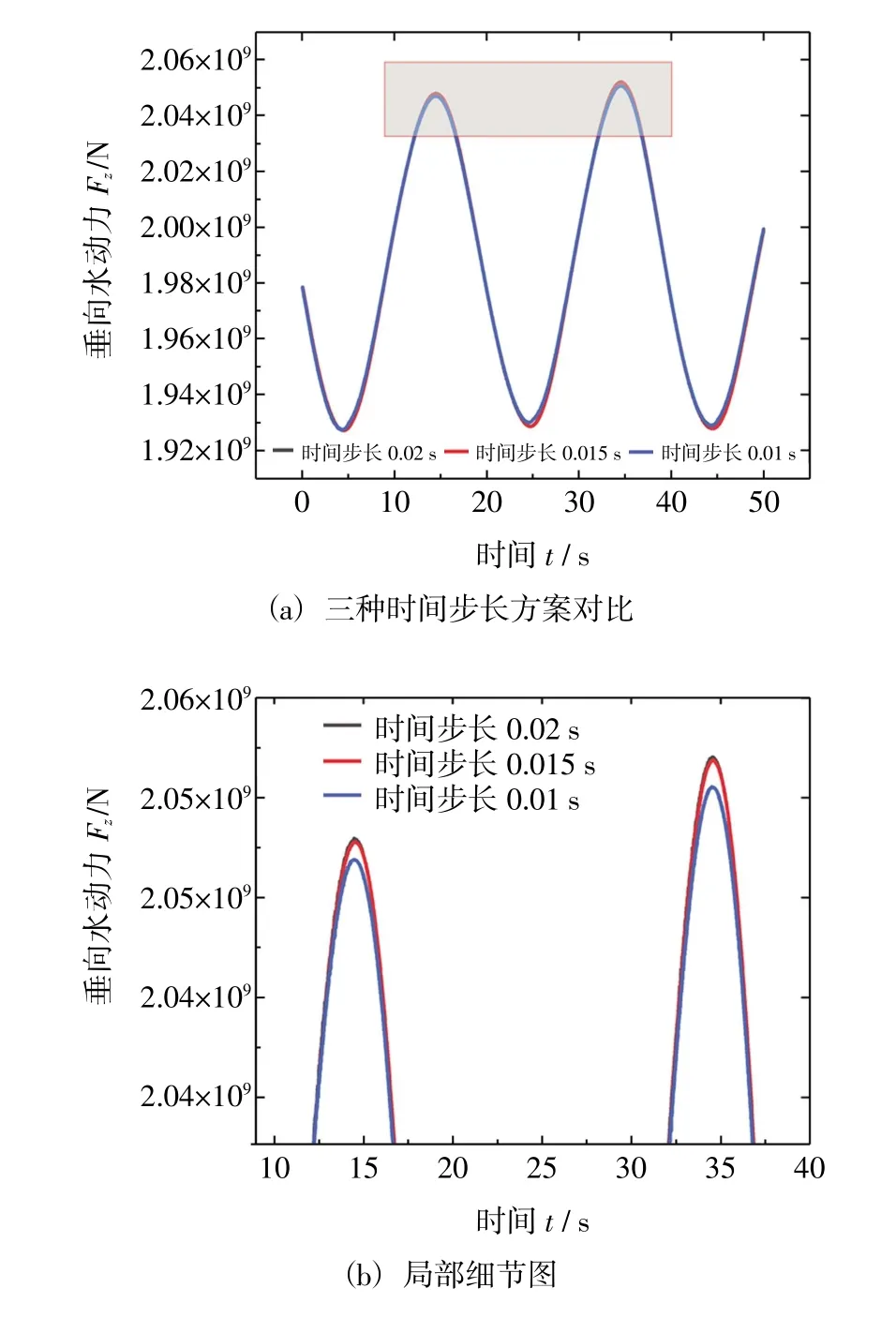
圖4 時間步長穩定性驗證

無量綱阻尼和附加質量系數的結果列舉在表3中。可見，隨著時間步長縮短，計算結果的差異保持在5%以內，且有減小的趨勢，后續計算選用0.02 s 的時間步長。

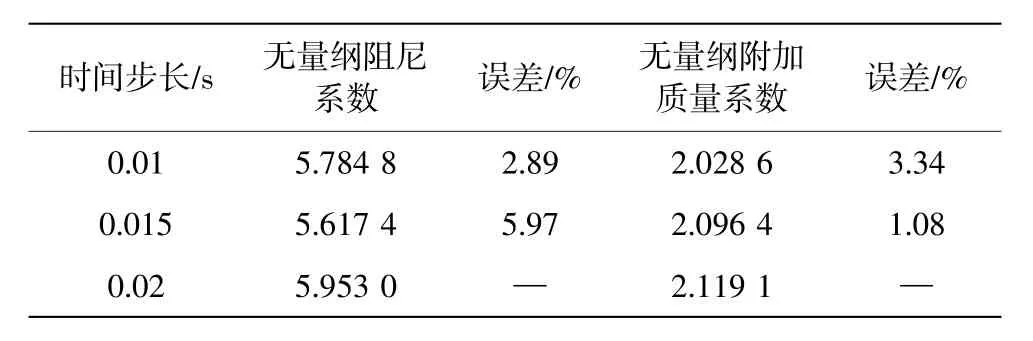
表3 三種時間步長方案下無量綱阻尼和附加質量對比結果

3 計算結果及分析

基于建立的三維數值水池模型，通過軟件Fluent 的用戶自定義函數UDF 模擬圓筒型FPSO 強迫垂蕩運動，運動的周期和幅值通過UDF 編譯設定，輸出垂蕩方向水動力的時歷曲線，擬合后根據式（11）計算得到垂蕩阻尼系數和附加質量。為了探究圓筒型FPSO 在不同的垂蕩周期和幅值下的阻尼系數和附加質量變化規律，本文選取了工程中典型的垂蕩運動周期和幅值范圍，通過Fluent 數值模擬分別計算得到結果如表4 和表5 所示。

表4 不同垂蕩周期和幅值下的垂蕩阻尼系數 單位：N·s·m-1

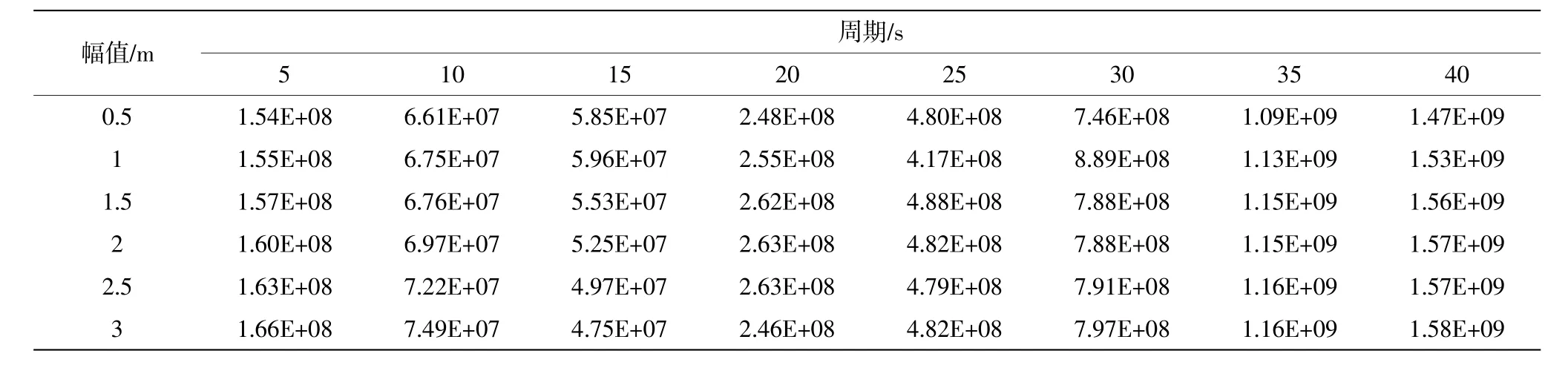
表5 不同垂蕩周期和幅值下的附加質量 單位：kg

圖5 直觀地展示了垂蕩阻尼系數和附加質量與垂蕩運動周期和幅值的關系。可以發現，隨著垂蕩運動周期的增大，垂蕩阻尼系數以較快的速度減小，而垂蕩附加質量在緩速減小后急劇上升。且垂蕩運動周期越大，垂蕩阻尼系數受垂蕩運動幅值的影響越小。當垂蕩運動周期接近垂蕩固有周期時，垂蕩附加質量出現極小值。

圖5 不同周期和幅值下的垂蕩附加質量和阻尼系數

實際海況中，波浪周期接近結構垂蕩固有周期時，會激起較大的垂蕩運動響應。為了探究垂蕩附加質量和阻尼系數隨垂蕩運動幅值的變化關系，取垂蕩運動周期為15 s 時垂蕩附加質量和阻尼系數結果進行對比，如圖6 所示。垂蕩運動周期接近垂蕩固有周期時，垂蕩阻尼系數與垂蕩運動幅值線性正相關，而垂蕩附加質量呈負相關關系。

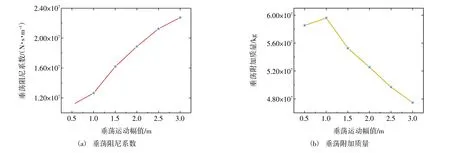
圖6 不同運動幅值下的垂蕩附加質量和阻尼系數（運動周期為15 s）

在表4 和表5 結果的基礎上，為了進一步分析圓筒型FPSO 水動力特征，由式（12）和式（13）計算得到圓筒型FPSO 在不同垂蕩運動周期和幅值下的無量綱阻尼系數和無量綱附加質量系數，結果如表6 和表7 所示。

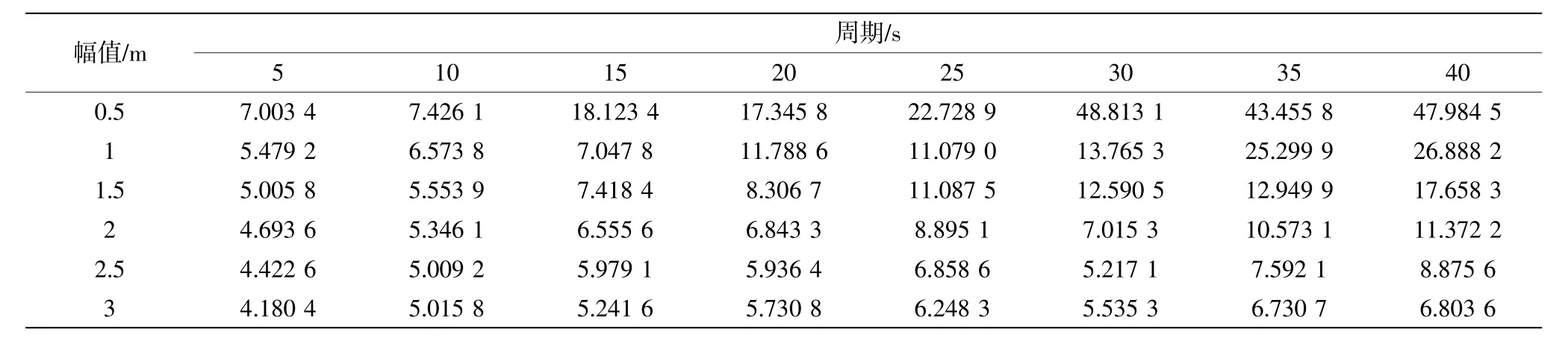
表6 不同垂蕩周期和幅值下的無量綱阻尼

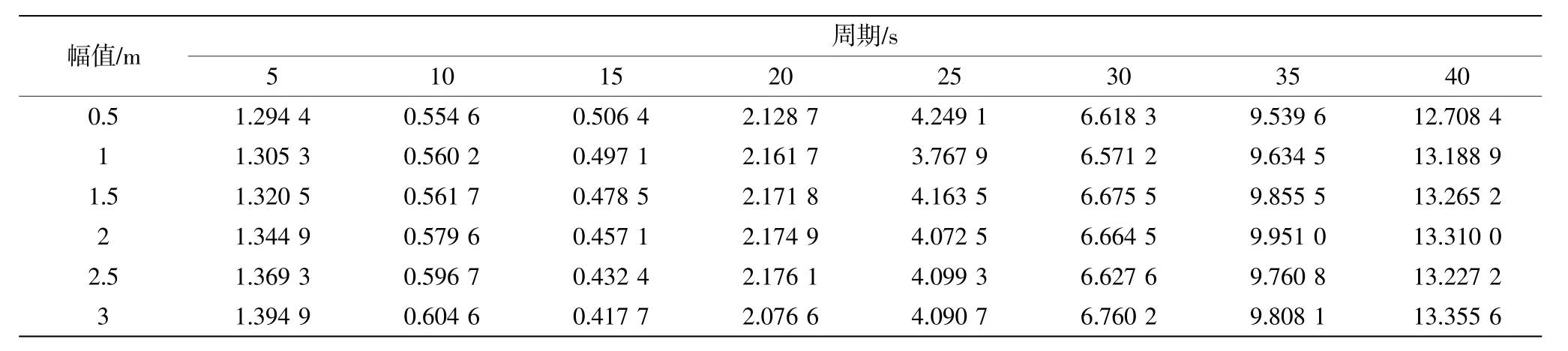
表7 不同垂蕩周期和幅值下的無量綱附加質量

圖7 中展示了無量綱阻尼和附加質量系數隨垂蕩運動周期和幅值的變化規律。結果可知，隨著垂蕩運動周期的增大，無量綱阻尼系數整體呈現出增長的趨勢，這與垂蕩阻尼的趨勢是恰恰相反的。垂蕩運動周期較大時，無量綱阻尼系數對垂蕩運動幅值較敏感。而無量綱附加質量系數的變化規律與圖5（b）中所展示的規律并無大異，且幾乎不受垂蕩幅值的影響。

圖7 不同運動周期和幅值下的無量綱附加質量和阻尼系數

如圖8 所示，當垂蕩運動周期接近結構垂蕩固有周期時，無量綱附加質量和阻尼系數均與垂蕩運動幅值負相關。其中，垂蕩運動幅值較小時（小于1.0 m），無量綱阻尼系數驟降；垂蕩運動幅值達增大到一定值時（大于1.0 m 且小于3.0 m），無量綱阻尼系數緩速減小。

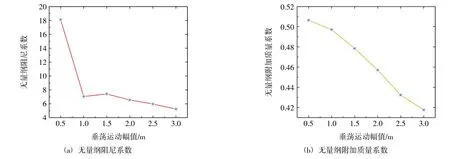
圖8 不同運動幅值下的無量綱附加質量和阻尼系數（周期為15 s）

4 結 論

本文利用CFD 對帶減動結構的圓筒型FPSO 進行了數值模擬，通過模擬結構強迫垂蕩運動，輸出垂向體積力，計算得到不同運動參數下的垂蕩阻尼系數和附加質量，得出以下研究結論。

（1）對于圓筒型FPSO，垂蕩阻尼系數與垂蕩運動周期負相關，與垂蕩運動幅值呈線性正相關，且垂蕩運動周期較小時，垂蕩阻尼系數受垂蕩運動幅值的影響較明顯。

（2）垂蕩附加質量隨著垂蕩運動周期增大呈現明顯上升趨勢，但其對垂蕩運動幅值不敏感。垂蕩運動周期接近垂蕩固有周期時，垂蕩附加質量出現極小值。

（3） 隨著圓筒型FPSO 的垂蕩運動周期增大，無量綱阻尼系數受垂蕩運動幅值的影響愈明顯。具體表現為：無量綱阻尼系數隨著垂蕩運動幅值增大而逐漸減小。

本文研究結果可為圓筒型FPSO 在工程中的應用提供一定參考。然而，本文是采用CFD 的方法計算圓筒型FPSO 的垂蕩阻尼，計算的垂蕩運動周期區間較稀疏，運動幅值范圍并不能涵蓋工程典型海況。此外，垂蕩抑制結構通海能較大程度上改善圓筒型FPSO 的垂蕩性能[11]，利用CFD 的方法探究運動抑制結構通海對于垂蕩性能的改善效果也是一個值得嘗試的思路。