HTPB推進(jìn)劑細(xì)觀損傷及載荷傳遞行為數(shù)值模擬①

逯晗斗,陳 雷,胡松啟,于慶民,3*,白帥帥,劉殊遠(yuǎn)

(1.西北工業(yè)大學(xué) 力學(xué)與土木建筑學(xué)院,西安 710129;2.西北工業(yè)大學(xué) 航天學(xué)院,西安 710072;3.西北工業(yè)大學(xué) 航空學(xué)院,西安 710072)

0 引言

固體推進(jìn)劑作為一種典型的顆粒填充復(fù)合材料,推進(jìn)劑的宏觀力學(xué)性能強(qiáng)烈依賴于細(xì)觀結(jié)構(gòu)。雖然固體推進(jìn)劑類似顆粒增強(qiáng)復(fù)合材料,但不同的是,推進(jìn)劑中的顆粒并不都是起增強(qiáng)作用,顆粒含量增加反而會導(dǎo)致材料更容易受到不可避免的破壞。目前,已有許多國內(nèi)外學(xué)者采用試驗(yàn)和數(shù)值的方法對推進(jìn)劑在細(xì)觀尺度下的損傷進(jìn)行了深入研究。VAN RAMSHORST等[1]基于掃描電子顯微鏡(SEM)研究了固體推進(jìn)劑細(xì)觀形貌與宏觀變形破壞的關(guān)系,發(fā)現(xiàn)載荷作用下顆粒/基體界面脫粘,裂紋沿顆粒/基體界面生長。史佩等[2]基于分子動力學(xué)算法建立了具有高體積分?jǐn)?shù)(60%左右)的固體推進(jìn)劑顆粒填充模型,在此基礎(chǔ)上進(jìn)行的細(xì)觀力學(xué)分析可以有效地考慮固體推進(jìn)劑細(xì)觀結(jié)構(gòu)對其力學(xué)性能的影響。李高春等[3]通過Mori-Tanaka方法將小顆粒和基體等效,然后模擬了大顆粒和等效基體之間的相互作用及“脫濕”損傷,得到的推進(jìn)劑模量和試驗(yàn)結(jié)果吻合。封濤等[4]建立了具有不同細(xì)觀結(jié)構(gòu)的推進(jìn)劑模型,發(fā)現(xiàn)大粒徑AP顆粒界面更容易脫粘,RDX顆粒的界面損傷不明顯,其含量增加會降低初始模量。張建偉等[5]根據(jù)有限元理論及細(xì)觀力學(xué)均勻化方法研究了顆粒體積分?jǐn)?shù)對推進(jìn)劑模量的影響,說明了填充顆粒的增強(qiáng)作用主要體現(xiàn)在瞬時模量上。LI等[6]研究了細(xì)觀結(jié)構(gòu)的力學(xué)性能和推進(jìn)劑中初始界面缺陷對宏觀力學(xué)影響的相關(guān)性。職世君等[7-9]通過在推進(jìn)劑顆粒/基體界面處引入雙線性內(nèi)聚力模型,研究了填充顆粒的含量、粒徑和位置分布等細(xì)觀特征對推進(jìn)劑宏觀力學(xué)性能的影響。另外,張文普等[10]用空氣泡代替了顆粒,根據(jù)模量隨應(yīng)變變化的趨勢,認(rèn)為推進(jìn)劑模量下降的主要影響因素是界面“脫濕”。FRANCQUEVILLE等[11]為了深入了解推進(jìn)劑本構(gòu)與局部損傷、宏觀力學(xué)行為之間存在的關(guān)系,通過單軸拉伸實(shí)驗(yàn),研究了推進(jìn)劑應(yīng)力-應(yīng)變響應(yīng)、體積變化,并根據(jù)受載條件下的掃描電鏡圖像,對局部損傷進(jìn)行了定性描述,同時通過數(shù)值模擬討論了粘聚區(qū)參數(shù)與局部損傷萌生、演化以及粘結(jié)行為與非均質(zhì)材料宏觀力學(xué)響應(yīng)之間的關(guān)系。以上研究主要集中于顆粒“脫濕”這一現(xiàn)象的描述以及討論細(xì)觀結(jié)構(gòu)、界面參數(shù)等變量對推進(jìn)劑宏觀力學(xué)性能的影響,而未考慮顆粒形狀對推進(jìn)劑力學(xué)性能的影響,同時缺少對顆粒和基體之間載荷傳遞能力的定量表征和分析。

為了深入了解固體推進(jìn)劑細(xì)觀損傷的原因以及量化細(xì)觀結(jié)構(gòu)對力學(xué)性能的影響,本文首先通過中心框增長法確定了具有一定細(xì)觀特征的推進(jìn)劑的最佳RVE尺寸,并利用應(yīng)力集中因子及載荷傳遞系數(shù)[12]概念,基于雙線性內(nèi)聚力模型和粘超彈本構(gòu),研究了顆粒形狀、大顆粒含量以及顆粒體積分?jǐn)?shù)對應(yīng)力集中和載荷傳遞系數(shù)的影響,這對揭示復(fù)合固體推進(jìn)劑細(xì)觀結(jié)構(gòu)組成與宏觀力學(xué)行為關(guān)系、量化固體推進(jìn)系統(tǒng)的長期可靠性至關(guān)重要。

1 HTPB推進(jìn)劑各組分材料模型

固體推進(jìn)劑作為一種典型的多相復(fù)合材料,其連續(xù)相基體是一種高分子聚合物,具有較好的力學(xué)性能和較小的粘度,能夠容納大量的固體顆粒;分散相由AP顆粒和Al顆粒組成,為固體推進(jìn)劑提供能量;界面相發(fā)生“脫濕”是導(dǎo)致推進(jìn)劑宏觀斷裂的主要原因。本文基于三相結(jié)構(gòu)(連續(xù)相-界面相-分散相)建立了固體推進(jìn)劑的細(xì)觀損傷模型。

1.1 粘超彈本構(gòu)模型

HTPB固化膠片經(jīng)過單軸拉伸加載和卸載試驗(yàn)后,如圖1所示,完全卸載后,應(yīng)變并未恢復(fù)至0,主要是由于HTPB中的大分子鏈儲存的應(yīng)變勢能,使得卸載階段的斜率明顯小于初始階段,大于軟化階段。根據(jù)其力學(xué)響應(yīng),基體具有超彈性和不可恢復(fù)的粘彈特性。因此,在建立本構(gòu)模型時,需要同時考慮超彈特性和粘彈特性。

圖1 加-卸載名義應(yīng)力-應(yīng)變實(shí)驗(yàn)曲線[13]

選擇Ogden應(yīng)變能函數(shù)描述推進(jìn)劑基體的超彈性力學(xué)響應(yīng):

(1)

式中λi為主伸長率;μi、αi為材料參數(shù);Dk為不可壓縮參數(shù);J為變形后與變形前的體積比,對于不可壓縮材料,J=1。

結(jié)合式(1),可以獲得Ogden超彈性模型關(guān)于應(yīng)力-應(yīng)變的表達(dá)式:

(2)

廣義Maxwell模型可以表征固體推進(jìn)劑靜態(tài)粘彈特性,在ABAQUS中,常用Prony級數(shù)形式來表示:

(3)

式中E∞、Ei和τi分別為平衡模量、第i個Maxwell單元的松弛模量和松弛時間;t為時間。

基于上述粘超彈性理論,Prony級數(shù)和Ogden超彈性模型的相關(guān)系數(shù)如表1和表2所示。

表1 HTPB基體松弛模量主曲線Prony級數(shù)的各階系數(shù)[14]

表2 HTPB基體3階Ogden超彈性模型[15]

1.2 分散相顆粒材料參數(shù)

固體推進(jìn)劑中分散相顆粒模量及強(qiáng)度遠(yuǎn)遠(yuǎn)高于基體,準(zhǔn)靜態(tài)加載過程中,不考慮AP和Al顆粒的損傷,將顆粒視為彈性材料[11]。Al顆粒數(shù)量巨大且粒徑較小,為了降低計(jì)算收斂難度,本文的數(shù)值模擬中僅考慮AP顆粒[16],且假定不同粒徑的AP顆粒材料參數(shù)一致,AP顆粒的彈性模量為19.5 GPa,泊松比為0.25。

1.3 雙線性內(nèi)聚力模型

顆粒和基體的“脫濕”損傷是推進(jìn)劑斷裂失效的主要原因,一般通過內(nèi)聚力模型描述界面的損傷。其中,雙線性內(nèi)聚力模型形式簡單,使用最為廣泛。在實(shí)際情況下,需要采用混合模式準(zhǔn)則來判斷界面的損傷起始點(diǎn)。目前,比較常用的初始損傷準(zhǔn)則是二次應(yīng)力準(zhǔn)則,其表達(dá)式如下:

(4)

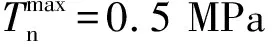
達(dá)到界面損傷起始準(zhǔn)則后,界面開始出現(xiàn)損傷,損傷變量D表示為

(5)

式中D的取值范圍為[0,1],當(dāng)D=0時表示界面未出現(xiàn)損傷,當(dāng)D=1時表示界面完全失效,模擬的裂紋面完全分離。

當(dāng)界面損傷開始演化時,界面剛度會隨之減小,界面剛度與損傷變量的具體關(guān)系如式(6)所示:

(6)

當(dāng)界面等效位移達(dá)到0.02 mm時[17],界面完全失效。為了保證計(jì)算的收斂性,在不影響計(jì)算結(jié)果的基礎(chǔ)上對界面內(nèi)聚力單元引入適當(dāng)?shù)恼承訹18]。

2 HTPB推進(jìn)劑細(xì)觀數(shù)值模型

2.1 RVE尺寸確定

細(xì)觀力學(xué)模型主要利用均勻化技術(shù),從材料的局部本構(gòu)響應(yīng)來確定宏觀材料參數(shù)。均勻化技術(shù)已廣泛應(yīng)用于預(yù)測材料宏觀響應(yīng)的微尺度數(shù)值結(jié)果,均勻化通常是基于代表性體積單元的概念。一方面,RVE尺寸要足夠大,使其可以代表整個宏觀模型的力學(xué)性能;另一方面,RVE尺寸過大會造成計(jì)算資源極大的浪費(fèi),同時也不利于有限元計(jì)算的收斂。因此,在建模時應(yīng)該考慮RVE尺寸的下界,選擇合適的RVE尺寸。

依照經(jīng)驗(yàn)法一般選擇最大顆粒尺寸的3～5倍[19],可選取的RVE尺寸范圍太大,且由于推進(jìn)劑材料的特殊性,無法滿足一些精確計(jì)算。本節(jié)采用數(shù)值方法定量分析了RVE尺寸。為提高計(jì)算可靠性,基于目前推進(jìn)劑配方,建立的模型如圖2所示,其中,模型的RVE尺寸為4000 μm×4000 μm,大顆粒(紅色)粒徑為250～425 μm,體積分?jǐn)?shù)為39.94%,小顆粒(藍(lán)色)粒徑為106～150 μm,顆粒體積分?jǐn)?shù)為22.7%。

圖2 RVE尺寸細(xì)觀模型

采用均勻位移邊界(后續(xù)章節(jié)有對均勻位移邊界條件的具體說明)對上述進(jìn)行單軸拉伸5%。圖3是覆蓋漸增中心方框的單軸拉伸5%細(xì)觀模型應(yīng)變場。如圖所示,采用中心框增長法[20]確定RVE尺寸,該方法使用從應(yīng)變場中心點(diǎn)生長的單個方框,方框尺寸記為R,研究方框內(nèi)平均應(yīng)變隨方框尺寸增長的變化規(guī)律。然后通過評估平均應(yīng)變在一定范圍內(nèi)的收斂性來確定RVE尺寸。為了定量分析RVE尺寸,將方框內(nèi)的局部平均應(yīng)變記作εlocal,整個模型的全局平均應(yīng)變記作εmacro,則方框內(nèi)應(yīng)變變化:

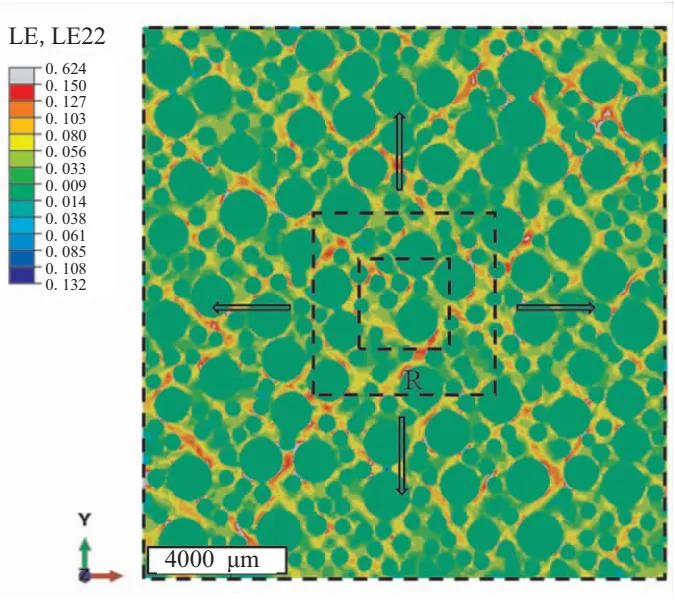
圖3 覆蓋漸增中心方框的細(xì)觀模型應(yīng)變場

(7)

圖4給出了模型應(yīng)變變化參數(shù)隨方框尺寸變化曲線。從圖4中可以看出,隨著方框尺寸的增大,局部平均應(yīng)變接近于施加的全局應(yīng)變,在較低的方框尺寸下,局部平均應(yīng)變與全局應(yīng)變相差較大。依據(jù)5% Strain variation和1% Strain variation將Box size劃分為3個不同的區(qū)域,分別記為Ⅰ、Ⅱ和Ⅲ。在區(qū)域Ⅰ(R<1330 μm)中,隨著方框尺寸的增大,應(yīng)變變化參數(shù)呈振蕩趨勢;在區(qū)域Ⅱ(1330 μm2100 μm)中,應(yīng)變參數(shù)的變化幅度小于1%,而當(dāng)方框尺寸較大時,該參數(shù)依然保持在1%以下,并進(jìn)一步收斂于0,因此獲得了模型的RVE尺寸為2100 μm。

圖4 平均應(yīng)變隨方框尺寸的變化曲線

另外,方框尺寸增加到模型的邊界時,其平均應(yīng)變變化參數(shù)有略微變大的趨勢,主要是施加的邊界條件的干擾。最后,將使用中心框增長法估算的RVE尺寸與經(jīng)驗(yàn)選取RVE尺寸進(jìn)行比對,依據(jù)經(jīng)驗(yàn)一般選擇最大顆粒尺寸的3～5倍[19],RVE尺寸選取范圍過大且因推進(jìn)劑材料的特殊性,無法滿足一些精確計(jì)算。如表3所示,結(jié)果較為接近,說明了采用中心框增長法估算的RVE尺寸可行性。

表3 不同方法確定RVE尺寸

2.2 邊界及載荷

圖5為均勻位移邊界條件以及周期性邊界條件。圖6為不同模型不同邊界條件下拉伸方向應(yīng)力分布,給出了單顆粒模型和多顆粒模型分別在兩種邊界條件下,沿加載方向應(yīng)力分布云圖。對于復(fù)雜的多顆粒模型,不同邊界條件下顆粒發(fā)生“脫濕”損傷的位置幾乎一樣,其拉伸方向的最大應(yīng)力略有差別,均勻位移邊界條件下最大應(yīng)力為20.972 MPa,周期邊界條件下最大應(yīng)力為23.476 MPa;對于單顆粒,應(yīng)力分布完全一致。

(a) Uniform displacement boundary conditions (b)Periodic boundary condition

圖6 不同模型不同邊界條件下拉伸方向應(yīng)力分布

圖7為不同模型不同邊界條件應(yīng)力-應(yīng)變曲線。對于單顆粒模型,不同的邊界條件對應(yīng)的應(yīng)力-應(yīng)變曲線基本吻合;而多顆粒模型中,由于顆粒脫粘的位置具有一定的隨機(jī)性,因此不同的邊界會造成一定的誤差,但仍然小于5%,可以認(rèn)為兩種邊界條件不會造成計(jì)算結(jié)果較大差異。

圖7 不同模型不同邊界條件應(yīng)力-應(yīng)變曲線

對于擁有復(fù)雜細(xì)觀結(jié)構(gòu)的推進(jìn)劑而言,依賴周期性網(wǎng)格實(shí)現(xiàn)周期性邊界條件是十分困難的。因此本文選擇施加較為簡便的均勻位移邊界條件,如圖5(a)所示,僅需對模型下邊界節(jié)點(diǎn)和左邊界節(jié)點(diǎn)的豎直方向自由度和水平方向自由度分別進(jìn)行約束,右邊界通過方程約束使其保持平直,同時對上邊界節(jié)點(diǎn)施加豎直方向位移,上邊界節(jié)點(diǎn)施加均勻位移載荷。

2.3 二維顆粒填充模型建立

HTPB復(fù)合固體推進(jìn)劑的顆粒填充質(zhì)量分?jǐn)?shù)通常高達(dá)60%～80%,同時顆粒粒徑滿足一定的尺寸分布。圖8為HTPB推進(jìn)劑微CT掃描重構(gòu)圖、包含所有顆粒的全配方推進(jìn)劑細(xì)觀模型。

(a) Real mesoscopic structure[22] (b) Filling model with small particles(Volume

從圖8(a)可以看出:AP顆粒的形狀大多接近圓形或橢圓形,在基體中高密度填充,且具有較大的尺寸跨度但大尺寸AP顆粒數(shù)量較少;Al顆粒形狀近似為圓形,其尺寸遠(yuǎn)小于AP顆粒,且填充在AP顆粒之間,均勻分散在基體相之中;部分顆粒的邊緣及內(nèi)部含有微孔洞。

常用的建立固體推進(jìn)劑顆粒填充模型的方法主要有隨機(jī)吸附算法(Random Sequential Algorithm,RSA)和分子動力學(xué)(Molecular dynamics,MD)算法。另外,COLLINS等[23]基于微CT掃描,結(jié)合數(shù)學(xué)統(tǒng)計(jì)重構(gòu)了推進(jìn)劑細(xì)觀結(jié)構(gòu),該方法可以最大程度還原固體推進(jìn)劑真實(shí)形貌,但普適性不好,無法對細(xì)觀結(jié)構(gòu)這一變量進(jìn)行討論。本文通過DIGIMAT軟件,結(jié)合真實(shí)的HTPB推進(jìn)劑細(xì)觀模型,高效、準(zhǔn)確地建立了如圖8(b)所示的推進(jìn)劑細(xì)觀模型,AP顆粒粒徑采用二級配,各組分及尺寸如表4所示,粘合劑及其他助劑等效到HTPB中。將所建模型導(dǎo)入到ABAQUS軟件中,二維細(xì)觀顆粒填充模型視為平面應(yīng)變問題進(jìn)行數(shù)值求解[24],進(jìn)行賦予各組分力學(xué)性能參數(shù)、有限元網(wǎng)格劃分、施加2.2節(jié)中圖5(a)所示的均勻位移邊界條件等前處理工作,之后開始有限元分析計(jì)算。

表4 HTPB推進(jìn)劑基本配方及尺寸[21]

2.4 應(yīng)力-應(yīng)變均勻化

采用直接均勻化的方法,通過Abaqus-Python腳本獲取所有積分點(diǎn)的應(yīng)力和應(yīng)變,以及對應(yīng)的體積或面積權(quán)重,則RVE平均應(yīng)力和平均應(yīng)變的分別定義為:

(8)

(9)

式中 上標(biāo)t表示三角形單元,q表示四邊形單元;V為代表體積元的體積;σij、εij分別為積分點(diǎn)處的應(yīng)力和應(yīng)變;N為單元數(shù)量;Vt、Vq為單元的體積。

根據(jù)顆粒復(fù)合材料的強(qiáng)化機(jī)理,顆粒對基體的直接影響是通過兩者之間的載荷傳遞過程來實(shí)現(xiàn)的。首先,顆粒、基體和復(fù)合材料的平均應(yīng)力分別為σp、σm、σc,進(jìn)而定義顆粒的應(yīng)力集中因子Rp=σp/σc,基體應(yīng)力集中因子Rm=σm/σc,用于表征組分材料的平均應(yīng)力集中程度。類似地,為了定量描述顆粒和基體之間的載荷傳遞行為,可定義載荷傳遞系數(shù)為Rp/m=σp/σm。

3 結(jié)果討論

顆粒位置的分布具有一定的隨機(jī)性,為了研究顆粒位置對計(jì)算結(jié)果的影響,結(jié)合HTPB推進(jìn)劑的配方及填充顆粒尺寸分布規(guī)律,建立了4組具有不同顆粒位置分布的細(xì)觀模型,填充體積分?jǐn)?shù)均為62.7%。

由于模型數(shù)量較多,僅展示了其中3個隨機(jī)模型在不同拉伸階段的剛度下降率(SDEG)云圖分布(SDEG為0表示界面未發(fā)生損傷,SDEG為1表示界面單元完全失效,并刪除失效單元),如圖9所示。可以看出,大顆粒決定了損傷最先發(fā)生的位置,從宏觀角度來看,不同模型大顆粒所占的體積分?jǐn)?shù)是一致的,界面Cohesive單元包含的比例也一致,因此宏觀力學(xué)性能也幾乎一致。但是顆粒位置改變,最先失效的單元位置也隨之改變,如圖9(b)所標(biāo)注的,顆粒位置的隨機(jī)導(dǎo)致界面單元失效的隨機(jī)性,但失效的進(jìn)程并未受到影響,當(dāng)外載應(yīng)變?yōu)?.74%時,不同模型幾乎同時出現(xiàn)界面單元失效。如圖9(c)所示,當(dāng)應(yīng)變達(dá)到20.31%時,大部分大顆粒和極少數(shù)小顆粒都與基體發(fā)生脫粘,由于顆粒之間復(fù)雜的相互作用導(dǎo)致了極少數(shù)小顆粒界面“脫濕”,這進(jìn)一步說明了“脫濕”損傷發(fā)生在大顆粒界面或顆粒聚集的地方,小粒徑顆粒主要起增強(qiáng)作用,基本不發(fā)生“脫濕”損傷。值得注意的是,顆粒位置改變雖然不會影響推進(jìn)劑宏觀力學(xué)性能,但導(dǎo)致空穴出現(xiàn)的位置發(fā)生了改變,從而影響了裂紋擴(kuò)展的路徑。

(a)Strain 5.33%

圖10給出了4組隨機(jī)顆粒位置模型的應(yīng)力-應(yīng)變曲線。可以看出,在彈性階段,應(yīng)力-應(yīng)變曲線完美重合,計(jì)算結(jié)果波動幾乎為0,表明在顆粒級配和體積分?jǐn)?shù)相同的情況下,在“脫濕”損傷前,材料的力學(xué)性能不會受到顆粒位置改變的影響;“脫濕”損傷發(fā)生階段,應(yīng)力出現(xiàn)下降,主要是界面單元逐漸失效,不再承受拉伸載荷,從而導(dǎo)致了應(yīng)力曲線快速下降,由于顆粒位置不同,發(fā)生“脫濕”損傷的位置也不同,計(jì)算的結(jié)果稍有波動,但最大波動也僅5%,可以認(rèn)為總體上不存在明顯的差異;當(dāng)應(yīng)變達(dá)到15%以后,主要是基體承載階段,應(yīng)力-應(yīng)變曲線逐漸匯聚靠攏。

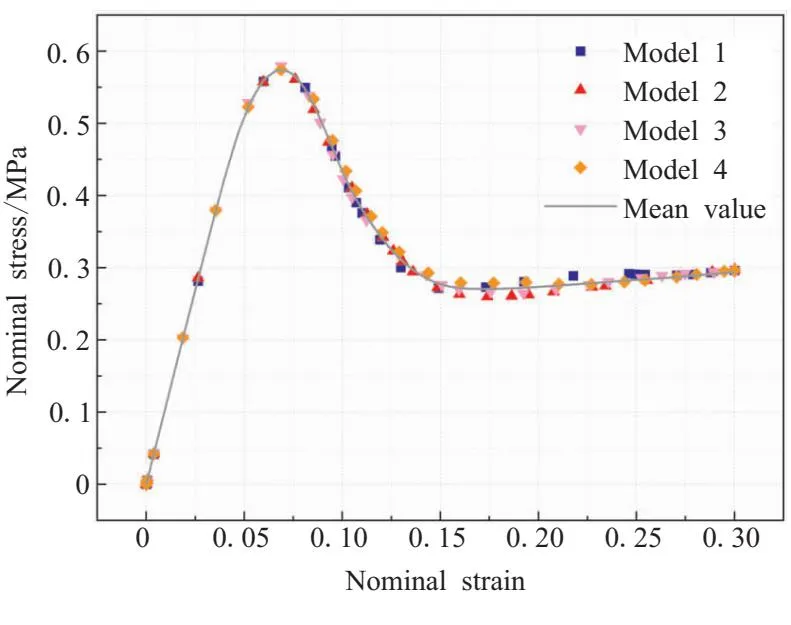
圖10 不同模型應(yīng)力-應(yīng)變曲線

圖11給出了隨機(jī)模型在不同加載階段的面積變化率。在彈性階段,即應(yīng)變?yōu)?.33%時,不同隨機(jī)模型下面積變化率(S-S0)/S0基本一致,其中S0代表RVE模型初始面積(如圖5(a)實(shí)線方框所示),S表示拉伸變形后的面積(如圖5(a)虛線方框所示);當(dāng)拉伸應(yīng)變?yōu)?0.31%時,顆粒位置影響了“脫濕”的位置,導(dǎo)致面積變化率略有差別,如Model 1面積變化率約為18.87%,Model 2的面積變化率約為18.23%,兩者的相對誤差僅為3.5%。

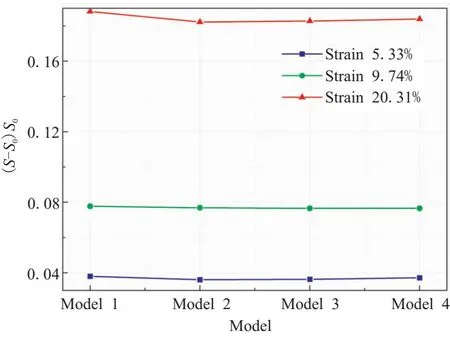
圖11 不同模型的面積變化率

由此可知,當(dāng)顆粒的體積分?jǐn)?shù)和顆粒級配一定時,改變顆粒的位置不會對結(jié)果產(chǎn)生較大影響,因此在后文的計(jì)算中可忽略顆粒位置對結(jié)果的影響。

3.1 顆粒形狀對推進(jìn)劑力學(xué)性能的影響

固體推進(jìn)劑的顆粒并不是理想化的圓形,麥麥提圖爾蓀等[25]對多邊形顆粒填充細(xì)觀模型進(jìn)行數(shù)值計(jì)算,發(fā)現(xiàn)多邊形在突出的頂點(diǎn)附近容易產(chǎn)生應(yīng)力集中現(xiàn)象,容易造成基體撕裂,因此實(shí)際生產(chǎn)過程中一般都會采用較為圓潤的顆粒。本節(jié)僅考慮了橢圓形顆粒,研究了相同體積分?jǐn)?shù)下,顆粒的長徑比(Ap)對固體推進(jìn)劑力學(xué)行為的影響,其中不同形狀的顆粒都是隨機(jī)分布的。

顆粒長徑比越大,顯然越容易發(fā)生應(yīng)力集中現(xiàn)象。圖12(a)給出了應(yīng)變?yōu)?0%時,不同長徑比顆粒的最大主應(yīng)力云圖分布。長徑比增加一倍,顆粒的最大拉伸主應(yīng)力從1.051 MPa增加到1.209 MPa,增幅約為15%;壓縮主應(yīng)力從0.16 MPa增加到0.238 MPa,增幅接近50%。對基體采用同樣的研究方法。圖12(b)給出了應(yīng)變?yōu)?0%時,不同長徑比基體的最大主應(yīng)力分布,當(dāng)長徑比Ap=1.0時,基體的最大主應(yīng)力為16.679 MPa;當(dāng)長徑比Ap=2.0時,最大主應(yīng)力增加到了29.013 MPa,增幅約為74%。

通過載荷傳遞系數(shù),可以有效地表征不同長徑比的顆粒載荷傳遞的效率。圖13給出了不同長徑比下,載荷傳遞系數(shù)的變化趨勢。

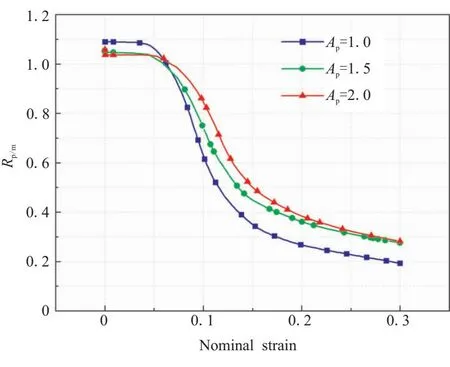
圖13 長徑比對載荷傳遞系數(shù)的影響

由圖13可以看出,在初始階段,載荷傳遞系數(shù)基本保持不變,長徑比越小,載荷傳遞系數(shù)越高,表明越圓潤的顆粒越有利于載荷傳遞;同樣的,載荷傳遞效率越高,界面單元也就越容易發(fā)生損傷。當(dāng)長徑比Ap=1.0時,平均載荷傳遞系數(shù)Rp/m最先開始下降,下降速率也是最快的,主要是初始階段高效率的載荷傳遞導(dǎo)致界面單元失效的數(shù)量最多,界面單元失效后不再承載,從而降低了載荷傳遞效率。長徑比Ap=2.0時,初始階段載荷傳遞效率最低,但同樣卻阻止了界面單元的快速損傷,在應(yīng)變大于10%以后,未失效的界面單元的數(shù)量最多,反而提高了模型的載荷傳遞效率。

3.2 顆粒級配對應(yīng)力集中和載荷傳遞系數(shù)的影響

為了考慮顆粒級配對應(yīng)力集中程度和載荷傳遞效率的影響,分別建立了3個不同的細(xì)觀計(jì)算模型,如圖14所示,模型體積分?jǐn)?shù)都為42.7%。其中,f表示模型的體積分?jǐn)?shù),下標(biāo)AP-1表示大顆粒,粒徑250～425 μm,呈正態(tài)分布;AP-2表示小顆粒,粒徑為150 μm。

(a)Model 1 (b)Model 2 (c)Model 3

加載過程中,不同級配下顆粒和基體應(yīng)力集中因子的變化趨勢如圖15所示。可以看出,對于顆粒來說,其應(yīng)力集中因子Rp在加載的最初階段基本保持不變,而后下降速率開始增大,最后下降速率又開始變緩。基體的應(yīng)力集中因子Rm的變化趨勢與顆粒正好相反,即加載的最初階段基本保持不變,而后上升速率開始增大,最后上升速率又開始變緩。同時,大顆粒含量越高,在初始階段顆粒的應(yīng)力集中程度越大,脫粘后顆粒的應(yīng)力集中程度越小;初始階段基體的應(yīng)力集中程度越小,脫粘后基體的應(yīng)力集中程度越大。以全是大顆粒的模型為例,隨著“脫濕”的進(jìn)行,顆粒的應(yīng)力集中因子先下降,而后趨于平穩(wěn),整體下降的速率逐漸增加而后逐漸減慢,最后顆粒應(yīng)力集中因子趨于0,表明此時基體的應(yīng)力幾乎無法傳遞到顆粒中,整個模型的平均應(yīng)力基本上和基體等效。

圖15 不同級配對應(yīng)力集中因子的影響

圖16給出了不同顆粒級配下,載荷傳遞系數(shù)的變化關(guān)系。在初始階段,載荷傳遞系數(shù)不會隨外加載荷的變化發(fā)生改變,大顆粒體積分?jǐn)?shù)從0增加至42.7%時,載荷傳遞系數(shù)也從0.95增加至1.25,表明初始階段大顆粒含量增加可以提高載荷傳遞效率;隨著應(yīng)變的增加,僅含大顆粒模型的載荷傳遞系數(shù)開始迅速減小,而不含大顆粒模型的載荷傳遞系數(shù)變化不大。載荷傳遞系數(shù)下降主要原因是界面單元損傷發(fā)生失效從而無法傳遞載荷,表明大顆粒含量越多,其界面損傷的進(jìn)程越快,同時界面損傷程度越劇烈,大顆粒更容易脫粘,脫粘以后載荷傳遞比較困難,所以曲線下降更快;隨著拉伸應(yīng)變的進(jìn)一步增加,載荷傳遞系數(shù)進(jìn)入平緩下降階段,當(dāng)應(yīng)變?yōu)?.3時,僅含有大顆粒模型的載荷傳遞系數(shù)接近0,表明大顆粒/基體界面大部分單元均已失效不再承載,大顆粒含量越高,界面“脫濕”損傷也越嚴(yán)重。

圖16 不同級配對載荷傳遞系數(shù)的影響

3.3 顆粒體積分?jǐn)?shù)對應(yīng)力集中和載荷傳遞系數(shù)的影響

針對顆粒體積分?jǐn)?shù)對復(fù)合材料內(nèi)部載荷傳遞行為的影響,以顆粒長徑比為1.0的情況為例進(jìn)行研究。結(jié)合推進(jìn)劑顆粒級配關(guān)系,生成3組不同體積分?jǐn)?shù)的推進(jìn)劑細(xì)觀填充模型,模型對應(yīng)的體積分?jǐn)?shù)分別為22.7%、42.7%和62.7%,如圖17所示。

(a)fAP=22.7% (b)fAP=42.7% (c)fAP=62.7%

不同顆粒含量時,顆粒和基體應(yīng)力集中因子隨外加應(yīng)變的變化規(guī)律如圖18所示。從圖中可以看出,“脫濕”前顆粒和基體的應(yīng)力集中因子差距較小,都在1.0附近;當(dāng)應(yīng)變達(dá)到0.1后,隨著顆粒含量的提高,顆粒和基體的應(yīng)力集中因子都將逐漸增加,這是因?yàn)轭w粒體積分?jǐn)?shù)的變化,會在較大程度上改變復(fù)合材料的平均應(yīng)力。以應(yīng)變?yōu)?0%的階段為例進(jìn)行分析,當(dāng)顆粒體積分?jǐn)?shù)很小時,顆粒的應(yīng)力集中因子也很小,如圖體積分?jǐn)?shù)為22.7%時,顆粒的應(yīng)力集中因子接近0,復(fù)合材料的平均應(yīng)力將會更接近于基體的平均應(yīng)力,同時基體的應(yīng)力集中因子也將更接近于1.0;而當(dāng)顆粒體積分?jǐn)?shù)很大時,復(fù)合材料的平均應(yīng)力將更接近于顆粒,因此顆粒的應(yīng)力集中因子將趨近于0.5,而同時基體的應(yīng)力集中因子接近2.0。

圖18 不同體積分?jǐn)?shù)對應(yīng)力集中因子的影響

體積分?jǐn)?shù)對載荷傳遞系數(shù)的影響如圖19所示。在初始階段,顆粒體積分?jǐn)?shù)越大,載荷傳遞系數(shù)越小,表明初始階段體積分?jǐn)?shù)增加會降低載荷傳遞的效率;當(dāng)拉伸應(yīng)變約0.05時,載荷傳遞系數(shù)開始下降,和改變顆粒級配不同的是,體積分?jǐn)?shù)發(fā)生改變,并不會影響損傷的進(jìn)程,載荷傳遞系數(shù)幾乎同時下降,但會影響其下降的速率。體積分?jǐn)?shù)fAP=22.7%的載荷傳遞系數(shù)下降最快,下降幅度最大,當(dāng)應(yīng)變達(dá)到30%時,載荷傳遞系數(shù)從初始1.2下降至0,表明此時界面損傷嚴(yán)重,應(yīng)力無法通過基體傳遞顆粒;而當(dāng)體積分?jǐn)?shù)fAP=62.7%時,載荷傳遞系數(shù)最大值和最小值的差值明顯小于較低體積分?jǐn)?shù)的情況。在基體承載階段,體積分?jǐn)?shù)越低,其載荷傳遞系數(shù)的變化越平緩,主要是因?yàn)轶w積分?jǐn)?shù)越低,界面相的占比也就越少,當(dāng)大部分單元發(fā)生“脫濕”損傷后,阻止了顆粒和基體之間的載荷傳遞,此時顆粒的平均應(yīng)力接近0,RVE模型的平均應(yīng)力和基體的平均應(yīng)力接近。

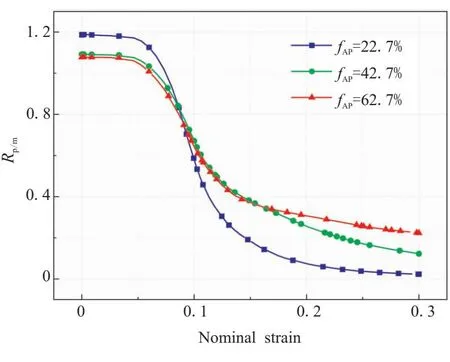
圖19 不同體積分?jǐn)?shù)對載荷傳遞系數(shù)的影響

4 結(jié)論

本文基于粘超彈性本構(gòu)和雙線性內(nèi)聚力模型對HTPB固體推進(jìn)劑進(jìn)行了數(shù)值模擬,研究了推進(jìn)劑細(xì)觀損傷和載荷傳遞特性,得到以下結(jié)論:

(1)相較于經(jīng)驗(yàn)法,采用中心框增長法確定的RVE尺寸更為精確、合理;顆粒位置隨機(jī)并不會對RVE模型的力學(xué)性能造成明顯的影響,這也進(jìn)一步驗(yàn)證了采用RVE模型來代表宏觀推進(jìn)劑的可靠性,但會改變空穴出現(xiàn)的位置,從而影響了裂紋擴(kuò)展的路徑。

(2)顆粒的長徑比越大,初始階段載荷傳遞效率越低,從而阻止了界面單元的快速損傷;相同體積分?jǐn)?shù)下,由于大顆粒的界面處更容易發(fā)生“脫濕”損傷,隨著載荷的增加,推進(jìn)劑的應(yīng)力值及載荷傳遞系數(shù)下降得更快。

(3)體積分?jǐn)?shù)發(fā)生改變,并不會影響損傷的進(jìn)程,但會影響載荷傳遞系數(shù)下降的速率;顆粒填充體積分?jǐn)?shù)主要影響著推進(jìn)劑基體的承載能力,顆粒的體積分?jǐn)?shù)越低,相應(yīng)基體的占比則越大,在“脫濕”后,RVE平均應(yīng)力就越接近基體的平均應(yīng)力。

致謝：本研究得到了173計(jì)劃基金(2021-JCJQ-JJ-0401)、中央高校基本科研業(yè)務(wù)費(fèi)(D5000210602)及西安近代化學(xué)研究所創(chuàng)新合作項(xiàng)目(SYJJ200313)等資助,在此表示感謝!