水下輔助導航的重力異常隨機場分形插值研究

高偉，魯國瑞

( 天津城建大學地質與測繪學院, 天津 300384 )

0 引言

地球物理場和慣性導航系統(inertial navigation system，INS)聯合的輔助導航技術可有效遏制INS誤差累積問題，始終是國內外水下導航領域的研究難點和熱點. 水下輔助導航技術主要包括地磁匹配導航、地形匹配導航和重力匹配導航等. 而水下重力匹配導航通過測量重力信息與地球重力場進行匹配實現導航定位，在重力輔助導航系統運行時，采集重力特征顯著區域的重力信息與重力基準圖對比得到位置信息，實現天空海一體化水下潛器慣性/重力組合導航系統重調[1-4].

地球形狀的不規則性和密度的不均勻性導致地球各點的重力場并不相同，表現為空間位置(經度、緯度、高度)的函數[5]. 因此潛航器可在航行過程中，通過重力測量儀器采集航線途經的重力數據，并與預先存儲的重力數據相匹配，獲得潛航器當前定位信息，進而對INS 累積的位置誤差進行校正[6-7]. 重力輔助導航系統在測量重力場數據過程中，潛航器無需露出或接近水面，測量儀器也無需向外部發射信號或接收外部信號，系統可進行無源、隱蔽的導航定位，潛航器在衛星、無線電定位系統失效或遭受破壞的特殊情況下仍可達到自主隱蔽導航的目的[8-10].

隨著重力測量儀器及空間測量技術的發展[11]，在全球范圍內快速、準確地獲取重力數據成為現實，使得重力輔助導航系統具備校正INS 積累位置誤差的能力[12-13]. 重力輔助導航系統主要有兩種代表性系統，均由Bell Aerospace 研發，分別為于1990 年研制出的重力梯度導航系統[14]，以及于1991 年研制出的重力輔助INS[15]. 重力輔助導航系統由INS、重力測量儀器、數字重力基準圖[16]和匹配定位算法等四個主要部分組成，各組成部分的性能差異對重力輔助定位系統的性能有重要影響. 數字重力基準圖(重力模型)是重力輔助定位的基礎[17-18]，重力基準圖描述是否準確，包含的重力特征是否豐富，分辨率是否滿足需求，都會影響重力輔助導航系統的性能[19].

為減小線性化誤差，對重力異常參考地圖進行預處理，選擇合適的計算模型對地圖進行插值逼近，得到高分辨率、小格網地圖，以減小線性化誤差對位置觀測精度的影響. 在重力異常數據匱乏的地區，隨著相鄰點間的插值數的增加，擬合函數和Kriging 方法無法滿足逼近精度要求. 其中，擬合函數法跟插值的規模、控制點數目、控制點統計特征和地圖統計特征差異、地圖統計特征相關，不適宜重力異常數據匱乏的區域，而Kriging 方法不適合大尺度條件下的重力插值，因此采用分形重構模擬真實的重力環境，為系統提供良好的仿真環境. 分形通常被用在模擬真實地表和其他自然形態的描述中，它用分維數表達數據場的統計特征. 與Kriging 方法的空間變異函數相似，低分辨率地圖不利于長距離的統計特征描述[20-22]. 本文考慮在這種條件下，提出利用分形插值的方法對重力異常隨機數據場進行重構，重構模擬將為水下重力輔助INS 提供更接近真實的重力環境[23].

分形就是對不規則和支離破碎的自然形狀的描述，分形理論的發展促進了利用它對各種自然形態描述的研究. Goodchild 在1980 年考慮用分形理論分析地文表面，后來Clark 和Schweitzer 定義了具有更好魯棒性的對地形表面分形估計. 從1991 年開始，Kenichi Arakawa 和Eric Krotkov 對“利用分形重構自然地形”進行了研究，利用分形布朗運動(fractal Brownian motion, FBM)在不規則采樣點集上估計自然地形的分形結構，并以此為基礎構造出自然地形，Naokazu 等給出基于FBM 模型的插值方法并不斷進行完善[24].

本文提出采用FBM 分形插值方法對重力異常隨機場進行重構，構造可用于水下重力輔助導航系統的重力異常基準圖，通過實驗驗證分形插值方法的可行性，將為水下重力輔助導航系統的實現提供理論參考.

1 FBM 函數及分維數估計

布朗運動(Brownian Motion，BM)是1982 年英國植物學家R. Brown 發現的，1923 年德國數學家N.Wiener 建立了BM 的數學模型. BM 是一種隨機過程B(t)，滿足以下兩個條件：

式中：C為常數；隨機過程的任意兩點之間(B(b)-B(a)和B(c)-B(b),a≤b≤c) 的增量是相互獨立的.

B(t)被寫成

顯然，它具有自緊密性.

Mandelbrot 提出FBM 函數，由它產生BM 過程.

Penland 定義了FBM 函數統計自相似性特征

式中：f(t) 為FBM 函數；g(x) 為累計分布函數(g(x)～N(0,σ2))；H為自仿射參數，它與f(t) 的分維數D之間的關系為

n是幾何拓樸維數，在重力異常地圖中，n=2 .

由式(6)可得

又

可以得到

兩邊取對數

在對二維隨機數據場進行分維數估計時， Δt用地圖上兩點距離代替，則

2 重力異常地圖分維數估計

重力異常地圖的分維數的估計也是以式(11)為基礎進行的.

在計算時需要得到在不同 ΔX下的E[|f(X+ΔX)-f(X)|]，顯然在重力異常地圖陣列的基礎上，可以得到的 ΔX是離散的，它的取值與地圖網格單位距離和地圖陣列的規模有關，如圖1 所示.

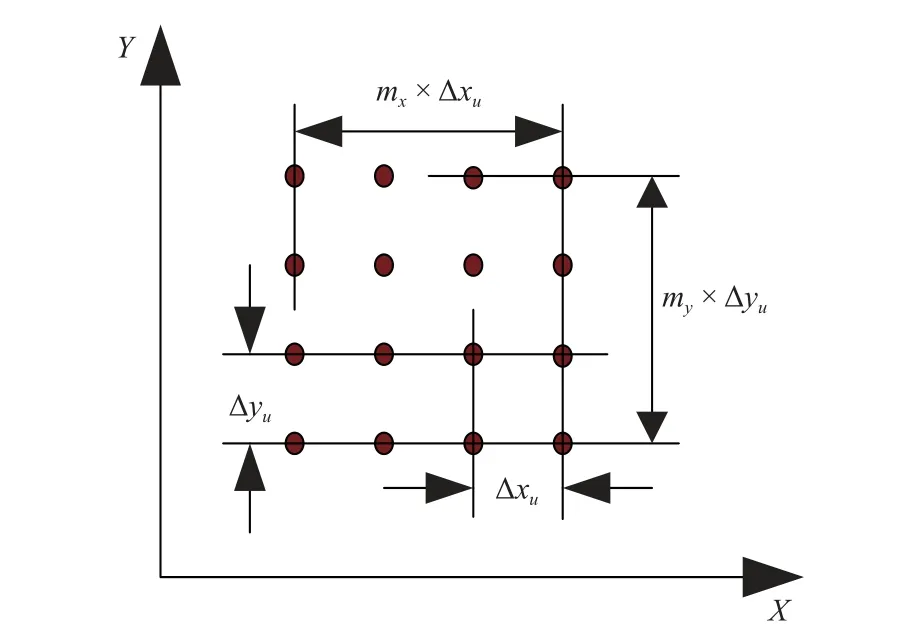
圖1 地圖網格示意圖

能取的距離為ΔX

式中，i=1,2,···,mx；j=1,2,···,my；這里僅討論ux=uy=u的情形.

顯然，ΔX增加，在計算時，可參與統計點數目會急劇減少. 基于該思路，設定距離容差，可以更好地反映地圖的統計特征.

即，設 εx為距離容差，當地圖上兩點距離滿足

那么，兩點重力異常增量可以計入與ΔX對應的計算中.其中，ΔXP是兩點之間的實際網格距離.

按此方法分別對2 個地塊區域的重力異常地圖進行了分維數計算，結果如圖2 所示.

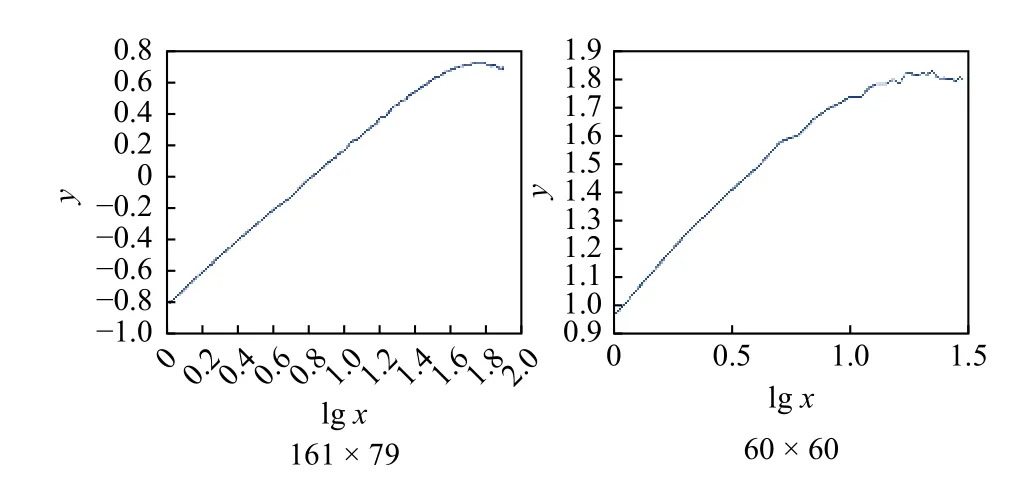
圖2 重力異常地圖分形特征曲線

用最小二乘法擬合直線，得到的結果如表1 所示.

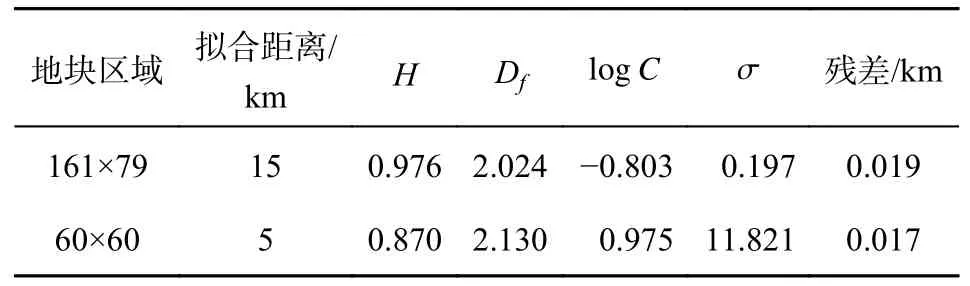
表1 分形特征計算結果

3 FBM 分形插值方法

用FBM 分形插值，生成新的小尺度重力異常地圖的基本步驟如圖3 所示.

圖3 分形插值方法基本流程

分形特征一個有限的尺度范圍內才能充分體現，這個范圍稱為無標度區間 [ΔXmin,ΔXmax] .

由地圖得到的分形特征無標度區間的下限由地圖間隔決定

其上限為分形特征曲線線性擬合區域的上限.

分形插值后得到地圖的最小尺度uc小于u，因此分形插值所能得到的最小尺度不能由原始地圖確定.本文所討論的重力異常地圖分形插值只能用于重力異常地圖的粗插值.

分形插值采用隨機中點位移法，即插入點附近區域的點理解為一個符合 (0,σ2) 的隨機數據與區域的平均值的和，它的實現如圖4 所示.

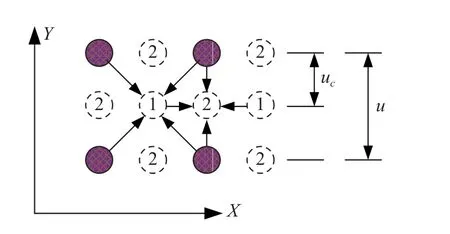
圖4 中點位移插值法

在圖4 中，填充點為原始地圖的控制點，虛線是插值點；插值點分為兩類，標號為1 的插值點 (x,y) ，由其周圍的4 個原地圖控制點為參照進行插值

標號為2 的插值點，所用到的參照點由兩個原地圖控制點和標號為1 的兩個插值點構成

其中， Gauss 是符合均值為0，標準差為1 的隨機信號.

4 實驗結果與分析

4.1 與原始地圖比較

針對某塊 60×60 的重力異常地圖進行插值，在原始地圖上進行等間隔抽樣得到一塊 30×30 的地圖，然后用上述分形插值方法進行插值，并對插值地圖和原始地圖進行比較. 抽樣后的地圖分形特征如表2所示.

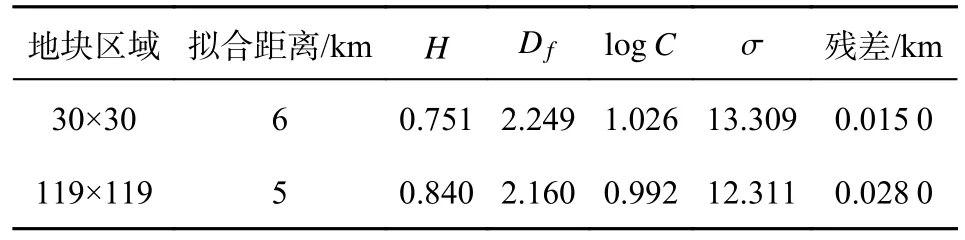
表2 分形特征參數表

插值后的重力異常地圖與原始地圖的比較如圖5所示.

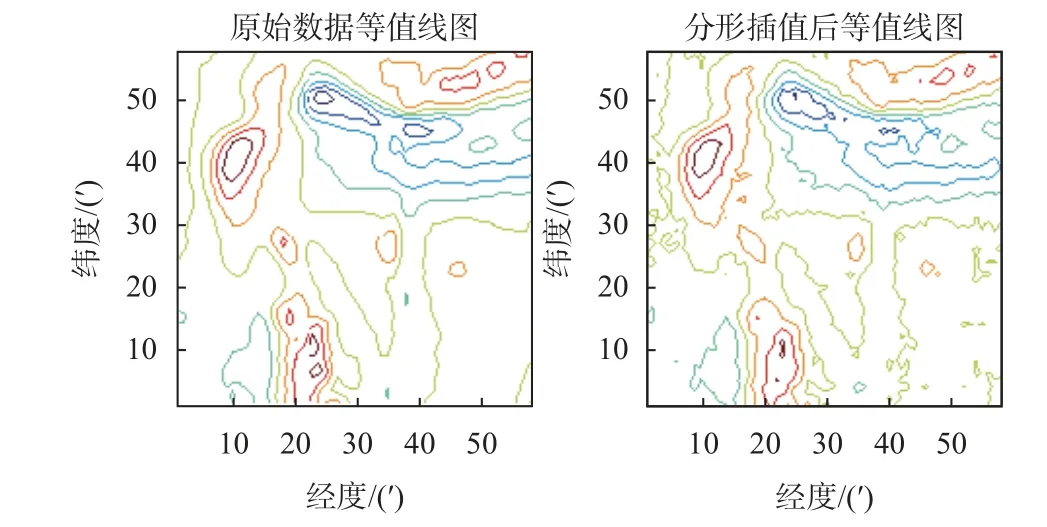
圖5 在原始數據上抽樣后分形插值結果

插值后的精度分析如表3 所示，采用誤差平均值(E(ge))、絕對誤差平均值、絕對誤差最大值(max(|ge|))、誤差均方值和絕對誤差標準差(D(ge) )等參數來評定.

表3 分形插值精度分析

4.2 與原重力異常地圖比較

在原重力異常地圖上進行插值，分析插值后地圖的分形特征的變化. 圖6 是插值后的等值線圖比較.圖7 是插值后地圖分形特征曲線. 其特征參數見表2第2 行數據.

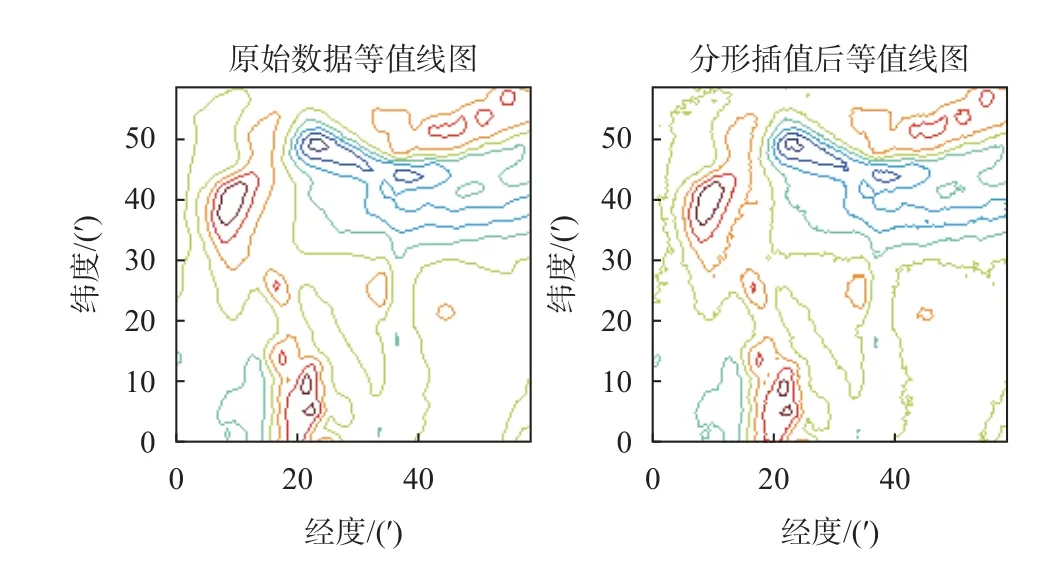
圖6 原始數據直接分形插值結果

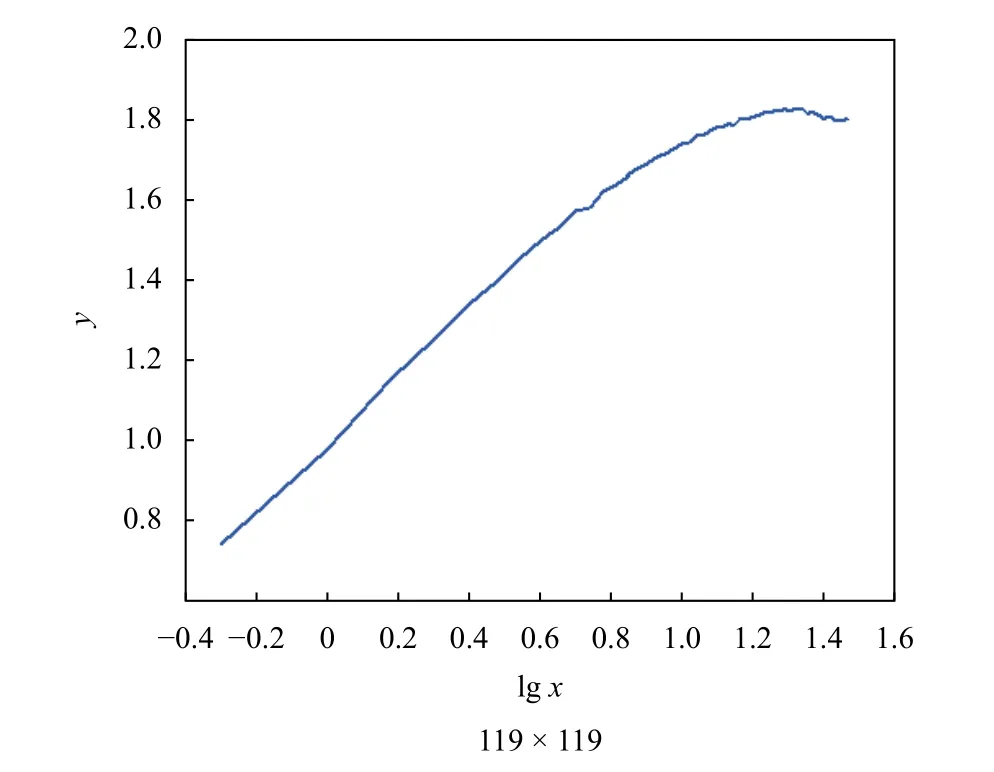
圖7 插值后地圖分形特征曲線

顯然，插值后的地圖與插值前地圖的分形特征變化很小. 分形插值的精度與標準差相關，標準差越大，精度越低；分形插值引入隨機信號，因此插值點的重力異常值具有不確定性；采用中點位移法的插值，插值點位置固定，即uc=u/2 .

分形插值作為地形自然表面的重構方法，具有很強的真實感. 重力異常與地形之間的關聯性，產生了利用分形對重力異常進行插值的聯想，為得到可靠的重力異常地圖的分維數，在分維數定義中加入距離容差，改善了分維數在長空間距離下的統計特征描述.分形插值的精度雖然低，但插值后的地圖仍保持原重力異常參考地圖的統計特征，該方法為仿真提供了很好的環境模擬. 由于條件的限制，雖然沒有對插值結果進行實際測量的驗證，但從計算機仿真實驗結果看，分形插值作為一種粗插值是可行的.

本文是針對水下重力數據匱乏區域的重力場仿真研究，由于數據異常和條件差，分形插值的實驗結果僅與原始數據的計算結果進行了對比研究. 由于重力數據的匱乏，采用其他插值方法的效果不太理想，限于篇幅和數據條件，未進行詳細分析，但后續仍需要通過獲取大量實測數據來進行反復驗證與探討.

5 結束語

本文針對重力異常數據匱乏的地區，提出了采用FBM 分形插值方法對重力異常隨機場進行重構，實現可用于水下重力輔助導航的重力異常基準圖生成. 實驗結果表明，分形插值后的地圖與插值前地圖的分形特征變化很小. 分形插值的精度與標準差相關，標準差越大，精度越低；分形插值引入隨機信號，因此插值點的重力異常值具有不確定性；采用中點位移法的插值，插值點位置可固定. 分形插值作為地形自然表面的重構方法，具有很強的真實感. 從數值模擬結果來看，分形插值方法作為一種粗插值是可行的和有效的，可為水下重力輔助INS 提供更接近真實的重力環境，為水下重力輔助導航系統的實現提供理參考.