基于數據分解的空中交通流量預測模型

摘要 隨著全球經濟一體化步伐加快，航空領域迎來空前發展機遇，國內民航事業蓬勃發展，國內各大航空公司航班飛行量急劇增加，有限的空域資源與不斷增長的空中交通流量之間的矛盾日益突出，而空中交通流量是空中交通管理的基礎環節。因此，文章進行了實例驗證分析，將某管制區域2011—2017年季度空中交通流量數據作為歷史觀測數據，預測2018年四個季度的空中交通流量，通過算例分析，該模型的預測精度為0.383 1（MSE）、0.485 6（MAE）、1.163 7%（MAPE），預測精度滿足要求且高于直接使用灰色預測模型進行預測時的精度。

關鍵詞 數據分解；灰色預測；季節指數

中圖分類號 V355 文獻標識碼 A 文章編號 2096-8949（2023）23-0001-04

0 引言

隨著民航業務量的逐漸恢復，空中交通流量增長顯著，空域資源日益緊張，有限的空域資源與不斷增長的空中交通流量之間的矛盾日益突出。空中交通流量管理可以為空域交通安全、升降有序和流量的加速提供服務，保證空域交通在同一時間內，能夠以最優的方式分布在指定空域內，為各大航空公司提供及時、高效、精準的航空線路部署，更加準確地反饋飛行實時信息，從而減少并避免延誤情況發生。而解決這些問題的前提就在于對中長期空中交通流量進行合理、準確地預測，科學、準確的空中交通流量預測結果可為空中交通管理部門提供空域規劃、交通管制等決策的依據，能有效地緩解空中交通流量增長帶來的管制壓力，通過研究分析得出真實有效的預測模型。

1 預測模型

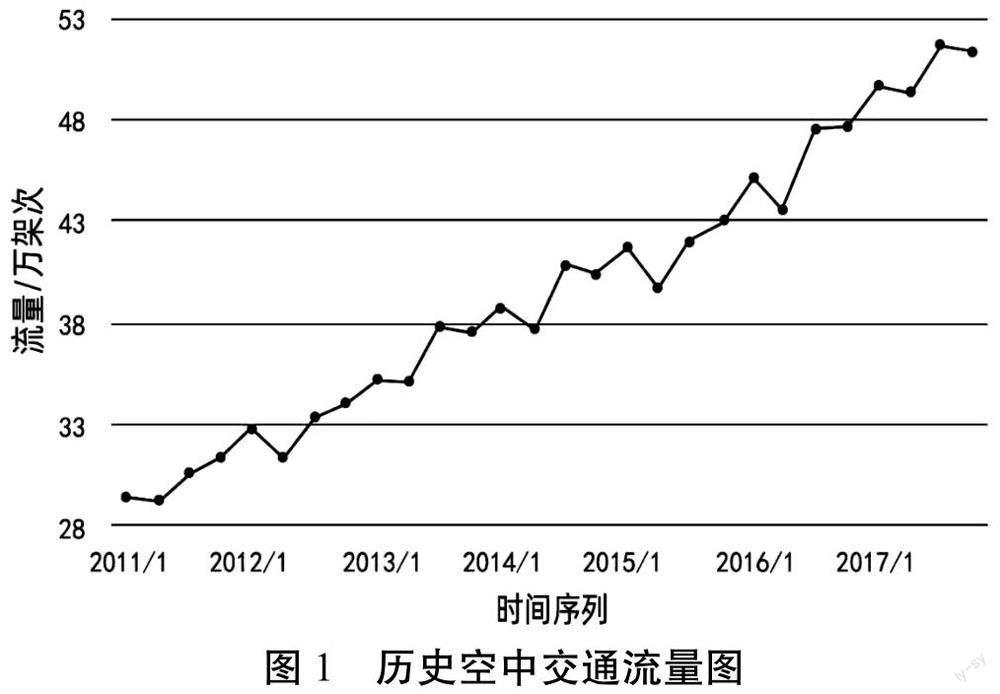
最早的預測模型是傳統的統計模型，一般是通過分析時間序列的趨勢情況以及周期性，經過長期統計，整理出其大概規律，從而進行有效預測。依托傳統的統計模型，在其基礎上開展定向研究，通過對歷史空中交通流量數據的觀測與分析，經過認真對比，發現隨著時間不斷發展的季空中交通流量，雖然呈整體上升趨勢，但在上升的同時又存在一些隨季節變化的季節性波動，成圖分析后，發現波動幅度具有一定規律，如圖1所示^[1]。

根據時間序列發展與歷史空中交通流量觀測數據波動預測假設：

L（t）=Q（t）×J（t） （1）

式中，L（t）——季空中交通流量；Q（t）——趨勢因數；J（t）——季節性波動^[2]。

因此得出假設季空中交通流量L（t）由趨勢部分Q（t）與季節性波動J（t）組成。

1.1 分離趨勢部分

隨著科學技術的不斷發展，數字信號的高精度處理在各行業的高端領域得到了廣泛的需求，信號噪聲對數據準確性帶來了極大影響，降噪技術也就由此得到快速發展。小波變換是一種建立在小波變換多分辨分析基礎上的算法，它繼承和發展了短時傅立葉變換局部化的思想，同時又克服了窗口大小不隨頻率變化等缺點，能夠提供一個隨頻率改變的“時間—頻率”窗口，是進行信號時頻分析和處理的理想工具。最主要的優點是，可以處理多種類型的信號，做到精準降噪、去噪，包括高斯噪聲、脈沖噪聲、周期性噪聲等，同時小波變換法降噪技術還能夠有效保留一些信號的重要信息，具有較高保真性^[3]。其基本思想是根據噪聲與信號在不同頻帶上的小波分解系數具有不同強度分布的特點，將各頻帶上的噪聲對應的小波系數去除，保留原始信號的小波分解系數，得到純凈信號，其原理如圖2所示。

通過小波變換的降噪處理，過濾出的低頻信號即為趨勢部分Q（t），高頻為由于季節性波動而出現的流量。根據上訴預測的假設模型，分析出精準數據，初步得出預想，從而進行更深一步的推論^[4]。

1.2 計算季節指數

根據趨勢部分與歷史觀測數據計算季節比率K：

k_{i， j}=l_{i， j}（t）/q_{i， j}（t） （2）

式中，i——年份；j——季度；k_{i， j}——第i年第j季度的季節比率；q_{i， j}（t）——第i年第j季度的趨勢部分流量；l_{i， j}（t）——第i年第j季度的歷史觀測流量。

計算季節指數P：

P=（p₁， p₂，p₃， p₄） （5）

式中，n——歷史觀測數據年數；h——季節比例系數；p₁——第一季度的季節指數；p₂——第二季度的季節指數；p₃——第三季度的季節指數；p₄——第四季度的季節指數。

1.3 趨勢部分預測

灰色預測是一種對含有不確定因素的系統進行預測的方法。灰色預測通過鑒別系統因素之間發展趨勢的相異程度，即進行關聯分析，并對原始數據進行生成處理來尋找系統變動的規律，生成有較強規律性的數據序列，然后建立相應的微分方程模型，從而預測事物未來發展趨勢的狀況^[5]。由于季度空中交通流量經過小波變換的降噪處理后仍會存在一些不確定因素造成的隨機流量，因此選用灰色預測模型對趨勢部分進行預測，確保其準確性。

灰色預測模型如下所示：

設

Q（t）=X^（0）=[x^（0）（1）， x^（0）（2），…， x^（0）（n）]， x^（0）（g）≥0，

i=1，2，…，n （6）

則X^（0）的一次累加生成序列為

X^（1）=[x^（1）（1）， x^（1）（2），…， x^（1）（n）] （7）

1.5 精度判定

由于預測模型在灰色預測模型的基礎上進行了數據處理，因此不能直接使用灰色預測模型的精度判定方法判斷模型精度。為了評價模型的預測精度，該文選取了空中交通流量預測研究中常用的三個指標來作為評判標準，即平均絕對偏差（MAD）、均方誤差（MSE）和平均絕對誤差百分比（MAPE），其計算公式如下所示：

式中，x_i——i時刻實際的空中交通流量；e_i——i時刻空中交通流量觀測值與預測值之間的誤差。

2 預測流程

根據預測內容及預測相關的需求，結合數據分析、流程設計等因素，將所建模型及求解方法進行邏輯式梳理，按照具體步驟，采用相關計算機軟件進行編程，對上述步驟進行算法實現并進行數據反推，驗證流程閉環，經校驗后，確定具體步驟如下：

（1）使用小波變換法，將歷史空中交通流量數據分解為趨勢與季節性波動兩部分。

（2）針對季節性波動，結合趨勢流量與歷史觀測流量計算季節指數。

（3）使用灰色預測模型，對趨勢部分進行預測。

（4）在趨勢部分預測結果的基礎上還原季節性波動。

（5）對預測結果進行綜合比對，并分析該文方法的預測精度。

預測流程如圖3所示。

3 算例分析

為確保模型準確性，通過與某航空公司進行數據共享，經過前期數據采集整理，選擇較為有代表性的區間段，某管制空域2011—2017年的季度空中交通流量數據作為歷史交通流量數據，使用基于數據分解的空中交通流量預測模型對數據進行預測，并與使用灰色預測模型得到的預測結果進行對比分析，得到具體數據結論。

3.1 計算季節指數

首先使用小波變換對歷史交通流量數據進行降噪處理，降噪效果如圖4所示。

由圖4可知，降噪后的數據平滑且呈上升趨勢，較好地分離了季節性波動，因此可作為趨勢部分進行灰色預測，并計算季節指數，季節指數如表1所示。

3.2 數據預測與精度判定

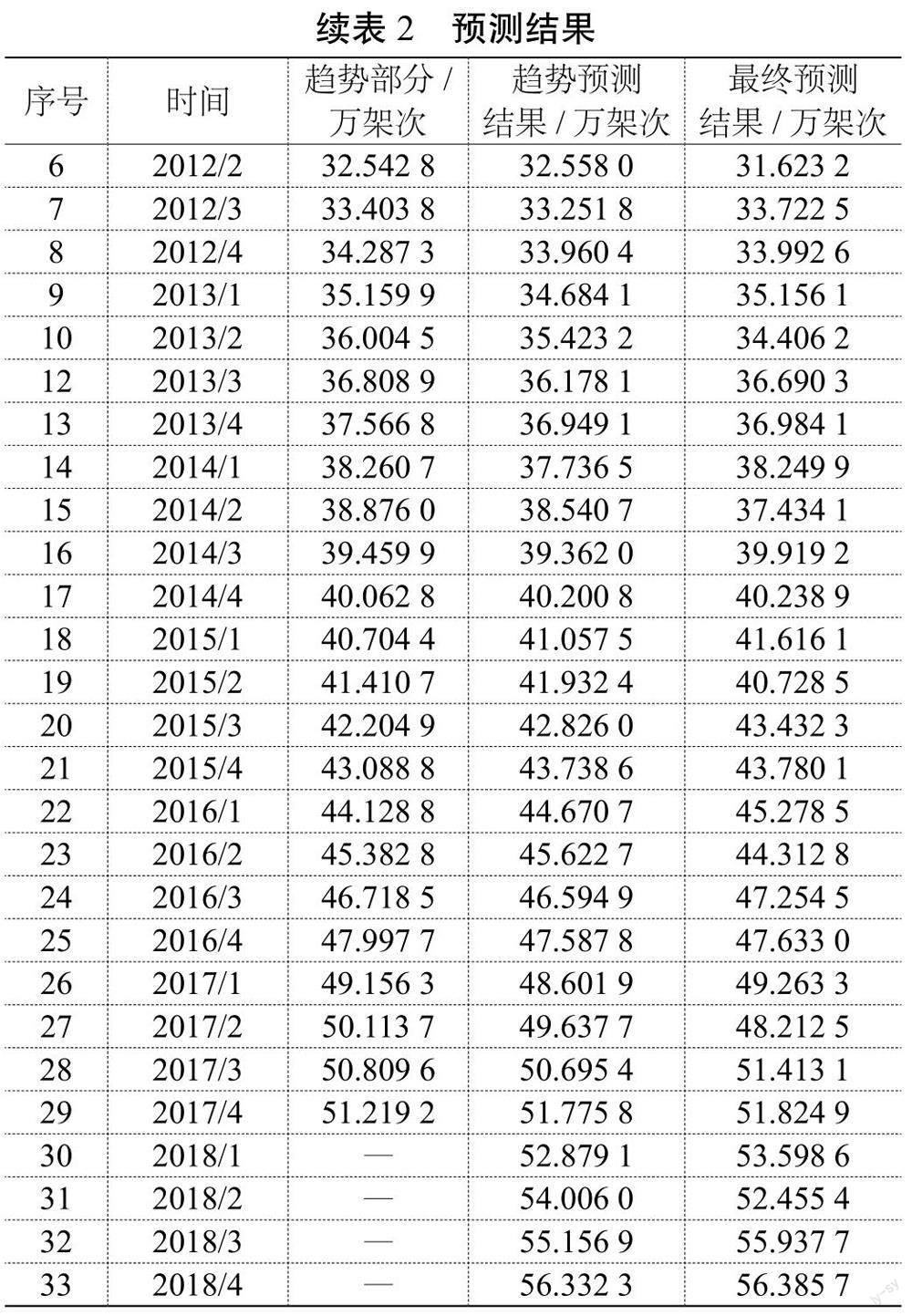
使用灰色預測模型對趨勢部分進行預測，得到預測結果后依據季節指數還原季節性波動得到最終預測結果，對趨勢部分的預測結果及最終預測結果如表2所示。

預測精度及預測效果如表3、圖5所示。

由圖5、表3可知，相對于灰色預測模型，基于數據分解的空中交通流量預測模型較好地模擬了空中交通流量隨時間發展的季節性波動，且使用基于數據分解的空中交通流量預測模型得到預測結果的MAPE、MAE、MSE均低于使用灰色預測模型得到預測結果的MAPE、MAE、MSE，因此說明基于數據分解的空中交通流量預測模型建立成功，且具有較好的預測精度。

4 結束語

基于數據分解的空中交通流量預測模型將空中交通流量數據分解為趨勢部分與季節性波動，通過對趨勢部分預測并還原季節性波動得到最終預測結果，具有較好的預測精度。該預測方法解決了常用預測方法對于存在季節性波動非平穩時間序列預測準確性不高的問題，對空中交通流量管控提供更加精確的數據信息，適用于存在季節性波動的空中交通流量預測問題。

參考文獻

[1]趙玉環， 石新華. 基于時間序列的空中交通流量灰預測模型算法[J]. 中國民航大學學報， 2007（6）： 54-57.

[2]趙玉環， 郭爽. 考慮隨機因素的空中交通流量預測模型研究[J]. 中國民航大學學報， 2008（4）： 59-61.

[3]張明， 韓松臣， 黃林源. 基于雙重力模型和人工神經網絡的空中交通流量組合預測[J]. 西南交通大學學報， 2009（5）： 764-770.

[4]陳丹， 胡明華， 張洪海， 等. 考慮周期性波動因素的中長期空中交通流量預測[J]. 西南交通大學學報， 2015（3）： 562-568.

[5]陳艷彥， 陳子辰， 張兆寧. 基于Logistic模型的空中交通流量中長期預測研究[J]. 科技創新與應用， 2020（27）： 27-29.

收稿日期：2023-10-16

作者簡介：朱曉波（1973—），女，本科，高級工程師，研究方向：通信工程。