船式拖拉機直線工作參數優選研究

張 超,黑曉濤,瞿兆杰,張道德,2

(1.湖北工業大學 農機工程研究設計院,武漢 430068;2.湖北省農機裝備智能化工程技術研究中心,武漢 430068)

0 引言

在南方水田中,履帶式拖拉機、輪式拖拉機等傳統動力機械工作時會導致水田泥腳加深,耕作層破壞,形成較多暗溝,從而造成后續田間作業難以進行[1]。船式拖拉機將“浮”和“滑”原理結合起來,有效地克服了上述問題,在深泥腳水田作業中得到廣泛應用[2-5];但是,因葉輪行駛阻力較大、滑轉率較高,導致船式拖拉機目前實際作業時驅動效率較低[3]。

許多學者從優化驅動輪結構角度出發對提高船式拖拉機直線作業性能展開研究。R.Beinstein[5]對拖拉機與土壤相互作業過程進行研究,得到了拖拉機接地壓比與車輪下陷量之間的關系。王修斌分析了輪刺受力,對葉輪的滾動阻力和推進力進行了理論計算[5]。蔣崇賢通過理論分析和實驗對比得到了葉輪作業時驅動力和驅動效率的計算公式,并首次提出以驅動效率作為評價葉輪工作特性的綜合指標[6]。何家良設計了一種入土深度調節機構,改善了機耕船對不同泥角水田的適應性問題[7]。韓數豐、李振鏞研究了葉輪入土深度、葉片寬度對葉輪推進力的影響[8]。邵耀堅對葉片寬度、驅動面傾角、非驅動面傾角等結構參數對驅動輪和整機的牽引性能的影響進行了分析[9]。陸華忠、羅錫文通過自制土槽實驗得到了葉輪所受推進力、支撐力及其驅動效率隨葉輪轉角變化的規律[10]。張超、江昱等通過光滑粒子流體動力學法設計并研究了單折面葉輪的直線驅動性能,相比直面葉輪,折面葉輪的直線驅動性得到較大幅度提升[11]。

綜上可知,目前船式拖拉機相關研究主要是從優化船體和驅動輪結構出發,來提高船式拖拉機直線驅動性能;然而,船式拖拉機工作參數也是影響船式拖拉機直線驅動性能的重要因素,目前鮮有學者研究。為此,以項目組研制的HH709S船式拖拉機驅動輪輪葉尺寸為參考依據,設計并搭建土槽試驗,校核模型準確性后,基于離散元法研究單輪葉與土壤的直線作業機理,以輪葉入土角度、入土深度,前進速度為影響因素,以推進力和扭矩為評價指標,從土壤堆積流動角度揭示工作參數對船式拖拉機驅動輪單輪葉直線驅動性能的影響機理,探究工作參數對直線驅動性能的影響規律,并采用多因素法獲取直線驅動性能較優的船式拖拉機直線工作參數,最后通過單輪葉損耗功率間接驗證了優化結果的可靠性。

1 驅動葉輪結構及入土深度

1.1 驅動葉輪結構

驅動葉輪是船式拖拉機行走部件,主要由輪葉和輪轂組成。輪葉與土壤直接作用,提供驅動力。船式拖拉機田間作業時,輪葉受力可分為垂直于輪葉的法向力FN和沿輪葉切向方向的切向力FT,兩者的合力為F;F可分解為水平方向的推進力FP和豎直方向的支撐力FL。當驅動葉輪轉角為θ時,驅動葉輪結構及輪葉的受力如圖1所示。

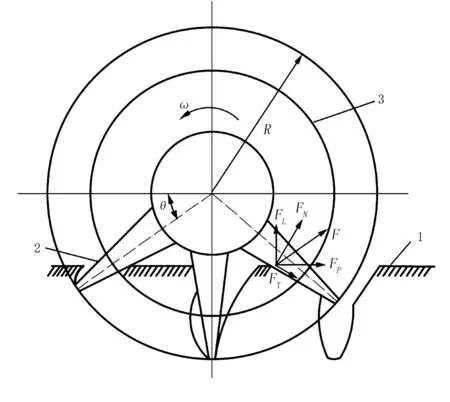
1.土壤表面 2.單輪葉 3.輪轂

1.2 入土深度

驅動葉輪的入土深度h是指輪葉運動直垂直狀態時土壤表面到輪葉最下端之間的距離,如圖2所示。入土深度影響輪葉受力,具體如下:入土深度較大時,輪葉受土壤反力較大,驅動能力強;但輪葉出土時挑土現象明顯,出土阻力也大,輪葉鏟泥和刮泥現象嚴重,導致驅動輪功率消耗較大,驅動效率低,工作性能差。入土深度較小時,輪葉與土壤間的作用力小,船體得不到足夠的驅動力,同樣也會導致驅動性能較差。在此,入土深度參考文獻[5]取h=220mm。為深入研究船式拖拉機與土壤作業機理,本文以單輪葉為例進行研究。驅動葉輪三維圖如圖2所示。

圖2 驅動葉輪三維圖Fig.2 Three dimensional diagram of driving impeller

2 離散元仿真

離散元法(DEM)自問世以來,在研究非連續介質力學問題上體現出無可替代的作用[12-13]。在研究農業機械與土壤相互作用時,有限元法難以準確模擬出土壤與機具相互作用時土壤流動和破裂的動態過程,導致設計方法與實際結果相差較大;而離散元法能夠更好地展示田間作業時農業機械受力和土壤的流動情況[14],故采用離散法對土壤進行建模。

2.1 土壤模型及性能參數測試

南方水田土壤含水率高、黏性強,為了更加準確模擬該土壤的物理特性,土壤顆粒之間的接觸模型選擇JKP接觸模型。該模型能夠考慮顆粒之間粘黏作用及土壤與葉輪輪葉之間的粘附作用,顆粒間的法向接觸力FJKR能夠根據顆粒間的重疊量、表面粘性力及接觸參數采用式(1)～式(4)進行計算。法向接觸力FJKR用來表示顆粒間的凝聚力[15-16],即

(1)

式中FJKR—法向彈性力(N);

E—等效彈性模量(Pa);

γ—表面能(J/m2);

R—等效接觸半徑(m);

α—切向重疊量(m)。

法向重疊量δ可由切向重疊量α換算得到,即

(2)

顆粒間最大間隙計算公式為

(3)

(4)

當顆粒并非實際接觸且間隔時間小于δc時,凝聚力達到最大值。凝聚力Fpull-out計算公式為

(5)

為設置土壤—單輪葉離散元計算模型的計算參數,對土壤相關參數進行了試驗測試。采用環刀法,經過多次測試得到土壤的密度值為1904kg/m3。采用SL-TSD型土壤測試儀,經過多次測量得到待測土壤含水率為28.58%。運用ZJ型無極調速應變控制式直剪儀多次測量并取其平均值,得到土壤內摩擦角φ=9.11°,內聚力c=12.9kPa。

圖3 實驗測試裝置Fig. 3 Experimental test device

2.2 土壤—單輪葉仿真模型搭建及驗證

葉輪的頂圓直徑為860mm,輪葉材料為45鋼,輪葉尺寸為240mm×180mm×6mm(寬×高×厚),驅動面傾角5°,非驅動面傾角4°,入土深度為220mm。土槽尺寸為1200mm×700mm×600mm(長×高×寬),選用直徑為8mm均勻球形顆粒模擬土壤,土壤顆粒材料屬性以及輪葉與土壤之間的接觸參數以前期土壤測試和相關文獻為參考依據得到具體數值,如表1所示[17-18]。單輪葉前進速度為2m/s,旋轉速度為5.81rad/s,滑轉率為20%,仿真時間為0.4s,數據保存間隔為0.001s。土壤與單輪葉離散元模型如圖4所示。

表1 仿真設置參數

圖4 單輪葉與土壤作用離散元模型Fig.4 Discrete element model of interaction between single blade and soil

單輪葉與土壤直線作業過程中,扭矩隨輪葉所轉角度的變化曲線如圖5所示。由圖5可知:扭矩在1個周期內呈現先升后降的趨勢。單輪葉入土后,隨著輪葉剪切和擠壓土壤增強,單輪葉扭矩增大;隨著輪葉繼續運動,推動土壤面積到達最大,扭矩逐漸降低。仿真結果中,單輪葉的扭矩從入土10.46N·m增大到222.084N·m,隨后逐漸降低。試驗結果中,扭矩從35.22N·m增大到251.86N·m,隨后逐漸降低。仿真結果與試驗結果扭矩的變化趨勢一致,且趨勢與文獻[19]的研究一致。試驗結果在數值上大于仿真結果的原因是由于仿真土壤與實際土壤的團體結構差異導致,由此證明了仿真模型的可靠性。

圖5 單輪葉扭矩隨轉過角度變化圖Fig.5 Variation of single blade torque with turning angle

2.3 單輪葉—土壤作業機理

單輪葉與土壤直線作業過程主要包括輪葉沿前進方向的直線運動和繞輪轂中心軸的旋轉運動。從輪葉接觸土壤到完全脫離土壤,輪葉所處的區域位置可分為入土區和出土區。其中,入土區為輪葉尖端從與土壤表面接觸到運動至最下位置的區段,出土區為輪葉尖端從最下位置運動到離開土壤的區段。為體現單輪葉與土壤直線作業過程,截取了仿真時間t=0s、t=0.005s、t=0.1s、t=0.16s、t=0.23s、t=0.27s時輪葉與土壤作業速度云圖,具體如圖6所示。

圖6 單輪葉與土壤作用過程的動力學仿真截圖Fig. 6 Dynamic simulation screenshot of interaction process between single blade and soil

t=0s時,單輪葉剛與土壤表面接觸,輪葉還未運動;t=0.05s時,輪葉開始進入入土區,對土壤開始產生擠壓和剪切作用,土壤顆粒被輪葉推動向左邊運動,輪葉受到水平向右的推進力,右邊顆粒微微隆起;t=0.1s時,單輪葉推動土壤顆粒個數增加,土壤顆粒速度變大,單輪葉向左邊擠壓土壤現象更加明顯,此時輪葉水平朝右的推力極劇增加;t=0.16s時,單輪葉狀態接近垂直,輪葉入土深度到達最大,向左邊推動的土壤顆粒個數到達最大值,顆粒速度相較t=0.1s時降低,輪葉即將進入出土區,開始出土;t=0.23時,輪葉進入出土區,開始出土,輪葉左邊挑土,輪葉右邊推土,此時因克服挑土會消耗一部分無用功率,推土導致土壤給輪葉推力方向變為水平向左,阻礙其出土;t=0.27s時,輪葉挑土顆粒個數到達最大值,輪葉向右推土現象更加明顯,土壤給其水平向左的推力更大,輪葉即將出土。綜上分析,為提高船式拖拉機驅動輪直線驅動性能,必須減小輪葉出土時克服挑土和推土的功率消耗,同時增加輪葉在入土區向左邊推動土壤顆粒個數的最大值,以此產生更大的驅動力。

對單輪葉與土壤相互作用進行求解計算,得到輪葉支撐力和推進力的具體數值,經換算得到輪葉支撐力和推進力隨著轉角的變化曲線,如圖7所示。

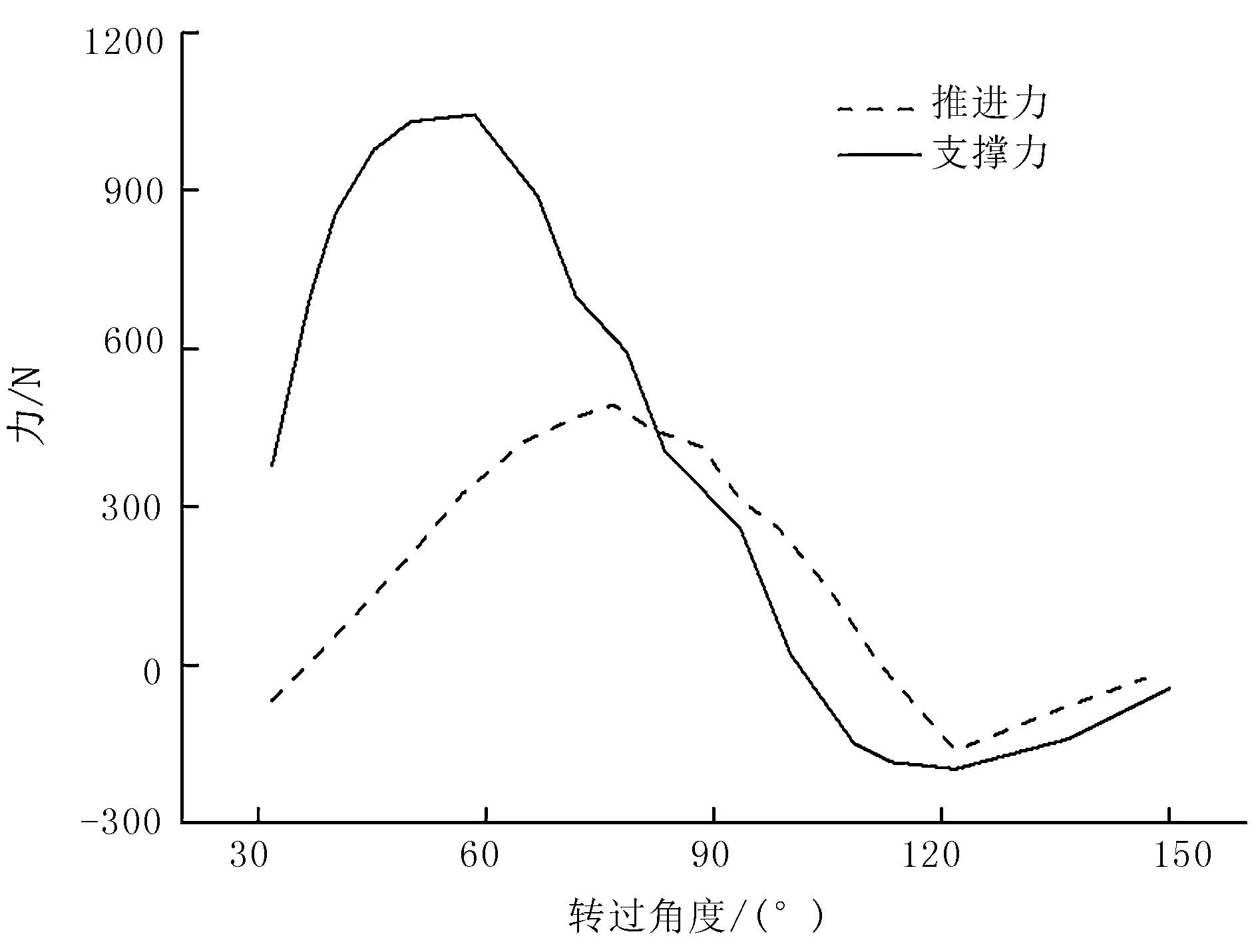
圖7 推進力和支撐力隨轉角的變化曲線Fig.7 Variation curve of propulsive force and supporting force with rotation angle

由圖7可知:輪葉在轉角為31°時開始接觸土壤,由于輪葉與土壤水平面夾角較小,輪葉所受總力在豎直方向的分力較大,且隨著入土深度的不斷變大,支撐力快速增加,在58°轉角時到達最大值,輪葉狀態如圖6(c)所示。隨著輪葉繼續運動,輪葉開始出土,支撐力開始降低,由于輪葉挑土,支撐力出現負值,在123°轉角時挑動土壤顆粒個數到達最大,支撐力負值達到峰值,此時輪葉的具體狀態如圖6(f)所示。直到輪葉完全出土,支撐力逐漸變為0。輪葉剛入土時,由于有較大的前進速度,輪葉會推動土壤向右運動,土壤給其反方向的推力,輪葉推進力為負值;隨著輪葉繼續入土,輪葉向左邊推動土壤面積逐漸增大,推進力逐步增加,但相較支撐力增加速度較慢,在轉角為79°時推進力到達最大值,輪葉的狀態如圖6(d)所示。在出土區,由于輪葉向前推土,推進力變為負值,隨著推土現象愈發明顯,推進力負值到達頂峰;隨后輪葉完全出土,推進力數值接近零值。對單輪葉所受推進力和扭矩進行計算,得到推進力為131.69N,扭矩為104.59N·m。

3 仿真試驗結果與分析

以單輪葉的入土角度、入土深度、前進速度為影響因素,探究工作參數對船式拖拉機直線驅動性能的影響規律,得到最佳的工作參數,以此提高船式拖拉機的直線驅動性能。

3.1 評價指標

1)推進力Fp。輪葉與土壤相互作用過程中,土壤對輪葉的反力為推進力,該力推動船式拖拉機向前行走或轉向,故其值越大,輪葉的驅動性能越好。

2)扭矩T。由實際工況可知,葉輪輪葉推進力Fp不可能無限增大,則引入輪葉轉向力矩T綜合評定輪葉的直線驅動性能:在Fp一定的前提下,T越大,船式拖拉機在轉向過程中的功率損耗就越大[20];在滿足船式拖拉機驅動葉輪直線驅動能力前提下,降低輪葉的扭矩能夠有效降低輪葉作業過程中的功率損耗,從而提高船式拖拉機的直線驅動性能。其中,T數值可直接從軟件中提取。

3.2 單因素仿真試驗

根據前期項目組自主研制的HH709S船式拖拉機工作參數的具體范圍[11,21-22],展開單因素仿真試驗,以探究入土角度、入土深度和前進速度對直線驅動性能的影響規律,尋找最佳的選取范圍。

圖8分別截取了單輪葉在不同入土角度、入土深度、前進速度下轉過角度為123°時的作業速度云圖。從宏觀角度分析單輪葉堆土和壓土現象,結合推進力和扭矩的變化規律,進而得到單輪葉直線驅動性能的優劣,如圖9～圖11所示。

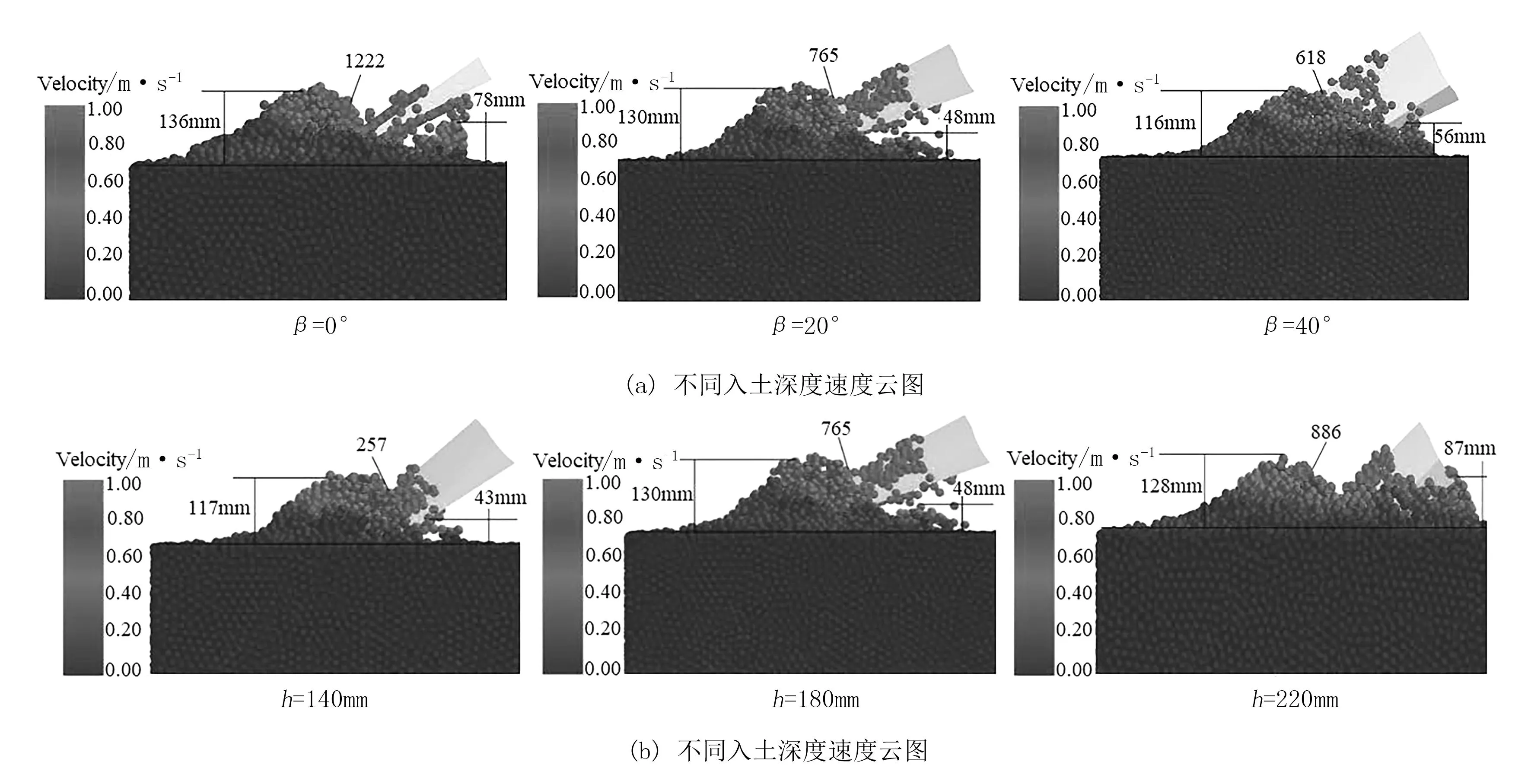
圖8 輪葉不同工作參數下速度云圖Fig.8 Cloud chart of speed under different working parameters of impeller

圖8(a)為當輪葉入土深度180mm、前進速度2m/s時不同入土角度輪葉的作業狀態圖。由圖8(a)可以看出:單輪葉與土壤直線作業時,由于輪葉對土壤的擠壓和推動作用,輪葉左右兩邊會產生一定大小的土堆,左邊土堆是由于輪葉從入土到出土整個過程中向左后方推動土壤以及出土時輪葉挑動土壤產生,且輪葉出土時速度較大,被挑動的土壤顆粒速度大。其中,左邊土堆一部分土壤顆粒在輪葉入土區已基本形成,土壤顆粒速度基本穩定且數值較小,這部分土壤顆粒給輪葉的反力與輪葉前進速度方向一致,水平朝右,推進力為正值;輪葉右邊土堆是由于輪葉出土時前進速度較大,擠壓土壤形成,這部分顆粒給輪葉的反力與輪葉前進速度方向相反,水平朝左,阻礙輪葉出土,推進力為負值。當輪葉入土角度從0°增加到40°時,左邊土堆高度從136mm降低到130mm,最后變為116mm,出土時挑動土壤顆粒個數分別為1222、765、618個,右邊土堆高度分別為78、48、56mm。由此表明:隨著輪葉入土角度的增加,輪葉水平朝右的推進力越來越大,輪葉出土時水平朝左的推進力先降低后增加,輪葉挑土現象越來越弱。

輪葉入土深度從140mm增加到220mm時,左邊土堆高度先從117mm升高到130mm再降低到128mm,挑土土壤顆粒個數分別為257、765、886個,右邊土堆高度分別為43、48、87mm。由此表明,隨著輪葉入土深度的增加,輪葉水平朝右的推進力先增加后降低,輪葉出土時水平朝左的推進力逐漸增加,輪葉挑土現象越來越明顯。

由圖(9)可知:當輪葉入土角度為20°時,推進力為197.69N,扭矩為95.74N·m;入土角度為40°時,推進力為146.1N,扭矩為90.28N·m;入土角度為0°時,推進力為176.09N,扭矩為89.04N·m。這是因為入土角度20°相較0°與土壤作業時輪葉左邊產生土堆高度相差不大,推進力正值相差不大;但入土角度為20°時右邊土堆高度更小,土壤阻礙作用小,推進力負值較小,推進力整體值最大;入土角度為40°時,由于左邊土堆高度下降幅度較大,推進力正值降低大,土壤阻礙作用較大,整體推進力最低。故輪葉入土角度的選取應在20°附近進行選擇,以保證輪葉推進力較大時,扭矩增幅不明顯。

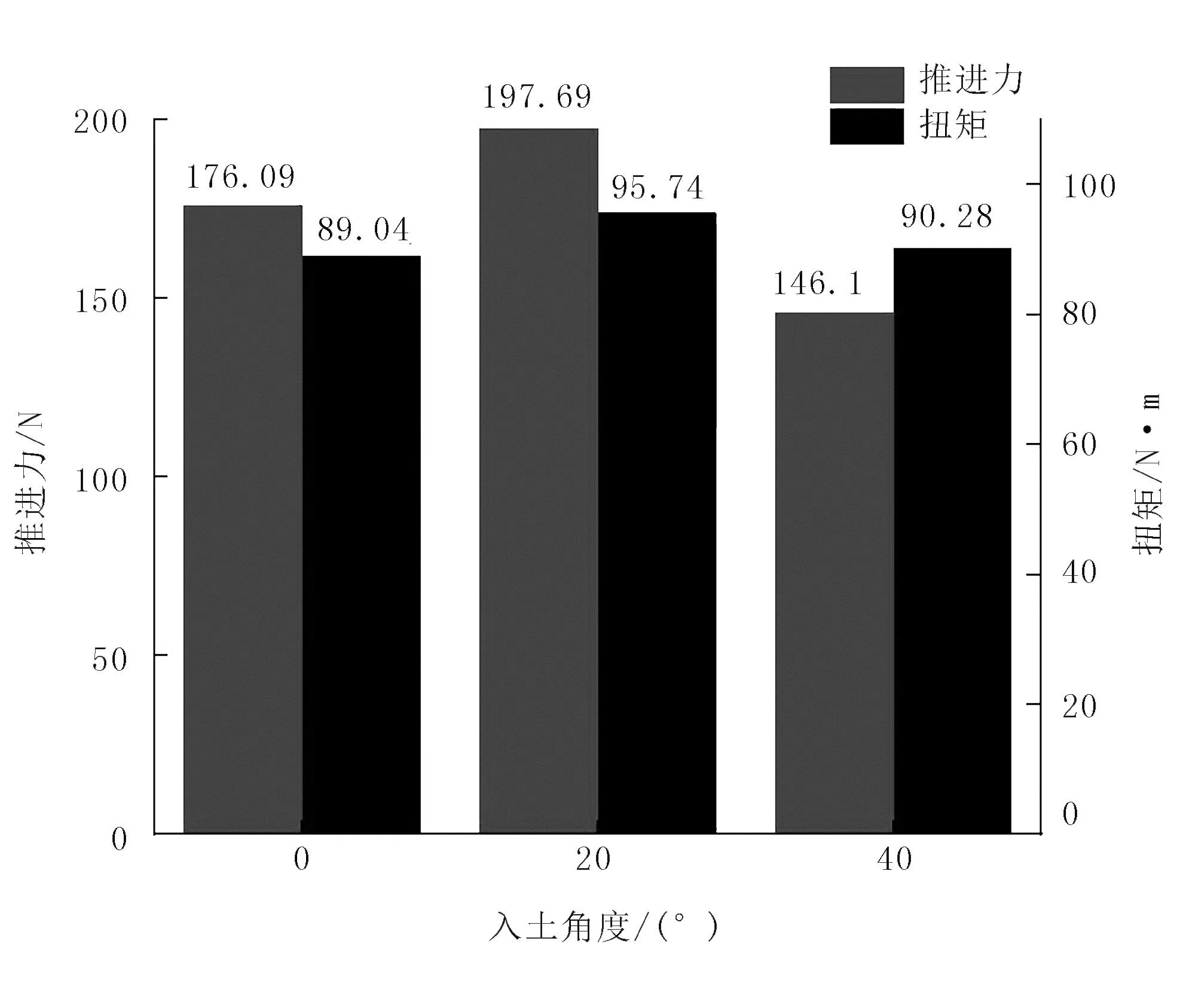
圖9 推進力和扭矩隨不同入土角度的變化規律Fig.9 Variation law of propulsive force and torque with different penetration angles

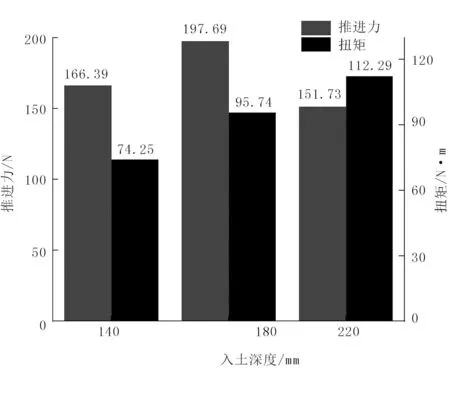
圖10 推進力和扭矩隨入土深度變化規律Fig.10 Variation law of propulsive force and torque with soil depth

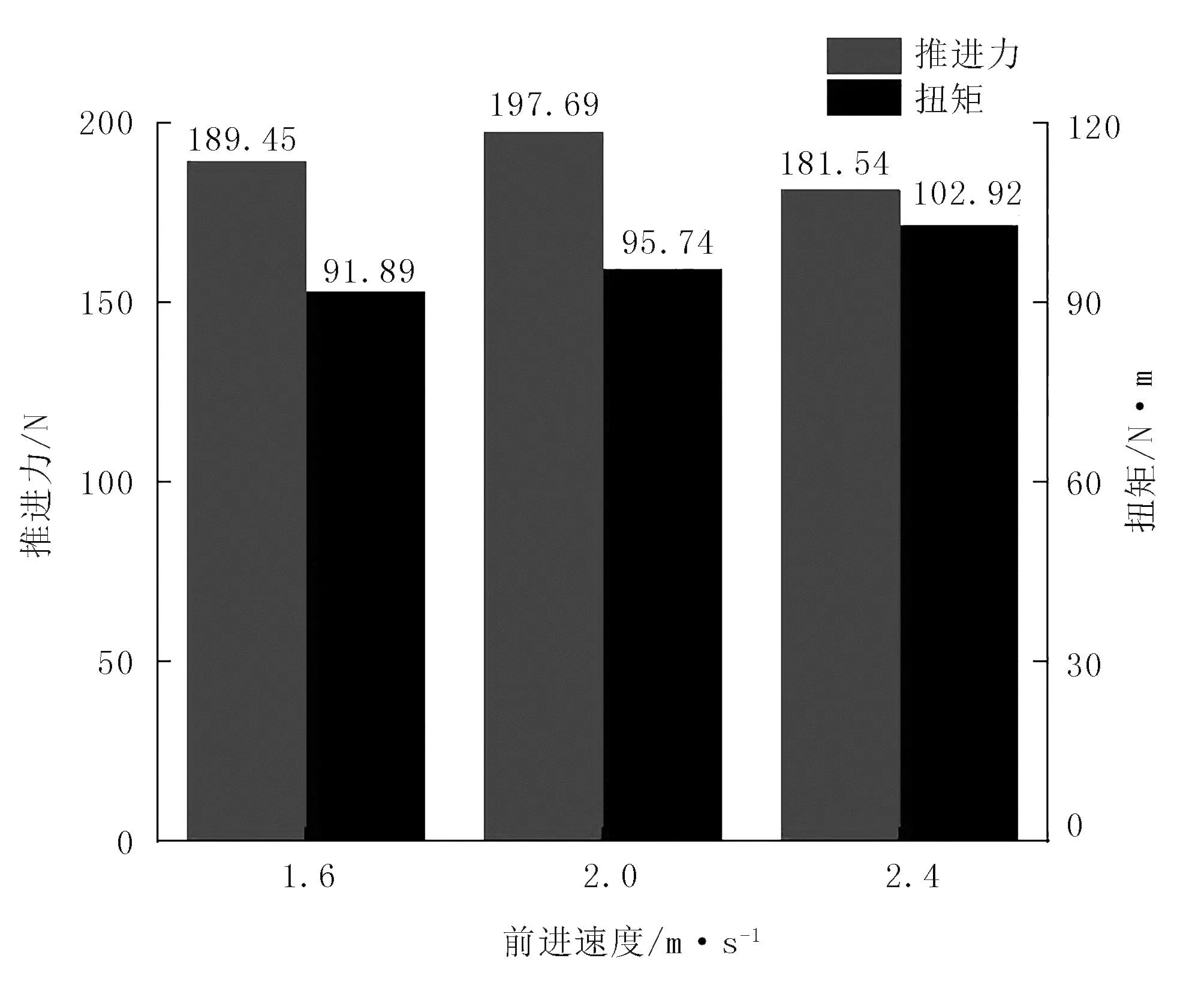
圖11 推進力和扭矩隨前進速度變化規律Fig.11 Variation law of propulsive force and torque with forward speed

由圖(10)可知:當輪葉入土深度為180mm時,推進力為197.69N,扭矩為95.74N·m;入土深度為220mm時,推進力為151.37N,扭矩為112.29N·m;入土角度為140mm時,推進力為166.39N,扭矩為74.25N·m。這是因為入土深度180mm相較140mm時與土壤作業時輪葉產生右邊土堆高度相差不大,輪葉出土時,土壤阻礙作用相當;但入土深度180mm時輪葉左邊產生土堆高度較140mm時高13mm,推進力正值漲幅較大,導致輪葉入土深度為180mm時整個過程推進力較大。入土深度為220mm時,雖然左邊土堆高度與180mm差距不大,推進力正值差別不大,但右邊土堆高39mm,輪葉出土時土壤阻礙作用最大,推進力負值最大,導致整個過程推進力最低,扭矩大。因此,輪葉入土深度既不能選擇太小導致推進力過小、驅動能力不夠,也不能選取太大導致輪葉出土時土壤對輪葉的阻礙作用過大、扭矩大、推進力小,直線驅動性能差。綜合以上分析,入土深度應在180mm附近選擇,既能保證推進力較大,且扭矩增加幅度不大,驅動性能高。

圖8(c)為輪葉入土角度為20°、入土深度為180mm時輪葉不同前進速度的作業狀態圖。由圖8(c)可知:當輪葉前進速度從1.6m/s增加到2.4m/s時,左邊土堆高度從132mm增加到626mm,挑土土壤顆粒數分別為543個、765個、626個,右邊土堆高度分別為69mm、48mm、58mm。這表明,隨著輪葉前進速度的增加,輪葉水平朝右的推進力越來越大,水平朝左的推進力先降低后增加,輪葉挑土現象越來越明顯。

由圖(11)可知:當輪葉前進速度為2m/s時,推進力為197.69N,扭矩為95.74N·m;當前進速度為2.4m/s時,推進力為181.54N,扭矩為102.92N·m;當前進速度為1.6m/s時,推進力為189.45N,扭矩為91.89N·m。這是因為前進速度2m/s相較1.6m/s輪葉左邊土堆高度相隔2mm,差別不大,推進力正值大小相當,但2m/s時右邊土堆高度小很多,土壤阻礙作用小,推進力負值小,導致2m/s相較1.6m/s輪葉整體推進力大、扭矩大。當前進速度為2.4m/s時,輪葉左邊土堆高度降低較大,推進力正值大幅度降低,輪葉右邊土堆增加,土壤阻礙作用增加,推進力負值增加,導致推進力降低幅度大較大。綜合以上分析,推進力與前進速度并不是正比關系,隨著前進速度的加大,推進力增加較小幅度后反而會下降,這與土壤的機械強度以及輪葉與土壤作用時間有關。故前進速度的選取應保證輪葉滿足一定驅動能力的推進力下,盡可能降低扭矩,在速度1.6m/s和2m/s之間選取較佳。

3.3 多因素仿真試驗

在保輪葉獲取較大推進力同時減弱扭矩,展開多因素正交試驗分析[23,24,25],以此求解單輪葉最佳的工作參數組合。根據編碼后的試驗方案分別建模并仿真,試驗因素編碼表如表2所示,試驗方案與結果如表3所示。

表2 試驗因素編碼

表3 正交試驗方案與結果

續表3

根據表3的試驗數據,通過Design-expert8.0.5軟件得到推進力和扭矩二次多項式回歸模型,即

FP=181.65-17.71A-20.72B+6.9C- 2.58AB+1.9AC-3.12BC-20.18A2-

36.96B2+2.97C2

(6)

T=90.9-2.86A+17.1B+6.27C+0.54AB+

0.43AC+2BC-4.81A2-3.54B2

(7)

分別對輪葉推進力和扭矩二次多項式模型進行方差分析,結果如表4和表5所示。

表4 推進力二次多項式模型的方差分析

表5 扭矩二次多項式模型的方差分析

由表4和表5可以看出:推進力和扭矩回歸模型的P值均小0.01,回歸模型高度顯著,擬合程度高。由入土深度、入土角度、前進速度的P值可以判斷3個試驗因素對單輪葉推進力和扭矩均產生較明顯影響。試驗因素對推進力的影響從大到小依次為入土深度、入土角度、前進速度,對扭矩的影響從大到小依次為入土深度、前進速度、入土角度。

利用Design-Expert軟件繪制各因素交互影響的3D響應曲面圖。入土深度和入土角度的響應曲面如圖12所示。入土角度從0°變化到40°時,推進力和扭矩均先增加后降低;入土深度從140mm變化到220mm時,推進力先增加后降低,扭矩一直增加;前進速度從1.6m/s變化到2.4m/s時,扭矩一直增加,這與4.2節中單因素研究結果一致。

3.4 參數優化結果

對正交試驗進行優化分析,在保證輪葉受推進力Fp較大的前提下,選取較小的扭矩,采用多目標變量優化方法[26]建立數學模型。采用響應面分析法對式(8)進行優化分析[27],計算結果表明:當輪葉入土角度為11°、入土深度為147mm、前進速度為1.6m/s時,單輪葉推進力最大為170.93N,扭矩相對最小為70.89N.m,單輪葉的直線驅動性能最佳。為驗證正交仿真求解結果的準確性,在最優工作參數組合條件下進行對比試驗,求得輪葉推進力為172.51N、扭矩為69.82N.m。推進力相對誤差為0.92%,扭矩相對誤差為1.5%,由此驗證了求解結果的可靠性,相對優化前單輪葉推進力提升了40.82N、扭矩降低了34.77N·m,直線驅動性能得到明顯提升。

(8)

4 試驗結果對比

土槽實驗平臺主要由盛土土槽、機架、滑輪導軌、驅動裝置、傳感器、傳動裝置、數據采集器、擋板等部件組成。盛土土槽具體參數為2m×1.4m×1m(長×寬×高)。卷揚機提供水平牽引力拉動機架,使單輪葉做勻速直線運動。交流伺服電機輸出動力,經減速器、扭矩傳感器、傳動軸使單輪葉進行旋轉運動。試驗前先連接所有工作部件。扭矩動態測控儀用24V電源供電,將扭矩動態測控儀用通信電纜與扭矩傳感器連接,用485USB線將扭矩動態測控儀與筆記本電腦的采集軟件相連接。輪葉裝配在傳動軸的套筒上,利用螺栓固定輪葉,具體如圖13所示。

圖13 土槽實驗裝置Fig.13 Soil tank experimental device

為驗證仿真所求工作參數的可靠性,通過數據采集軟件實時采集單輪葉與土壤直線作業過程中損耗功率間接來反映單輪葉直線驅動性能的優劣,將優化前后的損耗功率繪制成數據曲線,進行對比,從而確定優化結果的準確性,如圖14所示。

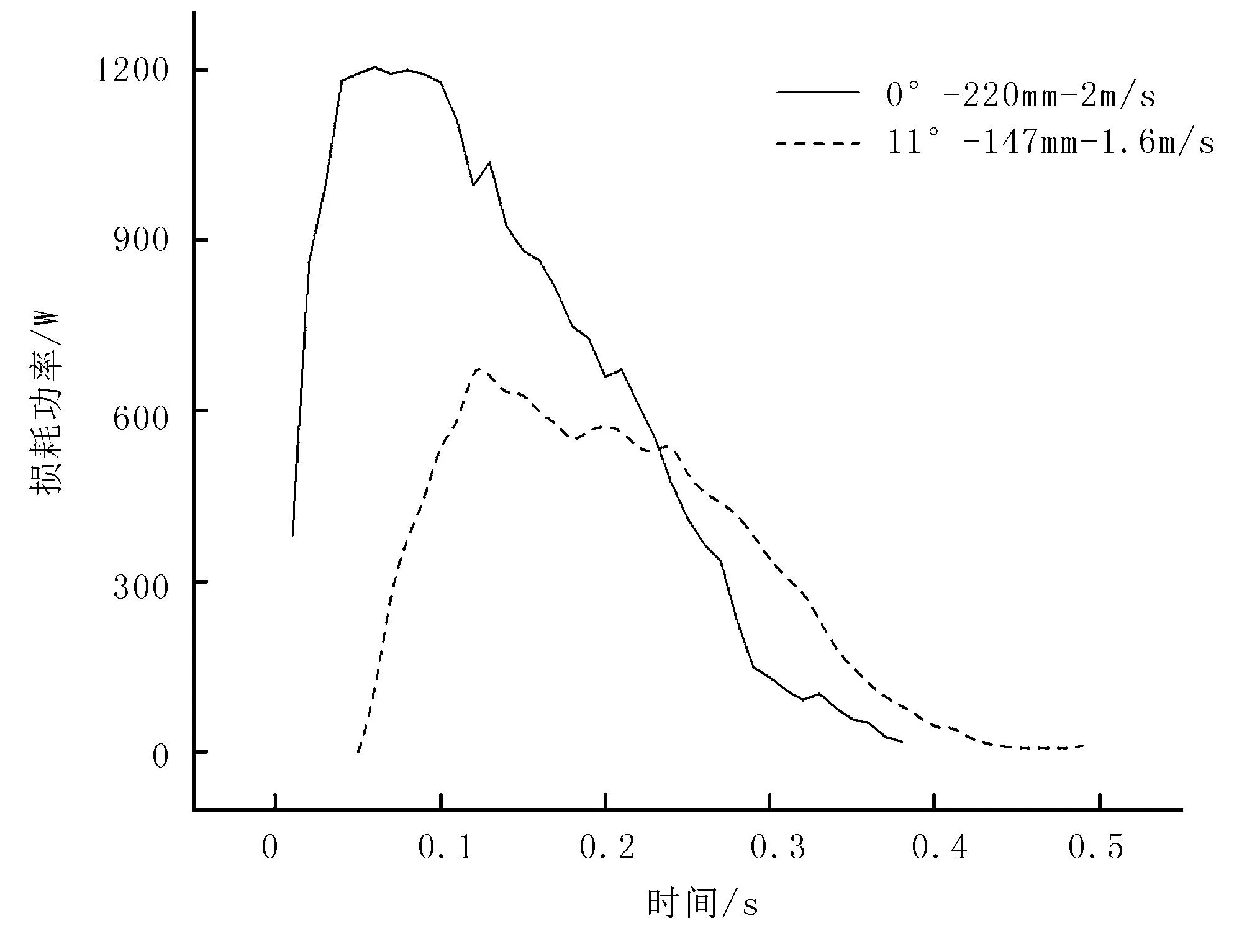
圖14 優化結果試驗驗證圖Fig.14 Test verification diagram of optimization results

由圖14可以看出:隨著輪葉與土壤直線作業,損耗功率均呈現先增加后降低的趨勢變化,單輪葉工作參數為11°-147mm-1.6m/s(優化后)相較0°-220mm-2m/s(優化前)損耗功率數值明顯降低。這表明,單輪葉工作參數為11°-147mm-1.6m/s時,單輪葉直線驅動性能優于優化前,間接證明了優化結果的準確性,同時再次驗證了本文所建立的土壤—單輪葉離散元模型的可靠性。

5 結論

1)構建了單輪葉—土壤離散元仿真模型和土槽試驗平臺,校核了仿真模型的準確性,分析了單輪葉與土壤直線作業機理,提出了評價單輪葉直線驅動性能的評價指標。

2)利用多因素法求解單輪葉直線作業的最佳工作參數為入土角度11°、入土深度147mm、前進速度1.6m/s,在此條件下單輪葉推進力明顯提高,扭矩明顯降低,單輪葉直線驅動性能最佳。

3)在最優工作參數組合下,單輪葉推進力為172.51N、扭矩為69.82N·m,優化前單輪葉推進力為131.69N、扭矩為104.59N.m,優化后推進力大幅度提高,扭矩降低明顯,單輪葉直線驅動性能得到提升。

4)通過土槽試驗對比了優化前后兩種工作參數下單輪葉損耗功率的具體情況,得到單輪葉在優化后工作參數下的損耗功率小。由此間接驗證了仿真求解結果的準確性,為船式拖拉機工作參數的選取提供了理論指導。