非視距環境下基于TOA 的移動目標定位

張 晨，王 剛

(寧波大學信息科學與工程學院，浙江 寧波 315211)

目標定位在近幾年來一直是研究熱點，也是無線傳感網絡(Wireless Sensor Networks，WSN)的重要任務。移動目標定位作為其中的一部分，在物流管理、車輛導航和緊急救援等領域都有著重要的應用[1-4]。

在移動目標定位場景中，傳感器采集目標發射電磁波的時間信息或頻率信息。常見的時間測量信息有:到達時間(Time-of-Arrival，TOA)[5-6]和到達時間差(Time-Difference-of-Arrival，TDOA)[7-10]；常見的頻率測量信息有:到達頻率(Frequency-of-Arrival，FOA)[5-6]和到達頻率差(Frequency-Difference-of-Arrival，FDOA)[7-8]。其中頻率測量依賴于物體的位置，加上物體移動速度未知，頻率測量比時間測量更加復雜[11]，因此本文采用時間測量的方法，它比頻率測量更加直接。定位的精度是需要關心問題，已有文獻討論基于時間測量的移動目標定位問題[12-14]，且取得了良好性能。但在實際的定位環境中，如城市中心，由于障礙物的遮擋，移動目標發射的電磁波往往需要經過多次反射或衍射才能到達錨節點，即傳播路徑是非視距的(Non-Line-of-Sight，NLOS)。在這種情況下，非視距傳播所引起的誤差對定位精度會產生很大的負面影響，而且已有文獻表明，非視距誤差通常遠大于測量噪聲[15]。此外，由于定位環境的不斷變化，所以非視距誤差的統計信息難以獲得，因此減少非視距誤差的影響在移動定位中就顯得格外重要。

對于非視距誤差的處理，已有很多文獻對其進行了研討。例如文獻[16-17]使用非視距誤差的統計信息來提高定位精度，但是在實際環境中，統計信息往往難以獲得。針對這種情況，文獻[15，18-21]提出了不需要已知非視距誤差的統計信息和路徑狀態的方法。一種是采用魯棒處理的方法，文獻[18]提出對非視距誤差做魯棒處理，將其轉化為最大最小問題，再利用二階錐松弛(Second-Order Cone Relaxation，SOCR) 和半正定松弛(Semidefinite Relaxation，SDR)技術對其進行處理。這種方法僅要求已知非視距的誤差上界。然而，當測量環境為視距時，已知的上界通常太大，導致這種方法在稀疏非視距環境中沒有很好的性能。另一種是采用估計處理的方法，文獻[15]提出了聯合估計源位置和與非視距誤差有關的平衡參數的方法，并通過SOCR和SDR 對問題進行松弛，從而緩解了非視距誤差的影響。文獻[19]提出了非視距環境下協作定位，對源位置和非視距差的二次多項式進行估計，并通過SDR 對問題進行松弛。而文獻[20-21]采用估計處理和魯棒處理結合的方法，聯合估計源位置和與非視距誤差有關平衡參數，同時對新的變量做魯棒性處理。在估計的方法中，若直接對所有的非視距誤差進行估計，會涉及到大量的優化變量，意味著需要大量的精確測量來估計所有的參數，這在密集的非視距環境下，會由于測量不精確導致性能下降[20]。

本文研究了非視距環境下基于TOA 的移動目標定位問題。WSN 中的錨節點對移動目標進行多次采樣得到多組TOA 測量值，每組均含有測量噪聲和非視距誤差。對測量數據采用估計的方法，但如果直接估計移動目標的初始位置、移動速度和所有的非視距誤差，在采樣點多的情況下，模型會涉及到大量的優化變量，從而導致精度下降。因此對于非視距誤差不進行直接估計，參考文獻[19]的方法，將非視距誤差的一次項和二次項進行組合，再加上合理的近似，對其整體進行估計，這樣優化變量的數目便可減少。接著在此基礎上，推導出約束最小二乘(Least Squares，LS)問題，這是一個非凸的問題，通過SDR 將其松弛為凸的SDP 問題，該方法不需要知道非視距誤差上限和路徑狀態。通過對算法的仿真與分析，發現在密集和稀疏的非視距的環境下，本文提出的方法都取得了良好的性能，從而有效減輕了非視距誤差產生的負面影響。

本文的章節內容組織如下。第一節描述了基于TOA 的移動目標定位場景；第二節詳細闡述了構造約束LS 問題并將其松弛為凸的SDP 問題的推導過程；第三節通過仿真給出了算法的性能分析并探究了懲罰因子對算法敏感度的影響；第四節給出結論。

文本采用的符號說明如下。向量和矩陣分別用粗體小寫字母和粗體大寫字母表示。ai表示向量a中第i個元素；A(i，j)表示矩陣A中第(i，j)個元素。a(1:i)表示向量a中第1 到第i個元素所構成的子向量；A(1:i，1:j)表示矩陣A中第1 到第i行，第1 到第j列所構成的子矩陣。0k×l代表k行l列的全零矩陣。tr(A)和rank(A)分別表示矩陣A的跡和秩；A≥0表示矩陣A是半正定的。?k表示k維實空間。

1 問題描述

考慮一個k(k＝2 或3)維場景上的移動目標定位問題。如圖1 所示，設WSN 中有N個已知的錨節點和1 個未知的移動目標，其中第i個錨節點的坐標用si∈?k(i＝1，2，…，N)表示，移動目標初始位置的坐標用x∈?k表示，移動速度用v∈?k表示，每個錨節點對移動目標的采樣點數為M，且采樣周期為T。假設T的數值很小，則可以認為移動目標在整個過程中速度保持不變[21]。

圖1 移動目標定位場景

設錨節點和移動目標之間存在著測量噪聲和非視距誤差，則相應的TOA 測量模型如下所示:

式中:c是光速，nij/c是第i條路徑上進行第j次采樣時的測量噪聲。假設T的數值很小，則錨節點和移動目標之間的信號傳播路徑基本不變，于是可以認為錨節點M次采樣時的非視距誤差均相等，于是用ei/c來代表第i條路徑上每次采樣到的非視距誤差。將式(1)兩端同時乘以c，則相應的測量模型轉化為如下所示:

通常假設nij是服從均值為零，方差為的高斯分布。ei是取值為正的非視距誤差，由于真實環境在不斷變化，所以它的分布往往難以獲得，通常只假設它的上限為ρi，即0≤ei≤ρi。這里還要指出，測量噪聲往往比非視距誤差小很多，即ei?nij，從而非視距誤差在移動目標定位中需要格外關注[15]。

2 半正定規劃問題的構造

在本節中，首先在式(2)的基礎上推導并構造出約束LS 問題，然后對其進行松弛，轉化為易于處理的凸的SDP 問題，從而完成對移動目標的初始位置和移動速度的估計。

首先將式(2)中的ei移到等式左邊，并對等式兩端進行平方，得到的結果如下所示:

對式(3)的兩端展開并移項，可得:

式中:測量噪聲的二次平方項被忽略，因為其數值上遠小于‖x+jTv-si‖2[15]，而非視距誤差的二次項不能被忽略。

對于非視距誤差的處理，采用估計的方法。式(4)中含有非視距誤差的一次項2dijei和二次項。為了減少優化變量的數目，在T不大的情況下，非視距誤差一次項中的dij可以近似用第i條路徑M次采樣的平均值來代替:

令ci＝2ei-(i＝1，2，…，N)，即用ci代替非視距誤差一次項和二次項的整體，則對非視距誤差的估計轉化為了對ci(i＝1，2，…，N)的估計。本文將ci作為變量與移動目標初始位置x和移動速度v進行聯合估計。由此定義，式(4)可轉化為:

進一步，令u＝‖x‖2，w＝‖v‖2，z＝xTv。并且令c＝[c1，c2，…，cN]T，則式(6)可寫為:

根據式(8)，可以構造如下約束LS 問題:

問題(10)仍是一個非凸問題，難以求解。本文通過SDR 將其松弛為SDP 問題。為此，引入矩陣Y并令Y＝yyT，則約束(10a)-(10c)分別可以表示成如下形式:

則問題(10)可以轉化為:

通過引入:

再結合如下的等價變換:

則問題(12)可以轉化為:

在問題(15)中，唯一的非凸約束是rank(Y)＝1這一項，將其舍棄，則問題(15)可以轉化為如下凸的SDP 問題:

為了使松弛后的SDP 問題更加收緊于原問題，需要引入一些額外的約束項。注意到:

因為nij?‖x+jTv-si‖，且ei≥0，所以容易得到ci≥0，并且有如下的等價表示:

于是本文在問題(16)中引入約束(18)來進行收緊。而且為了避免問題(16)中ci的解太大，我們對其增加一個懲罰項來抑制ci的值。于是得到最終凸的SDP 問題:

式中:λ為懲罰因子。求解問題(19)，便可以得到移動目標的初始位置估計和移動速度估計。本節最后給出算法的偽代碼，用來總結所提出的方法，具體如算法1 所示。

算法1 移動目標定位的SDP 算法

3 仿真與分析

3.1 算法復雜度分析

通常解決混合SDP/SOCP 問題的復雜度為:

式中:m是等式約束的個數，NSD和NSOC分別是半正定錐約束和二階錐約束的個數，分別是第i個半正定錐和二階錐的維度，μ＝為壁壘參數，用來測量所涉及錐的幾何復雜度，ε＞0是解的精確度。下文用“SDP-NLOS”來指代本文所提出的方法，該方法有4 個等式約束[(11a) -(11c)，(18)]，有1 個維度為2k+N+4 的半正定錐約束[(15a)]，二階錐約束的個數和維度均為零，所以SDP-NLOS 最壞情況下的復雜度為O[4(2k+N+4)3.5ln(1/ε)]。為了和文本提出的方法形成對比，文章綜合文獻[20-21]對非視距誤差的處理方法:魯棒處理和估計處理結合的方法，并將其拓展到移動目標定位問題上，且將其命名為“RSDP”(魯棒SDP)，具體推導過程見附錄。該方法有NM+4 個等式約束[(34b)，(38e)，(38f)]，有3 個半正定約束[(33)，(38a)，(38b)]，維度分別為NM+1、2k+1 和NM+2，二階錐約束的個數和維度均為零，所以RSDP 最壞情況下的復雜度為O[(NM+2)4.5ln(1/ε)]，可以發現，本文提出算法的復雜度明顯低于RSDP，且隨著采樣點數的增加，這種效果更加明顯。

3.2 仿真結果

在本小節中，通過軟件仿真對本文所提出的方法進行性能測試與分析。為了進一步體現SDPNLOS 對非視距誤差的緩解作用，本文在問題(19)的基礎上舍棄非視距誤差的一次項2dijei和二次項，得到不考慮非視距誤差的SDP 問題:

矩陣A、B和常數r的形式同(13a)-(13c)，下文將該算法命名為“SDP”。

為了對比分析SDP-NLOS、SDP 和RSDP 的定位性能。本文通過MATLAB R2017a 軟件進行仿真，求解工具箱采用CVX，求解器為Sedumi。首先設置維數k＝2，采樣周期T＝0.6 s，SDP-NLOS 中懲罰因子λ＝0.1，并且根據文獻[20-21]，設置RSDP 中的取ρij平均值的一半，即:

然后在表1 中給出各個錨節點的坐標。

表1 錨節點坐標

移動目標在[-25 m，25 m]×[-25 m，25 m]的正方形區域內隨機產生50 個，而且每個移動目標x軸方向的移動速度vx和y軸方向的移動速度vy均在-2 m/s～2 m/s 之間隨機產生。最后根據式(2)生成含噪聲的TOA 測量值，其中測量噪聲由高斯分布產生，令＝σ2，則nij～N(0，σ2)，其中非視距誤差由均勻分布產生，令ρi＝ρ，則ei～U(0，ρ)。

移動目標的定位性能用均方根誤差(Root Mean Square Error，RMSE)來衡量。對初始位置x估計的RMSE 和對移動速度v估計的RMSE 分別定義為:

式中:和分別是估計出的初始位置和移動速度，xi和vi分別是真實的初始位置和移動速度，M為蒙特卡洛仿真次數，設置每個移動目標仿真500次，又因為有50 個移動目標，所以M＝25 000。下文考慮五種仿真場景，在場景一到四中，每條路徑狀態(視距或非視距)都是隨機選取的，且每條路徑屬于非視距的概率均設置為50%[20-21]。需要指出的是，RSDP 需要知道非視距誤差的上限，而SDP-NLOS和SDP 不需要知道誤差的上限。

場景一:改變非視距誤差上限ρ＝1，2，…，6，考慮非視距誤差對移動目標定位的影響。設置錨節點的個數N＝5，編號為1～5，每個錨節點的采樣點數M＝4，測量噪聲的標準差σ＝0.1。初始位置估計的仿真結果如圖2(a)所示，移動速度估計的仿真結果如2(b)所示。能夠發現隨著非視距誤差上限的增加，三種方法對于移動目標的定位性能均有所下降，其中SDP-NLOS 與RSDP 相比，在移動速度的估計上沒有明顯的差異，但在初始位置的估計上有著明顯的優勢。具體地，當ρ＝6 時，SDP-NLOS 和RSDP相比在初始位置的估計上有0.3 m 左右的優勢。由于SDP 未考慮非視距誤差的影響，因此SDP 對于位置和速度的估計均是最差的。綜合分析，本文提出的方法SDP-NLOS 更有優勢。

圖2 非視距誤差上限變化時的性能比較

場景二:改變測量噪聲的標準差σ＝0.1，0.2，…，0.6，考慮測量噪聲標準差對移動目標定位的影響。設置錨節點的個數N＝5，編號為1～5，非視距誤差上限ρ＝5，每個錨節點的采樣點數M＝4。初始位置估計的仿真結果如圖3(a)所示，移動速度估計的仿真結果如圖3(b)所示。能夠發現，隨著噪聲標準差的增加，三種方法對于移動目標的定位性能均有所下降，SDP-NLOS 與RSDP 相比，在移動速度的估計上有平均0.03 m/s 的劣勢，但在初始位置的估計上有平均0.23 m 的優勢。而SDP 對于兩者的估計是最差的。綜合位置和速度的分析，本文提出的方法SDP-NLOS 更具有優勢。

圖3 噪聲標準差變化時的性能比較

場景三:改變錨節點個數N＝4，5，…，9，考慮錨節點個數對移動目標定位的影響。設置非視距誤差上限ρ＝5，測量噪聲的標準差σ＝0.1，每個錨節點的采樣點數M＝4。初始位置估計的仿真結果如圖4(a)所示，移動速度估計的仿真結果如圖4(b)所示。能夠發現，隨著錨節點個數的增加，三種方法對于初始位置和移動速度估計的RMSE 均有所下降，這是因為隨著錨節點個數的增多，獲取到的信息會增多，對位置和速度估計的精度就會提高。其中SDP-NLOS 對兩者估計的性能最優，RSDP 的性能次之，SDP 的性能最差。

圖4 錨節點個數變化時的性能比較

場景四:改變采樣點數M＝2，3，…，7，考慮采樣點數對移動目標定位的影響。設置錨節點的個數N＝5，編號為1～5，非視距誤差上限ρ＝5，測量噪聲的標準差σ＝0.1。初始位置估計的仿真結果如圖5(a)所示，移動速度估計的仿真結果如圖5(b)所示。能夠發現，隨著采樣點數的增加，提出的方法對于移動目標的定位性能提高，這是由于當采樣點數增加時，相應得到的方程數就會增加，對位置和速度估計的精度就會提高。其中SDP-NLOS 更占有優勢。具體地，SDP-NLOS 和RSDP 相比，在初始位置的估計上有平均0.32 m 的優勢，在移動速度的估計上兩者無明顯差別。同樣地，SDP 對于兩者的估計是最差的。

圖5 采樣點數變化時的性能比較

場景五:通過改變非視距路徑的個數Nnlos＝0，1，…，5，考慮路徑狀態對移動目標定位的影響。設置錨節點的個數N＝5，編號為1～5，每個錨節點的采樣點數M＝4，非視距誤差上限ρ＝5，測量噪聲的標準差σ＝0.1。初始位置估計的仿真結果如圖6(a)所示，移動速度估計的仿真結果如圖6(b)所示。具體地，當所有路徑均為非視距時，由于RSDP 做了魯棒性處理，因此性能優于提出的方法SDP-NLOS，但當視距路徑的比例大于1/5 時，SDP-NLOS 的性能優于RSDP；由于SDP 未考慮非視距誤差的影響，因此SDP對于兩者的估計在大多數情況下是最差的。可以發現，本文提出的方法SDP-NLOS 能應用于視距和非視距同時存在的場景，且定位效果良好。

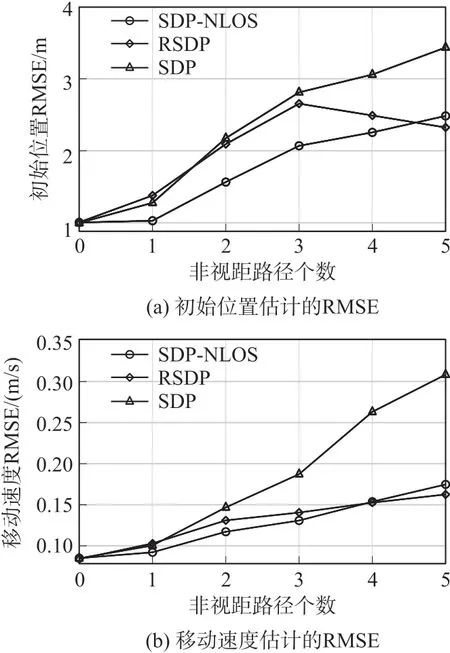
圖6 非視距路徑的個數變化時的性能比較

3.3 懲罰因子對算法敏感度的影響

通過改變懲罰因子λ，來觀察不同的λ對SDPNLOS 敏感度的影響，這樣能在實際的場景下，為λ的選取提供參考。設置錨節點的個數N＝5，編號為1～5，每個錨節點的采樣點數M＝4，非視距誤差上限ρ＝2，測量噪聲的標準差σ＝0.1。在此場景下改變λ，得到的結果如圖7 所示。可以發現當λ≥0.01時，對初始位置估計的RMSE 大約在1.23 m～1.38 m之間，波動幅度不大。而對移動速度估計的RMSE 大約穩定在0.098 m/s 左右，基本無變化。因此該方法對λ變動的敏感度較低，從而使λ的選取有著較大的范圍。

圖7 懲罰因子λ 變化時，初始位置估計的RMSE變化和移動速度估計的RMSE 變化

4 總結

本文基于TOA 的測量方法研究了非視距環境下移動目標的定位問題。為降低非視距誤差的影響，本文采用估計的方法，構造了約束LS 問題，實現了對移動目標的初始位置、移動速度和非視距誤差的聯合估計。并通過合理的近似，使優化變量的數目得以減少，以增加模型求解的準確程度。本文對該問題進行松弛，轉化為了凸的SDP 問題，并通過仿真證實了該方法在稀疏和密集的非視距環境下均有著良好的性能。本文提出的方法不需要知道非視距誤差上限，且在算法復雜度上有著明顯的優勢。

附錄 RSDP(魯棒SDP)的推導

文章綜合文獻[20-21]對非視距誤差的處理方法，并將其拓展到非合作式移動目標定位問題上。

針對移動目標的距離測量值可以寫成下式所示:

根據式(26)，有如下的魯棒約束最小二乘問題，其中對目標位置x，移動速度v和平衡參數做估計處理，對產生新的變量做魯棒處理:

將問題(28)寫成上鏡圖的形式:

通過S-Lemma，式(30)可以轉化為存在λ≥0使得:

則問題(29)可以轉化為如下所示:

問題(34)仍是一個非凸問題，難以求解。下面通過SDR 將其松弛為SDP 問題。為此引入矩陣G并令G＝ggT，引入向量y＝[xT，vT]T∈?2k和矩陣Y，并令Y＝yyT，則q可以表示為:

再結合如下的等價變換:

則問題(34)可以轉化為如下的SDP 問題:

在問題(38)中，非凸約束是矩陣的秩等于1 的約束，現將其舍棄，則問題(38)最終可以轉化為如下凸的SDP 問題:

綜上所述，問題(39)便是綜合文獻[20-21]后產生的非合作式移動目標定位問題，即正文中的RSDP(魯棒SDP)方法。