基于碳酸鹽環境的甲基三辛基碳酸銨萃取鈾的分配比模型

方豪凡, 何明鍵, 矯彩山, 張萌, 王靖陽

(哈爾濱工程大學 核科學與技術學院,黑龍江 哈爾濱 150001)

隨著核能的持續發展,管理每年產生的大量乏核燃料已成為限制核能發展的主要因素之一[1]。PUREX流程由于其優越的性能是目前唯一用于商業應用的乏燃料后處理流程,但該流程仍然存在無法解決的問題[2-3]。如硝酸溶液對設備的腐蝕、有機溶劑的輻射分解、產生的放射性廢物種類多、高放廢液難于處理等[3-5]。基于碳酸鹽環境的CARBEX流程采用碳酸鹽-過氧化氫溶解乏燃料,并使用季銨鹽萃取分離關鍵核素[6-8]。由于此流程不使用硝酸,對設備腐蝕性小,流程的安全性更高,并且在整個流程中不產生氮氧化物等氣態污染物;此外,由于大量的裂片元素不會溶解在碳酸鹽溶液中,溶解液的放射性水平遠低于PUREX的酸性溶解液;同時由于季銨鹽類萃取劑具有更好的耐輻照穩定性,可避免因有機溶劑的輻解等而產生第三相的問題,萃余液組分也相對簡單。所以,此流程特別適合于高燃耗、短冷卻期乏燃料的后處理[9-10]。

相較于CARBEX流程,PUREX流程的研究更為系統,已建立了成熟的分配比模型用于指導萃取反應器的設計。在PUREX流程分配比模型數學函數的研究中,Richardson[18]建立了的萃取體系中各種組分分配比D數學模型,將表觀平衡常數表征為總鹽濃度的函數,從而將D關聯成為自由[TBP]free濃度與總鹽濃度的函數。而Geldard[19]則將表觀平衡常數表征為離子強度的函數,從而將分配比D與水相離子強度相關聯,建立了PUREX流程的分配比模型函數。他們所建立的分配比模型均可以準確地反映萃取反應,在PUREX流程模擬方面有廣泛的應用,世界上主要核技術國家的PUREX流程計算機模擬軟件大多以此2種模型為基礎。萃取分配比模型是建立后處理工藝流程計算機模擬研究的關鍵[20-23],但CARBEX流程的相關研究還較為基礎,目前都集中于各影響因素對萃取分配比影響趨勢的探究,并沒有建立分配比數學模型。

1 萃取反應機理

CARBEX流程使用碳酸鹽水溶液介質,在萃取過程中不宜引入新的雜質離子,因此采用MTOAC作為萃取劑是最合適的,MTOAC的結構如圖1所示。

圖2 MTOAC與鈾結合后的結構簡式(MTOAU)Fig.2 The structure of MTOAC combined with uranium (MTOAU)

MTOAC為離子締合體,會發生聚合現象,在此體系中聚合度為2,結合文獻[16],可以得出萃取反應方程式為:

(1)

2 分配比模型的建立

(2)

將式(2)進行變量分離,可以得到:

(3)

式中cUR/cU為萃取平衡時的分配比D。對于反應的平衡常數,在溫度恒定時為常數,而4個活度因子均與離子強度相關,離子強度I的函數K*為:

(4)

分析得出K*=f(I)=f(cC0,cU),同時,式(2)簡化為:

f(cC0,cU)·cR=D

(5)

2.1 f(cC0,cU)項的確定

根據分配比定義,D=cUR/cU,而f(cC0,cU)也是與cU關聯的函數,導致了式(5)中的等號兩邊均存在cU,因此需要將等號左邊轉化成與cU無關。分析前期實驗數據cR0=30%,25 ℃,A/O=1∶1,得出不同水相碳酸根濃度時,初始水相鈾濃度和平衡時水相鈾濃度的關系,如圖3所示。

從圖3可以看出,cU0與cU存在線性關系,但斜率隨著cC0的增加而增加,cU=f(cU0,cC0),所以f(cC0,cU)=f(cU0,cC0)。若假設cR為常數,則分配比D只與cU0和cC0有關。重新將圖3轉換為不同水相碳酸根濃度時,初始水相鈾濃度與分配比的圖,如圖4所示。

圖4 不同cC0條件下,cU0與D關系圖Fig.4 The relationship between cU0 and D under different cC0 conditions

使用y=ax-b函數對圖4中數據擬合,可以得出在不同的cU0下,a和b的值如表1所示。

表1 不同的cU0下,a和b的擬合值Table 1 The fit values of a and b for different cU0

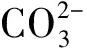
(6)

2.2 cR項的確定

cR為平衡狀態下有機相中自由的MTOAC濃度,cR=cR0-cUR。

另外定義參數值相比A,A=Vorg/Vaq,Vorg為有機相體積,Vaq為水相體積。相比并不會直接影響反應平衡,也不會影響cU0、cC0、cR0和cUR0這4個初始值,但是卻影響了反應產物的量,因此會影響cUR和cU。由于cUR和cU本身就存在一定的聯系,為了方便擬合,本文在2.1節中未考慮相比的影響,而是將相比的影響都歸于cR項。因此可以得出:

cR=f1(cR0)·f2(A)

(7)

2.2.1f1(cR0)函數的確定

由于前面的擬合都是基于相比A=1的條件下進行的,因此本文設定A=1時,f2(A)=1。因此式(6)可以變換為:

(8)

圖5為cR0和f1(cR0)的關系圖,使用二次函數擬合得到:

圖5 cR0和f1(cR0)關系Fig.5 The relationship between cR0 and f1(cR0)

f1(cR0)=-13.46(cR0-0.445)2+2.522

(9)

該擬合的R2=0.969 8,擬合效果較好。同時式(9)中的方程存在最大值,即cR0=0.445 mol/L處,f1(cR0)達到最大值,近似為MTOAC作為萃取劑時的飽和濃度,證明MTOAC確實存在聚合效應,聚合度為2。由于大部分實驗是在MTOAC濃度為30vol%的條件下做的,考慮MTOAC粘度較高并且要保證有機相飽和萃取容量,通過實踐表明30vol%的濃度也是最適合CARBEX流程的萃取劑濃度,因此在計算中若使用的也是30vol%的MTOAC,可以簡化為f1(cR0)≈1。

2.2.2f2(A)函數的確定

同樣采用類似2.2.1節的方式,對式(6)進行變換:

(10)

由于2.2.1節中使用了f2(1)=1的設定,所以擬合f2(A)時,該擬合曲線應該通過點(1,1)。繪制A和f2(A)的關系如圖6所示。

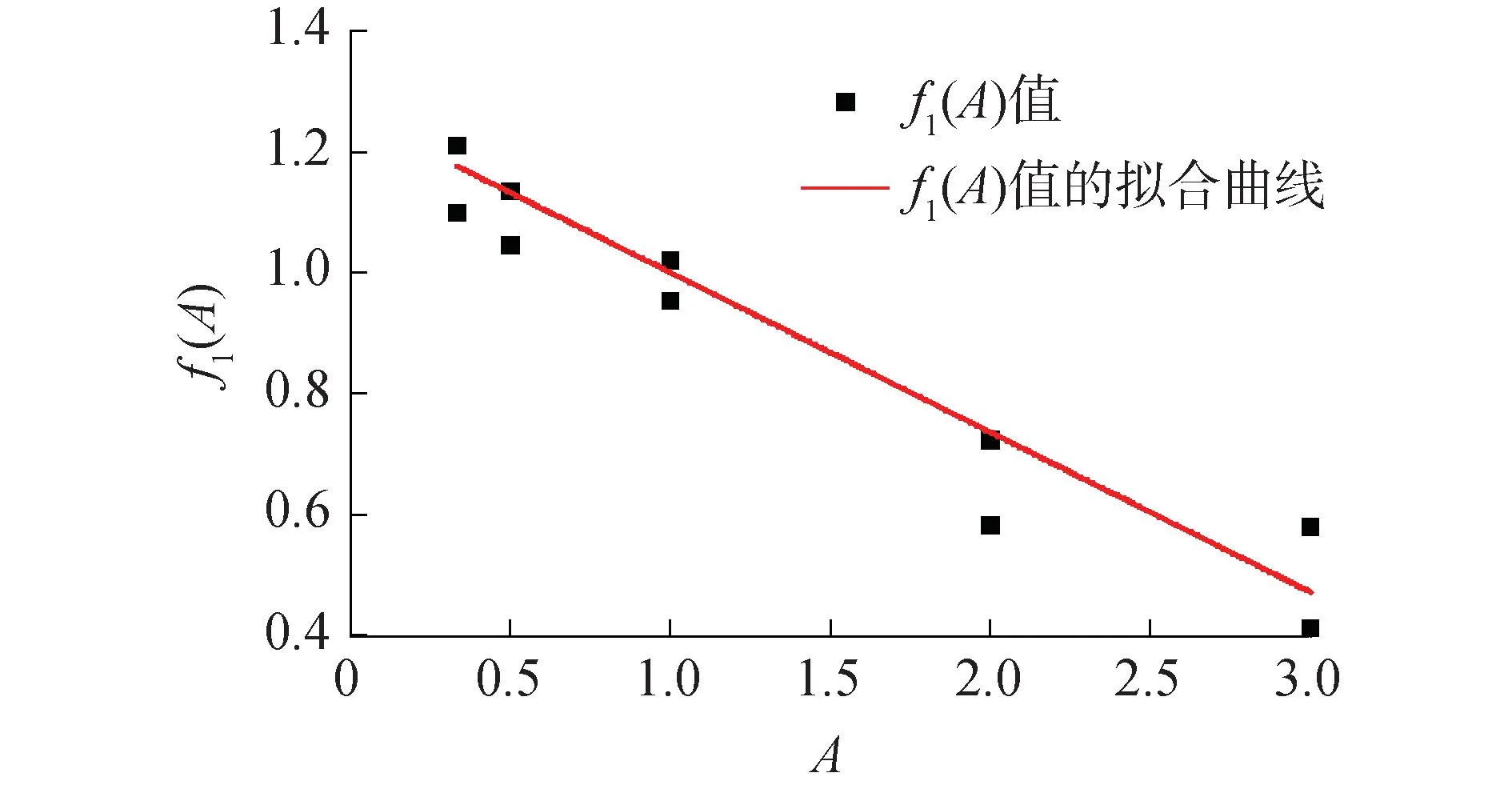
圖6 A和f2(A)的關系Fig.6 The relationship between A and f2(A)

用線性函數擬合得到:

f2(A)=-0.264A+1.264

(11)

該擬合的R2=0.919 9,擬合效果較好。

3 MTOAC萃取鈾的分配比模型的驗證

總結對f(cC0,cU)、f1(cR0)和f2(A)3個函數的擬合結果,可以得到MTOAC萃取鈾的分配比D的數學模型為:

f1(cC0,cU0)·f2(cR0)·f3(A)=D

(12)

其中:

與實驗室數據對比,計算每個實驗數據與計算值的偏差,實驗數據均基于水相碳酸鹽濃度(0.02～1.2 mol/L)、水相鈾濃度(0.02～0.17 mol/L)、萃取劑濃度(0.05～0.3 mol/L)和相比(0.2～5)共4個因素,計算公式為:

(13)

式中:Dexp為萃取分配比的實驗值;Dcal為利用MTOAC萃取鈾的分配比模型計算得出的分配比。偏差計數如圖7所示。

圖7 偏差百分比統計Fig.7 Statistical chart of percentage deviation

可以看出,該模型與實驗值擬合效果較好,絕大部分數據的偏差都在±10%以內,基本呈正態分布。但仍有個別數據偏差較大,cUR>0.5cR0時偏差超過±15%以上的數據均為平衡時有機相鈾濃度較高時的數據。

4 結論

1)本文建立的碳酸鹽體系下MTOAC萃取鈾的分配比模型在一定范圍內擬合效果較好,并且可以與萃取機理相符合。通過該模型,可以根據萃取時可測量的初始條件快速預估出MTOAC萃取鈾的分配比,能夠給萃取器的仿真模擬提供幫助,促進了堿性乏燃料后處理的工業化發展。

2)相較于其他萃取體系,MTOAC萃取鈾的分配比數據相對較少,模型的總數據量不足,模型可能不夠精確,需要更多的實驗數據來修正函數中的各個參數。