“瞬時速度”的兩種教學(xué)序列探討
——基于學(xué)習(xí)心理學(xué)角度

丁潤康，陳 剛

華東師范大學(xué)教師教育學(xué)院，上海 200062

人教版高中《物理》必修一“位置變化快慢的描述——速度”一節(jié)在瞬時速度概念的獲得過程中，有一句話“當Δt 非常非常小時，運動快慢的差異可以忽略不計，此時，我們就把叫作物體在時刻t 的瞬時速度”［1］。對于教材中的這句話，學(xué)生可能會產(chǎn)生疑問——多大的Δt 才是非常非常小的？瞬時速度概念實際上是位置關(guān)于時間函數(shù)的導(dǎo)數(shù)，但是初升高一的學(xué)生并沒有對導(dǎo)數(shù)進行系統(tǒng)的學(xué)習(xí)，作為替代需要使用極限推理的方法引導(dǎo)學(xué)生獲得相應(yīng)結(jié)論。

對于瞬時速度概念的獲得，通常存在兩種教學(xué)序列，一個是從位置－時間函數(shù)入手，另一個則是從位置－時間圖像入手，兩種序列均是合乎邏輯的，同時二者又具備著各自的優(yōu)勢以及不足之處。本文將從學(xué)習(xí)心理學(xué)的角度出發(fā)，通過教學(xué)任務(wù)分析的手段，分析兩種教學(xué)序列各自的主要結(jié)論以及結(jié)論獲得經(jīng)過的邏輯過程，基于此分析兩種序列的優(yōu)勢以及不足，并從易于學(xué)生理解的出發(fā)點給出一種結(jié)合兩種序列的教學(xué)方案。

1 基于學(xué)習(xí)心理學(xué)的物理概念與規(guī)律的信息加工機制

學(xué)習(xí)心理學(xué)通過研究人類的學(xué)習(xí)機制提出，學(xué)生的學(xué)習(xí)過程是其內(nèi)部對信息進行加工的過程，并遵循相應(yīng)的信息加工機制，符合學(xué)生學(xué)習(xí)機制的教學(xué)才是真正有效的教學(xué)［2］。

1.1 物理概念與規(guī)律的結(jié)論獲得的邏輯機制

學(xué)生在學(xué)習(xí)物理概念或規(guī)律時，總是通過實驗歸納或者理論分析的途徑，并經(jīng)歷一系列邏輯的信息加工過程獲得結(jié)論。符合邏輯的信息加工方式包括穆勒五法（求同法、差異法、共變法、求同求異法和剩余法）以及演繹推理，學(xué)生通過以上的信息加工過程可以建立物理量之間的因果聯(lián)系，并由此完成對物理概念與規(guī)律的學(xué)習(xí)［3］。

瞬時速度教學(xué)的主要結(jié)論分別是通過共變法、演繹推理以及極限推理的信息加工方式獲得的。

共變法的運用同樣需要提供若干個場合，這些場合中只有一個先行條件發(fā)生變化，被研究的現(xiàn)象同樣發(fā)生變化，如此便可以推斷該先行條件與被研究的現(xiàn)象之間存在因果聯(lián)系，其結(jié)構(gòu)如表1 所示。

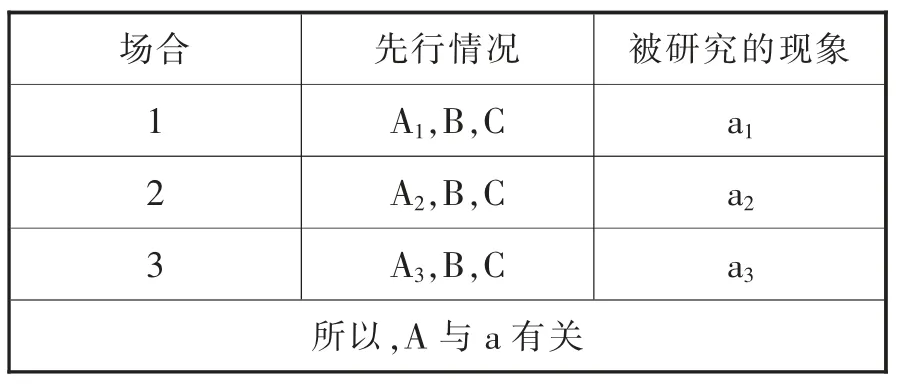
表1 共變法的結(jié)構(gòu)

演繹推理策略是通過已知的具備一般性的前提得出有關(guān)特殊性知識的結(jié)論的一種推理方式，其最基本的形式是三段論，由大前提、小前提以及結(jié)論三個命題構(gòu)成，其結(jié)構(gòu)如表2 所示。

表2 三段論演繹推理的結(jié)構(gòu)

極限推理的運用需要已知物理量隨著一個先行條件的連續(xù)單調(diào)變化而同時出現(xiàn)連續(xù)單調(diào)變化，假設(shè)該條件連續(xù)單調(diào)變化直至達到一個理想的極限狀態(tài)，這個極限狀態(tài)往往在現(xiàn)實中難以或者無法實現(xiàn)，可以推測被研究的物理量同樣隨之發(fā)生連續(xù)單調(diào)變化并達到對應(yīng)的一種極限狀態(tài)［4］。

1.2 教學(xué)任務(wù)分析

教學(xué)任務(wù)分析，可以將一個較為復(fù)雜結(jié)論的獲得，分解成一系列子結(jié)論的獲得，并且梳理完成獲得各子結(jié)論的序列以及學(xué)習(xí)者的必備技能。其重點在于確定教學(xué)活動需要獲得的結(jié)論，以及對應(yīng)的一系列子結(jié)論，同時需要對子結(jié)論獲得所經(jīng)歷的邏輯過程進行分析，并據(jù)此給出學(xué)習(xí)者參與教學(xué)活動的必備技能。根據(jù)教學(xué)任務(wù)分析，教師可以篩選出服務(wù)于結(jié)論獲得的信息并進行合理有序的呈現(xiàn)，引導(dǎo)學(xué)生通過邏輯過程最終習(xí)得對應(yīng)的學(xué)習(xí)結(jié)果。

2 “瞬時速度”兩種教學(xué)序列的教學(xué)任務(wù)分析

2.1 瞬時速度教學(xué)需要獲得的主要結(jié)論

從位置-時間函數(shù)入手的子結(jié)論：

從位置-時間圖像入手的子結(jié)論：

子結(jié)論b-1：x-t 圖像上A，B 兩點間平均速度的大小可以用割線AB 的斜率表示。

子結(jié)論b-2：當B 點逐漸靠近A 點時，割線AB 也逐漸向A 點切線靠近。

子結(jié)論b-3：當A，B 兩點重合時，割線AB也與A 點切線重合。

子結(jié)論b-4：當Δt 趨近于0 時，x-t 圖像上A，B兩點間的平均速度的大小可以用過A 點的切線斜率表示為一個定值。

2.2 結(jié)論建立的邏輯過程

2．2．1 從位置－時間函數(shù)入手的教學(xué)序列

教師可以隨意列出一個表示物體位置x 與時刻t 關(guān)系的運動函數(shù)，如x（t）=t2-3t+7。取由時刻t 到時刻t+Δt 內(nèi)的一段時間，則物體對應(yīng)的位移Δx 可以用x（t+Δt）-x（t）得到。隨意取一個時刻t=1 s，分別在Δt=1 s，0.5 s，0.1 s，0.01 s，0.001 s的條件下計算出位移Δx 以及平均速度的值。

表3 運用共變法獲得子結(jié)論a-1

遵循極限推理的邏輯方法，對子結(jié)論a-1進行極限處理，可以得到子結(jié)論a-2：當Δt 趨近于0 時，即t+Δt 十分接近t 時，平均速度的值等于一個定值。

2．2．2 從位置－時間圖像入手的教學(xué)序列

教師在位置－時間圖像上隨意繪制一條曲線，并在其上任意取A，B 兩點，如圖1 所示。讓學(xué)生找出x-t 圖像中蘊含的A，B 兩點之間的時間ΔtAB以及位移ΔxAB的信息，并借此進一步找到A，B 兩點之間的平均速度在x-t 圖像上的表示方式。

圖1 位置－時間圖像（x-t 圖像）

遵循三段論的演繹推理的邏輯過程，得出子結(jié)論b－1：x-t 圖像上A，B 兩點間的平均速度的大小可以用割線AB 的斜率表示。

表4 運用演繹推理獲得結(jié)論

第二步，將“平面直角坐標系中直線斜率為縱坐標的變化量與橫坐標的變化量的比值”作為大前提，得到“割線AB 的斜率為，即”。

第三步，將“平均速度vAB的大小與割線AB的斜率大小相等”作為大前提，得到子結(jié)論b－1：x-t 圖像上A，B 兩點間的平均速度的大小可以用割線AB 的斜率大小表示。

將B 點逐漸向A 點靠近來縮小兩點的時間間隔Δt，如圖2 所示，并引導(dǎo)學(xué)生識別割線AB隨之發(fā)生的變化。遵循共變的歸納方法，獲得子結(jié)論b－2，其邏輯過程如表5 所示。

圖2 x-t 圖像（取曲線上B1，B2，B3 三點）

表5 運用共變法獲得子結(jié)論b－2

遵循極限推理的邏輯方法，對子結(jié)論b－2 進行極限處理，當B 點與A 點非常靠近，直至重合時，獲得子結(jié)論b－3：當A，B 兩點重合時，割線AB 也與A 點切線重合。

遵循三段論的演繹推理的邏輯過程，將此前獲得的子結(jié)論b－1 和b－3 作為大前提，可以得出子結(jié)論b－4：當Δt 趨近于0 時，x-t 圖像上A，B兩點間的平均速度的大小可以用過A 點的切線斜率的大小表示為一個定值。

2.3 兩種教學(xué)序列的分析

通過教學(xué)任務(wù)分析，兩種教學(xué)序列均能夠通過符合邏輯的方式引導(dǎo)學(xué)生獲得結(jié)論，但是二者在具體的結(jié)論建立過程中，對學(xué)生提出的要求有所不同。

從位置-時間函數(shù)入手的教學(xué)序列，對于學(xué)生而言不具有學(xué)習(xí)難點。學(xué)生易于通過具體的數(shù)值獲得隨Δt 變化，并據(jù)此進行極限推理。當Δt 不斷減小，趨近于0 時平均速度的值等于一個定值，從而習(xí)得瞬時速度的概念。其結(jié)論獲得的邏輯過程中選取的函數(shù)，雖然是隨意選取的，但由于子結(jié)論是針對選取的函數(shù)通過相應(yīng)的邏輯過程獲得的，與具體的數(shù)值存在比較強的關(guān)聯(lián)，而對于其他運動狀態(tài)物體的位置-時間函數(shù)是否成立未知，需要通過類似的邏輯過程進行證明，普遍性稍弱。該教學(xué)序列適合學(xué)習(xí)基礎(chǔ)稍弱的學(xué)生。

從位置-時間圖像入手的教學(xué)序列，學(xué)生首先需要將平均速度轉(zhuǎn)化為x-t 圖像上的割線斜率，通過共變法以及極限推理得到子結(jié)論后，還需要經(jīng)過將割線斜率返回到平均速度的過程。相比于從位置-時間函數(shù)入手的教學(xué)序列，學(xué)生需要額外具備與位置-時間圖像相關(guān)的識圖能力，同時增加了速度與割線斜率進行轉(zhuǎn)化的過程，教學(xué)過程更加復(fù)雜繁瑣，而且給學(xué)生帶來的思維負擔(dān)也更重。但是，由于位置-時間圖像屬于隨意繪制的一條曲線，同時圖像上的各點同樣是隨意選取的，具備相對較強的普遍性。該教學(xué)序列適合學(xué)習(xí)基礎(chǔ)較強的學(xué)生。

3 結(jié)合兩種序列的教學(xué)詳案

從學(xué)生易于理解的角度來看，位置-時間圖像的部分內(nèi)容適合置于瞬時速度的概念學(xué)習(xí)之后，作為平均速度以及瞬時速度在圖像上的表示這一部分內(nèi)容供學(xué)生學(xué)習(xí)，學(xué)生在理解瞬時速度的概念之后，更加容易理解瞬時速度以x-t 圖像上對應(yīng)點的切線斜率表示。

本文接下來將選取位置-時間函數(shù)作為出發(fā)點，在學(xué)生習(xí)得瞬時速度概念之后，通過與從位置-時間圖像入手的教學(xué)序列類似的邏輯過程，引導(dǎo)學(xué)生習(xí)得瞬時速度在位置-時間圖像中的表示方式，并以教學(xué)問題鏈的形式提供一種啟發(fā)式教學(xué)的詳案。

3.1 瞬時速度的概念（從位置－時間函數(shù)入手）

生：可以采用物體在某一時刻附近的很小一段時間內(nèi)的平均速度來近似表示物體在該時刻的速度。

師：我們來分析一下同學(xué)們的想法是否可行。要求平均速度需要知道哪些物理量？

生：物體運動的一段時間Δt 以及這段時間內(nèi)的位移Δx。

師：我們隨意取一個物體的運動過程，其位置x 與時間t 存在關(guān)系：x（t）=t2-3t+7。取由t 到t+Δt 的一個時間段，這個時間段內(nèi)物體的位移如何表示？

生：末位置坐標值減去初位置坐標值，即Δx=x（t+Δt）-x（t）。

師：該時間段內(nèi)的平均速度怎么表示？

師：現(xiàn)在我們要將時間段縮短并接近時刻t，那么Δt 應(yīng)怎樣？

生：非常小。

師：怎么做到非常小呢？隨意取某一個時刻，比如在時刻t=1 s 時，我們先分別取Δt=1 s，0.5 s，0.1 s，0.01 s，0.001 s，不斷將Δt 變小，觀察這段時間內(nèi)的平均速度的值是怎樣變化的（表6）。

表6 位置－時間函數(shù)的各數(shù)據(jù)隨Δt 的變化

生：隨著Δt 的變小，平均速度在不斷接近一個定值（子結(jié)論a-1）。

師：按照同學(xué)們的想法，我們讓Δt 不斷減小，使得Δt 無限小，甚至等于0，同學(xué)們認為此時的平均速度會怎么樣？

生：平均速度會等于那一個定值（子結(jié)論a-2）。

師:經(jīng)過分析，當Δt 無限小，趨近于0 時，即t+Δt 十分接近t，平均速度會成為一個定值，可以把此時的平均速度稱為物體在時刻t 的瞬時速度，大小就等于這一個定值。

3.2 瞬時速度在位置－時間圖像上的表示方式

師：一個物體的位置與時間的關(guān)系，除了位置－時間函數(shù)以外，還能以位置－時間圖像的形式表示出來。物體位置變化的快慢可不可以在x-t圖像上表示出來？

生：相同的橫坐標變化，即相同的時間間隔內(nèi)，位置變化越大，表現(xiàn)為縱坐標變化大。物體位置變化快，則整體圖像會“陡”一些。

師：x-t 圖像能夠表現(xiàn)物體位置變化的快慢，那么也就是說，它能夠體現(xiàn)出物體的速度，具體是如何表示的？ 比如說這里有一個x-t 圖像（如圖1），這條曲線上面任取A，B 兩點，如何表示兩點之間的平均速度？ 根據(jù)平均速度的定義來思考。

師：因為A，B 兩點是任取的，所以可以證明x-t 圖像上任意兩點之間的平均速度可以用經(jīng)過兩點的割線的斜率表示。那么，瞬時速度又是如何表示的呢？ 首先回想一下，我們是如何獲得瞬時速度的概念的？

生：平均速度隨著Δt 的減小而不斷接近一個定值，在極限情況下，當Δt 趨近于0 時，平均速度就等于那個定值，此時的就是物體在時刻t 的瞬時速度。

師：我們要求瞬時速度在x-t 圖像的表示方式，同樣可以遵循這一套步驟。第一步需要做什么？

生：減小Δt 的值。

師：我們可以將B 點逐漸向A 點靠近，依次取B1，B2，B3三個點（如圖2），滿足Δt 逐漸減小。接下來做什么？

生：觀察平均速度即割線斜率隨Δt 的變化。

師：發(fā)現(xiàn)隨著Δt 的變小，割線逐漸向A 點的切線靠近（子結(jié)論b－2）。接下來——

生：取極限情況，當Δt 趨近于0 時，割線就成為A 點的切線（子結(jié)論b－3）。

師：此時平均速度就是物體在A 點對應(yīng)時刻的瞬時速度vA。那么，A 點的瞬時速度在x-t圖像中如何表示？

生：A 點的瞬時速度就是x-t 圖像上該點的切線斜率（子結(jié)論b－4）。

師：因為A，B 兩點是隨意選取的，所以x-t圖像上的任意一點的瞬時速度可以用該點的切線方向表示。

4 總 結(jié)

對于瞬時速度概念獲得的兩種教學(xué)序列，從學(xué)習(xí)心理學(xué)角度運用教學(xué)任務(wù)分析的手段，對各自需要獲得的主要結(jié)論及其邏輯過程進行分析，得到了以下結(jié)論：從位置－時間函數(shù)入手進行教學(xué)，學(xué)生相對易于理解，但是由于獲得結(jié)論的過程只對選取的函數(shù)有效，降低了結(jié)論的普遍性；而從位置－時間圖像入手進行教學(xué)，其主要結(jié)論的獲得過程適用于位置－時間坐標系上的任意一條曲線，普遍性相對更高，但是需要學(xué)生對速度與圖像上對應(yīng)的割線或切線的斜率進行轉(zhuǎn)換，在一定程度上又增加了學(xué)生的理解難度。

為便于學(xué)生理解，對于“位置變化的快慢——速度”一節(jié)“瞬時速度”部分的教學(xué)可以選擇從位置－時間函數(shù)入手，經(jīng)歷對應(yīng)的邏輯過程習(xí)得瞬時速度的概念以及在位置－時間圖像中的表達方式，從符合學(xué)生學(xué)習(xí)機制的角度進行教學(xué)。