錨桿與錨索協同錨固的能量分析研究

張新過，黨鵬遠，朱初初

（1.河南能源化工集團永煤公司 城郊煤礦，河南 商丘 476600；2.中國礦業大學 力學與土木工程學院，江蘇 徐州 221008）

0 引言

我國巷道支護技術經歷了棚式支護到組合支護的發展，在地質力學測試技術、支護材料和支護理論方面等都得到較大程度的發展[1]。而對錨桿、錨索作用原理的認識，從懸吊理論到成梁或成拱理論，發展到改善錨固區圍巖力學性能與應力狀態，特別是圍巖屈服后的力學性能[2]，經歷了長足的發展，有效地提高的錨固體的可靠性[3]。而錨桿支護技術也已經得到廣泛的應用與拓展，并在此基礎上發展了多種針對特定地質狀況的支護技術，錨桿也獲得了從單一桿體到多種形式錨桿的轉變[4]。20 世紀60 年代我國開始應用預應力錨固技術，預應力的應用使得錨桿支護由被動轉變為主動，從而使得預應力錨桿支護技術獲得了大面積的推廣應用[5]。隨后，預應力錨索的出現以及組合錨索支護技術的應用解決了許多復雜地質條件下的巷道支護難題[6-7]。近年來，協同學被應用于錨固支護理論中，并提出一種新的支護設計方法—協同錨固技術[8-13]。協同錨固是指通過調整各個支護參數，協調匹配各種支護構件，使得支護體之間以及支護體與圍巖之間協同工作，達到“1+1≥2”的協同錨固作用。本文從能量角度分析錨桿和錨索支護作用下錨固體和圍巖內能量的轉移和轉化特征，試圖揭示二者之間以及與錨固體、圍巖之間的協同效應，為錨桿和錨索的支護設計提供理論指導。

1 圍巖內的彈性應變能和塑性破壞能

巖石的受載變形和破壞過程是能量不斷轉移和轉化的過程。對于地下工程而言，開挖過程破壞了原有的能量平衡，能量在巷道圍巖內轉移、轉化以達到新的平衡狀態，支護體會影響這一能量過程。

巷道圍巖內的彈性應變能是一個標量，它是某一范圍內圍巖體能量大小的量度，是彈性應變能密度的函數。彈性應變能密度是應變的函數vε=∫σidεi，而彈性應變余能密度是應力的函數vc=∫εidσi，對于彈性能量而言，二者相等，可根據物理方程即胡克定律將二者相互轉化。因此，彈性應變能密度的計算采用彈性應變余能密度計算式vε=∫εidσi將物理方程代入可得：

因此，要計算巷道圍巖內的彈性能就需要圍巖應力分布式。

1.1 圍巖應力及變形

設有一圓形巷道，半徑為a，原巖應力為p0，開挖后圍巖分區采用傳統的三區劃分，即由破碎區、塑性區和彈性區三個部分組成，考慮均勻、各向同性、平面應變情形，圍巖塑性破壞準則取Mohr-Coulomb 屈服準則，即：

下標“p”和分“c”別表示塑性區和破碎區，彈性區以下標“e”表示。根據Mohr-Coulomb 屈服準則可求得各區應力和位移分布式[18]。

式 中：Ac=(pi+Bc)/aNc-1；Bc=cccotφc；Ap=2(p0+Bp)/（Np+1）RpNp-1；Bp=cpcotφp；σrp=(2p0-Sp)/（Np+1）；pi為支護力；c 為粘聚力；φ為內摩擦角；Rp為塑性區半徑。

式中：α=(1+sinφ)/(1-sinφ)，φ為破裂角；h=(1-μ)(Nα+1)/(N+α)-μ；i=B+p0。

1.2 巷道圍巖內的彈性能密度和塑性能密度

將各區應力分布式代入彈性應變能密度計算式（1），可求得各區彈性應變能密度的分布式。

彈性區：

破碎區和塑性區的巖體總能量是指巷道開挖后能量重分布以后的彈性應變能和巖體用于塑性破壞的塑性應變能之和，根據能量守恒定律，總能量等于外力所做的功與原巖應變能之和：Q=Qe+Qp=W+Q0，其中Q0為原巖應變能，W 為巷道開挖后外力對巖體所做的功。

取巷道圍巖部分巖體考慮，外邊界受力為σr，位移為ur，巷道開挖后巖體內的總能量為原巖應變能與外力對其所做的功之和，若巖體始終處于彈性狀態則能量以彈性能儲存在巖體中，若巖體發生塑性破壞則部分能量轉化為塑性能。根據各區應力和位移分布式可求出外力功：

彈性區巖體沒有塑性破壞，總能量完全儲存在彈性能中，總能密度即為彈性能密度。而巖體內的塑性能密度即為總能量密度與彈性能密度的差值νp=v (r)-vε。

取巷道半徑a=3 m，彈性模量E=20.4 GPa，泊松比μ=0.3，粘聚力cp=5.31 MPa，cc=2.0 MPa，內摩擦角φp=38°，φc=15°，原巖應力p0=20 MPa。利用MATLAB 軟件可得到彈性能密度和總能量密度在圍巖內的分布曲線，如圖1 所示。

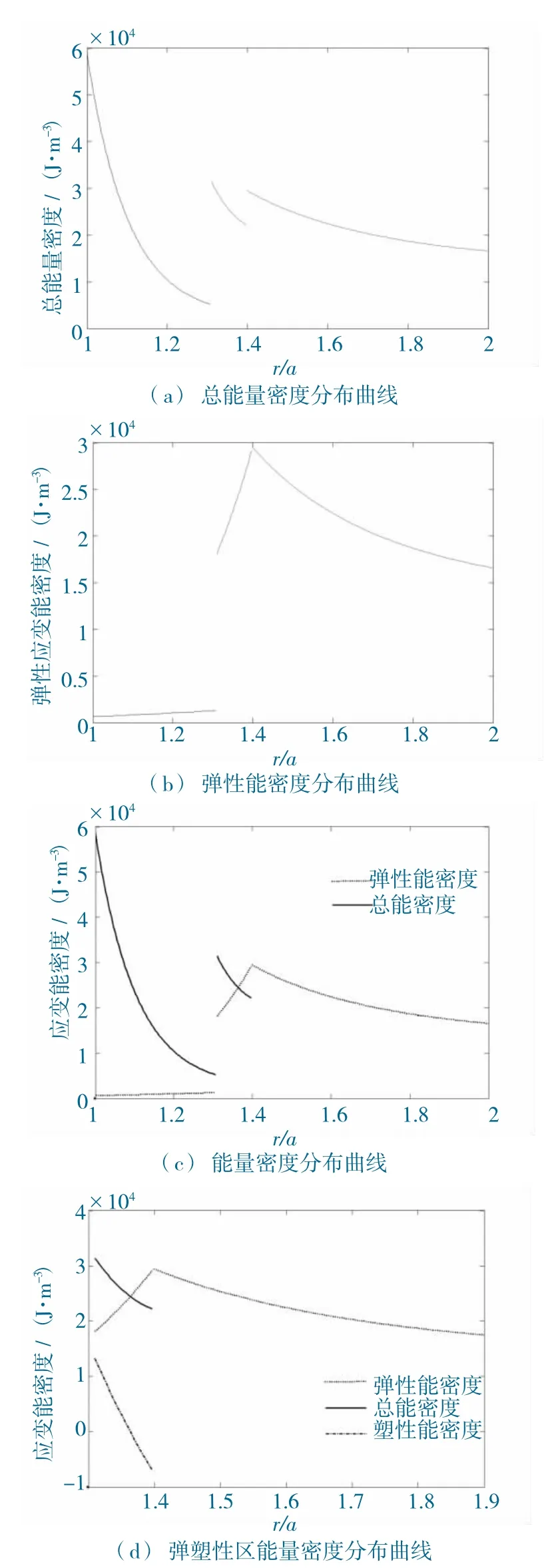
圖1 能量密度分布曲線Fig.1 Curve of energy density distribution

由圖1 可知，巷道開挖后圍巖內的總能量在巷道附近集聚，使得巷道周邊圍巖產生塑性變形和破壞，然后往深部巖體轉移，總能量迅速減少。

根據對塑性區和破裂區圍巖能量的計算分析，發現在塑性區部分范圍內巖體的彈性應變能超過了總能量，在實際情況中這是不可能的。分析外力功的計算式可知，在緊鄰彈性區的部分塑性區范圍內巖體的位移發展過快，使得W(R+dr)-W（r）＜Qep（r+dr）-Qep（r），這是違背能量守恒定律的。因此，由塑性位勢理論求出的位移不適用于塑性區。

1.3 總能量密度計算式的修正

現對模型做如下修改：將破碎區巖體與周圍巖體分離開，代之以均布內壓，并單獨分析破碎區巖體，如圖2 所示。

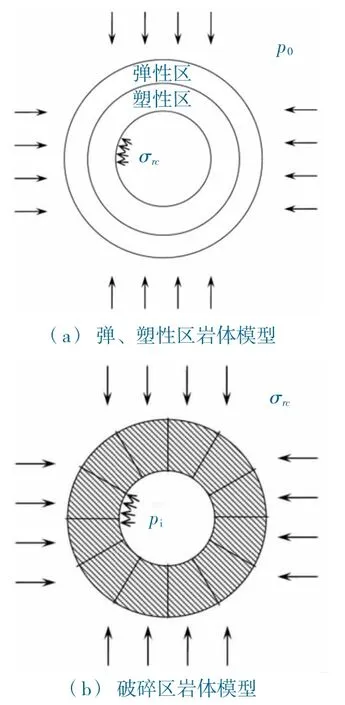
圖2 巷道圍巖分離模型Fig.2 Separation model of roadway surrounding rock

對于存在內壓的巷道圍巖彈塑性分析是一個經典問題，在求解圍巖的位移時假設巖體為理想彈塑性體，即塑性區體積不可壓縮，可得塑性區位移：

那么，塑性區巖體內的總能量密度為：

分布在破碎區和塑性區的總能量為：

塑性區內的總能量為：

破碎區內的總能量為：

破碎區巖體內的總能量密度計算式仍取式（11）第二式。此時，圍巖彈性能密度和總能量密度分布曲線如圖3 所示。

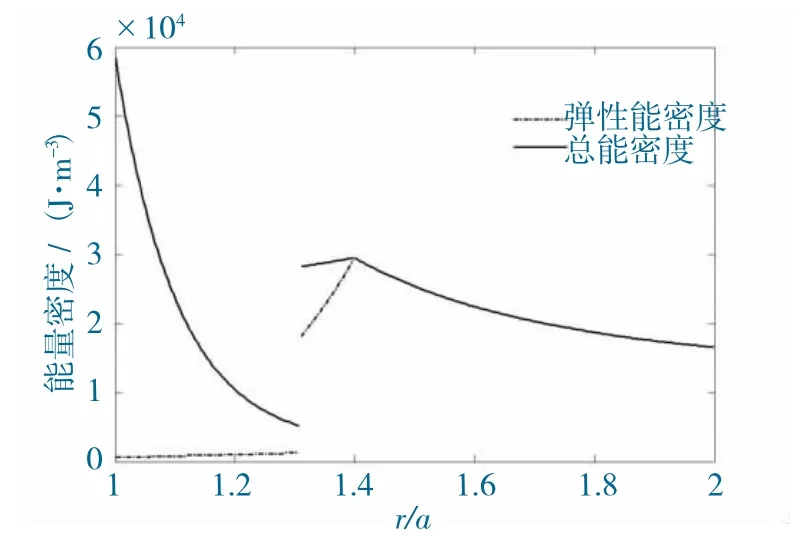
圖3 圍巖能量密度曲線Fig.3 Energy density curve of surrounding rock

由圖3 可知，能量在巷道附近圍巖內大量集聚；破碎區的位移除了塑性位移以外還存在因巖石破裂膨脹產生的位移，根據式（10）可知，內部巖體位移越大外部巖體對內部巖體做功越多，能量在圍巖內的集聚程度越大。但破碎區巖體內的總能量是一定的，如式（16），內部巖體能量集聚必然引起外部巖體能量的減少。

2 錨桿錨索協同工作時圍巖能量分析

2.1 錨桿作用機理分析

錨桿的主要作用對象是強度和承載能力較低的巖體，對于巷道圍巖深部塑性區和彈性區的巖體，錨桿所發揮的作用與破碎區相比較小。錨桿的主要作用是改善發生塑性變形和破碎的巖體的力學性質，不同程度地提高巖體強度，改變巖體的變形特性。對于巷道圍巖深部強度較高的塑性區和彈性區巖石，錨桿對巖石強度和變形的影響不大；對于破碎區強度較低的巖石，錨桿對其強度有比較明顯的影響。對圍巖受拉、受剪區域，錨桿可以改善巖體的應力狀態；對節理、裂隙等不連續面，錨桿可以提高結構面的抗剪強度，阻止結構面的張開和滑動；對于較破碎的巖體，錨桿可抑制巖體的擴容變形，明顯提高錨固區巖體的整體強度和完整性[2]。

現假設錨桿的主要作用是提高破碎區巖體的力學參數，即通過提高粘聚力和內摩擦角提高錨固范圍內巖體的強度，通過提高彈性模量減小錨固體的變形。

2.2 錨索作用機理分析

錨索的作用主要是將錨桿支護形成的次生承載層與圍巖的關鍵承載層相連，充分調動深部圍巖的承載能力，使更大范圍內的巖體共同承載，提高支護系統的整體穩定性[15]。對于巷道附近巖體而言，錨索的作用可以看作是對巷道圍巖表面施加支護力pi，改善錨索作用范圍內圍巖的應力狀態。相對于單體錨索，組合錨索作用范圍較大，對于錨桿錨固巖體支護優勢明顯。因此，將錨索的支護作用看作是對錨桿錨固體施加均布支護力。

2.3 錨桿錨索協同工作時圍巖能量變化特性

現仍以上相同的粘聚力、內摩擦角和支護力，分析錨桿、錨索對破碎區圍巖能量的影響。各曲線圖如圖4 所示。

由圖4 可見，隨著內摩擦角的增大，巖體中的總能量和塑性能將趨于定值。而在實際工程中，圍巖的內摩擦角一般大于15°，因此試圖采用支護手段提高錨固體的內摩擦角對提高巷道穩定性的意義不大。

粘聚力由1.0 MPa 增加到2.0 MPa 時總能量和塑性能均減少73%，由2.0 MPa 增加到3.0 MPa 時總能量和塑性能均減少59%；由于注漿可以顯著提高錨固體的粘聚力，因此采用注漿手段加固破碎區圍巖可在一定程度上抑制圍巖的繼續破壞。

支護力由0 增加到0.8 MPa 時總能量和塑性能均減少65%；而在現有支護條件下，對巷道提供0.8 MPa 的均布支護力是不現實的，因此，提高支護強度可增加巷道的穩定性，但并不能阻止圍巖的破壞，對圍巖破裂區的大小影響甚微。

彈性模量由10.0 GPa 增加到20.0 GPa 時總能量和塑性能均減少50%，由30.0 GPa 增加到40.0 GPa 時總能量和塑性能均減少26%。而提高錨固體的彈性模量，需要極高的錨桿支護密度，工程實踐中不具備操作性。

綜上所述，在有效范圍內，與內摩擦角和彈性模量相比，提高錨固體的粘聚力和支護力對破碎區圍巖的總能量影響較明顯。

圖5 和圖6 分別為巷道表面圍巖位移和破碎區圍巖塑性能關于破碎區范圍的曲線圖。

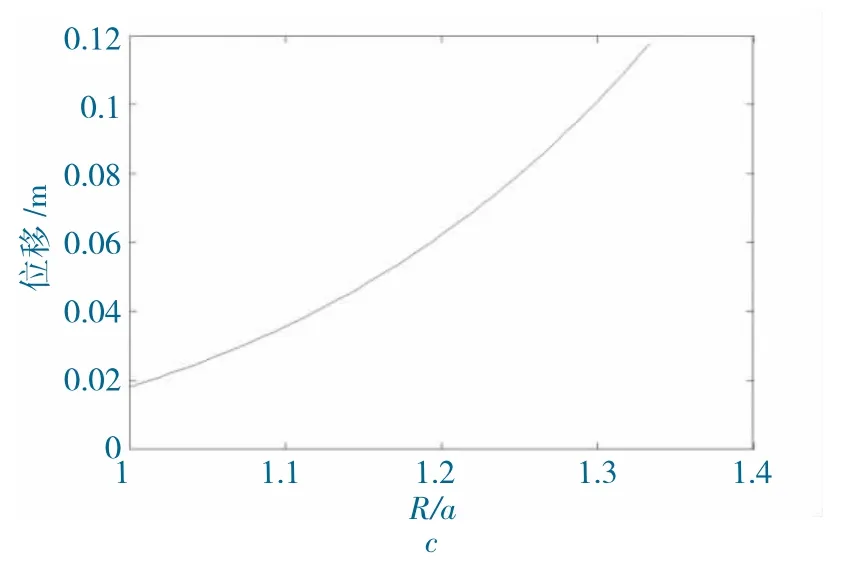
圖5 位移-破碎區范圍關系Fig.5 Relationship between displacement and cracked region radius

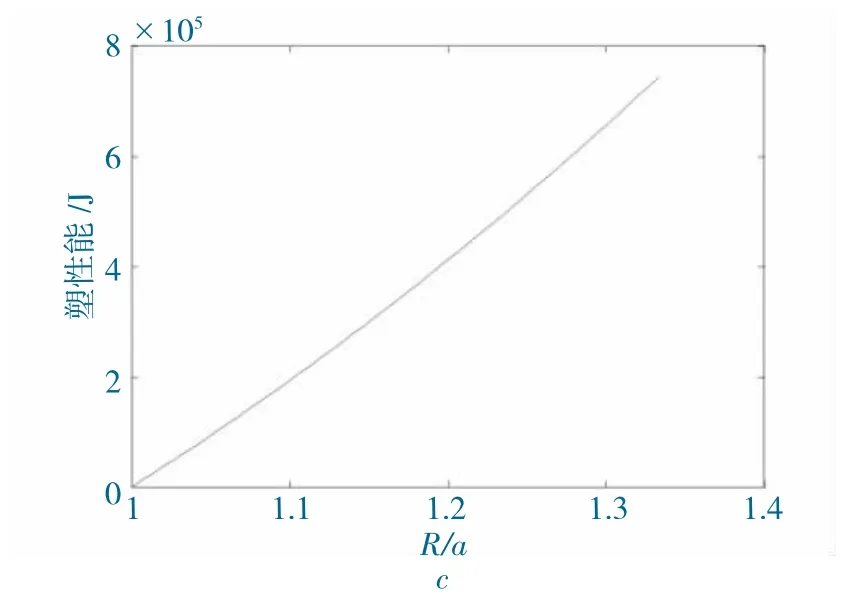
圖6 塑性能-破碎區范圍關系Fig.6 Relationship between plastic energy and broken zone range

圍巖位移和塑性破壞能均對破碎區范圍敏感，且根據總能量計算式（10）知，位移的變化直接影響圍巖總能量的大小。而影響破碎區范圍的主要因素是原巖力學參數和原巖應力，破碎區巖體的力學參數和支護力對其影響有限。因此，為分析錨桿與錨索的支護對圍巖能量的影響，需要排除破碎區范圍這一影響因子，從保持破碎區范圍不變和塑性能密度兩個方面著手。

現以破碎區范圍不變為條件分析3 個參數對破碎區圍巖內能量的影響，各曲線圖如圖7 所示。

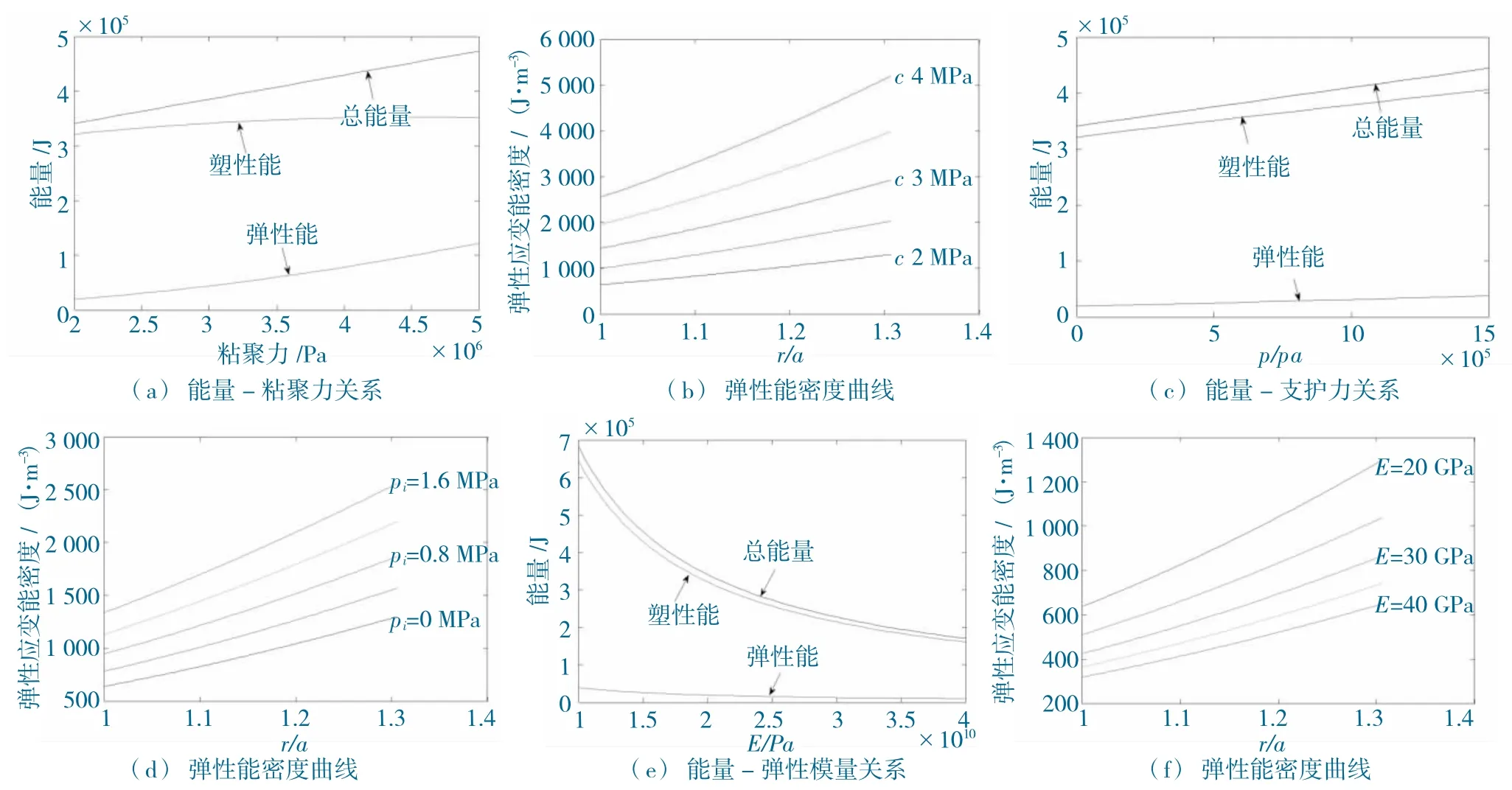
圖7 破碎區圍巖能量變化Fig.7 Energy change of surrounding rock in broken zone

分析各曲線圖可知：粘聚力和支護力的提高均可以增加圍巖內的彈性能；與支護力相比，粘聚力的提高可以較明顯的提高破碎區巖體內的彈性能，但對塑性破壞能影響較小，粘聚力由2.0 MPa 增加到4 MPa，塑性能僅增加9%；彈性模量的增加可以減少圍巖內的能量，但在增加到一定程度后影響減弱，彈性模量由10 GPa 增加到20 GPa，塑性能與彈性能均減少50%，由30 GPa 增加到40 GPa，塑性能與彈性能均減少25%。

圖8 為破碎區巖體的粘聚力、彈性模量和支護力對塑性能密度的影響曲線。由圖可知：粘聚力的提高加劇了塑性能在巷道附近圍巖中的集聚程度；彈性模量的增加可以有效減少破碎區巖體的塑性能和塑性能集聚程度；增加支護力可以減少破碎區巖體的塑性破壞能。

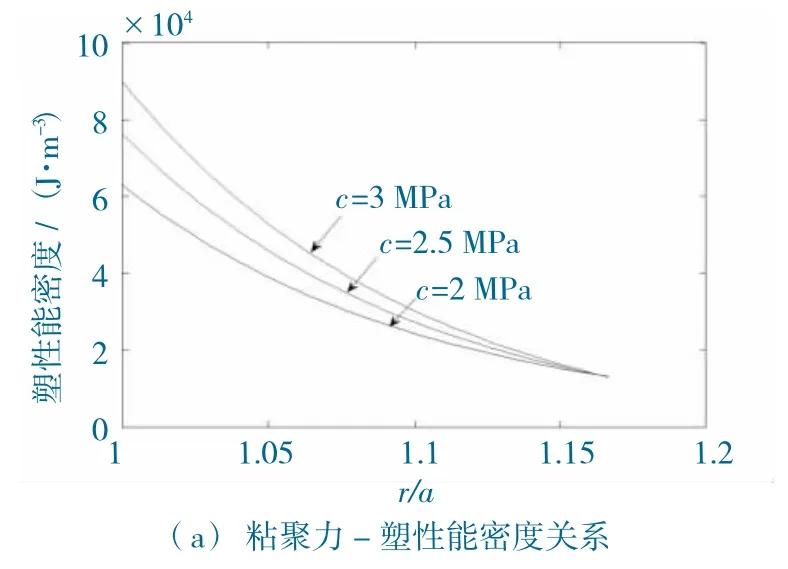
圖8 塑性能密度分布曲線Fig.8 Curve of plastic energy density distribution

綜上所述，提高粘聚力和支護力可以減少破碎區塑性破壞總能量，這是由于破碎區范圍減少的緣故。但是，粘聚力的提高增加了破碎區塑性能集聚程度、增加了破碎區彈性能，支護力的提高減少了塑性能，增加了彈性能。工程實踐中，注漿和錨桿加固提高加固區圍巖粘聚力可在一定程度上減小破碎區范圍抑制圍巖繼續破壞；組合錨索支護可減弱加固區圍巖的塑性破壞程度。

物體的最低能量狀態是最穩定的。若圍巖內儲存的能量較高則較容易失穩，釋放能量，發生巖爆。支護的目的不應該僅僅是控制圍巖的變形，提高圍巖強度，而是在盡可能減少圍巖彈性能量的前提下控制圍巖的變形，提高圍巖的強度。因此，在對巷道支護時需要協調匹配3 參數，在提高錨桿預應力增加錨固區巖體粘聚力減少破碎區范圍的同時，需要施加錨索為圍巖提供均布支護力減少塑性破壞能，使圍巖處于少破碎低能量的穩定狀態。

為保證錨桿與錨索協同工作以維持巷道圍巖的穩定，錨桿的預應力需要與組合錨索的預應力相配合，且錨桿的彈性模量需要與錨桿和錨索的預應力相匹配，在減少破碎區范圍的同時，減弱塑性破壞能集聚程度，降低圍巖彈性能，使圍巖處于少破碎、均勻破碎和低能量的穩定狀態。

3 結論

（1）通過計算分析巷道開挖后圍巖內能量分布特征，發現根據塑性位勢理論得到的位移分布式有誤，由此位移所求塑性區總能量在部分范圍內小于圍巖彈性能，違背能量守恒定律。

（2）在破碎區圍巖的力學參數中，粘聚力相比與內摩擦角對圍巖能量影響較大；支護力的增加可以減少破碎區圍巖的塑性破壞能及其集聚程度，增加圍巖的彈性能，有利于圍巖穩定。

（3）增加錨桿預應力可以增大巖體的粘聚力，粘聚力的增加可以減少破碎區范圍，但會加劇塑性能的集聚，需要配以組合錨索為圍巖提供均布支護力，減弱圍巖塑性能集聚程度。

（4）錨桿的預應力需要與組合錨索的預應力相配合，且錨桿的彈性模量需要與錨桿和錨索的預應力相匹配，在減少破碎區范圍的同時，減弱塑性破壞能集聚程度，降低圍巖彈性能，使圍巖處于少破碎、均勻破碎和低能量的穩定狀態。