多圓盤上的對偶Toeplitz算子
刁思博
(浙江師范大學(xué)數(shù)理信息學(xué)院,浙江金華321000)
多圓盤上的對偶Toeplitz算子
刁思博
(浙江師范大學(xué)數(shù)理信息學(xué)院,浙江金華321000)
在本文中我們研究多圓盤上的對偶Toeplitz算子,著重研究了Sf與其符號f之間的關(guān)系,討論了當(dāng)Sf可逆時(shí)f滿足的條件,從而進(jìn)一步推出了多圓盤Hardy空間中的譜嵌入定理,得到了Sf≥0的充要條件.這些結(jié)論都是和單位球中的結(jié)論類似的.
多圓盤;對偶;Toeplitz算子
Toeplitz算子是現(xiàn)代算子理論中重要的一類,在一般的算子理論方面,它可以作為模型參考,而在算子理論等方面起著紐帶和橋梁的作用.從上世紀(jì)末以來,人們對于對于Toeplitz算子以及Hankel算子的研究有了各種推廣,比如從單位圓盤推廣到單位球,再到多圓盤等.關(guān)于這些可以參考[1,2,3].另一方面是空間測度的推廣,比如從Hardy空間推廣到Bergman空間,人們自然會(huì)想到在這些推廣過程中,經(jīng)典的Tooeplitz算子理論能否成立,有許多工作表明,在推廣的過程中,存在很多的差異,在這個(gè)過程中,我們不僅需要函數(shù)論的知識,也要借助各種代數(shù),拓?fù)涞姆椒?比如代數(shù)拓?fù)? Banach代數(shù)等.
1 基本概念
設(shè)D為單位圓盤,Dn表示多圓盤,Tn為其邊界,多圓盤上的Hardy空間H2(Tn)為Tn上平方可積函數(shù)組成的Hilbert空間,其正交補(bǔ)記為(H2(Tn))⊥.令P代表從L2(Tn)到H2(Tn)的投影, Q代表L2(Tn)到(H2(Tn))⊥上的投影,Q(g)=(I-P)g.對于φ∈L∞(Tn),我們按以下方式定義H2(Tn)上的Toeplitz算子Tφ:
Tφf=P(φf),f∈H2(Tn)
接下來我們就可以定義(H2(Tn))⊥上的對偶Toeplitz算子:
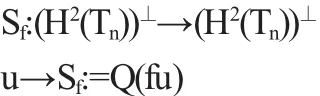
我們知道,投影Q的范數(shù)是1,則對所有的h∈(H2(Tn))⊥,我們有結(jié)論:
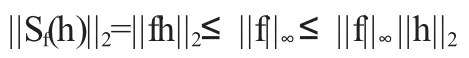
由以上幾種算子的定義,我們可以把H2(Tn)上的乘法算子Mf(f∈L∞(Tn))表示成如下形式:
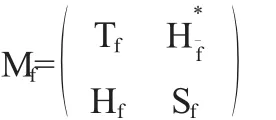
在[8]中研究了單位圓盤和單位球上的對偶Toeplitz算子的一些基本性質(zhì),
2 多圓盤上的對偶Toeplitz算子
引理1對于Tn上的連續(xù)函數(shù)ψ,z∈Tn,有:
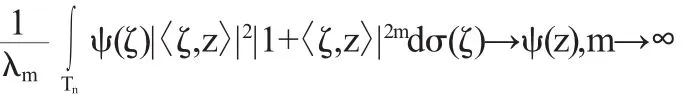
其中,對任意的ε>0,任意固定的z,我們可以構(gòu)造以下鄰域:
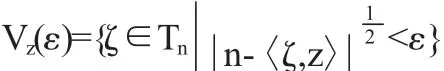
那么在Tn/Vz上我們有
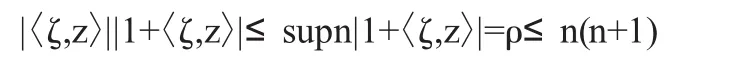
根據(jù)以上式子我們對Tn/Vz上的積分可以進(jìn)行如下計(jì)算:

令一方面,對于0<δ<n(n+1)-ρ<1,經(jīng)過簡單計(jì)算可以得到:
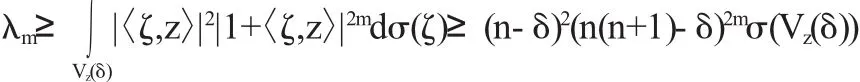
由以上不等式我們可以推出:
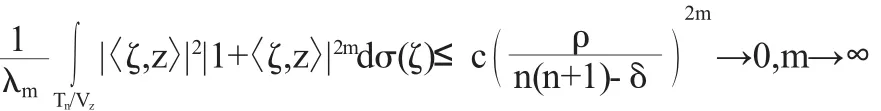
那么現(xiàn)在就有

現(xiàn)在對任意連續(xù)的ψ,有
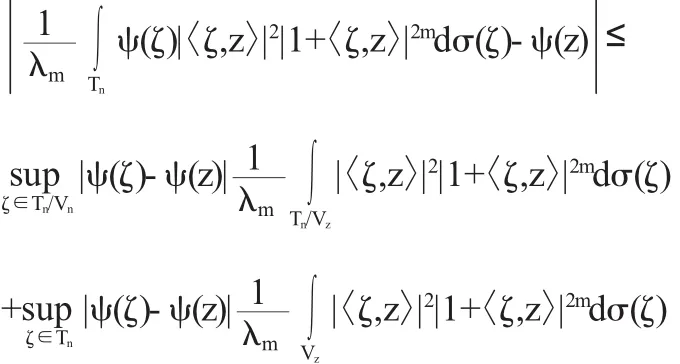
此時(shí)ψ的連續(xù)性保證了我們想要的結(jié)果,引理得證.
定理1設(shè)φ∈L∞(Tn),如果Sφ在(H2(Tn))⊥中可逆,那么符號φ在L∞(Tn)中也是可逆的.
證明這個(gè)定理Bergman空間中是成立的[9],在這里我們根據(jù)引理1采用不同的方法進(jìn)行證明.
如果Sφ是可逆的,那么存在某個(gè)正數(shù)k>0,滿足:||Sφf||2≥k||f||2,對任意的f∈(H2(Tn))⊥都成立.
我們知道投影Sφ的范數(shù)為1,那么我們有:對任意的f∈(H2(Tn))⊥都成立.
此時(shí)我們?nèi)(z)=〈ζ,z〉(1+〈ζ,z〉)m,其中ζ∈Tn,m>1
那么對于任意非負(fù)的連續(xù)ψ,有:
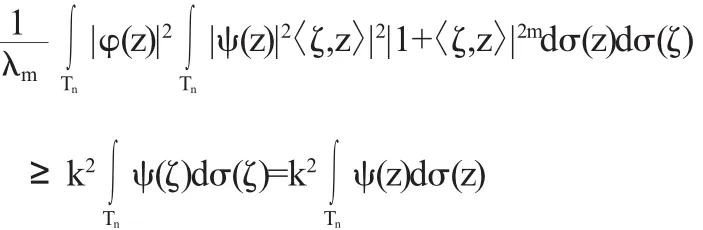
由此,根據(jù)富比尼定理和前面的引理1,我們可以得到
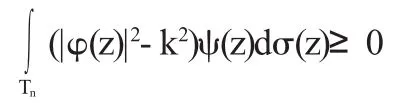
對于Tn中所有連續(xù)非負(fù)的ψ都成立.因此可以得出|φ (z)|≥k在Tn中幾乎處處成立,因此φ在L∞(Tn)中是可逆的.定理得證.
從定理1我們可以得到很多推論,比如多圓盤上對偶Toeplitz算子的譜嵌入定理.在此之前我們先回顧一下本性有界函數(shù)f,記其本性值域?yàn)镽(f),σ(T),r(T)分別表示算子T的譜和譜半徑,那么我們有:
推論1若f∈L∞(Tn),則R(f)=σ(Mf)?σ(Sf).
證明顯然有R(f)=σ(Mf).由于對任意的λ∈C,有Sf-λ= Sf-λ,運(yùn)用定理1就可以得到R(f)?σ(Sf).
[7]我們可以知道對于Hardy空間上的Toeplitz算子,由譜嵌入定理可以立即推出:||Tf||=||f||∞.由此可以得到以下結(jié)果.
推論2定義在L∞(Tn)上的映射η:
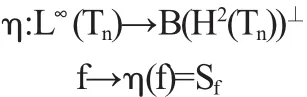
是由L∞(Tn)到B(H2(Tn))⊥的等距映射,即有||Sf||=||f||∞=r(Sf).
證明由推論2和參考文獻(xiàn)中[6]中的命題2.28,我們可以得出:對于f∈L∞(Tn),有
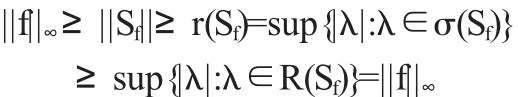
我們可以得到η是等距映射.
接下來我們考慮一類特殊的算子:冪零算子.一個(gè)算子S被稱為冪零算子,若存在某個(gè)正數(shù)n,使得Sn=0,令Sn=0的最小n稱為冪零指數(shù),S被稱為擬冪零算子,于多圓盤上的對偶Torplitz算子,我們有以下結(jié)論:
推論3多圓盤Hardy空間中不存在非零的擬冪零對偶Toeplitz算子.
證明由上文,若Sf是擬冪零算子,則||Sf||=||f||∞=r(Sf)==0,這說明Sf≡0.
更進(jìn)一步的我們可以得到以下推論:
推論4設(shè)f∈L∞(Tn),則Sf≥0當(dāng)且僅當(dāng)f≥0.
證明若f≥0,則〈Sfg,g〉=〈Q(fg),g〉=〈fg,g〉
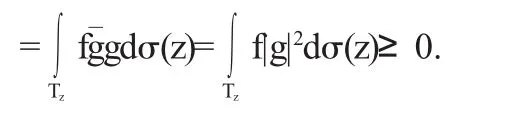
說明Sf≥0.
反過來,若Sf≥0,說明Sf的譜在R+中,由推論1有R(f)?σ(Sf)?R+.即f≥0.
參考文獻(xiàn):
〔1〕DurenP.TheoryofHpspace[M].NewYork:AcademicPress,1970.
〔2〕ZhuK.Operatortheoryinfunctionsspaces[M].New York:MarcelDekker,2000.
〔3〕ConwayJ.Acourseinoperatortheory[M].USA: Amer.Math.Soc.,2000.
〔4〕DurenP.,SchusterA.Bergmanspaces[M].USA:Math. Sur.Mon,2003.
〔5〕McDonald,G.;Sundberg,C,Toeplitzoperatorsonthe disc.IndianaUniv.Math.J.28(1979),no.4,595–611.
〔6〕K.Zhu.Operatortheoryinthefunctionspace[M].Marcel Dekker,Inc.NewYork,1990.
〔7〕W.Rudin.Realandcomplexanalysis[M].McGraw-Hill,NewYork,1974.
〔8〕T.Yu.S.Y.Wu:AlgebraicpropertiesofdualToeplitz operatorsontheorthogonalcomplementoftheDirichletsphere.ActaMath.Sinica(Eng.Ser.)24(11),(2008), 1843-1852.
〔9〕盧玉峰,尚書霞.多圓盤上對偶Toeplitz算子的性質(zhì)[J].數(shù)學(xué)研究與評論,2007(03).
〔10〕于濤,孫善利.加權(quán)Bergman空間上的緊算子.數(shù)學(xué)學(xué)報(bào),2001,vol.44,No.2,233-240.
〔11〕LISong-xiao,HUjun-yun.CompactCperatorson BergmanSpacesoftheUnitBall.[J].ActaMathSinica, 2004,47(5):837-844.
〔12〕RochbergR,WuZ.ToeplitzoperatorsonDirichlet spaces.IntegralEquationandOperatorTheory,1992,15 (2),325-342.
〔13〕WuZhiJian.HankelandToeplitzOperatorson DirichletSpace.IntegralEquationandOperatorTheory,1992,15,no3,503-525.
〔14〕CaoGuangFu,ZhuLu.TheCompactnessofToeplitz OperatorsonDirichletSpaces.ActaMath.Sinica(Chin. Ser),44,(2001),no.2,241-248.
〔15〕LuY,SunS.ToeplitzOperatorontheDirichletSpace [J].ActaMath.Sinica,EnglishSeries,2001,17:643-648.
〔16〕J.Conway.Acourceinfunctionalanalysis[M]. Springer.NewYork,1985.
〔17〕R.Douglas.Banachalgebratechniquesinoperatortheory[M].AcademicPress,NewYork,1972.
〔18〕A.Brown,P.Halmos.AlgebraicpropertiesofToeplitz operators[J].ReineAngew.Math.213(1964):,89-102.
〔19〕BrownA,HalmosPR,AlgebraicpropertiesofToeplitz Operators.J,ReineAngew.Math,1963/1964,213:89-102.
〔20〕DechaoZheng.HankelOperatorsandToeplitzOperatorsontheBergmanSspace,[J].Func.Anal.83(1989),98-120.
O174.56
A
1673-260X(2013)06-0004-02

