如何利用分割法、拼補法求組合圖形的面積

董周濤

計算組合圖形的面積是在學生掌握了平行四邊形、三角形、梯形等基本圖形的面積計算公式后的綜合應用。如何利用分割法、拼補法求組合圖形的面積，幫助學生感悟轉化思想、發展空間觀念呢？可以設計如下教學過程。

一、操作感知，分類提煉

1.自主探究

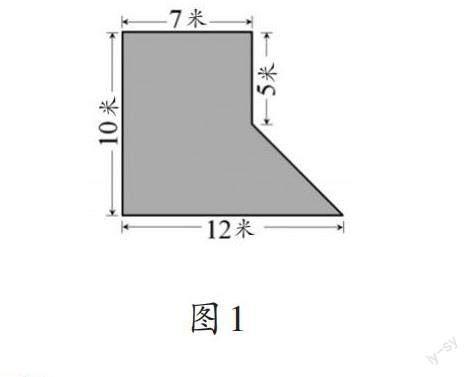
教師出示題目：求圖1中草坪的面積，畫一畫，算一算，把能想到的方法都記錄下來。

2.交流匯報

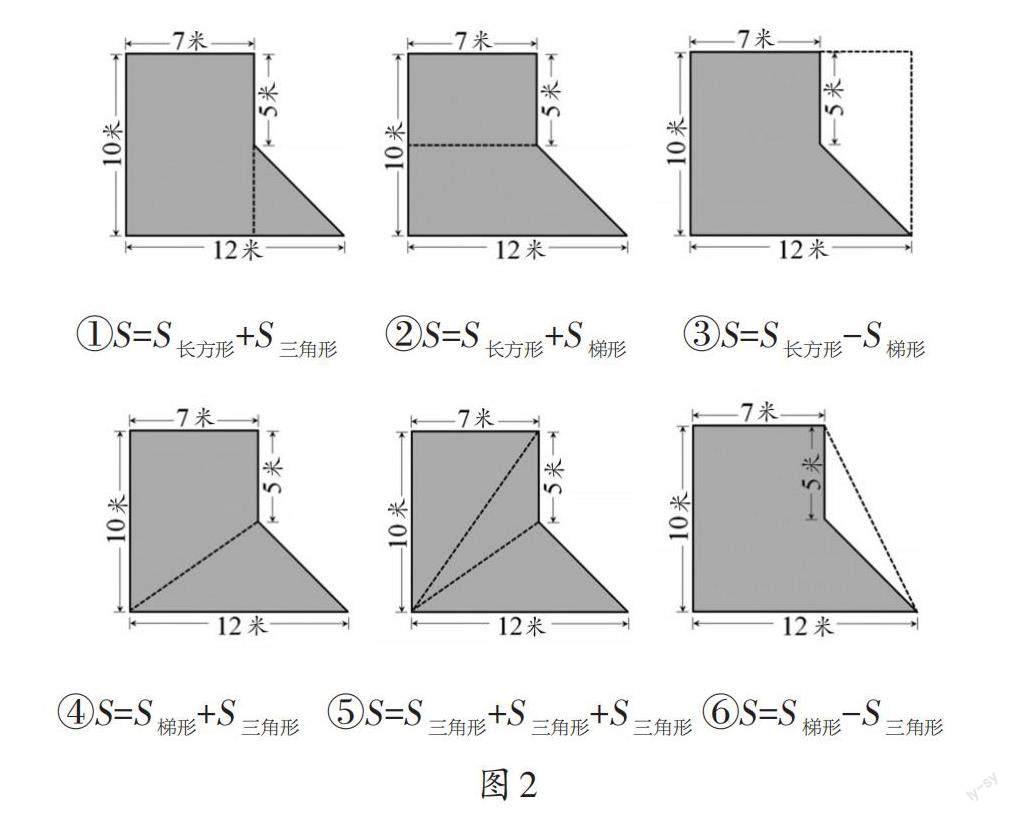
讓學生展示不同的思考方法（如圖2），并交流：①添加的輔助線的位置在哪里？②轉化成什么圖形？③轉化后的圖形根據哪些信息求面積？

3.比較方法

通過交流，學生發現：不管用哪種方法，計算結果都是82.5平方米。（教學過程略）

教師進一步引導學生思考：不同方法之間有什么聯系和區別？

學生發現：就像方法⑤可以優化為方法④，所有方法都是將未知的不規則圖形轉化為已知的基本圖形后求面積的。

4.方法提煉

根據不同的方法進行分類：一類是先將原圖分割成基本圖形，再相加求得組合圖形的面積，如方法①、方法②、方法④、方法⑤，稱為“分割法”；另一類是將原圖先拼補成一個基本圖形，再相減得到組合圖形的面積，如方法③、方法⑥，稱為“拼補法”。利用分割法、拼補法能巧妙求得組合圖形的面積。

二、審辨說理，反思修正

1.觀察分析

圖3是佳佳解決這個問題的過程，你同意佳佳用的計算方法嗎？

2.審辨說理

學生判斷出佳佳用的計算方法有誤后，引導全班討論、審辨，發現錯誤的原因為A、C、D三點不在同一條線段上，圖形ACDE不是三角形而是四邊形。

3.反思修正

為了得到正確的結果，有學生提出繼續分割圖形，連接CE，將整個圖形分割成三個三角形，再進行計算（如圖4）。

三、變式應用，能力提升

1.獨立思考

教師出示題目：計算圖5中各圖陰影部分的面積。

2.匯報交流

（1）關注整體：第①題引導學生整體觀察，發現ABCD是一個梯形，直接用公式計算面積，突出對圖形整體的把握。

（2）關注細節：第②題引導學生抓住關鍵細節45°和直角，嘗試用拼補法將組合圖形轉化為等腰直角三角形CDH和等腰直角三角形ABH，并計算面積差（如圖6）。

（3）關注聯系：第③題引導學生巧妙利用圖形邊和角的特征，先分割再拼補，將直角三角形BCE旋轉至直角三角形BAF的位置，從而將組合圖形轉化為一個正方形（如圖7）。

以上教學過程，學生在操作和分類中提煉方法，在審辨和反思中深入理解計算方法，在變式和拓展中提升能力，有效構建了解決組合圖形面積問題的基本方法，發展了空間觀念。

（浙江省杭州市天長小學）