虛擬元方法求解混合邊界條件下的線彈性問(wèn)題

馬俊馳, 程新博, 梁曉坤

(遼寧師范大學(xué) 數(shù)學(xué)學(xué)院,遼寧 大連 116081)

線彈性問(wèn)題在材料科學(xué)、橋梁結(jié)構(gòu)、土木工程和航空航天[1-3]等領(lǐng)域具有廣泛的應(yīng)用.目前線彈性問(wèn)題已有多種數(shù)值求解方法,如有限元方法[4]、有限差分法[5]、有限體積法[6]、弱有限元方法[7]、虛擬元方法[8]等.有限元方法在我國(guó)最早是由馮康先生[9]提出的,并形成一套系統(tǒng)的數(shù)值計(jì)算方法.有限元方法概念清晰、描述簡(jiǎn)單、應(yīng)用廣泛,但在剖分單元的選擇上具有一定的局限性,比如多邊形(多面體)網(wǎng)格,而虛擬元方法[10]在網(wǎng)格處理上具有較好的靈活性,其作為有限元方法的推廣受到廣泛關(guān)注.本文主要研究應(yīng)用虛擬元方法求解二維混合形式線彈性問(wèn)題,對(duì)于該問(wèn)題可以加強(qiáng)應(yīng)力張量的對(duì)稱(chēng)性,這種方法的挑戰(zhàn)在于混合形式線彈性問(wèn)題的離散化.文獻(xiàn)[11]中對(duì)應(yīng)力張量的對(duì)稱(chēng)性進(jìn)行了弱化,引入旋轉(zhuǎn)張量作為另一個(gè)未知數(shù),主要討論具有齊次Dirichlet邊界條件的二維線彈性問(wèn)題.而本文將邊界條件推廣到Dirichlet和Neumann的混合邊界條件.文獻(xiàn)[12]研究具有混合邊界條件的二維線彈性問(wèn)題的三種弱形式,給出虛擬元離散化的一般過(guò)程,并沒(méi)有給出詳細(xì)的虛擬元空間構(gòu)造、誤差估計(jì)等,本文將研究具有混合邊界條件的弱對(duì)稱(chēng)形式的線彈性問(wèn)題.

1 連續(xù)性問(wèn)題

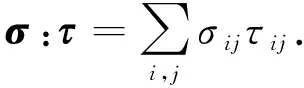
定義Ω?2為具有Lipschitz連續(xù)邊界的有界區(qū)域,邊界為Γ=?Ω,且Γ的兩個(gè)子集ΓD,ΓN滿足Γ=ΓD∪ΓN,ΓD∩ΓN=?.記彈性體所受外力的單位體密度為f∈[L2(Ω)]2.線彈性問(wèn)題可表述為,求σ,u滿足

(1)

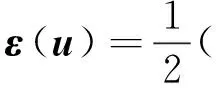
2 虛擬元方法

2.1 變分形式

定義空間Σ:=H(div;Ω),U:=[L2(Ω)]2,X:={Υ:Υ∈[L2(Ω)]2×2,Υ反對(duì)稱(chēng)}.

通過(guò)分部積分法,得到問(wèn)題(1)的變分形式:找到(σ,u,ω)∈Σ×U×X,使得

(2)

據(jù)文獻(xiàn)[13]得雙線性形式a(·,·)滿足連續(xù)性和強(qiáng)制性,b(·,·),c(·,·)滿足inf-sup條件,則問(wèn)題(2)的解存在且唯一.

2.2 構(gòu)造虛擬元空間

首先對(duì)區(qū)域Ω進(jìn)行剖分,設(shè){Th}h是將Ω分解為元素E的序列,h表示{Th}h中元素的最大直徑.假設(shè)存在整數(shù)N和正實(shí)數(shù)β,使得對(duì)于每個(gè)h和每個(gè)E∈{Th}h,滿足:①E的邊數(shù)小于等于N;②E的最短邊與E的直徑hE之比大于β;③E相對(duì)于半徑為βhE的球上的每個(gè)點(diǎn)呈星形.

對(duì)于整數(shù)k≥1,定義局部應(yīng)力空間為

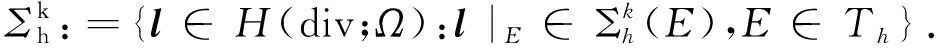
為了對(duì)誤差進(jìn)行估計(jì),引入下列投影算子與插值算子.

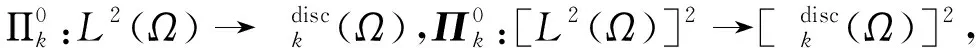
(3)

(4)

對(duì)于足夠光滑的函數(shù)q和l,以下估計(jì)成立

(5)

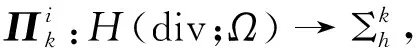
在每個(gè)單元E上,

(6)

2.3 虛擬元離散

基于上述剖分以及空間的定義,首先將雙線性形式進(jìn)行離散,

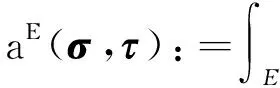
由于雙線性形式b(·,·),c(·,·)可以通過(guò)選擇適當(dāng)?shù)目臻gΣh,Uh,Xh來(lái)計(jì)算,所以不需要引入全局項(xiàng)b(·,·),c(·,·)的任何近似值,即bh(·,·)=b(·,·),ch(·,·)=c(·,·).

變分形式(2)的離散格式為:找到(σh,uh,ωh)∈Σh×Uh×Xh,使得

(7)

其中,div Σh?Uh.

上述的局部離散雙線性形式具有以下的3種性質(zhì).

引理1[16]存在整數(shù)k≥1,對(duì)于所有的E∈Th,都有[Pk(E)]2×2?Σh|E,

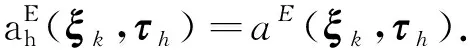
(2) 穩(wěn)定性:存在兩個(gè)不依賴(lài)于h和E的正常數(shù)α*和α*,使得

根據(jù)引理可知離散雙線性形式ah(·,·)具有連續(xù)性、強(qiáng)制性,b(·,·),c(·,·)滿足離散inf-sup條件,則離散形式(7)的解存在且唯一.

2.4 誤差分析

根據(jù)文獻(xiàn)[11]可得離散問(wèn)題的收斂性,下面對(duì)離散問(wèn)題的誤差進(jìn)行分析.

引理2[13]存在一個(gè)常數(shù)C>0,使得

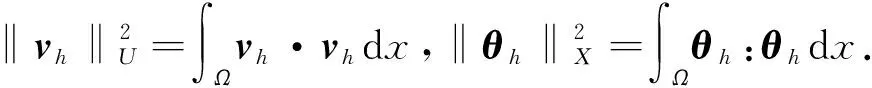
對(duì)于誤差分析,給出如下定理并證明.

定理1問(wèn)題(7)有唯一解(σh,uh,ωh)∈Σh×Uh×Xh,L2誤差估計(jì)為

‖σ-σh‖0+‖u-uh‖0+‖ω-ωh‖0≤C(μ)(hk+1‖σ‖k+1+hk+1‖u‖k+1+hk+1‖ω‖k+1),

其中,C(μ)是一個(gè)與λ無(wú)關(guān),但依賴(lài)于μ的正常數(shù).

根據(jù)問(wèn)題(2)和問(wèn)題(7),為了方便起見(jiàn),這里取gD=0,有

ah(eσ,τh)+b(τh,eu)+c(τh,eω)=

(8)

(9)

(10)

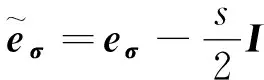
(11)

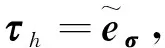
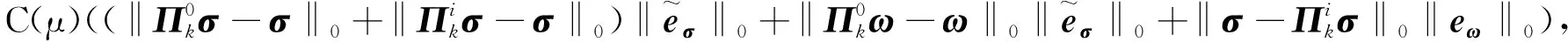
再根據(jù)式(11)有

(12)

令引理2中vh=0,θh=eω得到τh∈Σh滿足c(τh,eω)≥C‖τh‖0‖eω‖0,由式(8)有

(13)

根據(jù)式(12),式(13)得到估計(jì)

接下來(lái),根據(jù)三角不等式和式(5),式(6)可以推得

‖σ-σh‖0+‖ω-ωh‖0≤C(μ)(hk+1‖σ‖k+1+hk+1‖ω‖k+1).

(14)

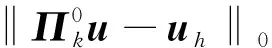
(15)

根據(jù)問(wèn)題(15)以及式(4),式(8)和τ的對(duì)稱(chēng)性有

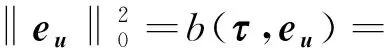
其中,

接下來(lái)由一致性、連續(xù)性和式(14)可得

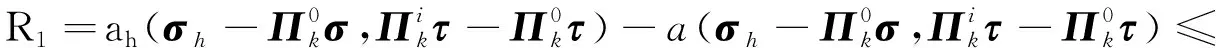
同理可得

R2≤C(μ)(hk+2‖σ‖k+1+hk+2‖ω‖k+1)‖eu‖0,

R3≤C(μ)(hk+2‖σ‖k+1+hk+2‖ω‖k+1)‖eu‖0,

將R1,R2,R3,R4代回原式,兩邊同時(shí)除以‖eu‖0就可以得到

(16)

由三角不等式和式(16)可得

‖u-uh‖0≤C(μ)(hk+1‖σ‖k+1+hk+1‖u‖k+1+hk+1‖ω‖k+1).

結(jié)論得證.

3 數(shù)值實(shí)驗(yàn)

本文考慮帶孔的板模型,其中,孔的半徑為a=0.4.考慮混合弱形式線彈性問(wèn)題(1),其中,彈性模量為E=103,泊松比為υ=0.3.弱對(duì)稱(chēng)形式經(jīng)過(guò)剛度矩陣的變換可化為強(qiáng)對(duì)稱(chēng)形式,即以位移和應(yīng)力作為問(wèn)題的解,因此數(shù)值實(shí)驗(yàn)中只考慮位移與應(yīng)力.根據(jù)文獻(xiàn)[17]可得,位移的精確解為

應(yīng)力的精確解為

其中,(r,θ)為極坐標(biāo),θ是從x軸的正半軸開(kāi)始沿逆時(shí)針?lè)较虻膴A角.對(duì)于平面應(yīng)變狀態(tài),κ=3-4υ.μ為L(zhǎng)amé常數(shù).

首先對(duì)區(qū)域進(jìn)行剖分,剖分區(qū)域?yàn)棣?Ω1/Ω2,其中,

圖1給出剖分區(qū)域Ω的多邊形網(wǎng)格剖分,其中,網(wǎng)格剖分?jǐn)?shù)n分別為46、539、3592和21916.

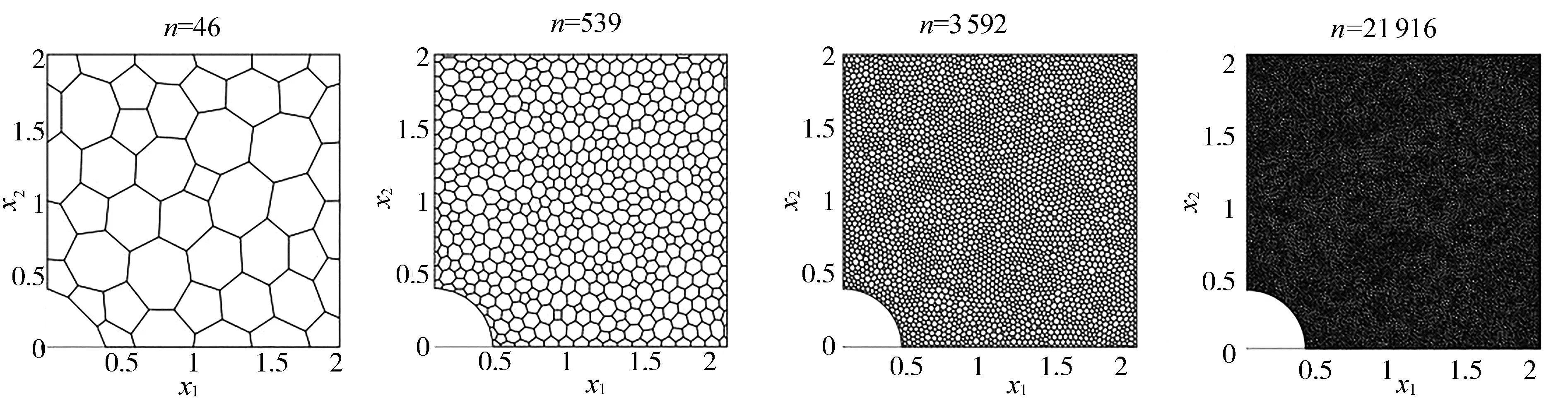
圖1 不同網(wǎng)格數(shù)對(duì)應(yīng)的剖分圖Fig.1 The division diagram corresponding to different mesh numbers

圖2給出網(wǎng)格剖分?jǐn)?shù)n為46、539、3592和21916的位移與應(yīng)力的數(shù)值解,其中,u1,h,u2,h為位移的數(shù)值解,σ11,h為應(yīng)力的數(shù)值解.

圖2 不同網(wǎng)格數(shù)對(duì)應(yīng)的位移與應(yīng)力的數(shù)值解Fig.2 Numerical solution of displacement and stress corresponding to different mesh numbers

其次應(yīng)用虛擬元方法求解上述線彈性問(wèn)題,得到數(shù)值解uh和σh與精確解u和σ之間的L2范數(shù)下的相對(duì)誤差,討論不同網(wǎng)格剖分?jǐn)?shù)下位移與應(yīng)力的相對(duì)誤差.

表1給出了不同網(wǎng)格剖分?jǐn)?shù)對(duì)應(yīng)的位移與應(yīng)力的相對(duì)誤差,其中,uerr(L2)表示L2范數(shù)下位移的相對(duì)誤差,σerr(L2)表示L2范數(shù)下應(yīng)力的相對(duì)誤差,其中,uerr(L2)=‖u-uh‖0,σerr(L2)=‖σ-σh‖0.

表1 不同網(wǎng)格數(shù)對(duì)應(yīng)的位移與應(yīng)力的相對(duì)誤差Table 1 Relative error of displacement and stress corresponding to different mesh number

從表1可以看出,隨著網(wǎng)格剖分?jǐn)?shù)的增加,位移與應(yīng)力的相對(duì)誤差都呈明顯減小的趨勢(shì),這與第三節(jié)的理論分析相一致,驗(yàn)證了誤差估計(jì)的有效性.

4 總 結(jié)

本文主要討論帶Dirichlet和Neumann混合邊界條件的二維線彈性問(wèn)題的虛擬元方法.線彈性問(wèn)題研究的是在一定假設(shè)條件下,彈性體受到外力或者其他外界作用時(shí),彈性體內(nèi)的應(yīng)力、應(yīng)變和位移之間的關(guān)系.本文研究混合弱形式的線彈性問(wèn)題,以位移、應(yīng)力和旋轉(zhuǎn)張量作為研究問(wèn)題的解,在混合邊界條件約束下,通過(guò)變分原理得到弱形式線彈性問(wèn)題的變分格式,然后通過(guò)構(gòu)造虛擬元空間和自由度對(duì)變分形式進(jìn)行離散.進(jìn)一步通過(guò)定義投影算子與插值算子處理誤差估計(jì),最后通過(guò)實(shí)際問(wèn)題帶孔的板,驗(yàn)證了理論分析的有效性.