基于分形理論的致密砂巖滲透率預測模型

宋澤章，呂明陽，趙力彬，張月巧，何元元，姜福杰，楊振中，陳偉業，霍利娜，王銳，梁驍

1.中國石油大學（北京）油氣資源與探測國家重點實驗室，北京 102249

2.中國石油大學（北京）地球科學學院，北京 102249

3.中國石油塔里木油田分公司勘探開發研究院，新疆庫爾勒 841000

4.中國石油勘探開發研究院，北京 100083

0 引言

2020 年，中國的致密砂巖氣總地質資源量為20.9×1012m3，是探明率（30.9%）最高的非常規天然氣[1]。從技術可采儲量、探明儲量、產量等角度來看，致密砂巖氣都是中國最現實、最應優先開采的非常規天然氣[2]。

致密砂巖的滲流能力一直是儲層質量評價及儲層分級的關鍵；而滲透率是直觀體現致密砂巖儲層滲流能力[3]并最終決定產能的最關鍵因素。滲透率的決定因素較多，如孔隙結構[4]、孔隙度[5]、成巖作用[6]等。在過去幾十年里，眾多學者基于各種實驗分析，建立了不同的模型來預測砂巖的滲透率[7-9]；它們可大體分為三類：基于高壓壓汞技術的滲透率預測模型、基于核磁共振技術以及基于分形幾何的滲透率預測模型。

高壓壓汞技術（HPMI）能夠直接提供眾多的孔隙結構參數。早在20 世紀40 年代，Purcell[10]就將毛細管壓力與氣測滲透率進行關聯。Winland 結合孔隙度與r35（進汞飽和度35%對應的孔喉半徑），建立了基于孔隙度與孔喉半徑的滲透率預測模型[11]。之后不同學者對此模型進行了改進，但變化主要體現在最優孔喉半徑的選取上，如值得注意的是，rapex模型沒有直接采用某一個進汞飽和度對應的孔喉半徑來做滲透率預測，而是基于Swanson 因子[14]，采用了孔喉連通性轉變節點對應的孔喉半徑。

與高壓壓汞技術相比，核磁共振技術（NMR）能夠定量評價自由流體和束縛流體，在表征流體滲流方面更有優勢。Coateset al.[15]發現砂巖的滲透率受控于可動流體與束縛流體體積比（FFI/BVI），進而對Timur 的滲透率預測模型[7]進行修正，提出了Timur-Coates模型；它 與SDR模型[16]以 及Prince-Rezaee 模型[3]是截至目前應用最為廣泛的、基于核磁共振技術的滲透率預測模型。其他NMR 滲透率預測模型多是基于Coates 模型或SDR[17]模型的改進模型。這些NMR滲透率模型在致密砂巖中的應用往往不如常規砂巖——它們采用的最優T2譜參數，如T2cutoff，T2gm和T2peak，僅能反映與這些T2譜參數相近的連通孔隙的滲流信息[18]；而致密砂巖孔隙結構復雜，非均質性強[19]，孔徑分布范圍更為廣泛。因此，亟需能夠表征更加寬泛孔徑范圍的參數用于滲透率預測。無論是基于最優孔喉半徑還是最優T2譜參數的滲透率模型，本質上均是僅選取了某一個特征孔喉半徑，結合孔隙度來預測滲透率，忽略了孔隙結構的非均質性，導致其在致密砂巖中的應用受限。

自20世紀末以來，Mandelbrot[20]提出的分形理論被廣泛用于儲層孔隙結構非均質性表征[21]。在一定的孔徑范圍內，致密砂巖的孔隙空間是自相似的，即存在“標度不變性”。借助分形維數可以表征更寬孔徑范圍的孔隙結構特征，這種自相似性可以通過分形維數來定量表征。Papeet al.[22]首先利用孔隙度和分形維數預測滲透率，而后研究人員[18]將該模型與Timur-Coates 模型、SDR 模型結合，建立了兩個基于NMR分形維數的滲透率預測模型，本研究簡稱Wu’s Timur-Coates 分形模型、Wu’s SDR 分形模型。目前，還鮮見基于高壓壓汞技術，使用分形理論建立的滲透率預測模型。

本研究優選塔里木盆地庫車坳陷巴什基奇克組致密砂巖為研究對象，綜合鑄體薄片、掃描電鏡、高壓壓汞技術、核磁共振技術和分形理論，定性、定量表征致密砂巖孔隙結構特征；在此基礎上，綜合對比經典滲透率預測模型與基于分形維數的滲透率預測模型對巴什基奇克組致密砂巖的適用性，以期確定最適用研究區的致密砂巖滲透率預測模型。

1 研究區地質概況

庫車坳陷位于塔里木盆地北部，其南北分別為塔北隆起和南天山造山帶，構造呈北東東向展布，面積約3.7×104km2[23]，包含八個次級構造——北部單斜帶、克拉蘇構造帶、依奇克里克構造帶、拜城凹陷、陽霞凹陷、烏什凹陷、秋里塔格構造帶、南部斜坡帶[24](圖1a)。克深次級構造帶位于克拉蘇構造帶中東部，整體呈近東西走向（東西向延伸約50 km）[25]。克深次級構造帶主要受北部邊界的克拉蘇斷裂與南部邊界的拜城斷裂控制[26]，背斜和斷層圈閉發育；本次研究區塊為KS2氣藏（圖1b）。

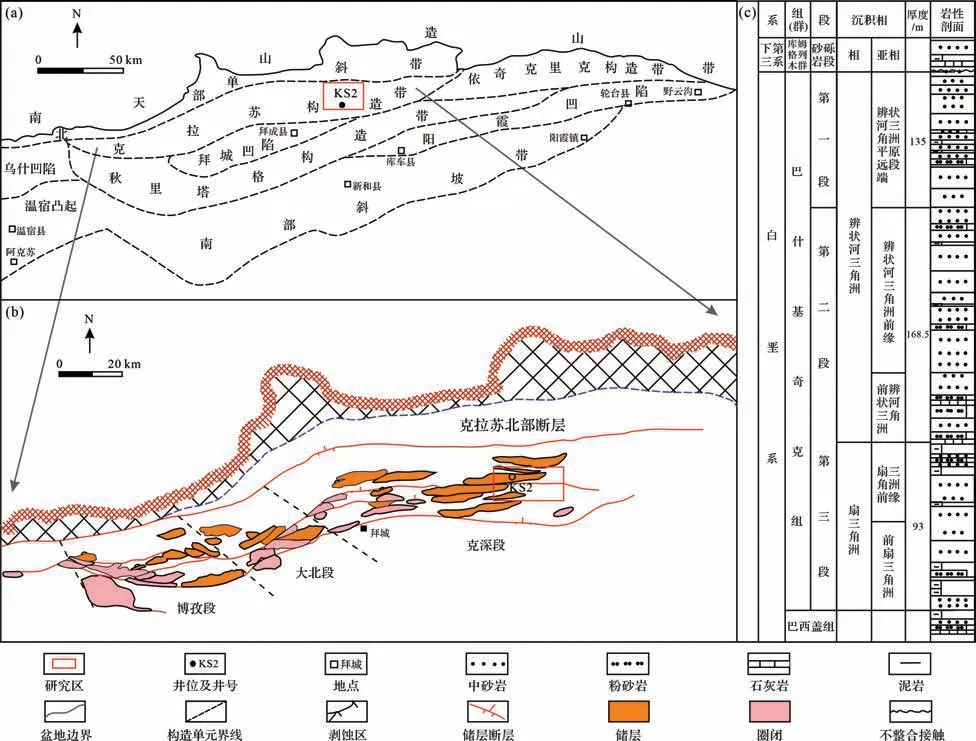
圖1 研究區地質背景（修改自文獻[24]）（a）庫車坳陷構造分區圖；（b）克拉蘇構造帶分區及研究區所在位置；（c）研究區地層柱狀圖Fig.1 Geologic background of the research area (modified from reference [24])(a) tectonic map of Kuqa Depression;(b) Kelasu tectonic belt and location of the research area;(c) comprehensive stratigraphic histogram of the research area

KS2 氣藏自下到上依次發育白堊系巴什基奇克組（K1bs）、庫姆格列木群（E1-2km）、古近系蘇維依組（E2-3s）、吉迪克組（N1j）、康村組（N1-2k）、康村組（N1-2k）以及第四系（Q）地層。研究目的層為白堊系巴什基克組；自下向上可劃分為3段：巴三段（K1bs3）、巴二段（K1bs2）巴一段（K1bs1）[27]；巖性以紅色—棕色細—中等粒度砂巖為主，夾雜礫巖；砂體總厚度為210～350 m。巴三段（K1bs3）發育三角洲前緣沉積亞相，與下伏巴西蓋組呈整合接觸[28]，發育中厚層細砂巖、薄層泥巖和粉砂質泥巖，厚度為70～83 m。巴二段（K1bs2）發育辮狀河三角洲前緣沉積亞相，以深棕色厚至超厚泥巖、粉砂質泥巖和粉砂巖為主，厚度為93～196.5 m。巴一段（K1bs1）與上覆膏鹽蓋層庫姆格列木群（E1-2km）呈不整合接觸，發育辮狀河三角洲前緣沉積亞相，由棕色至深棕色中巨厚砂巖組成，夾薄—中厚泥巖，厚度為47～70.5 m（圖1c）。研究樣品主要來自巴一段與巴二段。

2 實驗及滲透率預測模型

2.1 制樣和實驗分析測試

本次研究所用的30個致密砂巖樣品均來自塔里木盆地庫車坳陷巴什基奇克組1～2 段，埋深6 600～6 900 m。所有實驗均在塔里木油田分析測試中心完成。在分析測試前，先使用酒精與三氯甲烷配比抽提劑，提取樣品中的殘余油和鹽約36 h；然后在120 ℃恒溫箱中干燥24 h。孔隙度和滲透率采用美國CoreLab公司的CMS-300自動測試系統完成：孔隙度利用氦氣膨脹法在常壓下測量；滲透率使用壓力轉移法在約5.5 MPa圍壓下測量，并對滲透率測試結果進行克林肯伯格校正。高壓壓汞實驗采用美國Micromeritics 公司AutoporeⅣ 9510 全自動壓汞儀完成。儀器最大工作壓力414 MPa，可精確測量的孔喉半徑范圍為0.003～1 000 μm。基于Washburn 方程，高壓壓汞實驗可通過毛管壓力曲線獲得孔喉半徑分布（公式1）。

式中：Pc為毛細管壓力，MPa；σ為汞表面張力，空氣/汞的表面張力為485 mN/m；θ為接觸角，汞與各類物質間的接觸角為135°至150°之間，通常θ取=140°；r為孔喉半徑，nm。

核磁共振實驗采用英國Oxford Instruments 公司Maran Ultra 型核磁共振分析儀完成，儀器主頻強度為2 MHz，最小信噪比為100∶1，回波間隔為0.6 ms。干樣品抽真空處理后，使用189 098 mg/L NaCl 的模擬地層水進行加壓飽和，測量T2譜；而后在最佳離心力（15 000 轉，8.53 MPa）下進行高速離心，再次測量T2譜。離心實驗采用英國Oxford Instruments 公司OD-16R型高速離心機進行；保持1 h恒速離心，以盡可能離心可動流體。

2.2 滲透率預測模型

2.2.1 基于高壓壓汞技術的滲透率預測模型

應用最廣泛的基于高壓壓汞技術的滲透率預測模型為Winland模型，Rezaeeet al.[3]、Kolodzie[11]和Pittman[12]通過選取不同的特征孔喉半徑作為滲透率評價參數，對該模型進行了改進，三者的改進模型均可用式（2）來表達：

式中：K為滲透率，×10-3μm2；Ф為孔隙度，%；ri為累計汞飽和度i%對應的孔喉半徑，μm。Kolodzie、Pittman 和Rezaee 分別以累計進汞飽和度35%、25%、10%對應的孔喉半徑作為最優孔喉半徑參數，建立了r35、r25、r10滲透率預測模型。

與這些模型相差較大的另一個典型模型是Swanson 模型[14]，該模型引入了Swanson 因子（汞飽和度/毛管壓力的最大值）來預測滲透率：

式中：K為滲透率，×10-3μm2；SHg為累計汞飽和度，%；Pc為毛管壓力，MPa；m1、n2為系數。

Pittman 將Swanson 模型與Winland 模型結合，引入Swanson 因子對應的孔喉半徑rapex到Winland 模型中，建立rapex模型[12]：

式中：K為滲透率，×10-3μm2；Ф為孔隙度，%；rapex為汞飽和度/毛管壓力的最大值對應的孔喉半徑，μm。

2.2.2 基于NMR的滲透率預測模型

應用最廣泛的基于核磁共振技術的兩個滲透率預測模型是Timur-Coates 模型[29]（公式5）和SDR 模型[16]（公式6）：

式中：K為滲透率，×10-3μm2；Ф為孔隙度，%；FFI為自由流體體積，cm3；BVI為不可動流體體積，cm3。

式中：K為滲透率，×10-3μm2；Ф為孔隙度，%；T2gm為橫向弛豫時間的幾何均值，ms。

另一個經典模型是Prince-Rezaee 模型[3]，即式（7）

式中：K為滲透率，×10-3μm2；Ф為孔隙度，%；T2v為橫向弛豫時間的峰值，ms。

2.2.3 基于分形理論的滲透率預測模型

基于核磁共振技術，使用分形理論對Timur-Coates 模型與SDR 模型的改進[18]如公式（8）和（9）所示：

3 致密砂巖儲層特征

3.1 物性特征

研究區30個巴什基奇克組致密砂巖樣品氣測孔隙度（氦氣）介于2.9%～8.4%，平均值和中值分別為5.29%和4.97%；克氏滲透率變化很大，相差多個數量級（0.003～0.678×10-3μm2），平均為0.036×10-3μm2，中值為0.013×10-3μm2；屬典型的特低孔、超低滲致密砂巖儲層（圖2a，b）。孔隙度與滲透率的對數之間線性相關關系較差（R2=0.5），指示孔隙結構的非均質性較強（圖2c）。

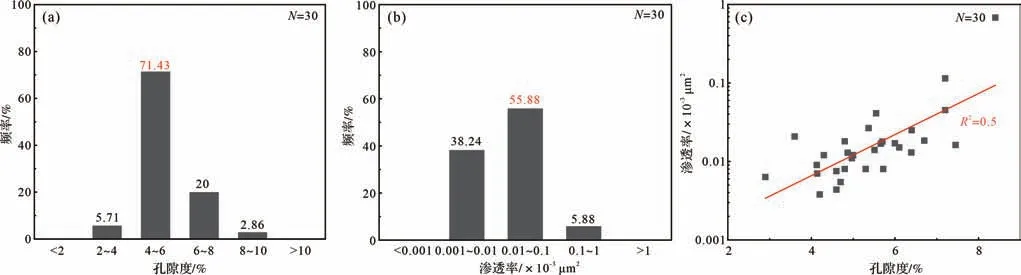
圖2 KS2 氣藏巴什基奇克組致密砂巖物性特征（a）孔隙度分布頻率直方圖；（b）滲透率分布頻率直方圖；（c）孔隙度與滲透率交匯圖Fig.2 Physical characteristics of the Bashijiqike tight sandstone from the KS2 gas reservoir(a,b) distribution frequency histograms of porosity and permeability;(c) intersection of porosity and permeability

3.2 孔隙類型

KS2 氣藏巴什基奇克組致密砂巖以細—中砂巖為主，分選中等；碎屑顆粒呈次圓—次棱角狀，以線接觸和凹凸接觸為主（圖3a）、鑲嵌膠結，結構成熟度較低。孔隙空間以粒間孔、溶蝕孔與晶間孔為主；整體上微裂縫不太發育，鏡下僅在局部區域出現（圖3a），且多因膠結而封閉。殘余粒間孔和溶蝕孔是研究區巴什基奇克組儲層最主要的孔隙類型：殘余粒間孔是原生孔隙經強烈的壓實作用而形成，多被自生石英、自生長石、白云石及自生/碎屑黏土填充（圖3b），以微米級孔隙為主；溶蝕孔多是骨架顆粒中的不穩定礦物受到不同程度溶蝕，在粒內或粒間形成大小不等、圓形和港灣狀，多為納米—微米級孔隙（圖3c）。晶間孔多由黏土礦物提供：自生黏土礦物（自生伊利石、自生伊利石/蒙脫石混合層）以搭橋式在顆粒孔隙間垂直生長，形成黏土礦物渡橋，其間發育晶間孔，呈不規則狀，主要為納米級孔隙（圖3d）。

圖3 KS2 氣藏巴什基奇克組致密砂巖微觀特征（a）線接觸與微裂縫，KS215井，6 725.44 m；（b）粒間孔，KS215井，6 730.77 m；（c）長石溶蝕孔，KS223井，6 805.63 m；（d）晶間孔，KS215井，6 741.77 mFig.3 Microscopic characteristics of the Bashijiqike tight sandstone from the KS2 gas reservoir(a) line contact and micro-fracture,well KS215,6 725.44 m;(b) intergranular pores,well KS215,6 730.77 m;(c) dissolution intergranular pores developed in the feldspar,well KS223,6 805.63 m;and (d) intercrystalline pores,well KS215,6 741.77 m

3.3 孔隙結構特征

研究區18個巴什基奇克組致密砂巖樣品的高壓壓汞結果表現出良好的相似性：（1）最大進汞飽和度值很高（圖4a），為98.55%～100%，平均為99.61%；（2）進汞段曲線具有較為明顯的“平臺段”，表明孔徑分布具有明顯的主峰（圖4b）且主峰多落于納米級孔徑區間；（3）儲層主要流動孔隙半徑（累計滲透率貢獻值達95%的孔隙半徑均值）為0.14～3.19 μm（平均為0.53 μm）；（4）不同樣品的排驅壓力差異大，從0.2 MPa 至3.51 MPa 不等，平均為2.24 MPa，以高排替壓力樣品為主，反映儲層的致密特性。

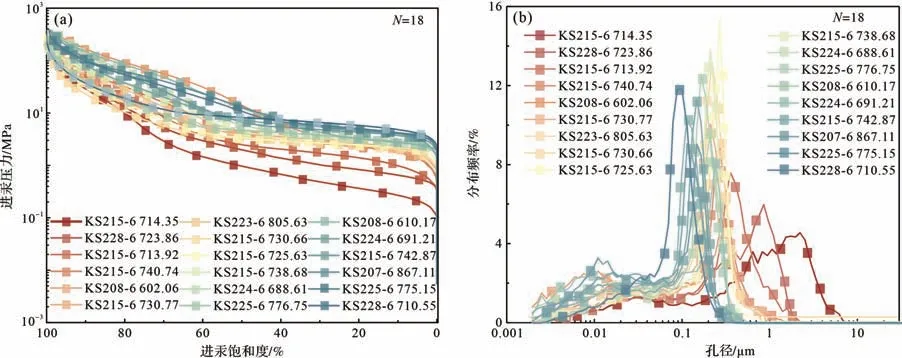
圖4 KS2 氣藏巴什基奇克組致密砂巖孔隙結構高壓壓汞表征（a）毛細管壓力曲線；（b）孔徑分布曲線Fig.4 Pore structure characterization using a high-pressure mercury intrusion experiment for the Bashijiqike tight sandstone from the KS2 gas reservoir(a) capillary pressure curve;(b) pore size distribution of nuclear magnetic resonance (NMR)

核磁共振結果顯示，核磁共振T2譜（圖5a）形態各異：單峰、雙峰、三峰均存在，反映致密砂巖孔隙結構非均質性強；核磁共振孔徑分布曲線（圖5b）跨度大——從小于一納米至數微米，但以納米級孔隙為主。

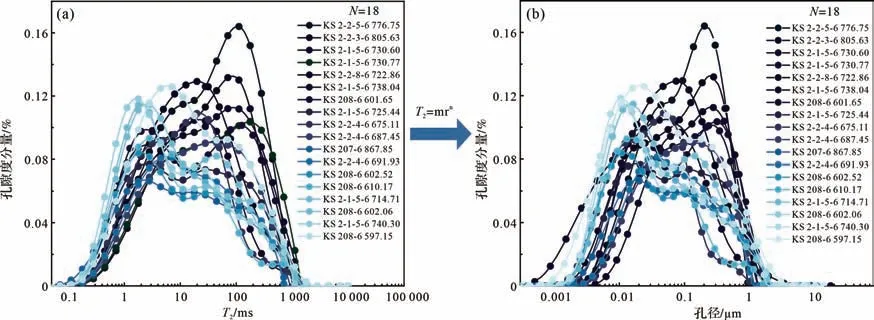
圖5 KS2 氣藏巴什基奇克組致密砂巖孔隙結構核磁共振分析（a）核磁共振T2譜；（b）核磁共振孔徑分布曲線Fig.5 NMR analysis of the pore structure of the Bashijiqike tight sandstone from the KS2 gas reservoir(a) NMR T2 spectrum;(b) pore size distribution of NMR

3.4 孔隙非均質性特征

基于高壓壓汞[19]與核磁共振數據對巴什基奇克組致密砂巖的孔隙結構分別進行分形分析（圖6）：在雙對數坐標軸上，高壓壓汞與核磁共振的數據點均呈分段線性分布，指示在不同的孔徑范圍內，致密砂巖孔隙結構存在不同的分形特征，需對其進行分段分形分析。

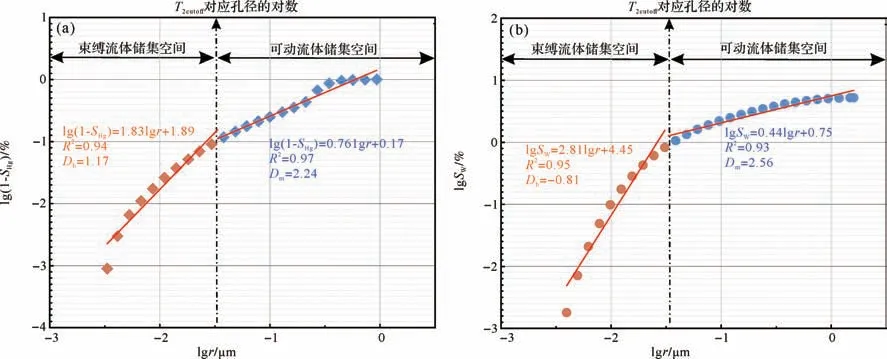
圖6 KS2 氣藏巴什基奇克組致密砂巖儲層孔隙結構分形分析（a）基于高壓壓汞數據的孔隙結構分形分析，KS215井，6 730.60 m；（b）基于核磁共振數據的孔隙結構分形分析，KS215井，6 730.60 mFig.6 Fractal analysis of the pore structure of the Bashijiqike tight sandstone from the KS2 gas reservoir(a) fractal analysis of pore structure based on HPMI,well KS215,6 730.60 m;(b) fractal analysis of pore structure based on NMR,well KS215,6 730.60 m

前人基于核磁共振數據進行分段分形分析時，常采用T2cutoff值對應的孔隙半徑（rcutoff）的對數作為不同分形段的分界點[30]。孔徑大于rcutoff的孔隙為大孔（對應的分形維數用Dm表示），是可動流體的主要儲集空間；孔徑小于rcutoff的為小孔（對應的分形維數用Db表示），是束縛流體的主要儲集空間。以KS215井6 730.60 m 樣品為例（圖6），各分形段線性擬合系數均很高（R2＞0.80），指示分形模型的有效性；Db均小于2，表明小孔不具備分形特征；基于高壓壓汞和核磁共振得到的大孔Dm變化范圍分別為2.41～2.80 和2.41～2.74，指示孔隙結構具有較強的非均質性。

4 滲透率預測模型綜合對比

常用的用于評價預測模型準確性的指標有：MSE（均方誤差）、RMSE（均方根誤差）、MAPE（平均絕對百分比誤差）、MAE（平均絕對誤差）；其中，RMSE和MAPE應用最為廣泛。RMSE體現了預測值與實際值之間的偏差；而MAPE 表示平均絕對百分比誤差。由于滲透率變化范圍大（跨數量級），為了更好地評價滲透率預測模型的準確性，既要考慮均方根誤差（絕對值），也要考慮平均絕對百分比誤差（相對值）。為此，本研究對RMSE和MAPE進行歸一化，引入精度指數（ACI：Accuracy Index）[5]：

式中：Er為滲透率預測模型的誤差合集；Ermin為誤差合集中每一項的最小值；Ermax為誤差合集中每一項的最大值。

為驗證滲透率模型的有效性，將18 個樣品數據隨機地分為兩組：測試集（6 個樣品）和驗證集（12 個樣品）；以測試集的數據進行多元線性擬合，求取滲透率模型中的系數（a，b，c），確定滲透率模型；用剩余的12個樣品數據對模型的有效性進行驗證。

4.1 基于高壓壓汞技術的滲透率預測模型

r35、r25、r10、rapex和Swanson 五個基于高壓壓汞技術的滲透率預測模型對比結果（圖7）顯示：預測精度最高的是rapex模型（ACI為0.60），最低的是r35和Swanson模型（ACI 為0.05）。值得注意的是，r35、r25、r10三個模型預測精度逐漸變高；它們之間的差異僅體現在最優孔徑ri值的選取上——隨著ri值的增大，預測效果顯著增強。以KS228 井6 723.86 m 樣品為例，其r35、r25、r10對應的毛細管半徑分別為0.63 μm、0.81 μm、1.14 μm，而該樣品的主要流動孔隙半徑為1.08 μm，與r10最為接近——ri越接近主要流動孔隙半徑，則ri模型的預測精度越高。然而，r10模型的預測效果依然不如rapex模型，這可能是由于rapex為孔隙連通性較差的小孔向連通性較好的大孔轉變的節點[31]，是更能體現儲層流動特征的參數。因此，使用rapex能夠進一步提高滲透率預測模型的精度。

圖7 基于高壓壓汞的滲透率預測模型精度分析（a）r35模型；（b）r25模型；（c）r10模型；（d）Swanson模型；（e）rapex模型Fig.7 Accuracy analysis of the permeability prediction models based on high-pressure mercury injection (HPMI) data(a) r35 model;(b) r25 model;(c) r10 model;(d) Swanson model;and (e) rapex model

4.2 基于核磁共振技術的預測滲透率

Timur-Coates、SDR 和Prince-Rezaee 模型（圖8）預測效果均不理想。三個模型中，預測精度相對較高的是Timur-Coates模型和SDR模型（ACI 僅為0.50），最低的是Prince-Rezaee 模型（ACI 為0.44）。一般來說，基于核磁共振的滲透率預測模型多用于評價分選良好、孔隙發育的疏松砂巖[18]，往往要求滲透率和孔隙度之間存在較為緊密的相關關系；而巴什基奇克組致密砂巖不僅低孔、超低滲，孔隙結構還十分復雜、非均質性強，孔隙度和滲透率對數之間的相關關系較差（R2=0.5，圖2c），影響了模型的精度。

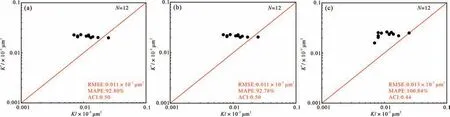
圖8 基于核磁共振的滲透率預測模型精度分析（a）Timur-Coates模型；（b）SDR模型；（c）Prince-Rezaee模型Fig.8 Accuracy analysis of the permeability prediction models based on NMR data(a) Timur-Coates model;(b) Schlumberger Doll Research Center (SDR) model;(c) Prince-Rezaee model

4.3 基于分形理論的滲透率預測模型

與核磁共振滲透率預測模型結果相似，Timur-Coates 分形模型和SDR 分形模型[18]在巴什基奇克組致密砂巖中的應用效果均不理想（ACI分別為0.05與0.10，圖9）。

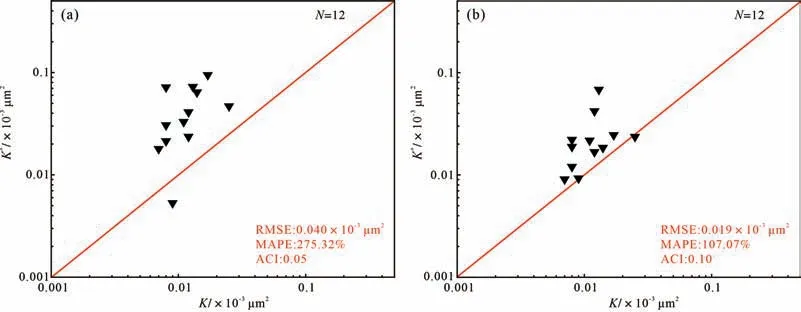
圖9 基于核磁共振的分形滲透率預測模型精度分析（a）Timur-Coates分形模型；（b）SDR分形模型Fig.9 Accuracy analysis of the fractal permeability prediction models based on NMR data(a) Timur-Coates fractal model;(b) SDR fractal model

值得注意是，分形模型中的D是以核磁共振的rcutoff為分界點進行分段分形分析求取的[18]。同樣，以KS215井6 730.60 m樣品為例，該樣品T2cutoff值對應的孔隙半徑為33 nm；而離心實驗采用的離心力為8.53 MPa，結合Washburn方程，同樣大小的毛細管力對應的孔隙半徑為17.05 nm（可動流體下限）。需要注意的是，離心前后的流體分布（圖10a）顯示：與33 nm相比，17.05 nm線可以更好地表征可動流體下限——右側的可動流體更多（達到96%）。與之相比，T2cutoff值忽視了部分小孔隙對滲流的貢獻（圖10b），這可能對滲透率模型的精度產生一定影響。值得注意的是，可動流體下限（17.05 nm）右側的大孔內仍存在大量束縛水，這是由于“墨水瓶孔”或頸喉存在導致的[32]。此外，前人基于分形理論的模型雖然考慮了孔隙結構非均質性對滲透率的影響，但本質上仍是以孔隙度預測滲透率，這可能也是模型預測精度較低的原因之一。

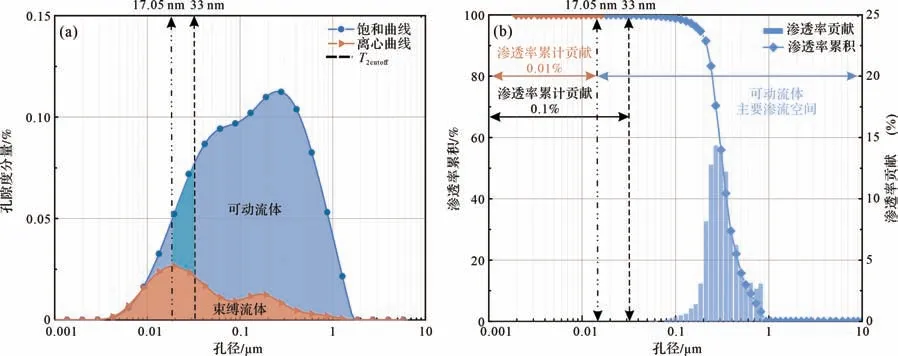
圖10 巴什基奇克組致密砂巖儲層可動流體儲集及滲流的孔隙空間特征（a）核磁共振離心前后PSD，KS215井，6 730.60 m；（b）高壓壓汞測得滲透率貢獻圖，KS215井，6 730.60 mFig.10 Characteristics of movable fluid accumulation and seepage of sandstone reservoirs from the Bashijiqike Formation(a) pore size distribution before and after centrifugation for NMR,well KS215,6 730.60 m;(b) proportion of penetration rate contribution for HPMI,well KS215,6 730.60 m

綜上，對前人的分形滲透率模型進行改進：以最大離心力對應的毛細管半徑（17.05 nm）的對數作為分段分形分析的分界點，而后選取Dm進行滲透率預測模型建模；在此基礎上，從孔隙結構的角度出發，以分形維數為基礎，重構致密砂巖滲透率模型。

大量研究表明，滲透率與分形維數的冪數呈較好的相關關系（R2＞0.6）[33-35]：

式中：K為滲透率，×10-3μm2；D為分形維數。

與公式（12）相似，Winland模型與SDR模型中滲透率與孔隙度的冪數也存在相關關系，因此將式（12）分別與式（2）、式（6）結合，用Dm替代孔隙度，建立兩種針對高壓壓汞數據與核磁共振數據的、基于分形理論的滲透率預測模型（式13，14）：

為選取最優的ri和T2gm，使用累計汞飽和度10%～60%（間隔5%）對應的孔隙半徑和T2＞1 ms、＞5 ms、＞10 ms、＞20 m～＞100 ms（間隔20 ms）的幾何均值進行對比；對K、Dm與不同ri、(T2gm)＞i做多元線性回歸分析，建立滲透率預測模型。誤差分析對比結果顯示：當ri取r20（式15）、T2gm取T2gm(＞40)（式16）時，滲透率預測模型的精度最高：

式中：K為滲透率，×10-3μm2；Dm為可動流體儲集及滲流空間的分形維數；r20為累計進汞飽和度20%所對應的孔隙半徑，μm；(T2gm)＞40為T2＞40 ms范圍內的幾何均值，ms。

與前人的滲透率預測模型（圖7～9）相比，本研究改進的滲透率預測模型精度更高：r20分形模型的ACI為0.85（圖11a），為所有預測模型中預測精度最高的（與rapex模型ACI 值相比，改進模型的ACI 提升了42%）；SDR（＞40）分形模型（ACI 為0.72）預測精度（圖11b）僅次于r20分形模型（與rapex模型ACI值相比，改進模型的ACI提升了20%）。

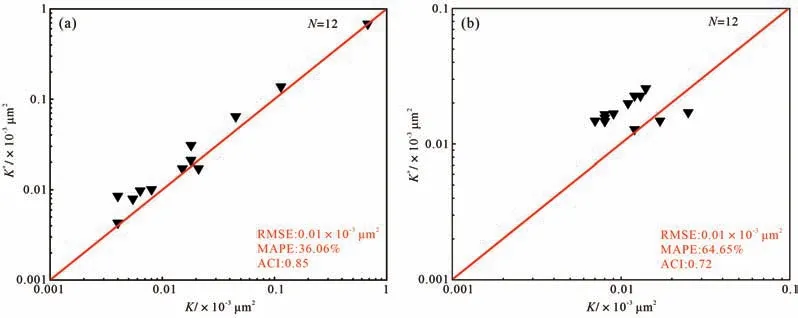
圖11 基于高壓壓汞（a）和核磁共振（b）的改進的分形滲透率預測模型精度分析（a）r20分形模型;（b）SDR(＞40)分形模型g.11 Accuracy analysis of the modified fractal permeability prediction models based on HPMI (a) and NMR (b) data(a) r20 fractal model;(b) SDR(＞40) fractal mode

r20分形模型ACI提升程度：

本研究提出的改進的分形滲透率預測模型的精度較之前的模型有所提升的原因，可能有以下幾個方面：（1）滲透率預測模型是基于分形維數建立的；分形維數具有“跨尺度”表征孔隙結構非均質性的特征[36]且分段分形中的Dm能夠較好地體現對滲透率有貢獻的孔隙結構信息；（2）選取了更合適的分段分形分析節點，計算得到的Dm更能表征可動流體儲集空間的非均質性，因而精度更高。此外，SDR(＞40)分形模型的預測精度低于r20分形模型的原因可能與“墨水瓶孔”或頸喉的存在有關，其大孔的分形段還包含了部分不可動流體所在孔隙（圖10a中）的信息，進而影響滲透率預測的精度。

5 結論

（1）與rapex模型相比，基于分形理論建立的r20分形滲透率預測模型、SDR(＞40)分形滲透率預測模型的預測精度分別提升了42%與20%。

（2）離心力對應的孔隙半徑（rcen）比核磁共振T2截止值對應的孔隙半徑（rcutoff）更適合作為分段分形分析的分界點，計算得到的Dm更能反映可動流體儲集空間的非均質性，更適于滲透率建模。

致謝 衷心感謝中國石油塔里木油田分公司勘探開發研究院提供的巖心和數據資料，以及審稿專家和編輯工作人員對本文提出的建設性修改意見。