核心素養(yǎng)視角下初中幾何課堂教學(xué)的探討和思考

楊蓓

筆者有一次參加全市初中某個(gè)年級(jí)的數(shù)學(xué)期末水平測(cè)試的閱卷工作，發(fā)現(xiàn)很多學(xué)生不會(huì)解答一道源于課本的變式題。為什么這么多學(xué)生不會(huì)解答？我們的幾何教學(xué)存在哪些問(wèn)題？如何才能更好地發(fā)展學(xué)生的幾何思維？核心素養(yǎng)視角下初中幾何課堂教學(xué)應(yīng)該如何改進(jìn)？圍繞這些問(wèn)題，我嘗試結(jié)合這道試題的答題情況對(duì)教學(xué)進(jìn)行反思。

一、學(xué)生錯(cuò)解中暴露的問(wèn)題

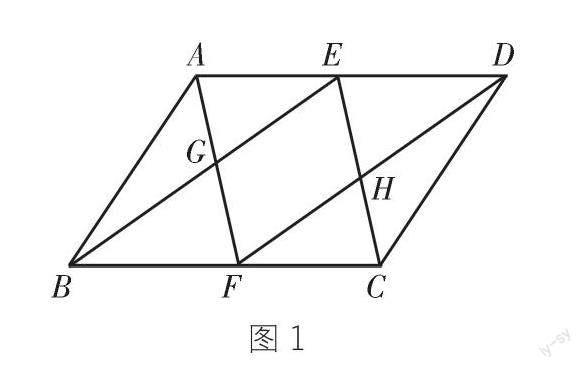
這道試題是這樣的：如下頁(yè)圖1，

ABCD中E、F分別是AD、BC中點(diǎn)，AF與BE交于點(diǎn)G，CE和DF交于點(diǎn)H。求證：四邊形EGFH是平行四邊形。

本題卷面分值7分。這道題是課本例題的變式，而且屬于幾何證明的基本題型，然而全市學(xué)生平均得分僅為3.41分。本題考查的內(nèi)容是平行四邊形的性質(zhì)與判定，屬于平行四邊形綜合題。我抽查了其中 1600 份試卷，分析這些學(xué)生的答案，發(fā)現(xiàn)正確解答本題的學(xué)生運(yùn)用了不同的證明方法完成了證明。其中，多數(shù)學(xué)生由平行四邊形的性質(zhì)得出一組對(duì)邊平行且相等，再由中點(diǎn)定義得到一組對(duì)邊平行且相等，從而完成證明；少數(shù)學(xué)生通過(guò)證明三角形全等來(lái)完成證明；還有少數(shù)學(xué)生通過(guò)作輔助線來(lái)完成證明。同時(shí)發(fā)現(xiàn)，除了部分學(xué)生完全沒(méi)有作答，相當(dāng)一部分學(xué)生寫(xiě)出的答案基本沒(méi)有呈現(xiàn)幾何證明的思維。學(xué)生在答題過(guò)程中出現(xiàn)的問(wèn)題主要表現(xiàn)在：隨意添加條件，盲目添加輔助線，過(guò)程表達(dá)不規(guī)范，定理理解不準(zhǔn)確，圖文不一致，思維定勢(shì)負(fù)遷移等。

二、基于學(xué)生錯(cuò)解的反思

為什么學(xué)生會(huì)出現(xiàn)上述各種各樣的錯(cuò)解？除了學(xué)生自身的原因之外，教師的教學(xué)設(shè)計(jì)是否存在問(wèn)題？我們的數(shù)學(xué)課堂教學(xué)應(yīng)該要注意什么？圍繞這些問(wèn)題，我針對(duì)學(xué)生的錯(cuò)解作了一些反思。

對(duì)于比較抽象的幾何知識(shí)的學(xué)習(xí)，如果教師不能采取正確的教學(xué)方式，沒(méi)有結(jié)合學(xué)生的認(rèn)知特點(diǎn)進(jìn)行教學(xué)，學(xué)生在接受新知識(shí)新方法時(shí)就會(huì)出現(xiàn)很大的困難。這就導(dǎo)致學(xué)生在解題的過(guò)程中容易因思維定勢(shì)出現(xiàn)錯(cuò)誤，并且相同的錯(cuò)誤總會(huì)重復(fù)出現(xiàn)，因此有必要回到課堂教學(xué)環(huán)節(jié)來(lái)查找原因。

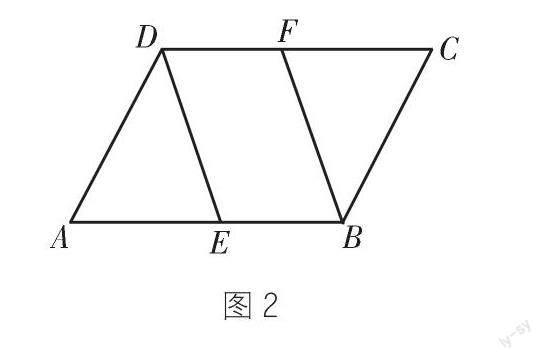
課本里有這樣一道例題：如圖2，在ABCD中，E、F分別是AB、CD的中點(diǎn)。求證：四邊形EBFD是平行四邊形。

我對(duì)本課時(shí)一些課堂實(shí)錄和教學(xué)視頻進(jìn)行整理研究，發(fā)現(xiàn)本節(jié)課的教學(xué)模式一般是“定理—例題—練習(xí)—習(xí)題”，通過(guò)變式訓(xùn)練強(qiáng)調(diào)定理的運(yùn)用。導(dǎo)致學(xué)生思維不規(guī)范、不完備、不靈活的原因，主要是有些教師忽視了學(xué)生的課堂主體地位，沒(méi)有給學(xué)生留出充分的思考時(shí)間和空間，也沒(méi)有回應(yīng)學(xué)生提出的質(zhì)疑。還比如有些教師在授課時(shí)思維不夠開(kāi)闊，回避學(xué)生提出的問(wèn)題，沒(méi)有讓學(xué)生經(jīng)歷用全等三角形證明邊角相等的過(guò)程。事實(shí)上，即使學(xué)生的方法比較復(fù)雜也是他們的一種經(jīng)歷，他們自己會(huì)比較和感悟各種方法的優(yōu)劣。有些教師沒(méi)有充分發(fā)揮典型例題的作用，沒(méi)有讓學(xué)生經(jīng)歷概念的發(fā)生、發(fā)展的過(guò)程，缺乏對(duì)學(xué)生思維能力進(jìn)行拓展的訓(xùn)練，導(dǎo)致學(xué)生形成思維定勢(shì)。

三、以深度思考促進(jìn)學(xué)生的思維

數(shù)學(xué)核心素養(yǎng)之一就是會(huì)用數(shù)學(xué)的思維思考現(xiàn)實(shí)世界。“圖形與幾何”的學(xué)習(xí)與幾何直觀、推理能力等素養(yǎng)的培養(yǎng)密切相關(guān)。

要在幾何教學(xué)中發(fā)展學(xué)生的幾何直觀和推理素養(yǎng)，必須把思考的時(shí)間和空間留給學(xué)生，讓學(xué)生經(jīng)歷、體驗(yàn)和享受自主發(fā)展數(shù)學(xué)思維的過(guò)程。

要讓學(xué)生掌握有效的思考方法，優(yōu)化自己的思維，必須讓學(xué)生在思考的過(guò)程中，在原有認(rèn)知的基礎(chǔ)上拓寬視野，在有關(guān)問(wèn)題上了解更多的知識(shí)，養(yǎng)成良好的思考習(xí)慣。

教師要引導(dǎo)學(xué)生把思維引向縱深，探索正確、有效、簡(jiǎn)潔的證明方法，將發(fā)展學(xué)生核心素養(yǎng)落實(shí)在課堂教學(xué)中，比如對(duì)于上述課本例題的教學(xué)可以進(jìn)行如下的改進(jìn)。

對(duì)于上述課本的例題，學(xué)生提出用全等三角形來(lái)證明時(shí)，教師可以引導(dǎo)學(xué)生進(jìn)一步探究，得出下列方案：

教師：用全等三角形如何證明？你能具體說(shuō)說(shuō)思路嗎？

學(xué)生1：由平行四邊形的性質(zhì)得出 ∠A=∠C，AD=BC，又因?yàn)锳E=CF，可證出ΔAED≌△CFB，從而得到DE=BF，又因?yàn)镈F=BE，即可證明四邊形EBFD是平行四邊形。

學(xué)生2：我連接 EF，由四邊形AEFD是平行四邊形，得出DF=AE，又因?yàn)锳E= BE，可得DF=BE，即可得出四邊形EBFD是平行四邊形。

此時(shí)學(xué)生有了從不同的角度來(lái)分析問(wèn)題、運(yùn)用多種方法來(lái)解決問(wèn)題的經(jīng)驗(yàn)，教師要通過(guò)小結(jié)引導(dǎo)學(xué)生的思維再往前走一步。“這幾種方法中，哪一種最好？為什么？”“平行四邊形的證明什么情況下可以利用三角形全等的特點(diǎn)，什么情況下可以利用平行四邊形定理？”

這樣的設(shè)計(jì)通過(guò)“一題多證”充分暴露學(xué)生思維活動(dòng)的特點(diǎn)，培養(yǎng)了學(xué)生思維的求同性，讓學(xué)生自己靈活選擇證明方法，提升學(xué)生對(duì)課程標(biāo)準(zhǔn)中“四基”的整體掌握程度，從而提高邏輯思維能力。

當(dāng)學(xué)生基本掌握了例題的解決方法后，課堂上可以進(jìn)一步安排思維跨度較大的題目，讓學(xué)生對(duì)問(wèn)題進(jìn)行深度思考。

回到本文開(kāi)頭的試題，在圖1的平行四邊形ABCD中，E、F分別是AD、BC的中點(diǎn)，連接AF、BE交于點(diǎn)G，連接CE、DF交于點(diǎn)H。

變式問(wèn)題1：當(dāng)四邊形ABCD是矩形時(shí)，四邊形EGFH是什么圖形？

變式問(wèn)題2：若將“E、F是AD、BC的中點(diǎn)”改為“AE＝BF”，其他條件不變，畫(huà)出相應(yīng)圖形，四邊形EGFH是平行四邊形嗎？

總之，核心素養(yǎng)視角下的初中幾何課堂教學(xué)，需要從傳統(tǒng)知識(shí)的傳授向培養(yǎng)學(xué)生的核心素養(yǎng)轉(zhuǎn)變，需要教師落實(shí)核心素養(yǎng)目標(biāo)，體現(xiàn)育人要求，引導(dǎo)學(xué)生掌握基本圖形的定義、性質(zhì)與判定方法等，增強(qiáng)學(xué)生發(fā)現(xiàn)問(wèn)題、提出問(wèn)題、分析問(wèn)題和解決問(wèn)題的能力，構(gòu)建由“葉”到“枝”的知識(shí)體系，提升學(xué)生的思維品質(zhì)，促進(jìn)學(xué)生形成理性思維和科學(xué)精神。

責(zé)任編輯 羅 峰