基于MIMO滑模的氣動伺服系統控制

王瀟, 孔建壽

(1. 南京理工大學 自動化學院,江蘇 南京 210094;2. 河北省農業生產資料集團有限公司,河北 石家莊 050041)

0 引言

氣動伺服系統憑借安全可靠、構造簡單等優點,廣泛應用于工業、農業等自動化領域[1-2]。但是由于空氣的可壓縮性、氣閥特性以及氣缸的摩擦等因素,使得氣動伺服系統的非線性較高,從而給氣動系統的精確控制帶來了較大的困難[3]。同時,氣動系統在工作中的一些外部擾動也會對其跟蹤性能產生影響。因此,保證氣動伺服系統跟蹤控制的性能,對于氣動系統的安全穩定運行有著至關重要的作用。

針對氣動系統的控制,國內外學者已經進行了相關研究。SMAOUI等[4]對基于氣缸的伺服系統進行了建模,并采用Backstepping算法實現了系統的位置控制,但是算法應用依賴于較為精確的系統模型,抗干擾能力不足。許翔宇、林黃耀、劉凱等采用LM算法對氣動系統的PID控制器參數進行整定,以提高系統響應,降低系統震蕩,基于PID的策略同樣也有相關應用[5-7]。雖然基于PID的方法不需要精確建模,但是系統的抗擾動能力不足。為了提高氣動系統的抗干擾能力,SHEN[8]采用滑模控制(sliding model control, SMC)策略,實現了氣動伺服系統的高性能跟蹤控制。在滑模控制的基礎上,進行算法的改進,同樣提高了氣動系統的魯棒性[9]。其他基于自適應控制以及自抗擾控制技術的氣動系統,同樣取得了較為出色的系統跟蹤控制能力[10-14]。

以上的氣動伺服系統通過控制器的設計都實現了較為出色的跟蹤控制效果,但是系統主要進行位置跟蹤,未對氣動系統的柔順性進行探討。由于氣體的可壓縮性,氣動系統具有內在柔順性。YI等[15]提出可以通過氣壓的調節,實現氣動系統輸出柔順性的整定。所以本文在進行軌跡跟蹤的基礎上,進行氣動系統柔順性的控制,實現系統的多輸入多輸出(multiple input multiple output, MIMO)。

本文針對氣動系統非線性的問題,提出采用MIMO SMC算法實現氣動伺服系統位置跟蹤和柔順性控制。首先對氣動系統進行基于流量控制策略的建模,然后將狀態空間轉換為嚴格反饋系統形式,在此基礎上進行SMC控制器的推導,最后通過仿真平臺對所提方法進行驗證。

1 氣動系統動力學模型

基于氣缸的氣動伺服系統如圖1所示。其中,氣缸左右兩個氣腔獨立工作,單獨由兩個比例流量閥進行控制。兩個氣腔內的壓力共同作用于活塞上,壓力差作用下產生運動力。

圖1 氣動伺服系統

該氣動伺服系統的動力學方程為

(1)

式中:M為傳動傳輸桿上的總質量;δ為活塞相對于平衡位置的距離,正向為圖1中的右向;τext為外部驅動力;P1和P2分別為左、右兩側氣腔內壓力;Sa表示氣壓力的作用面積,即活塞的面積。由動力學方程可知,對活塞的運動控制實際上是由左、右氣腔壓力的控制實現的。該驅動過程通常是采用比例壓力閥,經過直接調節內腔壓力來實現。該驅動策略簡單直接,但是以壓力快速響應為前提,忽略了內腔壓力變化的過程以及系統的動態效果。本文采取第二種驅動方式,即流動控制,通過比例流量閥調節進入氣腔的氣流量,進而實現對腔內壓力的動態跟蹤,這一過程的氣體動力學描述為

(2)

(3)

本文是通過氣流量的調節實現對壓力的調節,氣流量的調節過程為

(4)

式中:Ai表示比例流量閥的閥門開度,即為模型系統的控制輸入,Ai=-1表示閥門全開放氣,Ai=1表示閥門全開充氣。所以Ai∈[-1,1];Λi(Pu,Pd)為最大流量,是由上游壓力Pu和下游壓力Pd決定的,具體計算公式如下:

(5)

式中:C為氣流常數;ρ0為氣體密度;b為壓力系數;T0為環境空氣溫度;Tu為氣源空氣溫度,一般兩個溫度取相同。當充氣時,上游壓力Pu為氣源壓力,下游壓力Pd為氣囊內部壓力;放氣時,上游壓力Pu為氣囊壓力,下游壓力Pd為環境氣壓力。

式(1)—式(5)描述了整個氣動伺服系統的非線性動力學模型。為了便于進一步研究控制算法,將整體系統模型用狀態空間模型進行描述。

(6)

(7)

(8)

結合式(6)—式(8),氣動系統的非線性狀態空間模型描述為

(9)

(10)

(11)

對于系統輸出,除了進行常規要求的軌跡跟蹤,本文還增加了用于描述柔順特性的輸出量,即(P1+P2)/2。根據動力學方程可知,氣缸活塞的運動控制是通過(P1-P2)的壓力差實現的,而在保證壓力差的情況下,壓力P1和P2仍然可以自主調節。當P1和P2整體值較低時,氣體可壓縮性較高,活塞對外可表現出較低的剛度;反之,活塞對外可表現出較高的剛度。所以通過(P1+P2)/2的控制,可實現不同剛度表現。

最終構建式(9)所描述的系統模型,可以看出,這是一個非線性雙輸入、雙輸出的系統。所以本文采用MIMO SMC來對氣動系統進行控制。

2 MIMO SMC算法

2.1 坐標轉換

算法的研究在式(9)所描述的狀態空間模型上進行,但是為了規范化推導過程,一般需要將狀態空間模型轉換為嚴格反饋的形式。所以本文進一步使用Lie導數算子,對式(9)的模型進行坐標轉換,Lie導數的計算為:

(12)

(13)

(14)

由式(14)可推得

(15)

2.2 MIMO滑模控制

針對式(15)所描述的狀態空間模型,構建針對軌跡和氣壓的兩個滑模面為

(16)

(17)

為了便于分析,將滑模面導數中的向量和矩陣用符號代替為:

(18)

(19)

(20)

在式(17)的滑模面導數基礎上,選用經典的等速趨近率,構造系統的輸入為

(21)

滿足k1>0和k2>0。由得到的系統輸入和滑模面,可計算得Lyapunov方程的導數

(22)

因此,針對非線性氣動系統,基于MIMO SMC得到的系統雙輸入能夠使得系統滿足軌跡跟蹤和基于平均壓力的柔順性控制需求。

3 仿真分析

3.1 系統參數和仿真平臺

在已經建立的氣動系統模型和MIMO SMC控制算法的基礎上,本文在Simulink環境下進行仿真驗證,為后續的應用奠定基礎。其中為了模擬實際應用中的驅動物體實現往復運動,仿真設定伺服系統驅動質量為2kg。建模過程中涉及的其他模型參數如表1所示。

表1 系統仿真參數

基于選定的參數,建立如圖2所示的仿真模型。

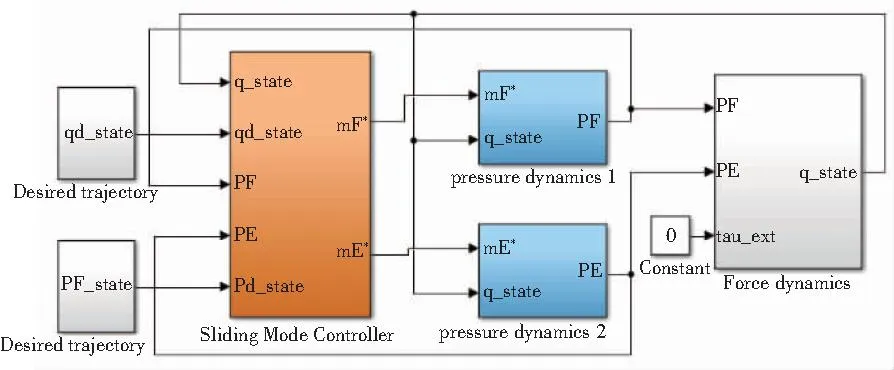
圖2 Simulink環境下的仿真模型

圖2中,分別給定期望軌跡和期望的用于柔順控制的壓力,經過MIMO SMC模塊后,得到兩個比例流量閥的開度,同時在此刻狀態下,進一步計算得到輸入到兩個氣腔的流量。在輸入流量下,由氣壓動力學計算的氣腔內壓,進而作用于活塞面,實現活塞桿的運動。

對于軌跡跟蹤,根據實際應用中往復的運動,以正弦信號為期望軌跡,具體給定幅值50mm,頻率1Hz和2Hz的正弦信號。其中,對于氣動系統,2Hz的正弦信號對于檢測系統性能具有重要意義。對于壓力,給定一個斜坡信號序列,以檢測系統在滿足軌跡跟蹤的同時,還具有柔順性調控的性能。

3.2 仿真結果和分析

正弦信號的軌跡跟蹤結果如圖3和圖4所示。其中,虛線為期望軌跡,實線為實際跟蹤軌跡。從圖中的對比可以看出,本文提出的算法能夠使得氣動系統準確地跟蹤上期望信號。需要注意的是,仿真環境中的誤差相對于給定信號值數值較低,可以忽略。雖然仿真是比較理想的工作狀態,但是本文仿真系統的參數都是根據實際工作系統設定的,且通過相關測定后給定,可以反映系統的真實性。

圖3 1Hz正弦信號跟蹤

圖4 2Hz正弦信號跟蹤

2Hz的信號對系統的響應性能要求較高,從圖4可以看出,系統仍能夠穩定跟蹤上2Hz正弦信號,跟蹤效果并未下降。

在保證軌跡跟蹤性能的基礎上,同時保證平均壓力的控制,對于給定的壓力斜坡信號,跟蹤效果如圖5所示。

圖5 壓力斜坡信號跟蹤

從圖5中可以看出,在初始50kPa穩定均壓后,系統能夠以斜坡的形式升壓到100kPa并保持穩定,在保證系統軌跡跟蹤效果的情況下,系統的剛度提升,柔順性降低。穩定后,在6s時,系統能夠對坡度更大的壓力進行控制;在7s時,壓力進一步升高到200kPa,此時系統達到一個較高的剛度,將會對外部位移干擾產生較高的恢復力。

根據軌跡跟蹤和壓力控制的仿真結果可以看出,本文所提算法能夠對構建的氣動伺服系統實現多輸入、多輸出的控制。

4 結語

本文在對非線性氣動系統進行完整建模的基礎上,采用MIMO SMC算法對系統軌跡跟蹤及柔順性進行同時控制,最后在搭建的仿真平臺上對系統進行了仿真分析,結果表明本文所提方法在保證軌跡跟蹤效果的同時,也實現了系統柔順性的壓力控制。整體工作為后續的應用奠定了基礎。