含干摩擦耗散結(jié)構(gòu)的非線性模態(tài)分析方法研究

王相乾

(南京航空航天大學(xué) 能源與動力學(xué)院,江蘇 南京 210016)

0 引言

干摩擦阻尼以其不受溫度限制、結(jié)構(gòu)簡單、減振效果明顯的特點而廣泛應(yīng)用于摩擦葉片、空間結(jié)構(gòu)等機械結(jié)構(gòu)中[1],以達(dá)到減振目的。含干摩擦結(jié)構(gòu)的模態(tài)特性,即模態(tài)頻率和由干摩擦現(xiàn)象引起的模態(tài)阻尼比,是結(jié)構(gòu)動力學(xué)設(shè)計工作中的重要關(guān)注點。然而,干摩擦導(dǎo)致的強非線性耗散特性,給含干摩擦結(jié)構(gòu)的模態(tài)特性預(yù)測和分析帶來了困難。

為了求解非線性模態(tài), ROSENBERG[2]提出非線性正則模態(tài)(nonlinear normal mode,NNM)的概念,將非線性模態(tài)定義為非線性無阻尼自治系統(tǒng)的同步周期振動。基于非線性正則模態(tài)的定義,衍生出多種解析計算方法,如多尺度法、正規(guī)形法等。然而這些方法各有不同的適用范圍,且計算效率低,很難應(yīng)用于實際復(fù)雜結(jié)構(gòu),因此需利用數(shù)值求解方法計算各種非線性結(jié)構(gòu)的非線性模態(tài)。基于非線性正則模態(tài)的定義,SLATER[3]通過Runge-Kutta 法,首次通過數(shù)值方法求解非線性模態(tài)。隨后,LEE等[4]通過打靶法,提出了更高效穩(wěn)定的非線性模態(tài)求解方法。

前人的研究主要針對保守系統(tǒng)的非線性模態(tài)。對于含干摩擦耗散特性的結(jié)構(gòu),其在初始擾動作用下的自由振動并不具備周期性特征。故而上述非線性正則模態(tài)的定義并不適用含干摩擦耗散因素的結(jié)構(gòu)。KRACK[5]通過人為引入負(fù)阻尼項用于補償由于干摩擦非線性所致的能量耗散,將非線性正則模態(tài)理論拓展應(yīng)用于非線性耗散系統(tǒng),由此形成了阻尼非線性模態(tài)(damped nonlinear normal mode, dNNM)的概念。基于非線性模態(tài)理論的發(fā)展,國外已經(jīng)開始著眼于基于非線性模態(tài)對結(jié)構(gòu)動力學(xué)分析與設(shè)計的應(yīng)用基礎(chǔ)研究,而國內(nèi)這方面的研究比較少見。

本文以含干摩擦梁結(jié)構(gòu)為例,基于阻尼非線性模態(tài)的定義,建立了含干摩擦耗散結(jié)構(gòu)的非線性模態(tài)高效數(shù)值分析方法體系,并提出了通過模態(tài)應(yīng)變能法對非線性模態(tài)阻尼比計算結(jié)果進(jìn)行驗證的技術(shù)途徑。

1 理論方法

本文以圖1所示含干摩擦單元的簡單梁元模型為研究對象(其中Ω為激振頻率),開展含干摩擦耗散特性結(jié)構(gòu)的非線性模態(tài)分析方法研究。該模型由7個梁單元構(gòu)成,干摩擦力由庫侖摩擦定律確定,如圖2所示。其主要參數(shù)見表1。

表1 模型參數(shù)

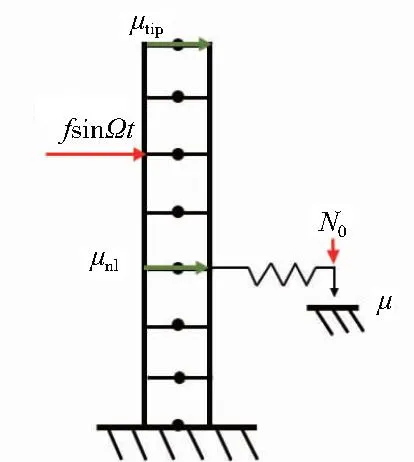
圖1 帶干摩擦單元的梁結(jié)構(gòu)

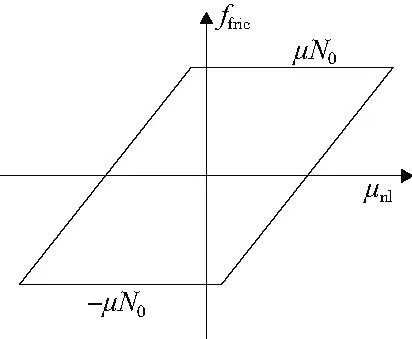
圖2 干摩擦力遲滯回線

1.1 含干摩擦非線性耗散系統(tǒng)的阻尼非線性模態(tài)

非線性模態(tài)(NNM)定義與線性系統(tǒng)類似。它被定義為非線性保守系統(tǒng)在不考慮外力和黏性阻尼力作用時,因受到初始擾動而產(chǎn)生的周期性自由振動。其動力學(xué)方程如下:

(1)

式中:M和K代表系統(tǒng)的質(zhì)量矩陣和剛度矩陣;u代表系統(tǒng)位移;t代表時間;fnl(u,t)代表不具有能量耗散性的非線性力,例如由于幾何非線性所致的彈性恢復(fù)力u3。

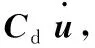
(2)

式中:Cd=-2ωζM,代表與質(zhì)量矩陣相關(guān)的負(fù)比例阻尼矩陣,其中ω和ζ分別代表非線性模態(tài)頻率與非線性模態(tài)阻尼比。

由此,針對含干摩擦非線性耗散系統(tǒng)的阻尼非線性模態(tài)(dNNMs)振動可定義為方程(2)所描述的非線性系統(tǒng)在初始擾動作用下的周期性自由振動。可以看出,基于此方法不僅可以計算得到系統(tǒng)的非線性模態(tài)頻率,還可以直接得到系統(tǒng)模態(tài)阻尼比的變化。通過模態(tài)阻尼比可以定量評估接觸非線性的阻尼能力,為其減振設(shè)計提供指引。

1.2 阻尼非線性模態(tài)仿真分析方法

為了更好地量化非線性耗散系統(tǒng)的能量相關(guān)性,通過引入新的參數(shù)模態(tài)幅值a,方程(2)的周期性位移響應(yīng)可以表示為u(t)=aΨ(t),將其展開為傅里葉級數(shù)形式:

(3)

式中:Nh表示截取的諧波階次;上標(biāo)c代表余弦項;上標(biāo)s代表正弦項。將式(3)中的傅里葉系數(shù)歸結(jié)為向量形式:

Ψ=[Ψ0,Ψc1,Ψs1,…,Ψck,Ψsk]

(4)

并定義系數(shù)轉(zhuǎn)換矩陣

T(t)=[I,cosωtI,sinωtI,…,coskωtI,sinkωtI]

(5)

式中I為Nd×Nd維單位矩陣,其中Nd為自由度數(shù)目。

位移解(式(3))可以改寫為

u(t)=aT(t)Ψ

(6)

引入頻域求導(dǎo)算子:

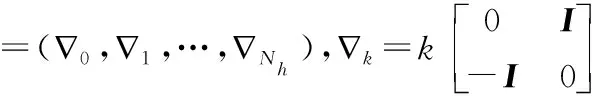
(7)

則系統(tǒng)的速度和加速度可以表示為

(8)

同理干摩擦力ffric(u,t)的傅里葉形式為

ffric(u,t)=T(t)·Ffric

(9)

式中Ffric為干摩擦力對應(yīng)的傅里葉系數(shù)向量,可通過時-頻域轉(zhuǎn)換技術(shù)獲取[6]。

將式(6)—式(9)代入式(2),并通過伽遼金法積分消去與時間項相關(guān)的T(t),得到由傅里葉系數(shù)向量表示的諧波平衡代數(shù)方程

P(ω,ζ)Ψ+Ffric(aΨ)=0

(10)

式中:P(ω,ζ)=a(ω2NM?2+ωNC?+NK);NC是分塊對角矩陣,NC=blkdiag(Cd,Cd,…),NM和NK的形式與NC相同。

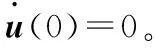
綜上,針對計算含干摩擦非線性耗散系統(tǒng)的阻尼非線性模態(tài)轉(zhuǎn)化為下列非線性代數(shù)方程的求解問題:

(11)

上述方程可通過牛頓拉夫遜法迭代求解。a起延拓參數(shù)的作用,可通過弧長延拓技術(shù)高效地追蹤獲取對應(yīng)其他模態(tài)振幅下的阻尼非線性模態(tài)振動。迭代求解過程中,可采用作者前期提出的雅可比矩陣快速計算方法[7],大幅提高上述非線性代數(shù)方程組的求解速度。

1.3 基于模態(tài)應(yīng)變能法的模態(tài)阻尼比計算

由于阻尼非線性模態(tài)的解可以作為穩(wěn)態(tài)受迫響應(yīng)被激發(fā),因此系統(tǒng)非線性模態(tài)阻尼比也可以從受迫響應(yīng)結(jié)果中得到。在一個完整振動周期內(nèi)的耗散能量Efric可以通過摩擦力對接觸界面上的相對位移的功計算。

(12)

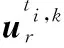
當(dāng)結(jié)構(gòu)最大振動幅值為A時,整個結(jié)構(gòu)的應(yīng)變能為

(13)

式中φj和ωr,j為第j階模態(tài)振型和固有頻率。

由于模態(tài)阻尼比常被定義為每弧度所耗散的能量與系統(tǒng)總能量的比值,即經(jīng)歷穩(wěn)態(tài)振動udNNM(Ωt)的非線性結(jié)構(gòu)的耗散能Efric與最大應(yīng)變能Ej的比值[8]。因此當(dāng)最大振動幅值為A時,模態(tài)阻尼比ζmse,j的計算如下:

(14)

第j階模態(tài)下整個結(jié)構(gòu)的模態(tài)應(yīng)變能Ej(aj)可以直接從ANSYS模態(tài)分析結(jié)果中獲取。因此,當(dāng)最大振動幅值為A、對應(yīng)的模態(tài)幅值為aj時,模態(tài)阻尼比ζmse,j(A)也可以由下式獲得:

(15)

通過式(14)或式(15)能夠評估由于摩擦非線性引起的非線性模態(tài)阻尼比ζmse,j,同時可以用于檢驗由阻尼非線性數(shù)值計算方法得到的非線性模態(tài)阻尼比ζj的準(zhǔn)確性。

2 結(jié)果和討論

2.1 非線性模態(tài)分析

將本文建立的非線性模態(tài)仿真計算方法應(yīng)用于圖1描述的梁模型,對其進(jìn)行阻尼非線性模態(tài)分析。對應(yīng)底層線性結(jié)構(gòu)第一彎曲模態(tài)梁尖端節(jié)點處的非線性模態(tài)特性如圖3和圖4所示。具有非線性模態(tài)頻率ω和位移幅值的單個dNNM表示為圖3中頻率-幅值曲線上的一個點,并繪制了單個dNNM中不同節(jié)點u(t)的周期運動。

圖3 非線性模態(tài)頻率

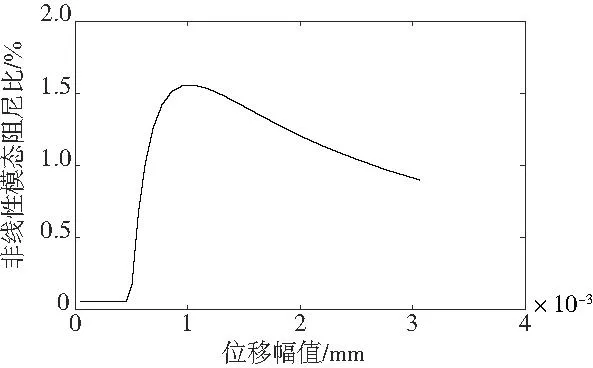
圖4 非線性模態(tài)阻尼比

由圖3和圖4可以看出,當(dāng)系統(tǒng)處于低幅值時,由于干摩擦單元保持黏滯狀態(tài),產(chǎn)生的摩擦力幾乎不影響結(jié)構(gòu)的模態(tài)特性。因此非線性模態(tài)頻率與非線性模態(tài)阻尼比處于線性階段,非線性模態(tài)阻尼比處于極低水平。隨著幅值的增加,干摩擦單元發(fā)生黏滑過渡現(xiàn)象,不斷增長的摩擦力導(dǎo)致頻率-幅值變化曲線出現(xiàn)剛度軟化特征。非線性模態(tài)頻率急劇下降并顯著提高系統(tǒng)的阻尼性能。需要注意的是,最大模態(tài)阻尼比是在中間幅值水平上產(chǎn)生的,最大約為1.5%,這意味著當(dāng)干摩擦單元處于部分滑動時獲得最大的摩擦阻尼性能。當(dāng)幅值持續(xù)增大,系統(tǒng)非線性模態(tài)頻率趨于收斂,非線性模態(tài)阻尼比逐漸回落。

2.2 非線性模態(tài)與強迫振動響應(yīng)之間的關(guān)聯(lián)

系統(tǒng)的骨架曲線能夠描述非線性系統(tǒng)的頻率-能量相關(guān)性。骨架曲線是系統(tǒng)在不同激振力作用下,不同幅頻曲線的響應(yīng)峰值相連得到的曲線。圖5描述了系統(tǒng)在不同激振力下(fi+1>fi,i=1,…,3)的幅頻特性曲線。

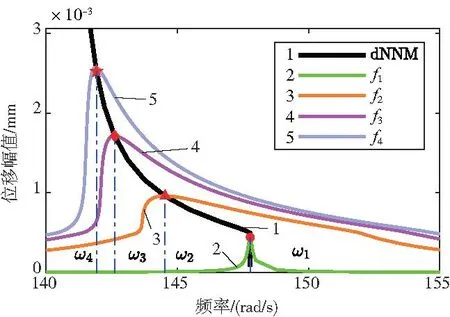
圖5 不同激振力下的幅頻曲線

由圖5觀察到非線性模態(tài)數(shù)值計算方法得到的系統(tǒng)幅值-頻率曲線即為骨架線。通過非線性模態(tài)幅值-頻率曲線可以準(zhǔn)確預(yù)測系統(tǒng)在不同水平激振力作用下響應(yīng)峰值的變化軌跡,避免了繁瑣耗時的強迫響應(yīng)計算。

2.3 非線性模態(tài)阻尼比的檢驗

在強迫振動響應(yīng)的基礎(chǔ)上,根據(jù)1.3節(jié)介紹的模態(tài)應(yīng)變能方法,即式(15)得到非線性模態(tài)阻尼比ζmse(用MSE表示)與位移幅值的變化關(guān)系,可以用來評估非線性系統(tǒng)的非線性模態(tài)阻尼比ζmse,同時可以用來檢驗阻尼非線性模態(tài)(dNNM)計算得到的模態(tài)阻尼比ζ。圖6描述了分別通過模態(tài)應(yīng)變能法和阻尼非線性模態(tài)計算方法得到的模態(tài)阻尼比與位移幅值的變化關(guān)系。由圖6觀察到,ζ和ζmse之間存在良好一致性。因此,充分證明了本文所建立的阻尼非線性模態(tài)分析方法在評估干摩擦阻尼能力方面的有效性。

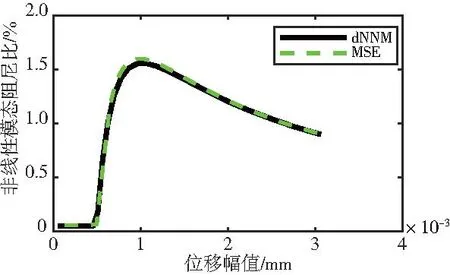
圖6 不同方法下的模態(tài)阻尼比變化

3 結(jié)語

本文基于阻尼非線性模態(tài)理論,綜合采用多諧波平衡法、雅克比矩陣快速計算方法等先進(jìn)數(shù)值仿真技術(shù),建立了干摩擦耗散特性結(jié)構(gòu)的非線性模態(tài)高效仿真分析方法,為擴展到實際工程結(jié)構(gòu)奠定基礎(chǔ),具有很好的應(yīng)用價值。主要結(jié)論如下:

1)實現(xiàn)了含干摩擦梁結(jié)構(gòu)的非線性模態(tài)分析,揭示其非線性模態(tài)頻率與非線性模態(tài)阻尼比隨振幅增長的變化規(guī)律,并將非線性模態(tài)與強迫振動響應(yīng)聯(lián)系,驗證了系統(tǒng)在共振區(qū)域的響應(yīng)可以通過非線性模態(tài)近似,避免了強迫振動響應(yīng)的計算;

2)提出了通過模態(tài)應(yīng)變能法對非線性模態(tài)阻尼比計算結(jié)果進(jìn)行驗證的技術(shù)途徑,進(jìn)而驗證了本文建立的非線性模態(tài)數(shù)值仿真計算方法可以有效評估系統(tǒng)的阻尼能力,為后期干摩擦裝置的設(shè)計和優(yōu)化提供指導(dǎo)。