抗菱剛度對平車性能的影響研究

張博寧,王勇,張勝建,呂小勇

(西南交通大學 牽引動力國家重點實驗室,四川 成都 610031)

0 引言

鐵路貨物運輸是運輸的主要方式之一,它在整個運輸領域中占有重要的地位并發揮著重要的作用。找出影響車輛性能的關鍵因素,對改進貨車的性能有著重要的作用,其中抗菱剛度就是貨車的動力學性能指標重要影響因素之一。

國內學者對貨車抗菱剛度進行了大量的研究。王金棟等[1]研究推導了貨車轉向架斜楔減振器抗菱剛度計算方法。劉嘉興等[2]通過Abaqus有限元軟件和Simpack動力學軟件進行仿真計算對變摩擦轉向架斜楔等效剛度的計算進行了推導和應用。羅林濤等[3]指出交叉支撐裝置可以提高高速轉向架的抗菱剛度 。任利惠等[4]對貨車轉向架抗菱剛度的測量方法進行了研究并提出了直接和間接兩種測量方法。宋子洋等[5]研究鐵路貨車頂置式斜楔軸箱懸掛結構中斜楔摩擦角對三軸轉向架動力學性能的影響。

前人關于抗菱剛度對貨車動力學性能影響的研究較少,因此本文在前人的基礎上,通過Simpack動力學軟件建立出口的某型平車動力學模型,對不同抗菱剛度下的空車新輪、空車磨耗輪、重車新輪、重車磨耗輪的動力學性能分別進行仿真計算,研究抗菱剛度對其蛇行運動臨界速度、運行平穩性、運行穩定性的影響規律。

1 整車非線性動力學模型

利用Simpack仿真軟件對車輛系統進行建模和求解。

平車整車系統由1個車體和2個轉向架組成,每個轉向架又由2個輪對、4個軸箱、4個斜楔和構架組成。本模型采用傳統的三大件式轉向架,因此每個構架包括2個側架和1個中央搖枕,共計27個剛體。各剛體的自由度數如表1所示。車體考慮6個自由度,即縱向、橫向、垂向、側滾、點頭、搖頭;側架考慮6個自由度,即縱向、橫向、垂向、側滾、搖頭、點頭;搖枕考慮3 個自由度,即垂向、側滾、搖頭;斜楔考慮3個自由度,即縱向、橫向、垂向,同時引入3個約束;輪對考慮6個自由度,即縱向、橫向、垂向、側滾、點頭、搖頭;軸箱考慮1個自由度,即點頭;再考慮到鋼軌的橫向位移、垂向位移以及縱向的扭轉,整個車輛系統共計80個自由度。

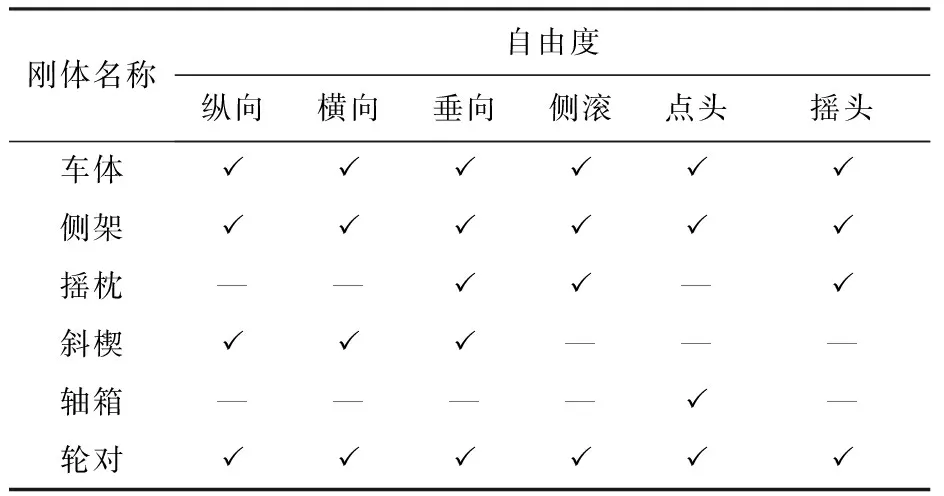
表1 車輛系統模型自由度

平車模型是一個繁瑣的多體系統模型,部件與部件之間既存在相互作用力又有相對運動,除此以外,輪軌之間也存在相互作用。為了達到理論計算分析模型研究的主要目的,必須對一些次要因素進行相應的假定或簡化。在建立出口的某型平車系統模型時做出如下假定:輪對、側架、搖枕、車體和軸箱等部件的彈性比懸掛系統的彈性要小得多,均視為剛體,即忽略各部件的彈性變形;不考慮平車牽引工況和相鄰車的影響,只考慮單車模型;車體、轉向架各部件及懸掛均對稱布置。

建立的Simpack剛體非線性動力學模型如圖1所示。

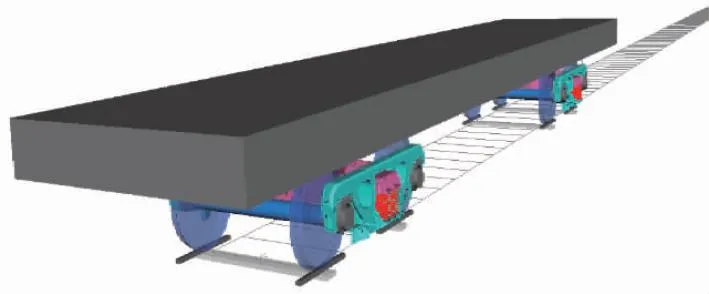
圖1 平車Simpack模型

非線性輪軌接觸幾何關系采用P8踏面車輪和UIC54鋼軌相匹配的輪軌接觸幾何關系。新輪和UIC54匹配的名義等效錐度為0.12,磨耗輪和UIC54匹配的名義等效錐度為0.3,輪軌接觸點在車輪和鋼軌上分布均勻。其中新輪的輪軌接觸幾何關系如圖2所示。

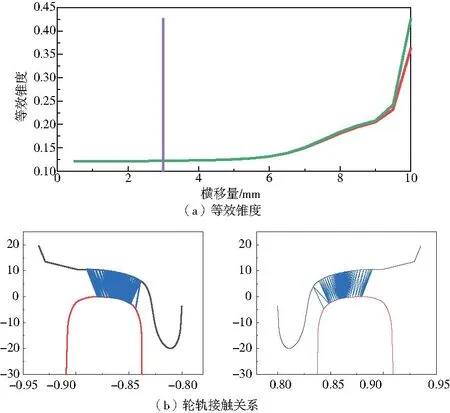
圖2 輪軌接觸幾何關系

2 抗菱剛度

抗菱剛度定義為兩側架因速度差導致出現前后錯動情況而使轉向架出現菱形變形,提供抵抗這種菱形變形的剛度即為抗菱剛度[2]。

本平車模型采用三大件式轉向架,主要由中央搖枕和側架組成,搖枕與側架之間通過7組螺旋鋼彈簧連接,每側側架與搖枕之間還設有兩個斜楔,通過減振簧和側架連接。傳統三大件式轉向架具有結構簡單、均載性好、對線路適應性強、易于檢修等優點,但是傳統的三大件式結構也帶來了抗菱剛度不足、蛇行失穩臨界速度低的缺點[3]。三大件貨車轉向架抗菱剛度主要由搖枕彈簧、斜楔減振系統、軸箱彈性墊以及提高抗菱剛度裝置4 個部分提供[5]。而本模型的抗菱剛度主要由變摩擦斜楔減振器提供。文獻[1-2]中對抗菱剛度由變摩擦斜楔減振器提供的計算公式均有推導。根據文獻[1]可知變摩擦斜楔減振器提供的抗菱剛度為

(1)

式中:b為斜楔寬度;kx表示斜楔彈簧剛度;ky表示搖枕彈簧剛度;α為副摩擦面與水平面間的夾角。

原車設計的空車抗菱剛度為2.5MN·m/rad,重車的抗菱剛度為7MN·m/rad。

3 仿真計算結果分析

3.1 抗菱剛度對蛇行運動臨界速度的影響

蛇行運動穩定性是軌道車輛最重要的性能指標之一,通過動力學仿真計算蛇行運動臨界速度最常用的方法有降速法和極限環法。

本模型采用極限環法獲取臨界速度,即當模型在沒有任何激擾的理想情況下運行一段距離后給軌道加激勵,然后再恢復初始的理想狀態,車輛系統首次出現不能回到平衡位置的情況,此時的速度即為臨界速度。添加激勵有很多種方法,例如實測的軌道激勵樣本、車輛某些結構的初始位移或速度、隨機的初始狀態都可以作為添加的激勵。考慮到出口國鐵路線路較差,本模型采用美國4級譜作為軌道激勵,分別計算了空車新輪、空車磨耗輪、重車新輪、重車磨耗輪4種工況下不同抗菱剛度的蛇行運動臨界速度(圖3)。

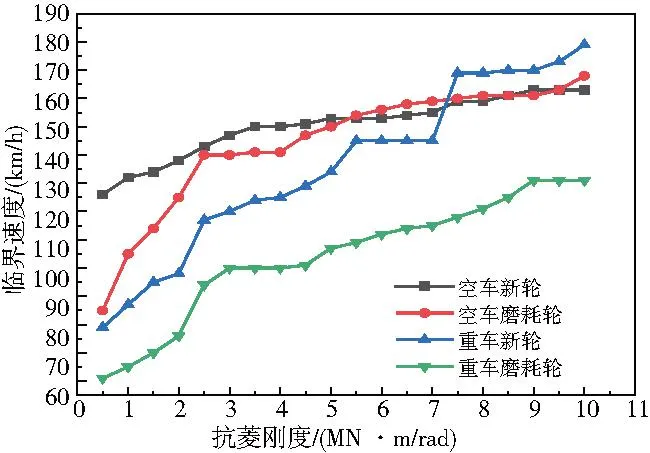
圖3 臨界速度

根據圖3可以看出,抗菱剛度對空車新輪的影響最小,對重車新輪的影響最大。

隨著抗菱剛度的增加,空車新輪的臨界速度緩慢增加。當抗菱剛度大于3MN·m/rad時,隨著抗菱剛度的增加臨界速度趨于穩定。對于其他3種工況,隨著抗菱剛度的增加,臨界速度整體上呈現出階梯狀增長;當抗菱剛度小于3MN·m/rad時,隨著抗菱剛度的增加,臨界速度快速升高;當抗菱剛度大于3MN·m/rad時,空車磨耗輪和重車磨耗輪的臨界速度升高速度減緩,重車新輪的臨界速度升高速度依然較快;當抗菱剛度大于7MN·m/rad后,重車新輪的臨界速度增長幅度較大后趨于穩定。

3.2 抗菱剛度對平穩性的影響

我國現行鐵路軌道車輛的評價標準主要依據GB/T5599—2019[6],其中用于評價平穩性的部分絕大多數是基于Sperling平穩性指標發展而來。

平穩性指標計算公式為[7]

(2)

式中:A為振動加速度;f為振動頻率;F(f)為頻率修正系數。

貨車的平穩性評定標準見表2[7]。

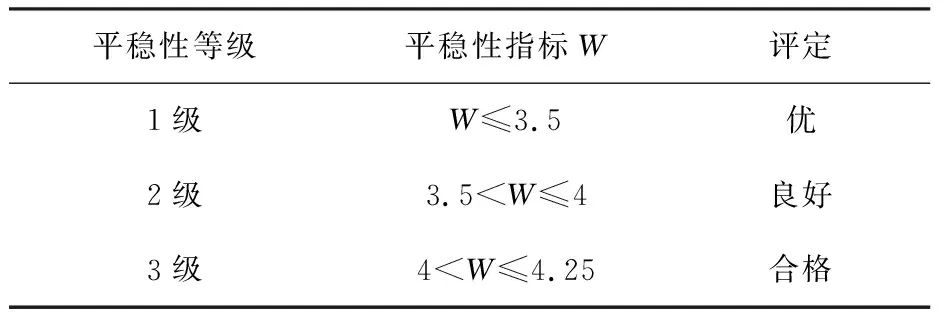
表2 平穩性指標等級表

本模型以出口的某型平車作為分析對象,該車的設計速度為100km/h,因此,本模型對4種工況均以100km/h的速度在加有美國4級譜的軌道上進行仿真,對測得的平穩性數據進行分析。

圖4—圖5所示分別為空車橫向、垂向平衡性。從圖4和圖5可以看出,抗菱剛度對空車新輪的橫向和垂向平穩性均沒有什么影響。當抗菱剛度過低小于1.5 MN·m/rad時,空車新輪和磨耗輪的平穩性都非常差,磨耗輪的橫向平穩性已經不能達到合格的標準;當抗菱剛度大于1.5 MN·m/rad,空車橫向平穩性隨著抗菱剛度的增大緩慢減小最后趨于穩定;空車垂向平穩性幾乎不受抗菱剛度的影響。

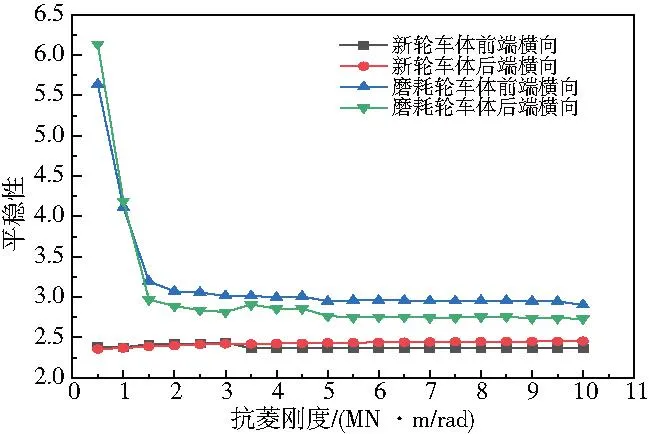
圖4 空車橫向平穩性

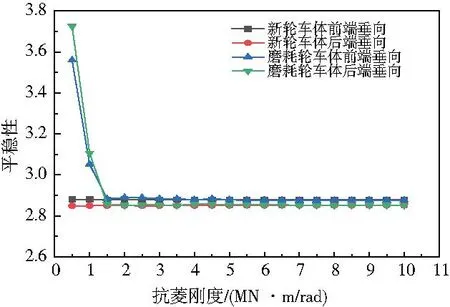
圖5 空車垂向平穩性

圖6—圖7所示分別為重車垂向、橫向平穩性。從圖6和圖7可以看出,當抗菱剛度小于3 MN·m/rad時,抗菱剛度對重車后端垂向平穩性影響較小,重車其他橫向和垂向平穩性都較差,且對橫向平穩性的影響更大,抗菱剛度從2 MN·m/rad增到3 MN·m/rad這一過程中,重車平穩性指標大幅度降低,重車的平穩性大幅提高;當抗菱剛度大于3 MN·m/rad后,磨耗輪橫向平穩性隨著抗菱剛度的增加逐漸減小,重車新輪橫向平穩性和重車垂向平穩性幾乎不再受抗菱剛度的影響。

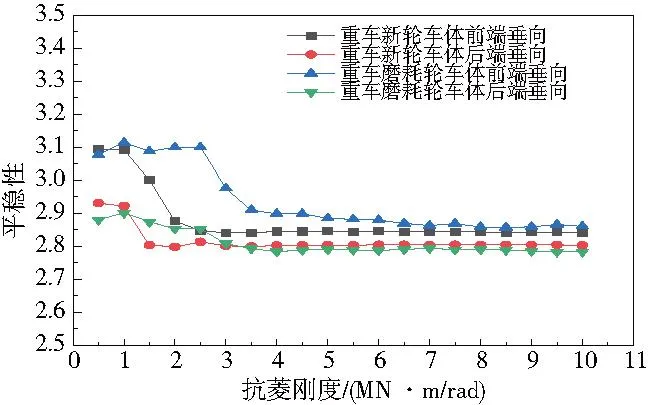
圖6 重車垂向平穩性

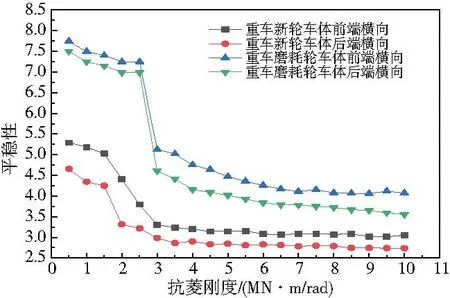
圖7 重車橫向平穩性

3.3 抗菱剛度對運行穩定性的影響

運行穩定性主要是通過對輪重減載率,脫軌系數,輪軸橫向力3項指標進行評定。GB/T5599—2019中3項指標的規定如下[6]:貨車在通過小曲線半徑(250m～400m)時脫軌系數應小于等于1.2;在試驗速度小于160km/h的情況下,輪重減載率應不高于0.65;輪軸橫向力的計算公式為H≤15+(P0/3),式中的P0為靜軸質量。

貨車在通過曲線時最容易發生脫軌,因此本模型在進行運動安全性仿真時選取半徑R350m 、超高h100mm、緩和曲線110m的小半徑曲線進行仿真,通過速度設為60km/h,曲線全程加載美國4級譜。為了更直觀地觀察抗菱剛度對這些指標的影響趨勢,對輪重減載率、脫軌系數、輪軸橫向力3項指標進行歸一化處理并進行分析,如圖8—圖10所示。

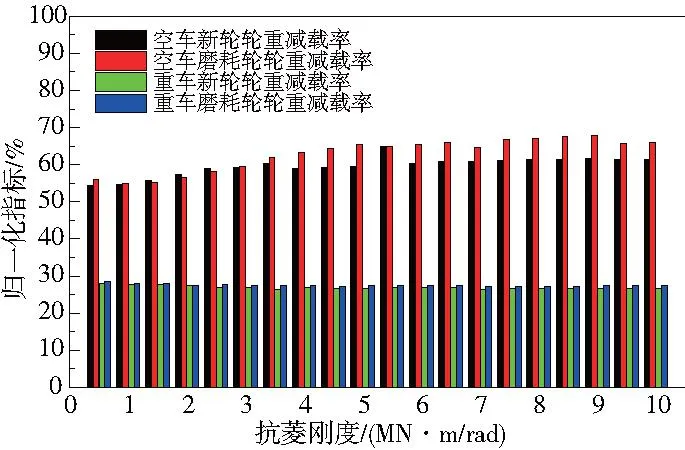
圖8 輪重減載率

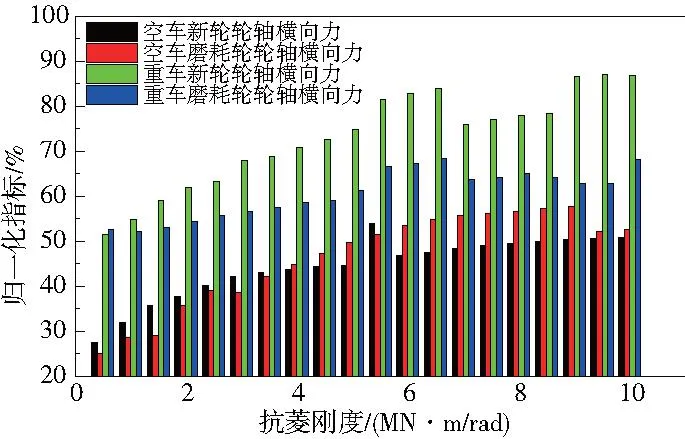
圖9 輪軸橫向力

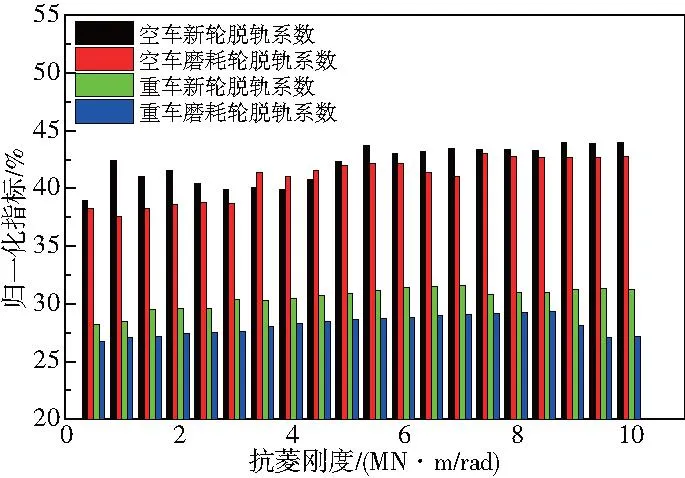
圖10 脫軌系數

從圖8—圖10可以看出:

1)抗菱剛度對重車的輪重減載率影響很小,隨著抗菱剛度的增大,重車的輪重減載率指標緩慢減小后趨于穩定;空車輪重減載率指標小幅增加后趨于穩定。

2)隨著抗菱剛度的增加,空車和重車的輪軸橫向力指標均出現明顯的增大,其中對新輪的影響最為明顯。當抗菱剛度過大時,輪軸橫向力指標有超標的風險。

3)抗菱剛度對脫軌系數指標的影響較小,隨著抗菱剛度增大,脫軌系數指標先小幅升高,之后趨于穩定。

3.4 規律驗證

為了驗證規律的正確性,本小節分別取空車磨耗輪抗菱剛度分別為1.0MN·m/rad和2.5MN·m/rad兩種工況和重車新輪抗菱剛度分別為5.5MN·m/rad和6.5MN·m/rad兩種工況,速度取80km/h,在直線工況下對上述規律進行驗證,驗證結果如表3所示。

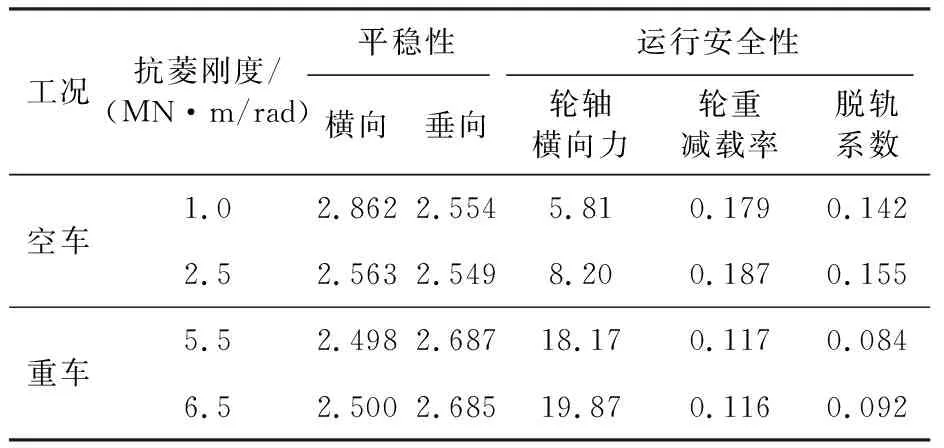
表3 車輛動力學指標

從表3可以看出,在選取不同速度級時各指標的變化規律相同,從而驗證了該規律的正確性。

4 結語

本文以出口的某型平車作為研究對象,通過Simpack動力學軟件建立平車模型,以抗菱剛度作為變量對模型進行動力學仿真,對結果進行分析后得出以下結論。

1)抗菱剛度對空車新輪的臨界速度影響較小,其他3種情況的臨界速度總體上呈現出階梯狀的增長,其中對重車新輪臨界速度的影響最大。在合理范圍內應盡可能選擇較大的抗菱剛度。

2)總體看,抗菱剛度對平穩性指標的影響較小,僅當抗菱剛度低于1.5 MN·m/rad時,磨耗輪的平穩性較差,尤其是空車磨耗輪的橫向平穩性。

3)抗菱剛度對輪重減載率指標和脫軌系數指標的影響很小;抗菱剛度對輪軸橫向力指標有很大的影響,當抗菱剛度過大時,輪軸橫向力指標有超標的風險。

4)大的抗菱剛度雖然有利于蛇行運動臨界速度的提升,但過大的抗菱剛度也大大增大了車輛脫軌的風險,因此抗菱剛度不易選擇過大。