柔性作業車間差分退火調度優化算法研究

覃 斌,宋文廣,張秋娟,尹 強,高子召, Yu Qian

(長江大學 計算機科學學院,湖北 荊州 434023)

在科技與制造行業急速發展的現今,各企業的生產制造流程也在不斷優化。生產調度問題長期以來一直是制造系統的熱門問題,其理論研究也是最為艱難跨越的障礙之一。調度的任務是由生產目標和約束,來為工件明確合適的加工時間、路線、器械和順序等[1]。該研究不僅能改善效率,提高企業競爭力,同時還能降低能耗,實現制造業的綠色發展。柔性作業車間調度問題(flexible job-shop scheduling problem,FJSP)作為傳統車間調度的擴展,更加符合實際生產中的制造環境,增強了生產調度的靈活性。同時FJSP比傳統作業車間調度問題更為復雜,不僅需要對工序加工的順序進行排序,還要給工序分配機器,因此被歸為NP-hard類問題[2]。

雖然FJSP的復雜性眾所皆知,但是為了適應發展趨勢,許多學者還是致力于FJSP的研究。張凱等[3]構建了一種將柔性作業車間調度問題轉化為馬爾可夫決策過程的方式,并提出集成5種DQN優化的算法D5QN求解FJSP;張博等[4]提高了粒子群算法在求解FJSP中獲取最優解的速度;Escamilla等[5]提出了一種新的元啟發式算法(global-local neighborhood search algorithm,GLNSA),同時結合禁忌搜索算法(tabu search, TS),完成了對FJSP的優化;Danial[6]等提出了一種高效的兩階段遺傳算法(2SGA)求解FJSP,效率相對傳統遺傳算法有很大的提升;王玉芳等[7]以優化最大完工時間為目標,提出一種自適應灰狼優化算法(adaptive grey wolf optimization, AGWO)求解該問題。

差分進化算法(differential evolution algorithm,DE)是一種快捷有效的智能優化算法[8],它基于群體差異的啟發式隨機搜索,受控參數少、魯棒性強,具有較強的全局收斂能力和穩健性。但是差分進化算法在柔性作業車間問題中,尋優的速度較慢,而且比較容易陷入局部最優解中[9],因此本文提出了一種改進的差分進化算法(improved differential evolution-simulated annealing algorithm,IDESA)來求解FJSP,此算法在改進的差分進化算法的基礎上,加入模擬退火操作以提高算法的尋優能力。

1 FJSP模型設計

1.1 FJSP的描述

FJSP是指在一個生產系統中,有一個機器集合,該集合中有m臺可以用來加工的機器。這個機器集合可表示為M=(M1,M2,...Mm)。同時有一個由需要加工的工件所組成的工件集J=(J1,J2,...Jn),其中的每一個工件要經歷p道加工程序,將這些加工程序記為P=(P1,P2,...,Pn),其中每道程序都將會在M中的一臺或多臺機器上進行加工,不同機器的選擇將致使加工需花費的時間不盡相同。FJSP需要解決的問題就是通過調度方法選擇最優的一條加工順序,及每道工序加工的設備,在滿足約束條件的情況下達到最好的生產效益。表1是一個FJSP示例。

表1 4×4完全柔性作業車間調度示例

1.2 FJSP的符號表示

在FJSP中,各個實體及操作等將會采用統一的符號進行表示,下文中所涉及的符號如表2所示。

表2 統一符號表示

1.3 FJSP的約束條件

FJSP中一系列的條件約束將最終的結果導向實際環境中我們想要達到的優化效果。本文將以經典的最大完工時間最小化問題來建立約束條件。

sjk+Pijk×tijk≤eij

(1)

ejk≤sj(k+1)

(2)

公式(1)和公式(2)表示在工件加工的過程中,必須按照固定的工件加工順序來進行,前一個工序未執行之前不允許跳過此工序加工下一個工序。

Ej≤Emax

(3)

公式(3)約束了每一個工件加工的完成時間,不能超過所有工件完成以后總的完工時間。

sjk+tijk≤sln+H(1-Qjklni)

(4)

ejk≤sj(k+1)+H(1-Qlnj(k+1)i)

(5)

公式(4)和公式(5)表示在相同的時間點,一個機器只能加工某一個工件的一道工序,此時此工件獨占此臺機器。

(6)

公式(6)約束了在相同的時間點上,同一道工序只能被一臺機器加工。同時需要保證sjk,ejk的取值必須大于等于0。

不同的生產環境優化目標也有所不同,當前已有眾多學者針對不同優化目標做出了研究,如趙詩奎等[10]研究基于極限調度完工時間(Climit)最小化的機器選擇方式,陳廣鋒等[11]選擇全局最小負荷為目標求解FJSP。由于本文的目標是對加工時間進行縮減,所以目標函數是在最大完工時間的基礎上使其最小化:

minEmax=min{max{maxEi}}

(7)

2 差分進化算法的優化

2.1 差分進化算法改進

本文將在差分進化算法中加入模擬退火操作。模擬退火算法有著較強局部極值逃脫能力和不依賴初值的特點,但整體搜索能力較弱;而差分進化算法作為隨機的啟發式搜索算法,全局尋優的能力更具優勢。

2.2 算法優化流程

2.2.1 編碼方式

單一的編碼方式很難獲取最優解[12],因為FJSP在給加工工序排序的同時還要給工序分配可加工機器,問題的可行解需要確定工序先后順序的編碼和給工序分配機器的編碼兩部分,因此采用雙層編碼,如圖1所示。

圖1 編碼方式

以表1為例,假如工序O11、O12、O13、O21、O22、O23、O31、O32、O41、O42的加工順序為O23-O32-O13-O21-O12-O42-O41-O11-O31-O22,那么工序編碼為[2,3,1,2,1,4,4,1,3,2]T;假如工序O11、O12、O13、O21、O22、O23、O31、O32、O41、O42對應的加工機器為M2、M4、M2、M1、M3、M2、M4、M1、M1、M3,那么機器編碼則為[2,4,2,1,3,2,4,1,1,3]T。每個工件的工序數目是確定的,而工序編碼只是負責記錄工件的加工順序,因此編碼具有唯一性。

2.2.2 種群初始化

初始種群的質量直接影響算法的收斂速度和性能,初始種群質量越好,DE算法的效果越顯著。在大部分DE算法中,初始化種群一般會采取完全隨機的初始化方式,該方式雖然能夠較好的實現了隨機性和多樣性,但是得到的初始解質量大多都偏低,可能需要進化更多的代數才能計算出理想解。

本文對工序碼采取隨機生成的初始化方式,而對機器碼則使用輪盤賭的初始化策略。初始化策略如下:

步驟1 首先,隨機生成工序碼。

步驟2 對于生成碼中的每道工序,取出能對其處理的機器集。

步驟3 將相應機器上各工序加工的時間,取倒數,累加得到總概率。

步驟4 計算每臺機器的時間占總時間的概率,作為被選擇的概率。

步驟5 每道工序對應的各機器的被選擇概率隨機生成該工序加工機器的機器號。

通過這種方式可以得出,機器加工工序的時間越長,則其被選中的概率越小,反之,其被選中的概率就越大。這樣不僅保證了隨機性和多樣性,也提高了初始種群的質量,為之后的進化步驟提高了效率和準確率。

2.2.3 變異

(8)

2.2.4 交叉

(9)

式中:Cr表示交叉概率,p是在區間[1,D]上的隨機整數。

2.3.5 模擬退火操作

在經過變異、交叉操作之后不再進行差分進化算法的選擇過程,而是通過模擬退火算法Metropolis[13]準則進行選擇,判斷是否接受實驗向量,然后再繼續模擬退火的降溫操作,依次往返執行到模擬退火規則下的終止條件,輸出結果。求解步驟如下:

1)設置開始溫度Ts和結束溫度Te。

2)當溫度參數T=T0時,在可行解的空間內生成一個新解,新解產生公式為:

Xnew=Xold?Random

(10)

式中:Xnew為新解,Xold為執行交叉變異后的個體,Random為一個隨機的擾動向量。

3)計算新解的適應度f(Xnew),以及新解和原始解之間的適應度差值ΔE=f(Xnew)-f(Xold),然后以概率p=exp(-ΔE/T)確定是否選擇該新個體進入下一代,最后執行退溫操作。重復上述過程到滿足條件后產生下一代種群個體。

IDESA算法完整流程如圖2所示:

圖2 IDESA算法流程

3 實驗

本節實驗在Windows11 64bit的個人筆記本電腦上運行,CPU為Intel(R) Core(TM) i9-12900 H、內存為16 GB。

為了測試算法在柔性作業車間調度問題求解中的性能,選取Brandimarte[14]給出的10組柔性作業車間調度算例(mk01～mk10),這些算例通常被用來測試算法的性能。本次實驗的種群規模設置為50,最大進化代數設置為500。通過測試將變異概率和交叉概率設置為0.1,模擬退火操作的初始溫度為100 ℃,終止溫度為1 ℃,以Tk=0.9Tk+1執行降溫操作。與比較的算法各自獨立運行10次,與本文算法相比較。各算法的最優解如表3所示。

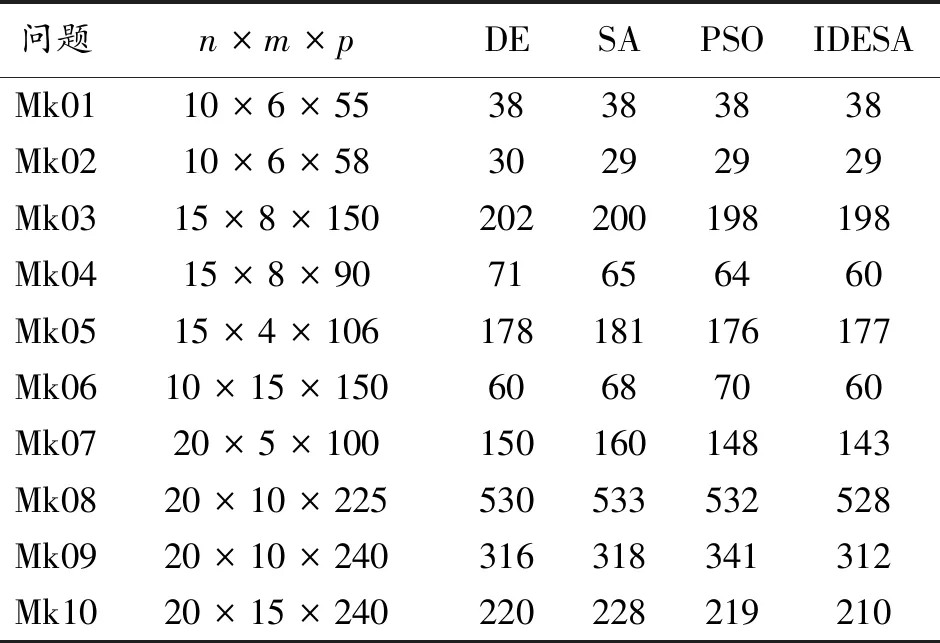
表3 Brandimarte算例測試結果對比

式中:n表示工件數,m表示機器數,p表示工序數,將本文算法分別與差分進化算法(DE)、模擬退火算法(SA)和粒子群算法(PSO)進行對比。可以看出,本文算法結合了差分進化算法和模擬退火算法的優勢,隨著問題規模的增大,尋優能力明顯優于其他三種算法。圖3給出了四種算法在Mk02問題中最優解的收斂情況。

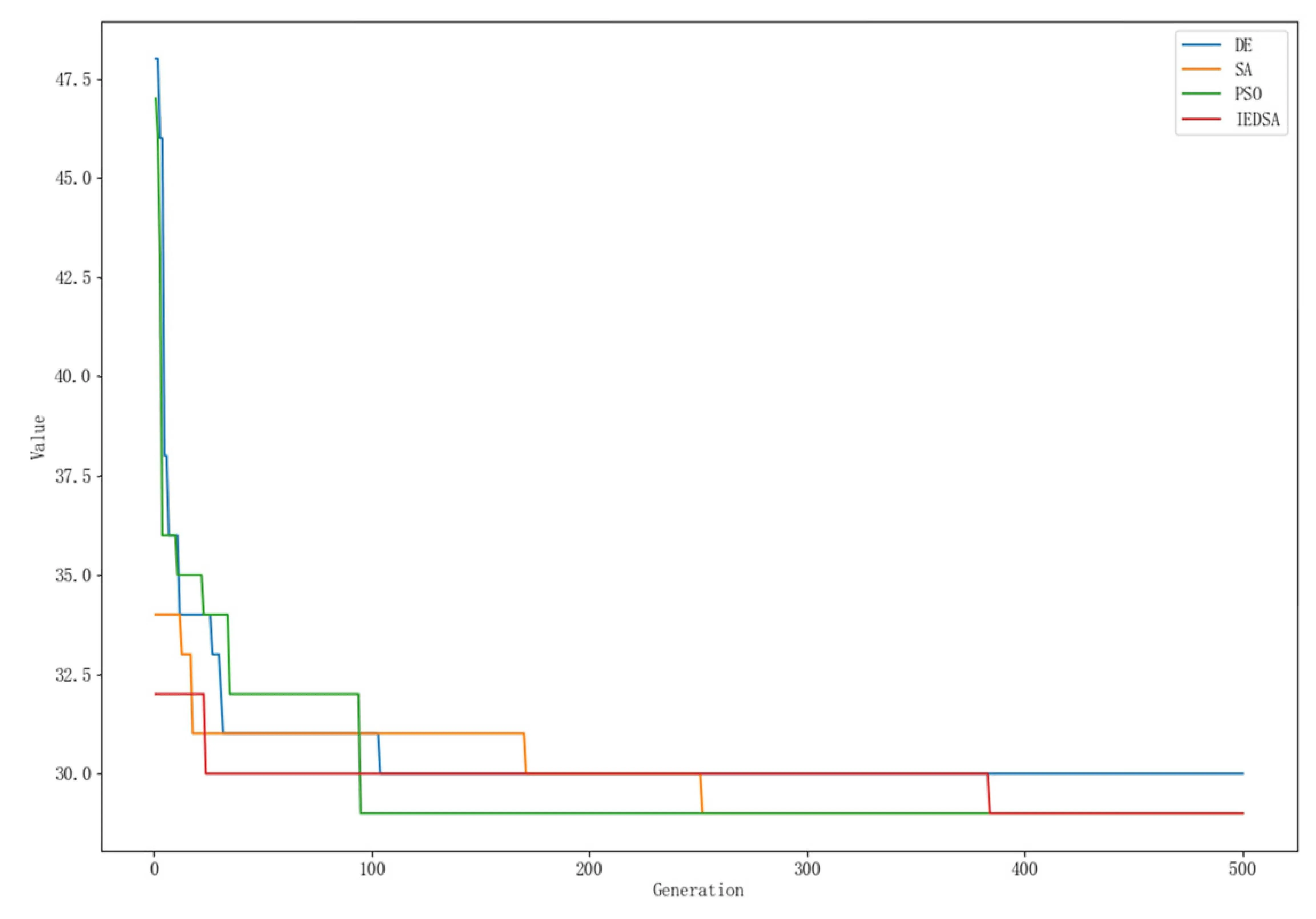
圖3 Mk02問題全局最優解收斂圖

由圖3可以看出,IDESA算法中新的種群初始化方式大大提高了初始解的質量,同時在加入模擬退火操作后,種群迭代到380代左右時,并沒有像傳統的差分進化算法一樣陷入局部極值,而是能夠跳出局部最優解,尋優能力明顯提高。圖4給出了Mk02問題的最優調度甘特圖。

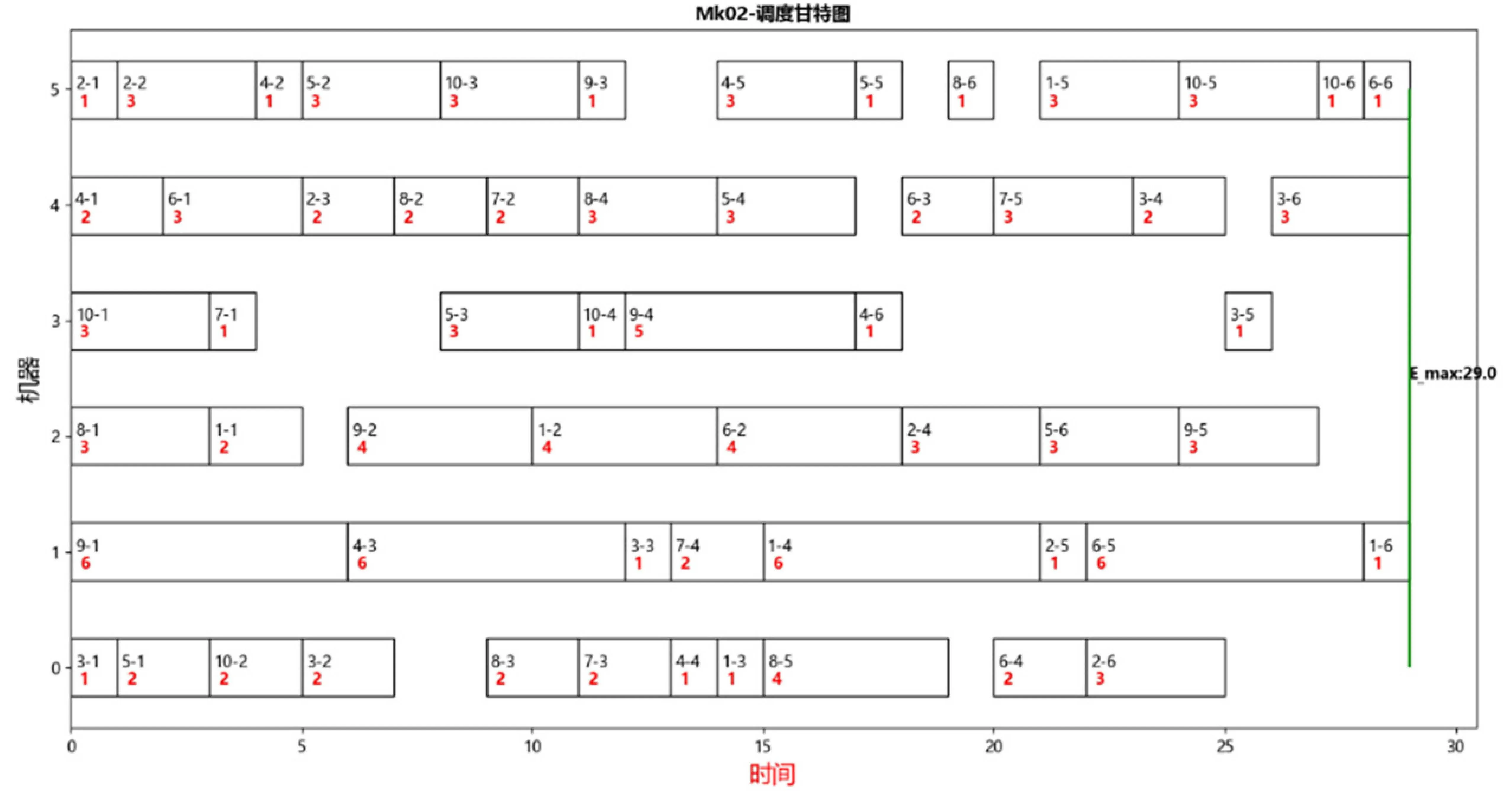
圖4 Mk02問題最優甘特圖

通過實驗可得出,IDESA算法能夠提升求解速度,又不會陷入局部最優。針對在處理柔性作業車間調度的問題上,調度效率提升的同時,也保證了分配結果的最優性。

4 結束語

本文設計出一種改進的差分算法并結合模擬退火算法解決柔性作業車間調度問題。通過特殊的雙層編碼方式,以及種群初始化方式和DE/best/1變異方式,提高了差分進化算法的全局搜索能力,同時在算法的選擇階段中與退火操作結合,彌補了DE算法局部搜索的缺陷。最后使用Brandimarte標準算例進行了驗證,FJSP中的最大完工時間得到有效縮短,且保證了調度分配質量,證實了本文算法的優勢與可行性。

本文驗證了以最小化最大完工時間作為優化目標的結果,在實際生產制造中,還需要考慮運輸時間、機器損耗、加急工件等各種情況,因此后續將繼續研究多目標、高緯度情況下的FJSP。