受外壓含缺陷夾層管非線性屈曲分析

摘要：為了研究外壓作用下夾層管非線性屈曲問題，使用有限元軟件ANSYS建立夾層管模型，通過線性屈曲分析獲得的屈曲模態制作非線性屈曲的初始缺陷，對受到外壓的夾層管進行非線性屈曲分析。研究表明：含有模態缺陷的夾層管在受外壓屈曲過程中，會在管徑方向產生變形，包括壓縮變形和膨脹變形，變形沿軸向傳播，壓縮變形量始終大于膨脹變形量;使用拐點法，即二者的比值來判定夾層管是否失穩，此方法可以精準判斷夾層管失穩外壓值，對初始缺陷相同，壁厚比不同的內外管和夾芯層失穩外壓進行了分析。研究成果可為夾層管的應用提供借鑒。

關鍵詞：夾層管;非線性屈曲;失穩壓力;壓縮變形;膨脹變形

中圖分類號：TE931.2" " " " "文獻標志碼：A" " " "doi：10.3969/j.issn.1001-3482.2024.04.004

Nonlinear Buckling Analysis of Defected Sandwich Tubes under External Pressure

BIAN Yekai，GENG Dai， ZHANG Qiang，WANG Wenqiang，WANG Yanlong

（School of Mechanical Science and Engineering，Northeast Petroleum University，Daqing 163318，China）

Abstract： In order to study the nonlinear buckling problem of the sandwich tube under external pressure，the finite element software ANSYS was used to establish a model of the sandwich tube，and the initial defects of nonlinear buckling were generated by the buckling modes obtained from the linear buckling analysis，and the nonlinear buckling analysis was carried out on the sandwich tube under external pressure. It is found that in the process of buckling under external pressure，the laminated pipe containing modal defects produces deformation in the direction of pipe diameter，including compression deformation and expansion deformation，and the deformation propagates along the axial direction，and the amount of compression deformation is always larger than the amount of expansion deformation. With the inflection point method，that is，the ratio of the two to determine whether the sandwich tube is unstable or not，this method can accurately determine the value of external pressure of the sandwich tube instability. In addition，this inflection point method can be used to analyze the destabilized external pressure of internal and external pipes and sandwich layers with the same initial defects and different thickness-to-diameter ratios. The research results can provide reference for the application of sandwich tubes.

Key words： sandwich tube;nonlinear buckling;buckling pressure;compression deformation;expansion deformation

為了滿足當今世界油氣使用需求，對油氣的探索已經向著更深的海底進發。海底管道作為運輸油氣的主要工具，有運輸量大、運輸速度快、運輸距離遠等優點，它一般為單層管，常規的單層管需要承受外壓、浮力和低溫的挑戰，因此只能應用于一定的水深。為了彌補單層管的這些不足，夾層管應運而生[1]。夾層管一般為長圓柱形結構，由三層組成，內層與外層是相同材料的鋼管，內管用來承受管內油氣的侵蝕，外管用來抵抗外部水流的壓力，中間夾芯層為聚丙烯材料，具有很強的保溫隔熱功能，管內各層完全粘結，這可保證承受更大的壓力。夾層管的內中外三層共同工作，使管道兼具保溫性能和抗壓能力，這在深水當中，認為是最合適的設計配置，特別是在超深水中應用[2]。

針對海底管道失穩屈曲問題的研究，對于單層管方面起步較早并已經做了相當多的研究，而復合海底管道領域起步較晚且研究較少。Kardomates等[3]采用數值分析方法，研究了外壓作用下夾層管的屈曲失穩性能。Arjomandi等[4]通過計算得到外壓下屈曲壓力的解析解，推導出一個相對簡化的夾層管失穩壓力計算公式。Lopatin等[5]分析獲得了臨界載荷的近似解析公式，進行了驗證，同時考察了不同夾層材料對夾層管屈曲性能的影響。張磊[6]等在有初始缺陷的情況下對夾層管壓潰壓力與初始缺陷的關系進行研究，推導出初始缺陷與屈曲失穩壓力和屈曲傳播壓力之間的關系。黎之奇[7]等發現了夾層管在失穩過程中三層管發生屈曲現象的順序，并且找到了材料性能與夾層管失穩壓力的關系。龔順風[8]等對夾層管層間粘結性與屈曲傳播壓力的關系進行研究，分析得到層間粘結關系與屈曲傳播壓力之間的影響。陳牧原等[9]在研究中找到了提高夾層管失穩壓力的方法。

從以上文獻發現，前人對于夾層管特征值屈曲研究較多，特征值屈曲分析無法考慮真實結構存在的缺陷和非線性問題，但特征值屈曲分析可以為非線性屈曲分析提供參考，屈曲模態可以作為幾何缺陷的形狀，所以含缺陷的非線性屈曲分析更符合實際工程應用。本文針對以聚丙烯材料作為中間層的夾層管，利用非線性有限元分析方法，對夾層管進行建模計算，通過特征值屈曲分析產生的一階最大變形作為夾層管初始缺陷，對夾層管在外壓作用下的屈曲失穩壓力與壓潰壓力進行非線性分析，考察夾層管厚徑比等參數的影響，為夾層管的應用作出理論依據。

1 夾層管模型

1.1 夾層管的理論模型

夾層管屈曲失穩是指在深海下，夾層管受到的外壓超過一定界限時管道發生形變的現象。對夾層管失穩進行研究主要使用有限元軟件對管道的屈曲載荷進行計算，再與相關文獻進行對比驗證模型的可行性。在進行非線性屈曲分析之前進行線性屈曲分析，可以獲得理想平衡狀態附近的解，將線性屈曲分析獲得的一階解評估非線性屈曲分析失穩外壓，可以快速做出屈曲模型形狀，計算精確并有效節約計算時間。

特征值對應的臨界外壓pcr可通過式（1）和式（2）得出[10]。

Ke+λKσd=0（1）

pcr=λp（2）

式中：Ke為結構的彈性剛度矩陣;Kσ應力剛度矩陣;λ為特征值;d為特征值對應的特征向量;p為均布外壓，MPa。

1.2 夾層管有限元模型

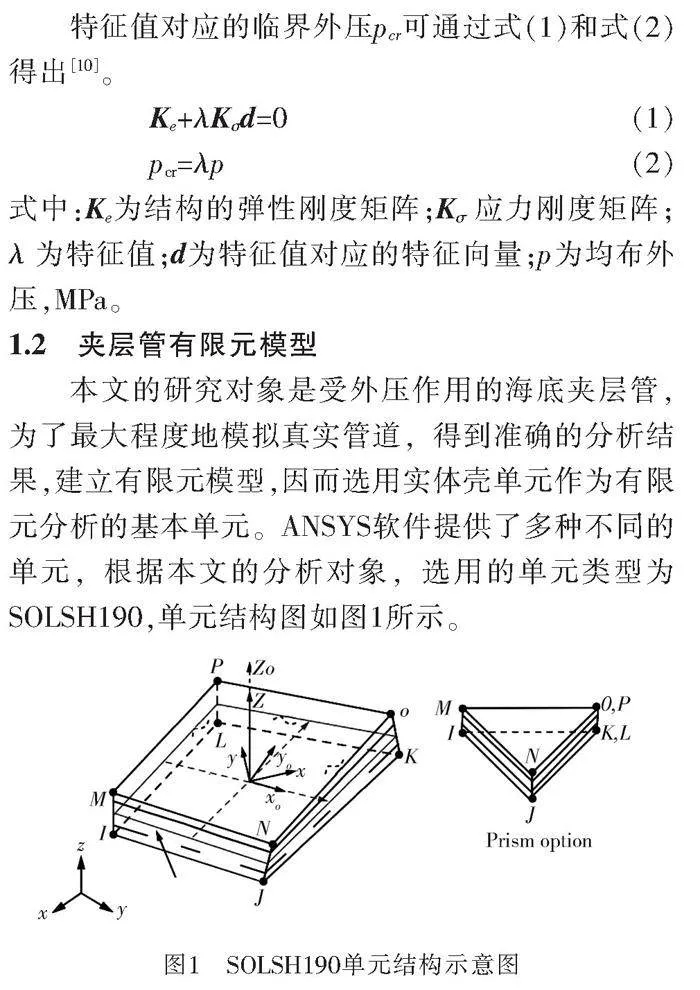
本文的研究對象是受外壓作用的海底夾層管，為了最大程度地模擬真實管道，得到準確的分析結果，建立有限元模型，因而選用實體殼單元作為有限元分析的基本單元。ANSYS軟件提供了多種不同的單元，根據本文的分析對象，選用的單元類型為SOLSH190，單元結構圖如圖1所示。

SOLSH190可以用于模擬薄壁和厚壁的殼結構，該單元具有八個節點，每個節點具有三個自由度：沿著節點x、y和z方向的平動[11]。因此，將SOLSH190與其他連續單元連接起來不需要額外的工作。SOLSH190具有塑性、超彈性、應力硬化、蠕變、大撓度和大應變能力[12]。它還具有混合U-P公式能力，用于模擬彈塑性材料和超彈性材料的變形。所以在對復合結構的模型建模時，如多層抗壓殼體或者三明治結構，適合使用SOLSH190單元進行建模。

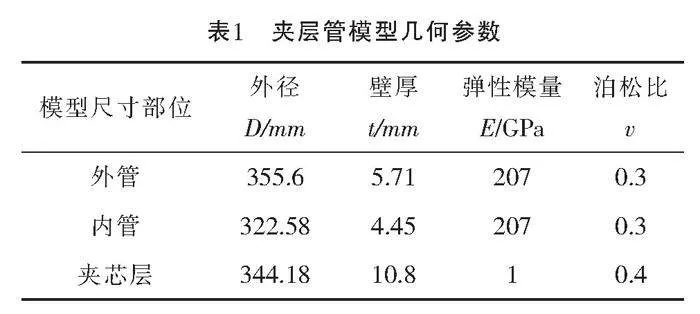
由于夾層管具有對稱性，為了節省計算資源，因此建立1/4管道模型，建模時認為在管道軸向上壁厚均勻分布。夾層管的內外管采用X65鋼管，夾芯層采用聚丙烯，夾層管模型幾何參數如表1所示。

在夾層管模型中，管道端部處的截面節點的位移自由度都被約束（x方向平動自由度、y方向平動自由度、z方向平動自由度），在管道外壁施加均布靜水壓力。夾層管截面模型如圖2所示。

2 夾層管受外壓失穩的特征值屈曲分析

2.1 無關性驗證

2.1.1 管道長度無關性驗證

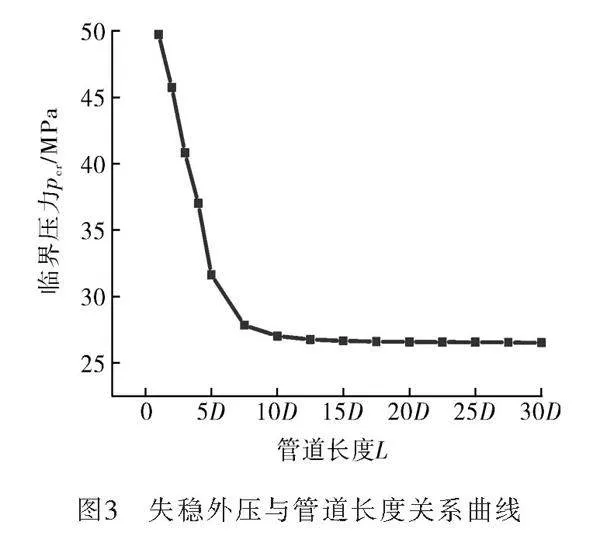
長度為幾百甚至上千公里的海底夾層管，在進行有限元分析時，受計算量的限制，很難對整條管道線路都進行分析。為了使計算結果不受長度的影響，對不同長度的夾層管進行失穩壓力分析并畫出曲線如圖3所示。隨著管長的增加，失穩壓力先降低，到達一定位置后趨于水平，即夾層管的失穩壓力不受管道長度影響，將曲線水平時的長度30D處的壓力作為夾層管的失穩壓力，使用此壓力進行后續分析。

2.1.2 管道網格無關性驗證

當網格數量大于一定值時，可以忽略網格數量對管道臨界外壓的影響，但是網格劃分的越精密，電腦的計算壓力就會越大，網格劃分的粗糙一些則會使結果計算不準確，所以，既要消除網格對計算的影響，又不影響結果的準確度，就需要選取合適的網格尺寸。

由圖4可知，當網格數量2 000～6 000時，誤差較大，網格數量引起的臨界壓力變化不能忽略;網格數量由6 000增加到12 000時，pcr逐漸減小;網格數量由12 000增加到15 000時，pcr基本不變。因此，確定劃分的網格數量為15 000。

2.2 屈曲模態

利用ANSYS進行屈曲分析，首先對管道進行特征值屈曲分析，此分析是在小變形情況進行的，即屈曲模態，目的是得出臨界荷載，一般取一階模態的，因為一階屈曲模態往往最容易發生，所以通常作為首選，夾層管一階線性屈曲模態如圖5所示[13]。管道長度為30倍外管直徑長度（30D），受均布外壓pcr=26.535 MPa作用。

2.3 模型驗證

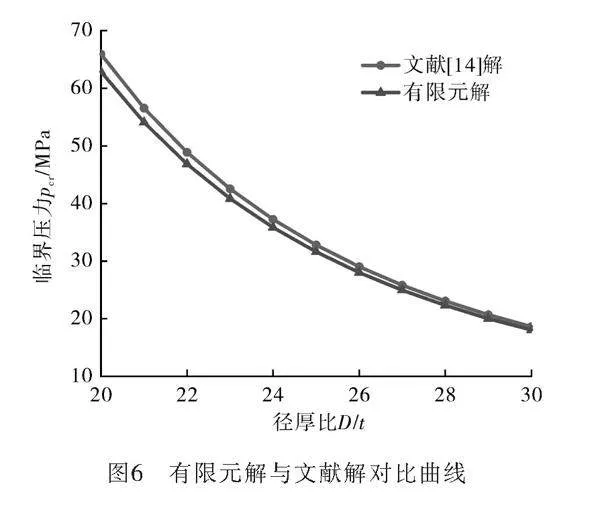
基于龔順風[14]的計算方法，對有限元計算模型進行驗證，計算結果曲線如圖6所示。可以看出，在管道直徑相同時，外壓隨著管道厚度的增大而減小，當徑厚比D/t為20時，有限元結果與文獻結果的誤差為4.6%，徑厚比為30時，誤差為3.0%。有限元計算得到壓力和文獻的計算結果最大誤差在5%以內，說明吻合度較好。故本文采用的模擬方法，可以作為判斷夾層管失穩壓力的評估依據。

3 夾層管受外壓失穩的非線性屈曲分析

研究夾層管受外壓失穩的屈曲解，一般有直接法和間接法兩種方法。直接法為增加一個擾動進而求出屈曲解，間接法以線性屈曲模態分析為基礎，加一個微小的初始變形，從而形成初始缺陷，再使用非線性屈曲分析方法研究屈曲解。

本文對夾層管非線性分析采用間接法，基于線性屈曲模態，對位移進行微小比例因子縮放，更新幾何模型達到施加缺陷的目的。使用線性屈曲獲得的屈曲解作為非線性屈曲的初始壓力，研究夾層受外壓管變形情況和在徑厚比不同時，失穩外壓的變化情況。在非線性計算過程中，外壓載荷隨載荷步數的逐漸增加而增大，迭代過程不收斂時停止，不收斂前的某一階載荷值即為非線性臨界失穩壓力[15]。

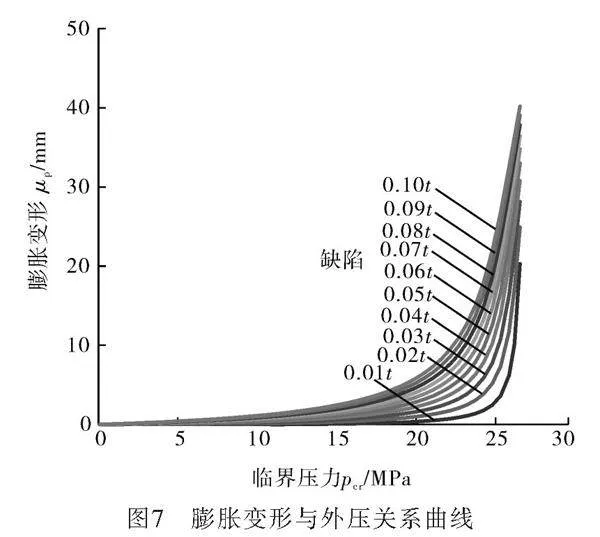
3.1 模態缺陷對夾層管最大變形量的影響

對夾層管進行非線性屈曲分析時，管道受到外壓后，在徑向會產生變形，包括壓縮變形us和膨脹變形up。使用有限元軟件計算在不同缺陷下的膨脹與壓縮變形量，并繪制曲線圖，如圖7～8所示。從圖中可以看出，二者具有相似的變化規律，當管道缺陷不變時，膨脹與壓縮變形量都隨著外壓的增大而增大，開始曲率低，變化速度慢，最后曲率高，變化速度快，管道壓縮變形量始終大于管道膨脹變形量，外壓為26.535 MPa，缺陷為0.1t時，壓縮變形量為50.74 mm，膨脹變形為40.197 mm，壓縮變形量比膨脹變形量大24.74%。在外壓相同時，壓縮變形量與膨脹變形量都隨著缺陷的增大而增大，外壓為26.535 MPa，缺陷在0.01t～0.10t范圍內時，壓縮量從23.017 mm增大到50.74 mm，增大120.45%，膨脹量從20.293" mm增加到40.197 50 mm，增大98.08%。

3.2 模態缺陷對夾層管沿軸向變形的影響

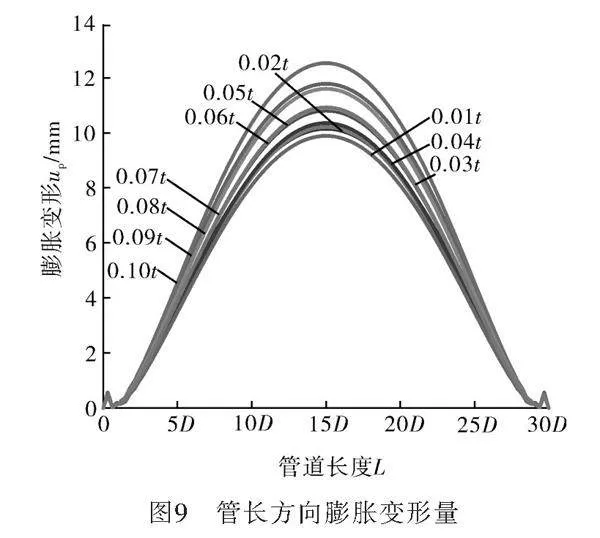
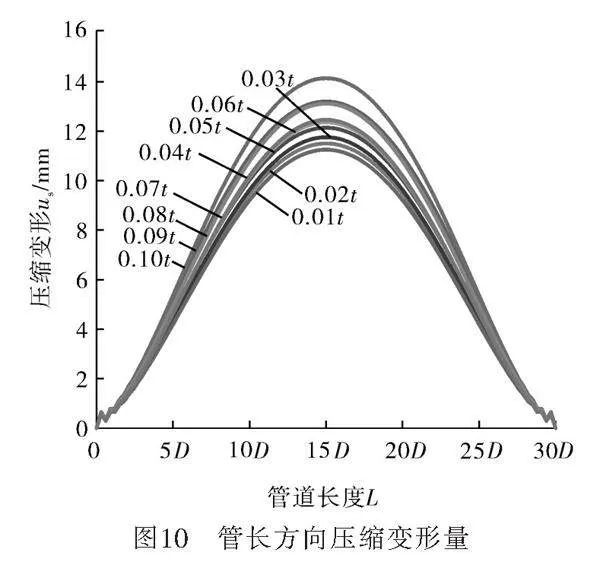
管道受到外壓作用以后，會使管道產生變形，隨著壓力增大，變形沿軸傳播。使用有限元軟件計算在不同缺陷下管長對應的的膨脹與壓縮變形量，通過計算結果繪制變化曲線，如圖9～10所示。

由圖9～10可以看出，兩張圖的規律相似，膨脹變形量與壓縮變形量都沿著管道長度先增加后減小，在管道正中間產生最大變形，由于管道兩端固定約束，變形為0。在缺陷相同的情況下，膨脹變形量大于壓縮變形量。隨著缺陷的增加，最大變形量也逐漸增大。

3.3 夾層管失穩壓力的判別方法研究

在以往研究中，是根據徑向位移隨外壓的變化情況來判斷管道達到臨界屈曲，當外壓達到一定值時，管道變形突然增大，在變形突然變化時所對應的壓力即為管道的失穩壓力，但這個失穩壓力只是一個大致范圍，不能準確判定管道的失穩壓力。

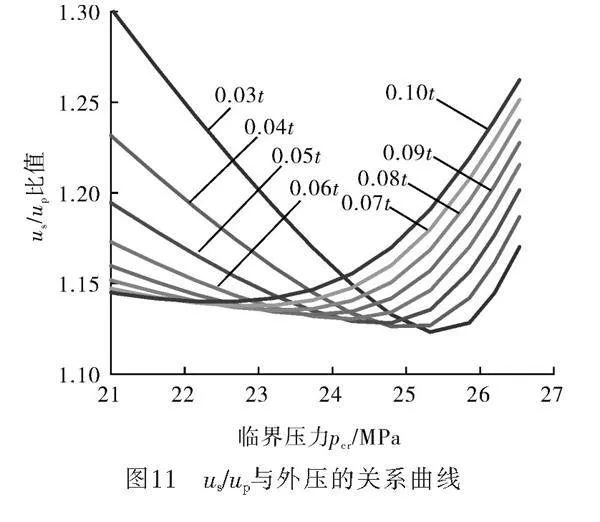
本文使用拐點法作為判定管道是否到達失穩壓力的方法，經過計算，管道受到外壓后，在徑向會產生壓縮變形us與up膨脹變形，并向著管軸方向傳播，壓縮變形量始終大于膨脹變形量，使用有限元軟件計算壓縮變形量與膨脹變形量并計算其比值us/up，繪制不同缺陷下us/up與外壓的曲線圖，如圖11。

由圖11可知， us/up先下降后上升，在某一時刻達到最低點，形成拐點。在拐點之前，up變化的速度大于us變化的速度，而在拐點之后，us變化的速度則大于up變化的速度，但兩者都一直在增大，即管道一直都在被壓縮，而且在拐點以后這種壓縮量突然變大，所以將此拐點所在的壓力值作為管道受壓的失穩壓力值。由圖11還可看出缺陷值越大，拐點出現的時間越早，即失穩壓力越小。

3.4 夾層管壁厚比對夾層管失穩壓力的影響

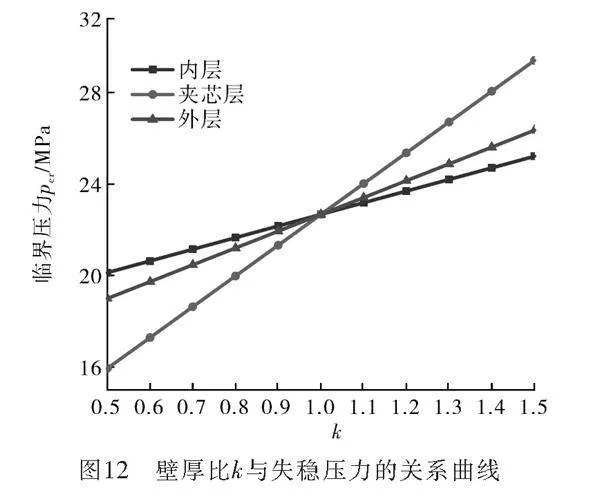
在夾層管應用過程中，內外管與夾芯層的壁厚比是一個非常重要的參數，對夾層管抗外壓能力、抗腐蝕能力和設計成本等方面都有著十分重要的影響。大多數研究者在分析失穩壓力與壁厚比時，都只研究外管與夾芯層，忽略了內管的作用。本文采用拐點法對夾層管進行分析，在0.1t的模態缺陷下，以表1中的尺寸為基準，分析各層壁厚比為0.5～1.5時的失穩壓力，如圖12。其中，k=t1/t，t1為設計壁厚，t為表1中的壁厚。

由圖12可知，對于增加內管、外管和夾芯層壁厚比的夾層管，它們的失穩壓力壓力都逐漸升高，其中斜率最大的是夾芯層，壁厚比從0.5～1.5，失穩壓力從15.94 MPa增大到29.41 MPa，增大84.5%，在相同條件下外管的失穩壓力增大38.75%，內管的失穩壓力增大25.29%。即夾芯層厚度變化對失穩壓力影響最大，可采取適當增加夾心層的厚度來提高夾層管抵抗外壓的能力。

4 結論

1） 含有模態缺陷的夾層管在受外壓屈曲過程中，會在管徑方向產生壓縮變形和膨脹變形，并沿軸向傳播，壓縮變形量始終大于膨脹變形量。變形沿管道中間截面軸對稱，變形量從夾層管的一端到管道中心逐漸增大，在管道正中間產生最大變形，變形量隨著缺陷的增大而增大，變形速度先慢后快。

2） 通過使用拐點法，即夾層管壓縮變形與膨脹變形的比值來判定夾層管是否達到失穩狀態，外壓增大時，比值先呈現降低趨勢，到達轉折點后快速增加，將曲線的轉折點所對應的壓力作為夾層管非線性屈曲的失穩壓力，失穩壓力隨著缺陷的增大而減小。

3） 使用上述判斷失穩壓力的方法，對壁厚比不同的內外管和夾芯層失穩外壓進行分析，在相同初始缺陷下，三者的失穩壓力都隨著壁厚比的增大而增大，改變夾芯層壁厚比的曲線斜率最大，即對夾芯層增加厚度可以有效增加夾層管抵抗外壓的能力。

參考文獻

[1] 管鋒，鄧一波，張良振，等.豎向外載作用下夾層海底管道凹陷行為研究[J].長江大學學報（自然科學版），2022，19（2）：63-71.

[2] 徐鶴，白宇晨，王哲，等.外壓作用下夾層管整體式止屈器止屈性能仿真研究[J].管道技術與設備，2021，（1）：42-47+51.

[3] Kardomateas G A， Simitses G J. Buckling of long sandwich cylindrical shells under external pressure[J]. Journal of applied mechanics， 2005， 72 （4）：493-499.

[4] Arjomandi K，Taheri F. Elastic buckling capacity of bonded and unbonded sandwich pipes under external hydrostatic pressure[J]. Journal of Mechanics of Materials and Structures，2010，（3）：391-408.

[5] Lopatin A V， Morozov E V. Buckling of the composite sandwich cylindrical shell with clamped ends under uniform external pressure[J]. Composite Structures， 2015， 122：209-216.

[6] 張磊，婁敏，季鵬，等.外壓作用下夾層管復合結構屈曲傳播分析[J].石油機械，2020，48（5）：114-120.

[7] 黎之奇，詹瑋.深水水下夾層管非線性屈曲特性[J].沈陽工業大學學報，2020，42（3）：330-336.

[8] 龔順風，王喜鵬，李根，等.層間黏結性能對夾層管屈曲傳播的影響機理[J].浙江大學學報（工學版），2018，52（5）：819-827+835.

[9] 陳牧原，張永茂，朱漢華.外壓作用下結構參數對夾層管屈曲性能的影響[J].科技通報，2016，32（4）：99-105+151.

[10] 雷明瑋，龔順風，胡勍.純彎作用下深海夾層管復合結構屈曲失穩分析[J].浙江大學學報（工學版），2015，49（12）：2376-2386.

[11] 劉秉奇，段夢蘭，付光明，等.夾層管屈曲傳播的數值模擬和夾芯層材料的選取[C]//第十七屆中國海洋（岸）工程學術討論會論文集（上）.2015.

[12] 付光明，彭玉丹，楊健坤，等.新型深水夾層管道靜水壓潰實驗設計[J].實驗室研究與探索，2019，38（12）：70-74.

[13] 田龍， 葉天源， 彭超，等.含初始缺陷海底管道外壓非線性屈曲研究[J].石油礦場機械， 2017， 46 （2）： 19-26.

[14] 龔順風，胡勍.外壓作用深海夾層管復合結構屈曲失穩分析[J].浙江大學學報（工學版），2014，48（9）：1624-1631.

[15] 王小龍，張強.含初始缺陷海底管道非線性屈曲失穩外壓判別方法研究[J]. 石油化工設備，2021，50（5）：32-37.

收稿日期： 2023-11-29

基金項目： 國家自然科學基金“高溫高壓多級壓裂管柱振動誘發封隔器蠕動失封機理研究”（52374034）。

作者簡介： 邊葉凱（1999-），男，黑龍江綏化人，碩士研究生，主要從事管道屈曲有限元分析研究，E-mail：2465036882

@qq.com。