準噶爾盆地東南緣頁巖油儲層脆性預測與評價

摘要：

準噶爾盆地東南緣二疊系中下部發育頁巖油致密儲層，脆性預測與評價對其勘探和開發有重要意義。本文利用巖石物理實驗、測井資料和疊前地震資料計算了準噶爾盆地東南緣二疊系頁巖油致密儲層脆性指數，對Rickman經典公式法、楊氏模量與泊松比比值法、拉梅系數法和剪切模量法進行了比較、分析與評價。研究認為：1）楊氏模量相對泊松比對巖性有更好的區分度，由拉梅系

數表征的泥巖分布率較高；2）根據文獻所得測井多參數計算脆性指數的方法應用效果不佳，在Castagna經驗公式換算橫波速度基礎上計算的脆性指數具有較好的應用效果；3）由YPD（Youngs modulusPoissons ratiodensity）式和LMR（拉梅系數密度）式反演的彈性參數變化率也能較好地指示有利儲層，尤以密度變化率為最佳，該屬性在扇三角洲前緣及分流河道特征上得到很好的展示；4）巖石物理實驗和實際資料應用均表明，ρE/σ為研究區脆性的最佳表征公式，效果好于Rickman經典公式與其他方法。

關鍵詞：

準噶爾盆地；致密儲層；頁巖油；巖石物理實驗；橫波速度；楊氏模量；泊松比；脆性指數

doi：10.13278/j.cnki.jjuese.20230140

中圖分類號：P631.4

文獻標志碼：A

于正軍，張軍華，周昊，等. 準噶爾盆地東南緣頁巖油儲層脆性預測與評價. 吉林大學學報（地球科學版），2024，54（5）：17111723. doi：10.13278/j.cnki.jjuese.20230140.

Yu Zhengjun， Zhang Junhua， Zhou Hao， et al.

Brittleness Prediction and Evaluation of Shale Oil Reservoir in Southeastern Margin of Junggar Basin. Journal of Jilin University （Earth Science Edition），2024，54 （5）：17111723.doi：10.13278/j.cnki.jjuese.20230140.

收稿日期：20230530

作者簡介：于正軍（1968-），男，教授級高級工程師，博士，主要從事油氣藏勘探綜合研究，E-mail：yuzj_789@163.com

通信作者：張軍華（1965-），男，教授，博士生導師，主要從事石油物探的教學與研究工作，E-mail：zjh@upc.edu.cn

基金項目：中石化先導項目（P21007）；國家自然科學基金項目（42072169）

Supported by the Sinopec Pilot Project （P21007） and the National Natural Science Foundation of China （42072169）

Brittleness Prediction and Evaluation of Shale Oil Reservoir in Southeastern Margin of Junggar Basin

Yu Zhengjun1， Zhang Junhua2， Zhou Hao2， Ren Ruijun1， Chen Yongrui2， Yang Yulong1

1. Geophysical" Research Institute of Shengli Oilfield Company， Sinopec， Dongying 257022， Shandong， China

2. School of Geosciences， China University of Petroleum， Qingdao 266580， Shandong， China

Abstract：

Shale oil tight reservoirs are developed in the middle and lower part of Permian in southeastern margin of Junggar basin. Brittleness prediction and evaluation are of great significance to its exploration and development. In this paper， the brittleness index of Permian tight reservoir in southeastern margin of Junggar basin is calculated by using petrophysical experiments， well logging data and prestack seismic data， and the Rickman classical formula method， the

method of ratio of

Youngs modulus and Poissons ratio， the Lamé coefficient method and the shear modulus method are compared， analyzed and evaluated. The results show that： 1） Compared with Poissons ratio， Youngs modulus has a better discrimination of lithology， and the mudstone distribution resolution represented by Lamé coefficient is higher; 2） The method of calculating brittleness index based on logging multi-parameters obtained in the literature has a poor application effect， but the brittleness index calculated on the basis of converting shear wave velocity by Castagnas formula has a good application effect; 3） The change rates of elastic parameters inverted by YPD （Youngs modulusPoissons ratiodensity） formula and LMR （Lamé coefficientdensity） formula can also indicate favorable reservoir， especially the density change rate is the best， and the characteristics of upper fan delta front and distributary channel can be well demonstrated by this attribute; 4） Petrophysical experiments and actual data applications show that ρE/σ is the best characterization formula of brittleness in the study area， and the effect is better than Rickmans classic formula and other methods.

Key words：

Junggar basin;" tight reservoir; shale oil; petrophysical experiment;" shear wave velocity; Youngs modulus; Poissons ratio; brittleness index

0" 引言

脆性是非常規油氣藏勘探開發的重要參數，反映物體受力變形時發生破裂的性質，與延性、彈性、塑性等都屬于巖石的力學特性。脆性大小一般通過脆性指數來衡量，其計算方法主要包括礦物含量占比法、巖石物理實驗測量法、測井資料換算法和地震疊前反演法等。Rickman等［1］對楊氏模量和泊松比進行歸一化并取二者的平均值作為脆性指數。Goodway等［2］用拉梅常數進行組合來表示脆性指數。Guo等［3］利用楊氏模量和泊松比的比值描述脆性。張豐麒等［4］將Zoeppritz方程推廣為BI-Zoeppritz方程，直接反演脆性指數。Zhang等［5］基于AVO（amplitude variation with offset）理論和多孔介質理論推導出脆性反演方程。張瑞等［6］使用冪指數經驗公式代替Aki近似方程中的密度項，建立了一套直接反演巖石脆性參數的方法。劉慶等［7］將灰色關聯方法與層次分析相結合，為脆性指數的預測提供了新思路。

在前人研究的基礎上，本文從準噶爾盆地（簡稱準）東南緣取心井的巖石物理實驗出發，分別用Rickman經典公式法、楊氏模量與泊松比比值法、拉梅系數法等方法計算脆性指數，分析脆性指數的分布特點；采用測井多參數法，以聲波時差轉換得到的縱波速度和多種方法獲得的橫波信息計算井的脆性指數，并與錄井進行對比驗證；優選角度域的疊前數據體，利用小、中、大三個角度的疊前資料直接反演彈性參數變化率數據體，并由此估算脆性，開展測井約束彈性參數疊前反演；最后對變化率（反射系數）預測的脆性指數和彈性參數反演的脆性指數進行分辨率與信噪比評價，為研究區二疊系致密油的勘探開發以及類似勘探新區開展脆性預測提供參考。

1" 研究區概況

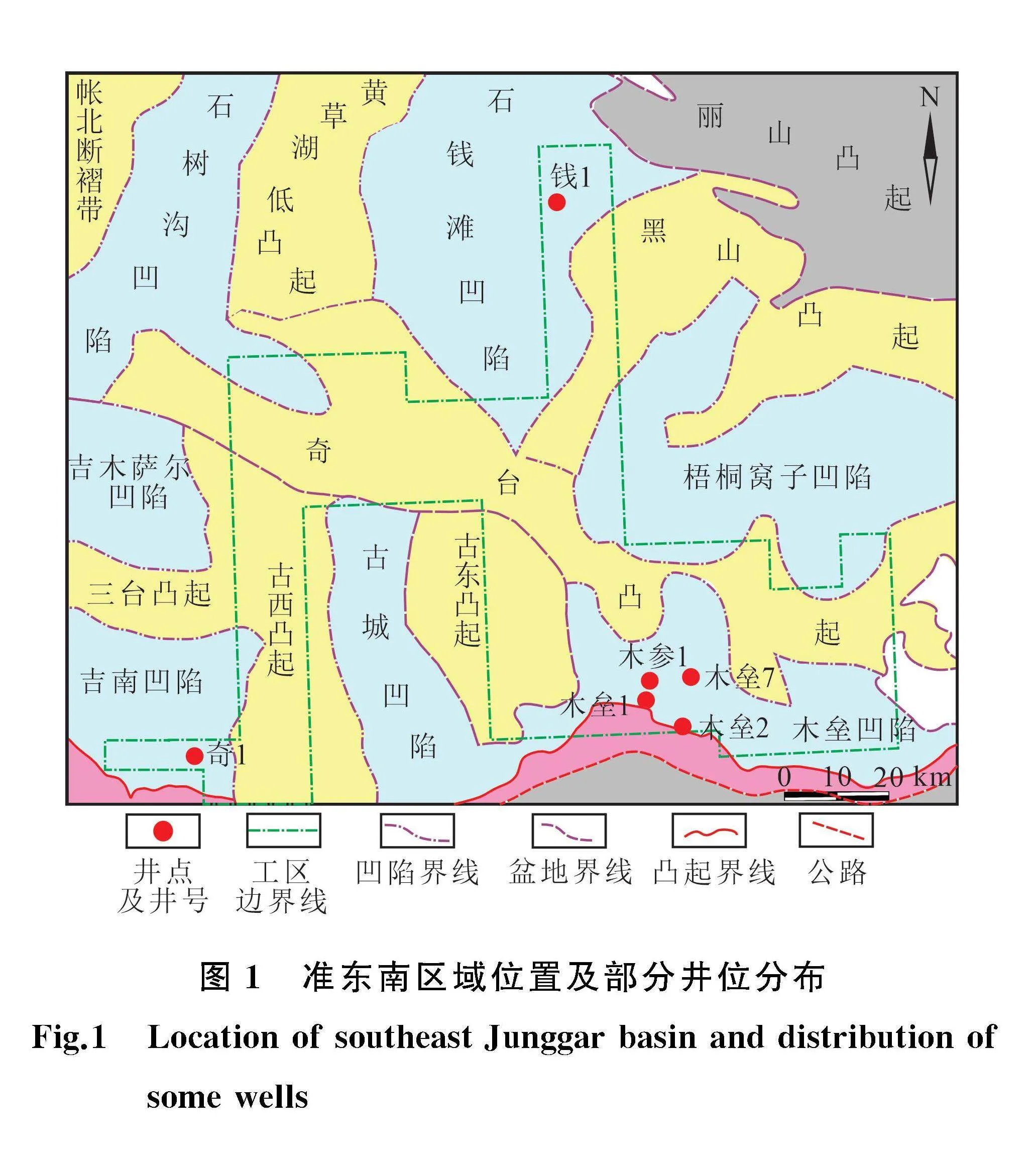
準噶爾盆地東南緣發育多個殘留凹陷，包括石錢灘凹陷、梧桐窩子凹陷、木壘凹陷、古城凹陷、吉南凹陷、吉木薩爾凹陷、石樹溝凹陷等（圖1）。其中：吉木薩爾凹陷已探明豐富的二疊系頁巖油地質儲量，實現了規模化勘探開發［8］；石錢灘凹陷石錢1井發現了自生自儲的石炭系碎屑巖構造巖性油氣藏；

吉南凹陷薩探1井在二疊系鉆遇了371 m厚的烴源巖［9］。石錢灘凹陷錢1井，木壘凹陷木參1井、木壘1井和木壘2井近來又有了新的油氣發現，這也展示了準東南緣良好的油氣勘探前景。

準東南二疊系以沙奇凸起為界，北部一般以平地泉組（P2p）命名，南部以蘆草溝組（P2l）命名［10］。不同區塊巖性有所不同，吉木薩爾凹陷二疊系蘆草溝組主要發育湖相云質混積巖，石樹溝凹陷平地泉

組白云石、方沸石體積分數較高，發育灰巖、砂巖及砂礫巖［813］。準東南二疊系儲層具有鄰源供烴、自生為主、原位聚集的典型陸相頁巖油特點［14］。

對于致密油勘探開發來說，儲層描述除了物性、含油性以外，脆性也是重要的衡量指標。準東南區塊地域遼闊，勘探面積達8 674 km2，但已鉆探井較少。充分利用有限的取心、錄井、測井與地震資料開展脆性指數計算與評價，具有客觀必要性。

2" 基于巖石物理實驗的脆性計算與評價

利用巖石物理實驗測試巖石樣品的楊氏模量、泊松比，再根據Rickman經典公式（表1）即可計算巖石的脆性指數［1］。還可以根據彈性參數的物理含義，計算表征脆性特性的屬性（它們的量值不在［0， 1］之間，本文稱之為類脆性指數），如表1中的楊氏模量與泊松比比值法［3］、拉梅系數法［2］與剪切模量法［2］。

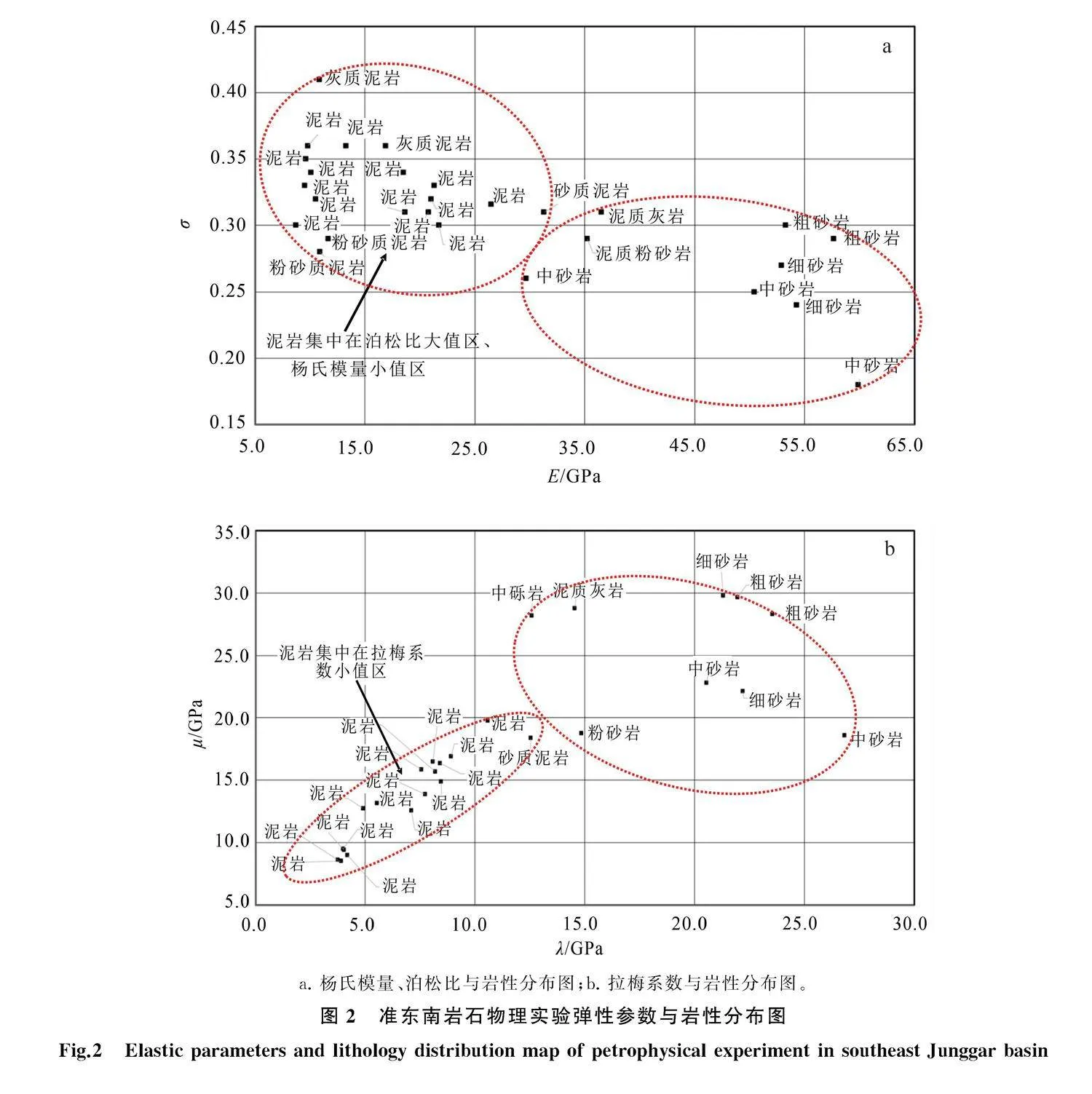
對研究區29塊巖樣進行巖石物理實驗，測得彈性參數與巖樣的巖性分布如圖2所示。從圖2可以看出，泥巖楊氏模量小、泊松比大、拉梅系數小，根據表1公式分析可知，脆性指數小；反之，砂巖、灰巖等，楊氏模量大、泊松比小、拉梅系數大，脆性強。對圖2a進一步觀察還能發現，楊氏模量相對泊松比對巖性有更好的區分度；從圖2b可以看出，由拉梅系數表征的泥巖分布更集中，分辨率高于楊氏模量泊松比分布。

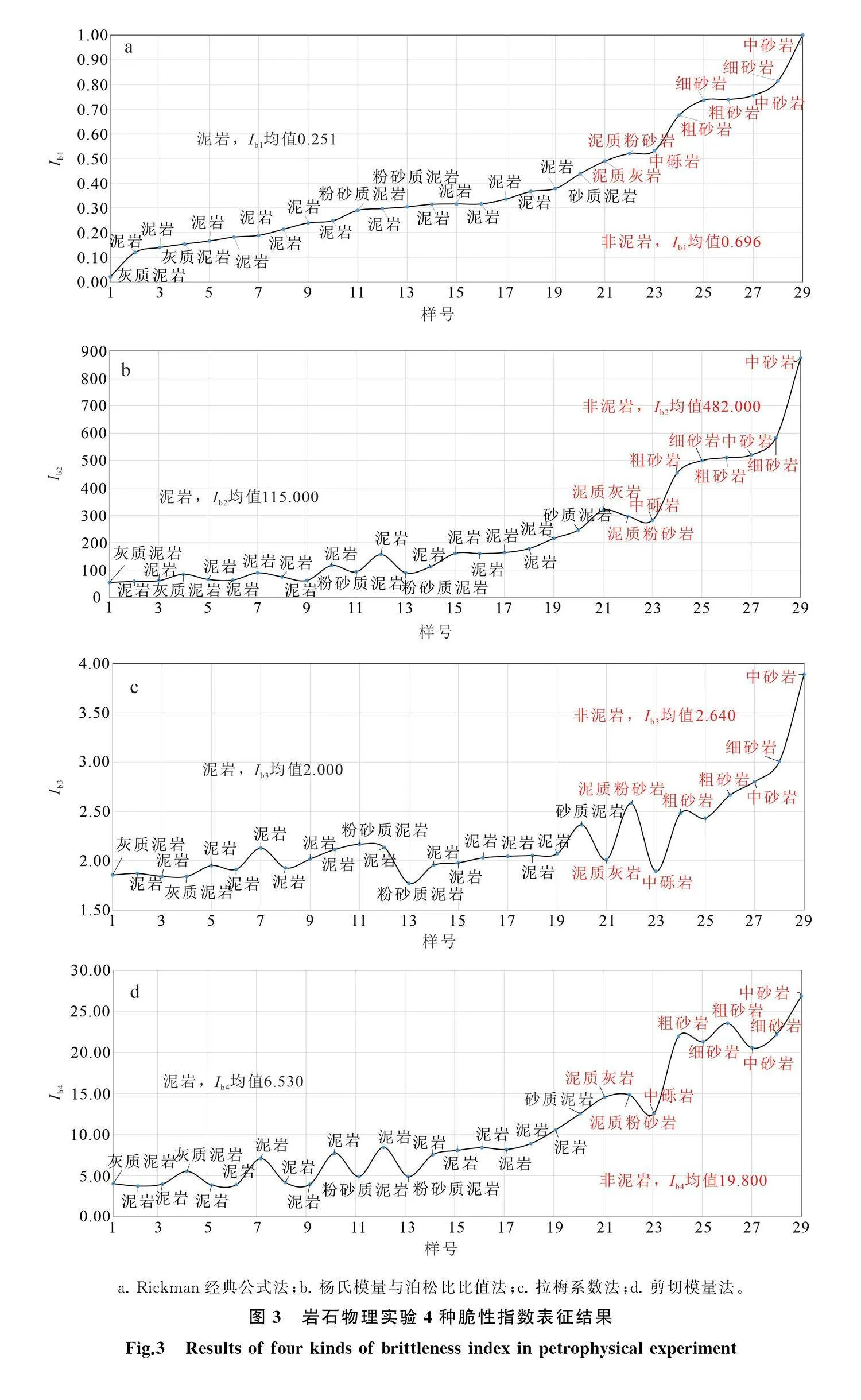
用表1所示公式計算每塊樣品的脆性或類脆性指數，按同一順序排列，結果如圖3所示。由圖3a可以看到：1）泥巖與非泥巖（灰巖、砂巖等）的脆性指數有較好的區分度；2）泥巖的平均脆性指數為0.251，非泥巖的平均脆性指數為0.696，二者比值為2.77，一定程度上可反映區分巖性的能力。圖3b基本結論同圖3a，非泥巖與泥巖的類脆性指數均值比

為4.19，高于第一種方法。由圖3c可以看到，21號灰巖、23號礫巖的類脆性指數低于泥巖，這是反常規的錯誤結果，而且非泥巖與泥巖的類脆性指數均值比為1.32，是4種方法中最低的。圖3d中20號泥巖樣本與后續礫巖樣本也很難區分，不過非泥巖與泥巖的類脆性指數均值比為3.03，處于4種方法的第2位。綜合以上認識，4種脆性指數評價方法中，楊氏模量與泊松比比值法云質巖、灰巖、砂巖等巖性的楊氏模量大、泊松比小，具有放大甜點的效應，區分泥巖與非泥巖的能量最強，為最佳表征方法，其次為剪切模量法，再次為Rickman經典公式法，拉梅系數法最差。

3" 測井多參數脆性計算與比較

3.1" 測井多參數經驗公式直接計算脆性指數

一口井的取心段有限，而且也不是每口井都取

心，因此，用巖石物理實驗計算脆性是很有限的。測井是評價儲層的很好手段，井的脆性指數可通過測井參數計算得到。

袁思喬等［15］在研究松遼盆地大情字井油田白堊系青山口組一段致密砂巖儲層時，得出了聲波時差AC（AC）、密度DEN（ρ）、電阻率（Rt）、自然伽馬GR（GR）、補償中子GNL（Cnl）等5種測井參數與脆性指數的關系，其中ρ、Rt與脆性正相關，其他三種測井曲線與脆性負相關，測井曲線計算前都做歸一化處理，計算公式為

Ibw1=

15（

0.32ρ+0.13Rt+0.41AC+0.08Cnl+0.06GR）×100%。（1）

付娟娟等［16］研究了山西沁水盆地石炭系—二疊系頁巖儲層脆性指數與測井響應間的關系，得出以下關系式：

Ibw2=33.6ρ-0.05Rt-8.6GR-0.01AC。 （2）

3.2" 利用橫波速度換算脆性指數

利用聲波時差可以換算縱波速度，如果有橫波時差，可用彈性參數之間的關系獲取楊氏模量與泊松比，進而計算井段的脆性指數。

a. Rickman經典公式法；b. 楊氏模量與泊松比比值法；c. 拉梅系數法；d. 剪切模量法。

E=ρ3v2P-4v2S（vP/vS）2-1； （3）

σ=0.5（vP/vS）2-1（vP/vS）2-1。 （4）

式中：vS為橫波速度；vP為縱波速度。

3.2.1" 利用橫波速度與其他測井曲線的統計關系獲取

楊秀春等［17］在研究鄂東氣田韓城礦區煤巖地層時，得出了橫波時差與縱波時差、密度的如下關系：

ΔtS=ρΔt2P0.4105ΔtP+322.36ρ-478.41。" （5）

式中：ΔtS為橫波時差；ΔtP為縱波時差。

孫玉凱等［18］在研究吐哈油田勝北地區的巖性油

氣藏時，得到了橫波時差與補償中子、電阻率、密度之間的關系：

ΔtS=215.69CnlρRt+111.34。（6）

趙炎［19］給出了橫波時差的以下計算公式：

ΔtS=ΔtP{1-1.15［（1/ρ+1/ρ3）/（e1ρ）］}1.5。 （7）

3.2.2" 利用巖石物理實驗橫波與縱波速度關系獲取

Castagna等根據不同巖性，給出了不同換算公式［20］：

1）白云巖地層：

vS=0.583vP-0.078。（8）

2）飽含水凈砂巖：

vS=0.804vP-0.856。（9）

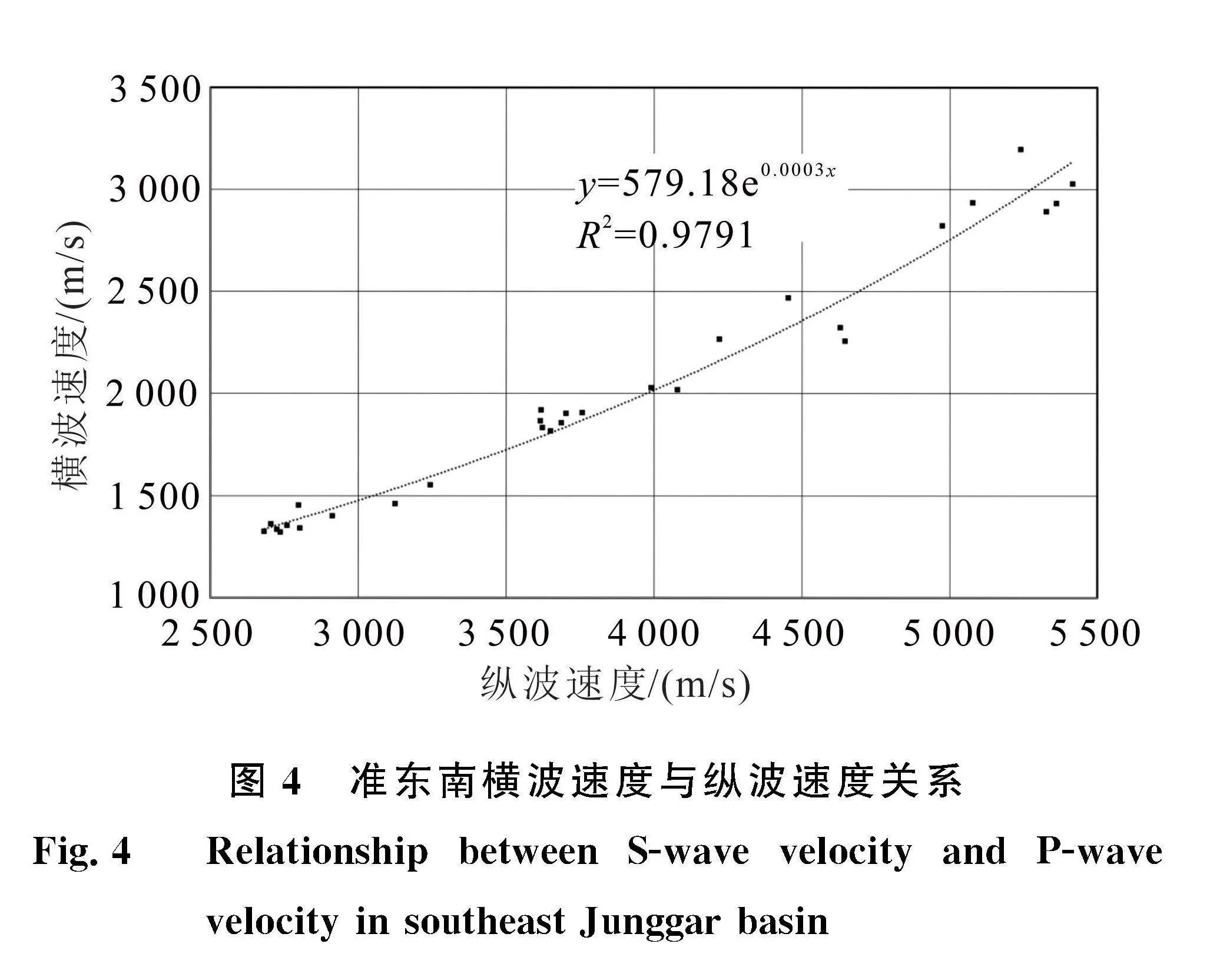
本文通過準東南4口井29塊巖樣的巖石物理實驗，統計出了橫波速度與縱波速度的關系（圖4）：

vS=579.18e0.0003vP。（10）

從圖4可以看出，橫波速度與文獻［1720］給出的規律類似，基本呈線性關系，擬合度較高。

3.3" 研究區井脆性指數計算與比較

以錢1井二疊系平地泉組云質巖甜點段和木壘1井蘆草溝組二段2砂組灘壩砂儲層、一段2砂組扇三角洲砂體為研究對象，用多種方法計算脆性指數，并進行比較和評價。

3.3.1" 錢1井

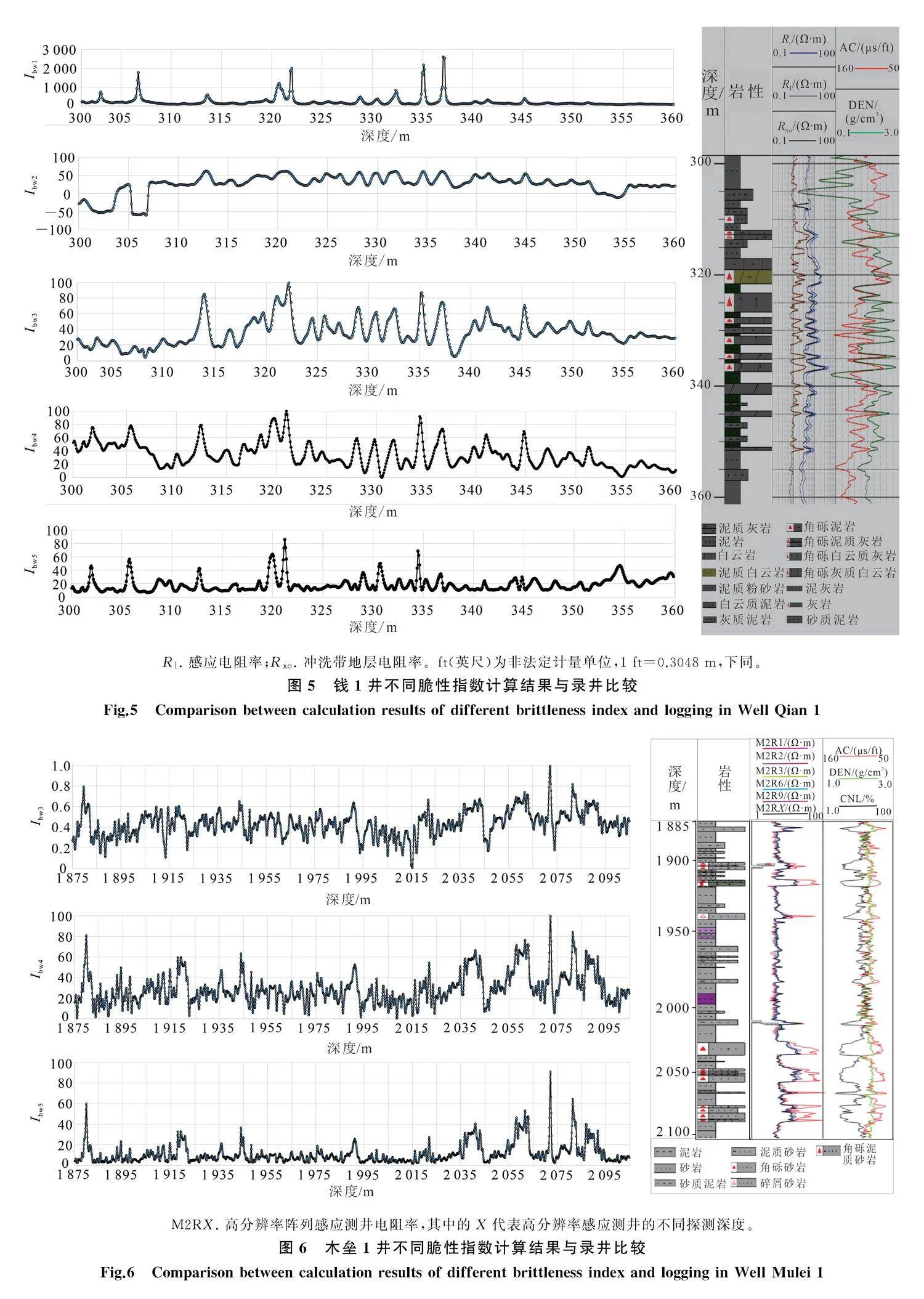
對于錢1井，首先直接由測井多參數計算脆性指數Ibw1（式（1））、Ibw2（式（2））（圖5）。分析可知：1）Ibw1集中在幾個峰值，DEN與Rt曲線的貢獻率很高，部分異常漏檢（如DEN曲線所在325 m處的白云質灰巖）；2）Ibw2存在負值，甜點段曲線缺乏差異性，不適合錢1井區，原因是計算公式的系數對研究工區不合適。

然后分別利用趙炎經驗公式、Castagna經驗公式和巖石物理實驗方法計算脆性指數，即Ibw3由式（7）換算，Ibw4由式（8）換算，Ibw5由式（10）換算（圖5）。縱波速度從測井數據中獲取，根據式（3）（4）分別計算楊氏模量和泊松比，再利用Rickman經典公式計算脆性（為了便于數值比較，不采用表1中其他方法）。可以看出：1）Ibw3、Ibw4曲線特征基本類似，Ibw4在306 m Rxo曲線處的泥質粉砂巖得到有效識別，效果好于Ibw3；2）巖石物理實驗得到的Ibw5總體與錄井吻合較好，但355 m處Rt曲線處的泥巖脆性偏高。概括來說，對于錢1井區，因為目的層段云質巖發育，取心又少，由Castagna經驗公式統計分析白云巖縱橫波速度關系為佳。

3.3.2" 木壘1井

對于木壘1井，分別利用趙炎經驗公式、Castagna經驗公式和巖石物理實驗方法計算脆性指數，即Ibw3由式（7）換算，Ibw4由式（9）換算，Ibw5由式 （10）換算。縱波速度從測井數據中獲取，根據式（3）（4）計算楊氏模量和泊松比，再利用Rickman經典公式計算脆性。將計算結果與錄井進行比較，如圖6所示。可以看到，木壘1井的砂巖脆性強，3種方法大部分砂巖儲層都能得到較好的指示。但Rxo曲線的幾處薄砂巖，巖石物理實驗指示的脆性

Rl. 感應電阻率；Rxo. 沖洗帶地層電阻率。ft（英尺）為非法定計量單位，1 ft=0.3048 m，下同。

calculation results of different brittleness index and logging in"" Well Qian 1

M2RX. 高分辨率陣列感應測井電阻率，其中的X代表高分辨率感應測井的不同探測深度。

（Ibw5）不大，效果不如其他方法；而在Rt曲線表示的含油儲層段內，巖石物理實驗（Ibw5）的區分度好于其他2種方法。相對而言，巖石物理實驗計算的脆性是3種方法中最好的。

總的來說，對于本文這樣少井的新區，如果沒有橫波測井，用趙炎經驗公式（式（7））、Castagna經驗公式（式（8）、式（9））或巖石物理實驗結果換算的橫波也基本上可以得到與錄井比較一致的脆性指數，并以巖石物理實驗相對為好。

4" 基于疊前反演的脆性表征方法

用礦物組分、巖石物理實驗和測井資料換算只能得到目標點或目標層段的脆性，要得到脆性的區域分布，須用疊前資料反演彈性參數，再用一定的表征公式計算脆性指數。

疊前反演經典公式是Aki amp; Richards近似式［21］，它是關于縱橫波速度、密度與反射系數的關系式：

R（θ）=

sec2θ2ΔvPvP-4v2Sv2PΔvSvS+（12-2v2Sv2Psin2θ）Δρρ。（11）

式中：R（θ）為反射系數；θ為入射角和透射角的均值；ΔvP、ΔvS、Δρ分別為反射界面上下的縱波速度差、橫波速度差和密度差。

由于式（11）表示的速度變化率與脆性的關聯度還不是很強，為此利用彈性參數之間的關系，得到其他多種反演公式，如楊氏模量泊松比密度（Youngs modulusPoissons ratiodensity， YPD）反演式［22］：

R（θ）=（14sec2θ-2ksin2θ）ΔEE+14sec2θ（2k-3）（2k-1）2k（4k-3）+2ksin2θ1-2k3-4kΔσσ+（12-14sec2θ）Δρρ。（12）

式中：k為橫波速度與縱波速度的比值；ΔE、Δσ分別為反射界面上下的楊氏模量差、泊松比差。式（12）要求解楊氏模量、泊松比、密度的變化率（或稱反射系數）三個變量，給定與θ有關的3個角度域道集，近似為R（θ），即可聯立求解方程。

還有拉梅系數密度（LMR）反演式［2］：

R（θ）=（14-12k2）Δλλsec2θ+（12sec2θ-2sin2θ）k2Δμμ-14（1-tan2θ）Δρρ。 （13）

式中，Δλ、Δμ為反射界面上下的拉梅系數差。

除了以上方法外，還有學者直接反演流體體積模量、孔隙度［5］，以及用4個角度數據反演出4個彈性參數：流體項、楊氏模量、泊松比、密度［23］。

上述方法和計算公式反演的是彈性參數變化率或反射系數，在井和地層結構約束下可以得到真實的彈性阻抗和各種彈性參數，再進一步換算、表征脆性指數。

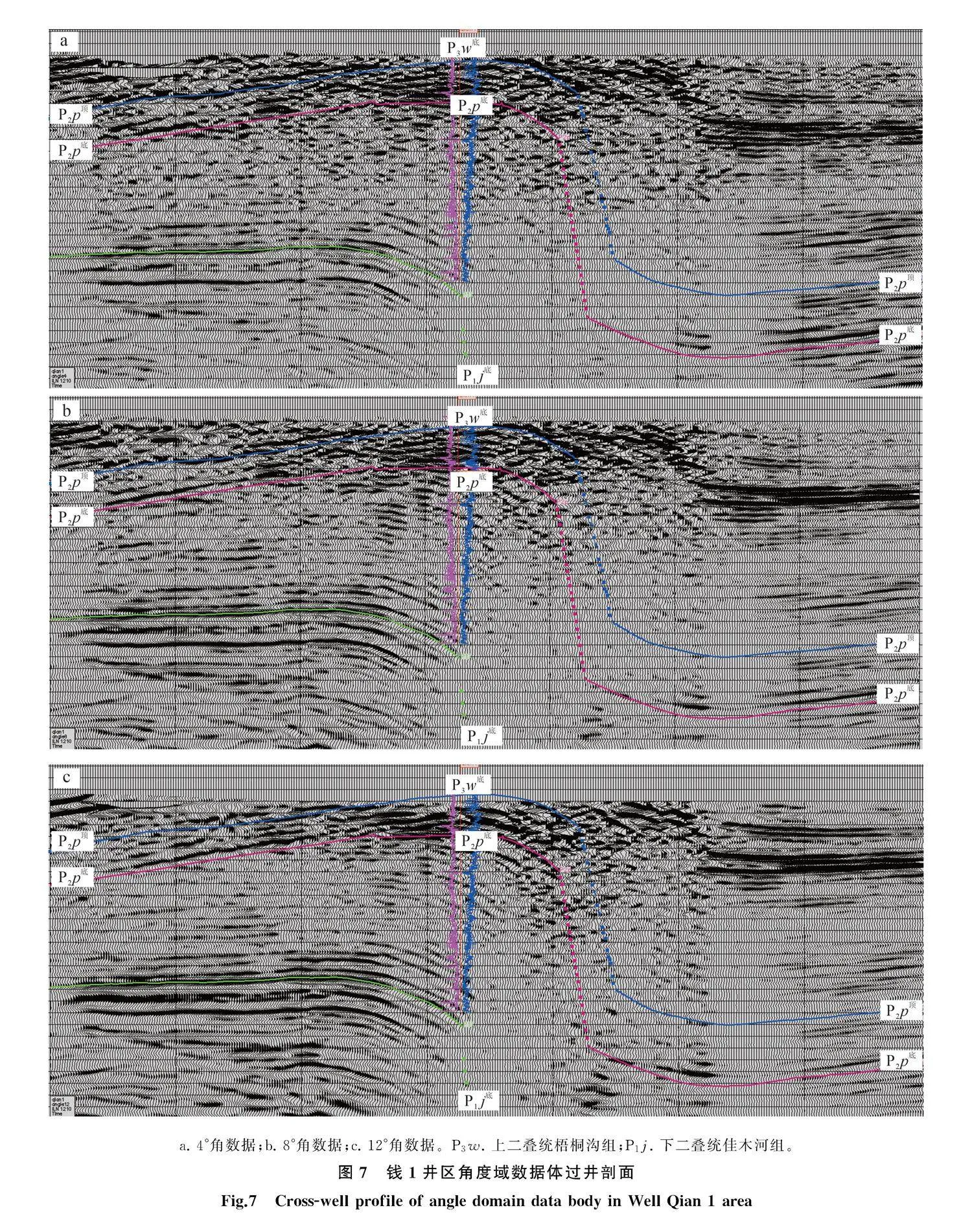
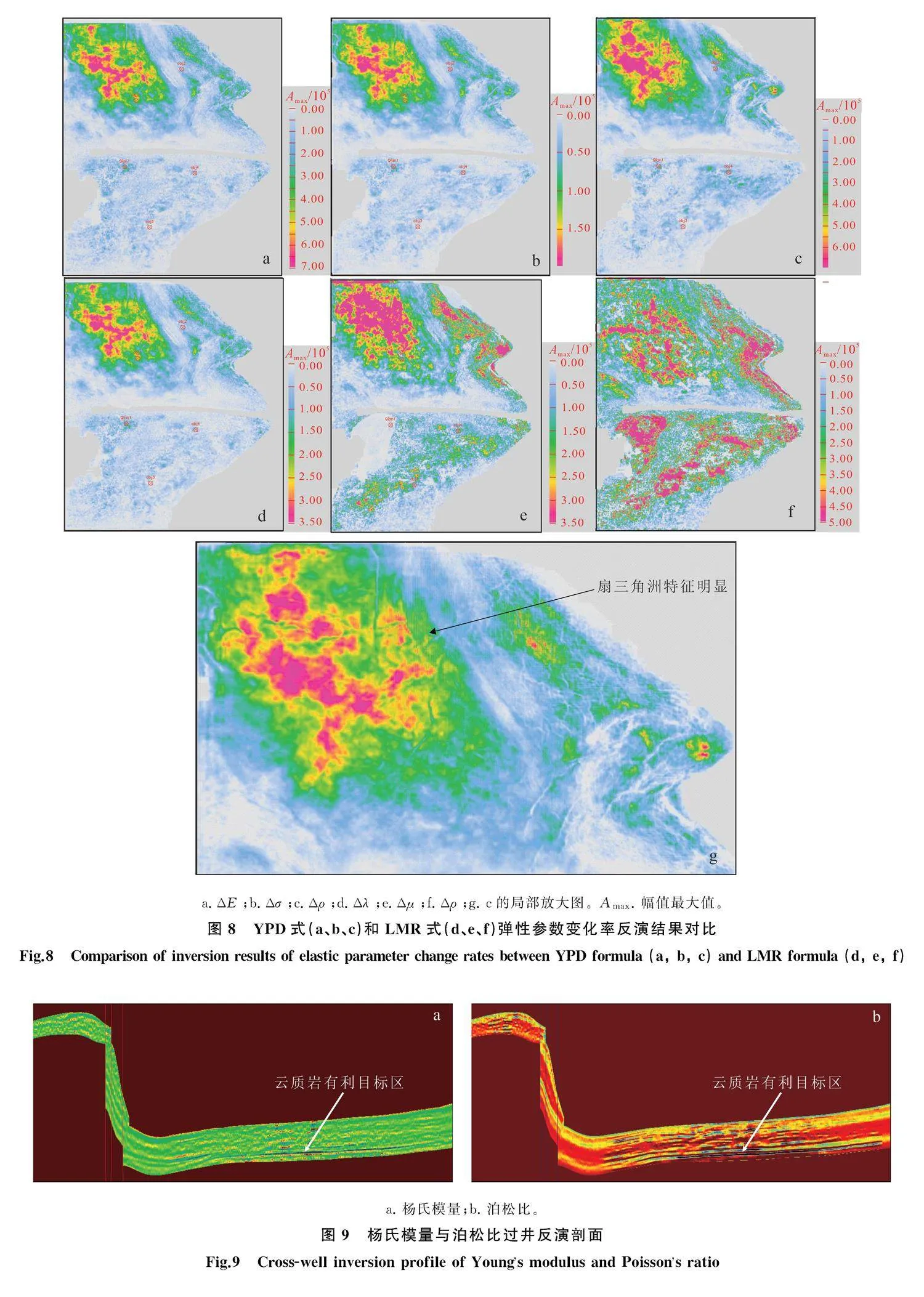
將以上方法應用到準東南錢1井工區，利用如圖7所示小、中、大3個角度的數據體進行彈性參數變化率反演。圖8展示了平地泉組下部甜點的沿層反演切片。我們驚喜地發現，YPD式反演的密度變化率有很好的反演效果。如圖8g，研究區西北部扇三角洲前緣及分流河道特征得到很好體現，與地質認識相符，指示了本區云質巖有利發育區。

通過巖石物理實驗計算橫波時差曲線，在井和地層結構的約束下，筆者反演了彈性阻抗和多種彈性參數，圖9展示了楊氏模量和泊松比過井反演剖面。從圖9可以發現，楊氏模量相對泊松比剖面信噪比更高，對云質巖有更好的識別度，反演結果與圖2a巖石物理實驗結果一致。

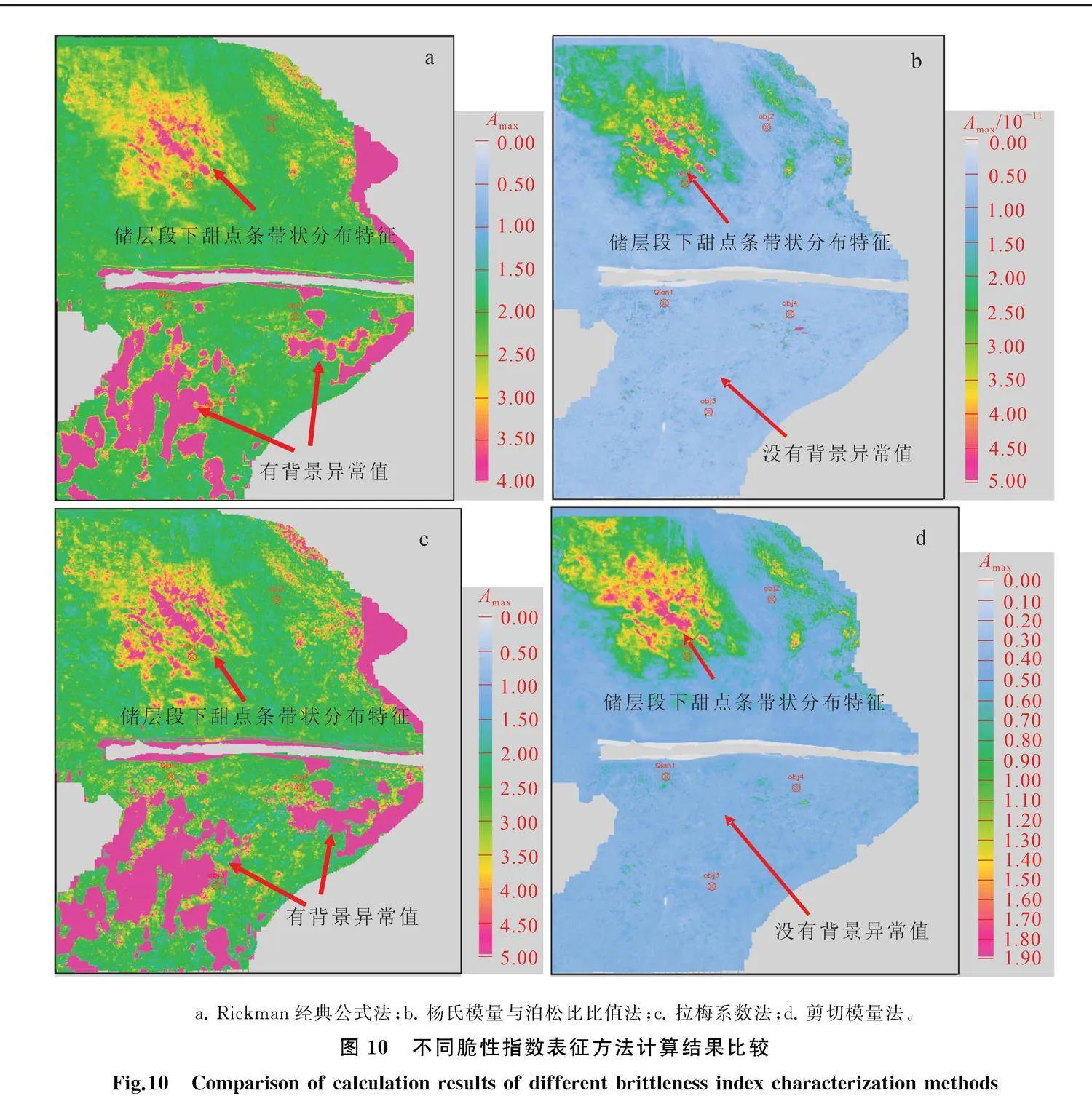
根據多種彈性參數反演結果，用表1所示的脆性指數表征公式計算了錢1井區的云質巖發育段沿層脆性指數，結果如圖10所示。與密度變化率等彈性參數進行比較，井約束反演指示的脆性有利帶也在研究區的西北部，預測部位大體一致；但脆性指數有條帶狀甜點特征。其中：Rickman經典公式法（圖10a）和拉梅系數法（圖10c）兩種方法目標區信噪比較高，但它們在研究區的南部存在野值；而楊氏模量與泊松比比值法（圖10b）和剪切模量法（圖10d）兩種方法沒有野值。總體來看，反演所得脆性指數認識與圖3所示巖石物理實驗表征結果完全一致，楊氏模量與泊松比比值法用到了彈性參數楊氏模量與泊松比的比值，大的楊氏模量除以小的泊松比具有更明顯的脆性特征，具有類似甜點屬性的優勢，值得推廣使用。

5" 結論

準東南二疊系蘆草溝組/平地泉組發育頁巖油致密層，脆性是儲層評價的重要指標。利用獲取的29塊取心樣品、多口井的測井資料以及疊前三維地震數據體，用多種方法對脆性指數進行了計算、比較與評價。

1）巖石物理實驗結果表明，楊氏模量是比泊松比更好的彈性參數。

2）井脆性指數分析表明，Castagna經驗公式具有很好的適用性。

3）密度變化率直接反演具有分辨率高的特點，可以較好地表征儲層的沉積特征。

4）相較于Rickman經典公式，用楊氏模量與泊松比的比值來表征脆性物理意義明確，應用效果更好，值得進一步推廣使用。

參考文獻（References）：

［1］" Rickman R， Mullen M， Petre E， et al. A Practical Use of Shale Petrophysics for Stimulation Design Optimization： All Shale Plays Are not Clones of the Barnett Shale［C/OL］//SPE Annual Technical Conference and Exhibition［20240301］. doi： 10.2118/SPE115258MS.

［2］" Goodway B， Perez M， Varsek J， et al. Seismic Petrophysics and Isotropic-Anisotropic AVO Methods for Unconventional Gas Exploration［J］. The Leading Edge， 2010， 29（12）： 15001508.

［3］" Guo Z Q， Chapman M， Li X Y. A Shale Rock Physics Model and Its Application in the Prediction of Brittleness Index， Mineralogy， and Porosity of the Barnett Shale［C］//SEG Technical Program Expanded Abstracts. Houston： Society of Exploration Geophysicists， 2012： 15.

［4］" 張豐麒， 魏福吉， 王彥春， 等. 基于精確Zoeppritz方程三變量柯西分布先驗約束的廣義線性AVO反演［J］. 地球物理學報，2013，56（6）： 20982115.

Zhang Fengqi， Wei Fuji， Wang Yanchun， et al. Generalized Linear AVO Inversion with the Priori Constraint of Trivariate Cauchy Distribution Based on Zoeppritz Equation［J］. Chinese Journal of Geophysics， 2013， 56（6）： 20982115.

［5］" Zhang S， Huang H D， Dong Y P， et al. Direct Estimation of the Fluid Properties and Brittleness via Elastic Impedance Inversion for Predicting Sweet Spots and the Fracturing Area in the Unconventional Reservoir［J］. Journal of Natural Gas Science and Engineering， 2017， 45： 415427.

［6］" 張瑞， 文曉濤， 楊吉鑫， 等. 楊氏模量和泊松比反射系 數近似方程及地震疊前反演［J］. 石油地球物理勘探， 2019，54（1）： 145153.

Zhang Rui， Wen Xiaotao， Yang Jixin， et al. Two-Term Reflection Coefficient Equation with Young’s Modulus and Poisson Ratio and Its Prestack Seismic Inversion［J］. Oil Geophysical Prospecting， 2019， 54（1）： 145153.

［7］" 劉慶，張鎮，楊帥，等．基于灰色關聯與層次分析的脆性指數預測方法：以準噶爾盆地吉木薩爾凹陷蘆草溝組致密儲層為例［J］．物探與化探，2023，47（4）：944953.

Liu Qing， Zhang Zhen， Yang Shuai， et al. Method for Brittleness Index Prediction Based on Grey Correlation and Analytic Hierarchy Process： A Case Study of the Tight Reservoirs in the Lucaogou Formation of the Jimusaer Sag， Junggar Basin［J］. Geophysical and Geochemical Exploration， 2023， 47（4）： 944953.

［8］" 宋永，周路，郭旭光，等． 準噶爾盆地吉木薩爾凹陷蘆草溝組湖相云質致密油儲層特征與分布規律［J］． 巖石學報，2017，33（4）：11591170．

Song Yong， Zhou Lu， Guo Xuguang， et al. Characteristics and Occurrence of Lacustrine Dolomitic Tight-Oil Reservoir in the Middle Permian Lucaogou Formation， Jimusaer Sag， Southeastern Junggar Basin［J］. Acta Petrologica Sinica， 2017， 33（4）： 11591170.

［9］" 梁世君，羅勸生，康積倫，等．準噶爾盆地吉南凹陷薩探1井風險勘探突破及意義［J］． 中國石油勘探，2021，26（4）：7283．

Liang Shijun， Luo Quansheng， Kang Jilun， et al.Breakthrough and Significance of Risk Exploration in Well Satan 1 in Jinan Sag， Junggar Basin［J］. China Petroleum Exploration， 2021， 26（4）： 7283.

［10］" 張志杰，成大偉，周川閩，等． 準噶爾盆地石樹溝凹陷平地泉組細粒巖特征及其對準東北地區頁巖油勘探的指示意義［J］．天然氣地球科學，2021，32（4）：562576．

Zhang Zhijie， Cheng Dawei， Zhou Chuanmin， et al.Characteristics of Fine-Grained Rocks in the Pingdiquan Formation in Well Shishu 1 and Their Significance for Shale Oil Exploration in Northeastern Junggar Basin［J］. Natural Gas Geoscience， 2021， 32（4）： 562576.

［11］" 匡立春，唐勇，雷德文，等． 準噶爾盆地二疊系咸化湖相云質巖致密油形成條件與勘探潛力［J］． 石油勘探與開發，2012，39（6）：657667．

Kuang Lichun， Tang Yong， Lei Dewen， et al.Formation Conditions and Exploration Potential of Tight Oil in the Permian Saline Lacustrine Dolomitic Rock， Junggar Basin， NW China［J］. Petroleum Exploration and Development， 2012， 39（6）： 657667.

［12］" 王越，于洪州，熊偉，等． 石錢灘凹陷二疊系平地泉組層序沉積特征及石油地質意義［J］． 油氣地質與采收率，2021，28（4）：3545．

Wang Yue， Yu Hongzhou， Xiong Wei， et al.Sequence Sedimentary Characteristics and Petroleum Geological Significance of Permian Pingdiquan Formation in Shiqiantan Sag［J］. Petroleum Geology and Recovery Efficiency， 2021， 28（4）： 3545.

［13］" 劉英輝. 準噶爾盆地烏—夏地區風城組云質巖類沉積環境及成因探討［J］.吉林大學學報（地球科學版）， 2022， 52（1）： 8093.

Liu Yinghui. Origin of Dolomitic Tuff in Permian Fengcheng Formation in Wu-Xia Area of Junggar Basin［J］. Journal of Jilin University （Earth Science Edition）， 2022， 52（1）： 8093.

［14］" 支東明，宋永，何文軍，等． 準噶爾盆地中—下二疊統頁巖油地質特征、資源潛力及勘探方向［J］． 新疆石油地質，2019，40（4）：389401．

Zhi Dongming， Song Yong， He Wenjun， et al. Geological Characteristics， Resource Potential and Exploration Direction of Shale Oil in Middle-Lower Permian， Junggar Basin［J］. Xinjiang Petroleum Geology， 2019， 40（4）： 389401.

［15］" 袁思喬，劉之的，王鼎涵，等．利用多測井參數預測致密砂巖脆性指數方法研究［J］． 地球物理學進展，2022，37（1）：312319．

Yuan Siqiao， Liu Zhidi， Wang Dinghan， et al. Research on Prediction Method of Tight Sandstone Brittleness Index Using Multiple Logging Parameters［J］. Progress in Geophysics， 2022， 37（1）： 312319.

［16］" 付娟娟，郭少斌． 沁水盆地海陸交互相頁巖脆性指數預測與測井響應分析［J］． 石油實驗地質，2019，41（1）：108112．

Fu Juanjuan， Guo Shaobin. Prediction of Brittle Index and Its Relationship with Log Data in Marine-Terrigenous Shale of Qinshui Basin［J］. Petroleum Geology amp; Experiment， 2019， 41（1）： 108112.

［17］" 楊秀春，張繼坤，周科． 鄂東氣田韓城礦區煤層橫波時差測井曲線的構建方法［J］． 測井技術，2014，38（3）：304308．

Yang Xiuchun， Zhang Jikun， Zhou Ke.Study on Establishing Method of Shear Wave Logging Curves for Coalbed in Eastern Block of Ordos Basin［J］. Well Logging Technology， 2014， 38（3）： 304308.

［18］" 孫玉凱，鄭雷清． 基于常規測井資料的橫波時差估算方法及應用［J］． 新疆石油地質，2009，30（4）：521522．

Sun Yukai， Zheng Leiqing. Method for S-Wave Moveout Calculation and Application Based on Conventional Well Logging Information［J］. Xinjiang Petroleum Geology， 2009， 30（4）： 521522.

［19］" 趙炎． 用橫波時差估算裂縫孔隙度方法研究［J］． 新疆石油地質，1984，5（4）：7176．

Zhao Yan. Study on Estimation of Fracture Porosity by Shear Wave Time Difference［J］. Xinjiang Petroleum Geology， 1984， 5（4）： 7176.

［20］" 邵才瑞． 基于巖石物理的多元信息融合方法研究與應用［D］．青島： 中國石油大學（華東），2008．

Shao Cairui. Multi Data Fusion Method Study and Its Application Based on Rock Physics［D］. Qingdao： China University of Petroleum （East China）， 2008.

［21］" Aki K I， Richards P G. Quantitative Seismology-Theory and Method［M］. San Francisco： W H Freeman and Company， 1980.

［22］" 宗兆云，印興耀，張峰，等． 楊氏模量和泊松比反射系數近似方程及疊前反演［J］． 地球物理學報，2012，55（11）：37863794 ．

Zong Zhaoyun， Yin Xingyao， Zhang Feng， et al. Reflection Coefficient Equation and Pre-Stack Seismic Inversion with Young’s Modulus and Poisson Ratio［J］. Chinese Journal of Geophysics， 2012， 55（11）： 37863794.

［23］" 桂金詠，高建虎，雍學善，等． 致密儲層敏感彈性參數疊前同步反演方法［J］． 石油物探， 2015，54（5）：541550．

Gui Jinyong， Gao Jianhu， Yong Xueshan， et al. A Prestack Simultaneous Inversion Method for Sensitive Elastic Parameters of Tight Reservoir［J］. Geophysical Prospecting for Petroleum， 2015， 54（5）： 541550.