最優化理論與方法課程教學創新性體系研究

舒萬能　蹇文成　聶紹良　葛欣

［摘 要］最優化方法是現代管理科學的重要理論基礎和不可缺少的方法，被人們廣泛地應用到計算機科學、智能科學與技術、經濟管理、國防等領域。最優化理論與方法課程是高校人工智能專業一門專業必修課程，為學生熟悉現代最優化理論及方法的設計和應用打下良好的基礎。文章探討了該課程實踐教學的現狀及其存在的問題，分析了該課程目標達成度與實踐教學創新性體系的研究方法與實踐措施。

［關鍵詞］最優化理論與方法；實踐教學體系；計算機科學與技術；人工智能; 精品課程

［中圖分類號］ G642.0 ［文獻標識碼］ A ［文章編號］ 2095-3437（2023）17-0033-03

在人工智能時代，人工智能專業相關課程的實踐教學是培養和提高學生編程能力和創新能力的重要環節。最優化理論與方法課程作為高校人工智能本科專業的一門專業必修課，以數據結構、算法設計與分析等課程為專業基礎，課程的創新性體系研究對培養高素質、創新型、復合型人才有重要的促進作用[1-2]。雖然國內大部分高校人工智能相關的課程開設較早，但人工智能學科成立的時間比較晚，尤其是面向高考招生的人工智能專業，基本上是近五年才開始的。最優化理論與方法作為人工智能專業的核心課程，其實踐教學與創新性體系尚處于起步建設階段，加強實踐教學是實現人才培養目標和提高人才培養質量的迫切要求[3-4]，是實施國內“雙一流”高校建設的內在要求和重要內容。

最優化理論與方法課程主要分析最優化方法在計算機科學、智能科學與技術、經濟管理、國防等領域的作用[5]，研究最優化基本要素和一維最優化方法搜索區間的確定，重點在于分析線性規劃的求解原理和過程，以及整數規劃數學模型和窮舉法，同時設計非線性規劃中的多目標優化模型。通過該課程的學習，學生能夠掌握最優化方法的研究對象、特點，最優化方法模型的建立和模型的分析、求解、應用，線性規劃問題的模型、求解及其應用，動態規劃的模型、求解、應用等內容；掌握最新的智能優化方法和動態規劃，為學生熟悉現代最優化理論及方法的設計和應用打下良好的基礎，以適用人工智能相關事業發展對人才的新要求。

隨著人工智能技術的日漸成熟，尤其是ChatGPT異軍突起，社會各行各業對人工智能專業的關注度日漸高漲，人工智能方向的人才需求與日俱增，研究和探索新時期人工智能專業應用型人才培養模式，培養滿足社會需求的人工智能人才，是我國不斷突破高新技術、解決“卡脖子”技術的重要保障。因此，面向大學生的最優化理論與方法課程實踐教學與創新性體系研究，是人工智能本科專業人才培養勢在必行的課程改革任務。

一、最優化理論與方法課程教學的現狀分析

目前，外國高校的最優化理論與方法課程主要對研究生開設，課程的實踐教學方法主要采用理論聯系實際的教學方法，旨在培養具有創新意識的高素質工程技術人員。國內高校的最優化理論與方法課程在大部分院校開設的學時數為32學時，課程的實踐教學沿用傳統的教學方法，多數實驗是按照具體指導書進行的驗證性實驗，缺乏創新，在實驗過程中很難融入學生自己的思想。

在課堂教學環節，學生要學習的內容較多，而且涉及的知識面比較廣、比較深。分枝定界法和黃金分割法的計算原理雖然比較簡單，但求解過程比較復雜。Hopfield神經網絡、模擬退火算法和遺傳算法這些人工智能算法構思巧妙，但運行機理復雜，運行的時間和空間復雜度較大[6-7]，對于本科生而言，學習難度系數較大，大多數學生對綜合分析題目存在談題色變的情況。在歷屆本科生的期末考試中，該課程的最終考試結果雖然比較理想，但分值分布極不均勻。所以，在新時代教學形勢要求下，實現最優化理論與方法的過程考核機制與實踐教學創新性體系并軌運行，是當前課程教學改革的重要舉措。要以“課程體系化、教材精品化、師資團隊化”的人工智能專業系列課程改革思路為指導，構建以實踐能力、創新能力訓練為特色的課程目標達成度與實踐教學創新性體系。

二、最優化理論與方法課程目標達成度模型設計

最優化理論與方法課程經過不斷改革、完善，探索出了一條提高學生實踐能力和創新能力的新途徑。該課程以掌握整體優化的知識結構為基礎，把實踐教學、創新能力培養貫穿于課程體系設計、落實以及人才培養的全過程，形成行之有效的實踐教學體系。為了準確評價學生的學習效果，全面考核每個學習環節，設計出該課程的課程目標達成度模型。該模型包含課堂測試、平時作業、期中考試和期末考試四個環節，并從目標分值和學生平均得分兩個維度進行評估。

定義1 假設[ai]表示課堂測試的學生平均得分，[bi]表示平時作業的學生平均得分，[ci]表示期中考試的學生平均得分，[di]表示期末考試的學生平均得分，[a*i]表示課堂測試的目標分值，[b*i]表示平時作業的目標分值，[c*i]表示期中考試的目標分值，[d*i]表示期末考試的目標分值，則課程分目標i的達成度可以描述為：

[αi=ai+bi+ci+dia*i+b*i+c*i+d*i]。

定義2 假設[α1]表示課堂測試環節的目標達成度，[α2]表示平時作業環節的目標達成度，[α3]表示期中考試環節的目標達成度，[α4]表示期末考試環節的目標達成度，[β1]表示課堂測試的權重因子，[β2]表示平時作業的權重因子，[β3]表示期中考試的權重因子，[β4]表示期末考試的權重因子，則課程目標達成度可以描述為：

[α=i=14αi×β1， β1+β2+β3+][β4=1]。

三、預期效果與分析

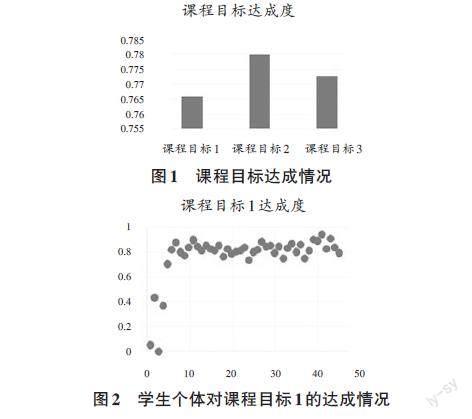
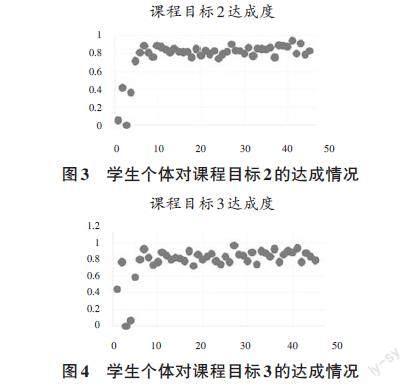
針對該課程教學存在的難點問題，課題組確立了講授和實踐相結合的授課方法，在教學過程中設計三個課程目標：一是掌握最優化基本要素，包括線性規劃數學模型、線性規劃求解基本原理，以及圖搜索算法和人工神經網絡模型；二是掌握常用的求解最優化問題的典型方法和基本原理；三是選用合適的最優化方法，設計系統的多目標數學優化模型，掌握人工智能方法的設計思路和求解過程。以湖北省武漢市某高校人工智能專業2020級某班45位學生為例，該班三個課程目標的達成情況見圖1，學生個體對課程目標1的達成情況見圖2，學生個體對課程目標2的達成情況見圖3，學生個體對課程目標3的達成情況見圖4。[0.785

通過圖1的實驗結果可以看出，通過作業、測驗等進行考核，學生的課程目標達成度為0.766，說明大多數學生能夠達成課程目標，效果較好，學生能夠掌握相關知識并能應用其解決問題。在圖2中，設定目標1里課堂測試的目標分值為30分，平時作業的目標分值為20分，期中考試的目標分值為20分，期末考試的目標分值為35分，最終有4位學生的目標1達成度低于0.6。圖3和圖4的實驗結果顯示，大部分學生的課程目標達成度超過0.6，極少學生計算題得分較低，部分學生的分析題沒有作答導致目標達成度較低。針對上述存在的問題，可以采取以下措施：

第一，以實際最優化問題為導向，結合身邊實際的最優化問題，引導學生思考，充分調動學生學習的積極性、主動性；引導學生深入討論，各抒己見，從而達到發現問題、分析問題、解決問題的目的。

第二，強化學生的自主學習意識。課堂的內容只能作為一種引導，教師應當讓學生掌握自主學習的方法，使學生能夠利用各種資源，特別是網絡資源的優勢自行學習。利用實驗室資源，面向全校學生開展研究性、創新型研究立項，鼓勵學生申報研究課題，為學生提高研究能力創造條件。

第三，開展全方位開放式教學。改革傳統的實踐教學方法和手段，建立以工程能力培養為主線的實踐教學體系與創新能力培養體系。加強與企業合作，校企聯合培訓教師、培養實踐型和創新型人才，提高學生的競爭力。

第四，構建以實踐能力、創新能力訓練為特色的人工智能專業實踐教學體系，改革實踐教學內容、方式和手段，提高教學效果。

四、結語

隨著社會的飛速發展，以科技創新為靈魂的人工智能時代已經來臨。云計算、大數據、物聯網、人工智能等將作為數字經濟的重要技術支撐，為我國高端人才的培養和經濟轉型升級起到舉足輕重的作用。最優化方法已成為現代管理科學的重要理論基礎和不可缺少的方法，被人們廣泛地應用到計算機科學、智能科學與技術、經濟管理、國防等領域，發揮著越來越重要的作用。對于高校而言，產學研相結合促進了課程設置的改革，過程考核與目標達成度并軌，促進了教學方法的變革，能夠提高學生獨立思考和綜合分析問題的能力，同時逐步培養大學生的科研意識。本文提出的最優化理論與方法課程目標達成度與實踐教學創新性體系的構建，經教學實踐的檢驗，具有較好的應用效果。在今后的實踐教學過程中，課程組將進一步對教學內容、教學工具和教學方式進行研究和探討，使其為最優化理論與方法課程的教學構建更有力的支撐平臺。

［ 參 考 文 獻 ］

[1] 黃平，孟永鋼.最優化理論與方法[M].北京：清華大學出版社，2009.

[2] 傅英定，成孝予，唐應輝.最優化理論與方法[M].北京：國防工業出版社，2008.

[3] 袁亞湘，孫文瑜.最優化理論與方法[M].北京：科學出版社，1997.

[4] 施光燕，錢偉懿，龐麗萍.最優化方法[M].北京：高等教育出版社，2007.

[5] 孫文瑜，徐成賢，朱德通.最優化方法[M].2版.北京：高等教育出版社，2010.

[6] SHU W N，CAI K，XIONG N N.Research on strong agile response task scheduling optimization enhancement with optimal resource usage in green cloud computing[J].Future generation computer systems，2021（124）：12-20.

[7] SHU W N，CAI K，XIONG N N.A short?term traffic flow prediction model based on an improved gate recurrent unit neural network[J].IEEE transactions on intelligent transportation systems，2022，23（9）：16654-16665.

［責任編輯：黃緊德］