負必然-可能半三支概念及其應用

王啟君, 林藝東*, 林宇靜, 林夢雷,2

（1.閩南師范大學數學與統計學院,福建 漳州 363000；2.閩南師范大學數字福建氣象大數據研究所,福建 漳州 363000）

形式概念分析（formal concept analysis，FCA）作為一種從形式背景進行數據分析和規則提取的強有力工具，由德國數學家Wille[1-2]于1982年提出.形式概念分析通過對本體的概念、屬性、關系等用形式化的語境表述出來，生成形為（外延、內涵）二元對的形式概念，并利用伽羅瓦連接構造出概念格（Concept lattice）.目前FCA 的主要研究方向有屬性約簡、規則提取、三支概念分析和網絡形式背景等[3-12].同時該理論已成功應用于博客數據分析、智慧城市等領域[13-16].

三支概念分析(three-way concept analysis,3WCA)是將三支決策理論[17]與FCA 相結合產生的一種知識發現理論[8-10].受三個論域范疇的啟發，它基于對概念的二元理解，把FCA 擴展到三元情況[18]，因此很多FCA中的研究內容可平移到3WCA中，如：三支概念格構建和約簡[19-24]、三支概念學習[25-27]以及模糊三支概念分析[26,28]等.同時3WCA也在沖突分析、醫療診斷等方面得到成功應用[29-31].

三支概念從共性角度對對象和屬性進行三分，由于在某些實際情況中共性信息可能不那么重要，魏玲等[32]結合必然算子與可能算子提出必然-可能半三支概念，將單向對應思想引入3WCA，可以應用于團隊合作問題，拓寬概念的語義.然而在教育教學中，老師不僅關心怎樣能讓小組合作達到最佳效果，還需要關注學生不會解決的問題便于教師及時采取措施以改善學生的學習狀態，這就使得考慮負背景下的信息成為必要.基于此問題，提出負必然、負可能算子，并結合區間集[33]，定義負必然-可能半三支概念，進而生成負必然-可能半三支概念格，最后用教育教學中的實例說明該理論的實用性.

1 基礎知識

本節給出三支概念分析的一些基礎知識.

對于任意非空論域U，若P(U)為其冪集，令DP(U)=P(U)×P(U).

U上的區間集為

記U上所有的區間集記為IP(U).

定義1[2]設三元組(G,M,I)為一個形式背景，其中：G={g1,g2,…，gp}為對象集；M={m1,m2,…,mq}為屬性集.I?G×M，若(g,m)∈I，則稱對象g具有屬性m.

對于任意X?G和A?M，定義算子*與算子為

其中：Ic=G×M-I.

特別地，對于任意的g∈G,m∈M，記{g}*為g*，{m}*為m*.

一些學者從模態邏輯的角度，將*算子稱為充分算子，并陸續提出必然算子、可能算子以及對偶充分算子等概念[34-35].

給定形式背景(G,M,I)，對于任意X?G，A?M，必然算子□定義為

可能算子?定義為

定義2[32]設(G,M,I)為一個形式背景，對于任意X∈P(G)，定義對象導出必然-可能三支算子?：，X?=[X□,X?]，簡稱ONPE-算子.

定義3[32]設(G,M,I)為一個形式背景，對于任意若則稱為對象導出必然-可能半三支概念，簡稱為ONPSE-概念，

其中X稱為ONPSE-概念的外延，稱為ONPSE-概念的內涵.

定義4[32]設(G,M,I)為一個形式背景，對于任意A∈P(M)，定義屬性導出必然-可能三支算子?：P(M)→IP(G)，A?=[A□,A?]，簡稱ANPE-算子.

定義5[32]設(G,M,I)為一個形式背景，對于任意若，則稱為屬性導出必然-可能半三支概念，簡稱為ANPE-概念，

2 基于負信息的對象導出必然-可能半三支概念

上述提出的必然-可能半三支概念是基于正背景的角度，關注的是怎樣合作使得團隊更高效高質量地完成工作，而在教育教學中教師不僅需要關注學生已經掌握的知識點，也需關注學生不會解決的問題.這就需要利用負信息從另一方面對對象集、屬性集的信息進行刻畫.

2.1 對象導出負必然-可能三支算子

定義6給定形式背景(G,M,I)，對于任意X?G,A?M，負必然算子定義為

性質1設(G,M,I)為一個形式背景，對于任意X,X1,X2∈G,A,A1,A2∈M,有

證明(i)對?a∈，有?X，即∩X=≠?，則a∈，故Xˉ?.同理可證Aˉ?.

(ii)對?a∈，有?X1，又X1?X2，有a-*?X2，則a∈，所以?.故當X1?X2時?.同理可證A1?A2??.(iii)對?a∈，有∩X1≠?，又X1?X2，有∩X2≠?，則a∈，所以?.故當X1?X2時有?.同理可證A1?A2??.

例1表1為形式背景(G,M,I)，其中對象集G={1,2,3,4}代表四名學生，屬性集M={a,b,c,d}代表學生在學習過程中需要解決的問題.表1 中“1”表示學生會解決此問題，“0”則表示學生不會解決此問題，如：學生1會解決的問題有a,c,d,不會解決的問題為b.

表1 形式背景(G,M,I)Tab.1 Formal context (G,M,I)

定義7設(G,M,I)為一個形式背景，對于任意X∈P(G)，定義對象導出負必然-可能三支算子：P(G)→IP(M)，，簡稱NONPE-算子.

NONPE-算子具有以下性質：

性質2設(G,M,I)為一個形式背景，對于任意X1,X2∈P(G)，有

證明(i)若X1?X2，由性質1(ii) ～(iii)，有，則

2.2 對象導出負必然-可能半三支概念

定義8設(G,M,I)為一個形式背景，對于任意X∈P(G)，，若，則稱為對象導出負必然-可能半三支概念，簡稱為NONPSE-概念，其中X為NONPSE-概念的外延，為NONPSE-概念的內涵.

對于對象子集X?G，NONPE-算子可以同時獲取必然屬性與可能屬性，并形成屬性集M上的一個區間集，這個區間集可將M分為3 部分：正域POSX=、負域NEGX=M-以及邊界域并且POSX、NEGX和BNDX兩兩互不相交，形成M的一個弱三劃分.

例2表1形式背景下所有的概念如表2所示.

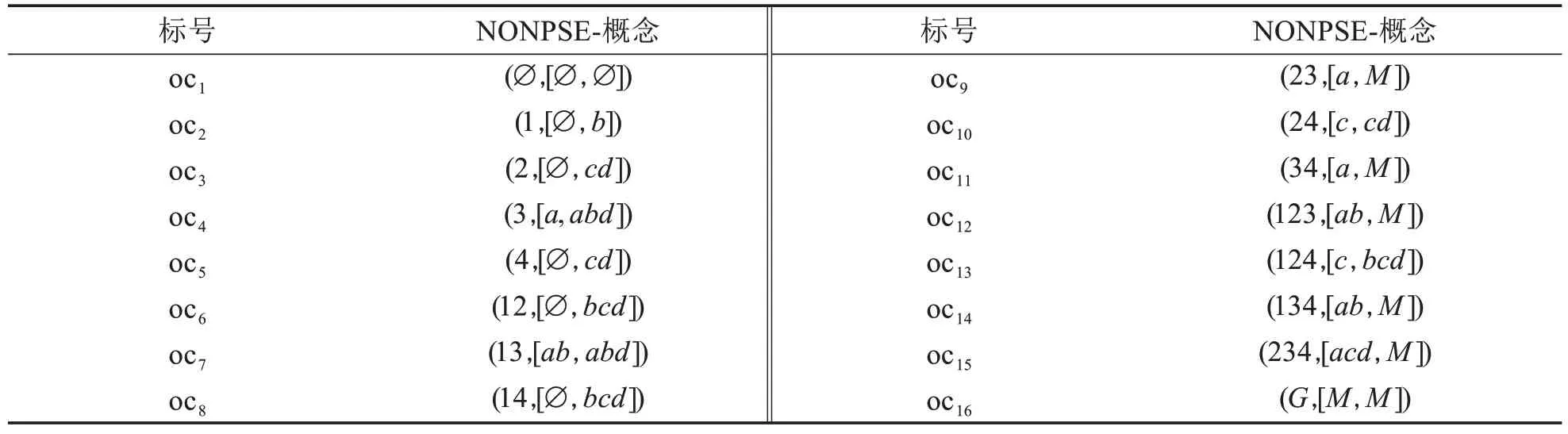
表2 表1 的NONPSE-概念Tab.2 NONPSE-concept of Table1

以概念(23,[a,M])， (34,[a,M])為例解釋NONPSE-概念的語義.概念(23,[a,M])表明：不會解決問題a的學生一定在2 和3 中，且學生2 和3 不會解決的問題在M中；概念(34,[a,M])表明：不會解決問題a的學生一定在3和4中，且學生3和4不會解決的問題在M中，進一步可以說明，學生3一定不會解決問題a，也符合概念(3,[a,abd])的語義.

記(G,M,I)的所有NONPSE-概念的集合為NONPSEL(G,M,I)，定義其偏序關系為：對于任意

稱NONPSEL(G,M,I)為(G,M,I)的對象導出負必然-可能半三支概念格，簡稱為NONPSE-概念格.定理1給出其上、下確界，并證明其是一個完備格.

定理1NONPSEL(G,M,I)是一個完備格，其上、下確界分別為

證明對于任意的由NONPE-算子的定義可知

則X1?X且X2?X，故X1∪X2?X，因此

定理2ONPSEL(G,M,I)?NONPSEL(G,M,I).

證明記 ONPSEL(G,M,I)=L(G,M1,I1)，NONPSEL(G,M,I)=L(G,M2,I2)，對任意，總存在使得X′=X，則L(G,M1,I1)≤L(G,M2,I2)；又對任意總存在使得X=X′,則L(G,M2,I2)≤L(G,M1,I1)，故L(G,M1,I1)?L(G,M2,I2)，即ONPSEL(G,M,I)?NONPSEL(G,M,I).

例3表1的NONPSE-概念格如圖1所示.

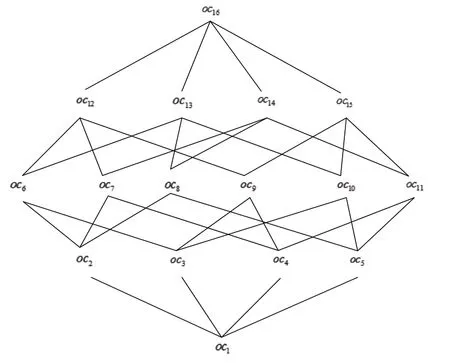
圖1 表1的NONPSE-概念格Fig.1 NONPSE-concept lattice of Table1

由NONPSE-概念定義可知，任給一個對象子集X?G，都存在一個NONPSE-概念(X,[,])與之一一對應.

3 基于負信息的屬性導出必然-可能半三支概念

3.1 屬性導出負必然-可能三支算子

定義9設(G,M,I)為一個形式背景，對于任意A∈P(M)，定義屬性導出負必然-可能三支算子，簡稱NANPE-算子.

NANPE-算子有以下性質.

性質3設(G,M,I)為一個形式背景，對于任意A1,A2∈P(M)，有

3.2 屬性導出負必然-可能半三支概念

定義10設(G,M,I)為一個形式背景，對于任意，則稱為屬性導出負必然-可能半三支概念，簡稱為NANPSE-概念，

NONPSE-概念與NANPSE-概念統稱為負必然-可能半三支概念，簡稱為NANPSE-概念.

類似于NANPSE-算子，對于屬性子集A?M，可以利用NANPSE-算子獲得對象集G上的一個區間集這個區間集可將G分為3 部分：正域、負域，及邊界域，并形成G的一個弱三劃分.

記(G,M,I)的所有NANPSE-概念的集合為NANPSEL(G,M,I),定義其偏序關系為：對于任意

稱NANPSEL(G,M,I)為(G,M,I)的屬性導出負必然-可能半三支概念格，簡稱為NANPSE-概念格.定理2給出其上、下確界，證明同定理1，這里不再贅述.

定理3NANPSEL(G,M,I)是一個完備格，其上、下確界分別為

定理4ANPSEL(G,M,I)?NANPSEL(G,M,I).

例4表1形式背景下所有的NANPSE-概念如表3所示，NANPSE-概念格如圖2所示.

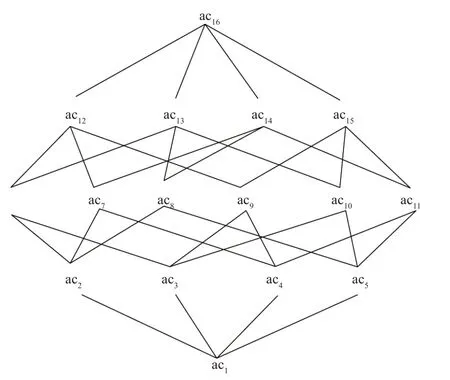
圖2 表1的NANPSE-概念格Fig.2 NANPSE-concept lattice of table 1

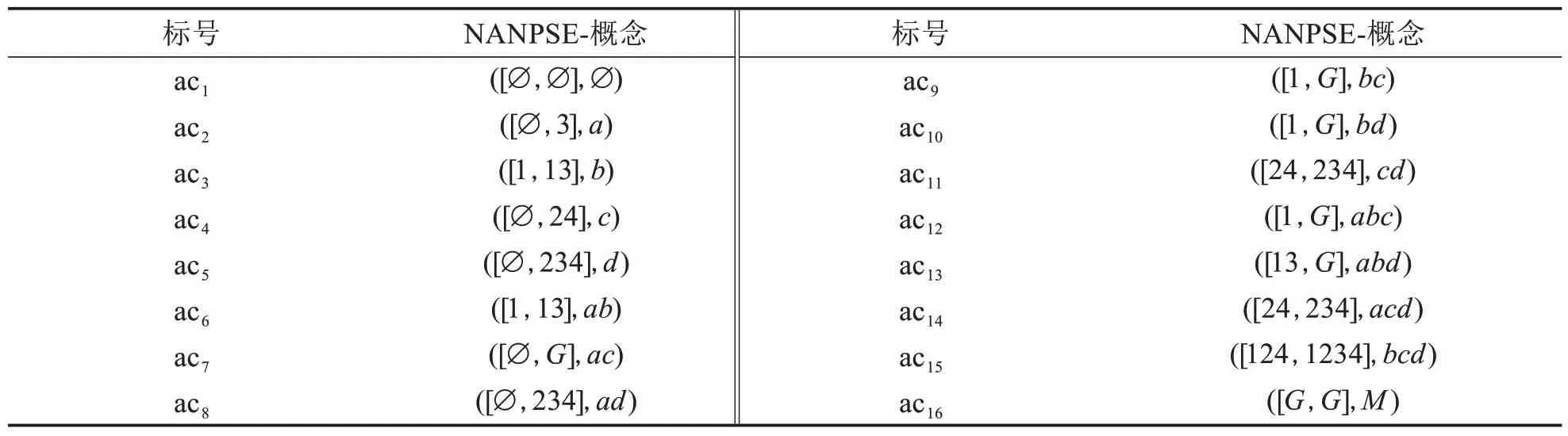
表3 表1 的NANPSE-概念Tab.3 NANPSE-concept of table 1

以概念([1,G],bc), ([1,G],bd)為例解釋NANPSE-概念的語義.概念([1,G],bc)表明：學生1 一定不會解決問題b或c，且不會解決問題b和c的學生可能在G中；概念([1,G],bd)表明：學生1一定不會解決問題b或d，且不會解決問題b和d的學生可能在G中，進一步可以說明，學生1 一定不會解決問題b，也符合概念([1,13],b)的語義；另一方面，，可以看出，即不會問題c的同學一定不會d，故概念([1,G],bc)， ([1,G],bd)內涵不同外延卻一致.

4 例子

在第二、三節定義負必然-可能三支半概念，它既能對數據信息進行有效表述又避免經典形式概念下由于強對應關系造成的信息丟失.為說明所提出負必然-可能三支半概念的實用性，在某小學四年級隨機挑選20名學生進行案例分析，通過測試題的形式對他們解決問題的能力進行檢驗，其中測試題目為：a.計算；d.解方程；e.一個數的比它的多60，求這個數.具體測試結果如表4，學生正確解決該問題記為1，否則為0.

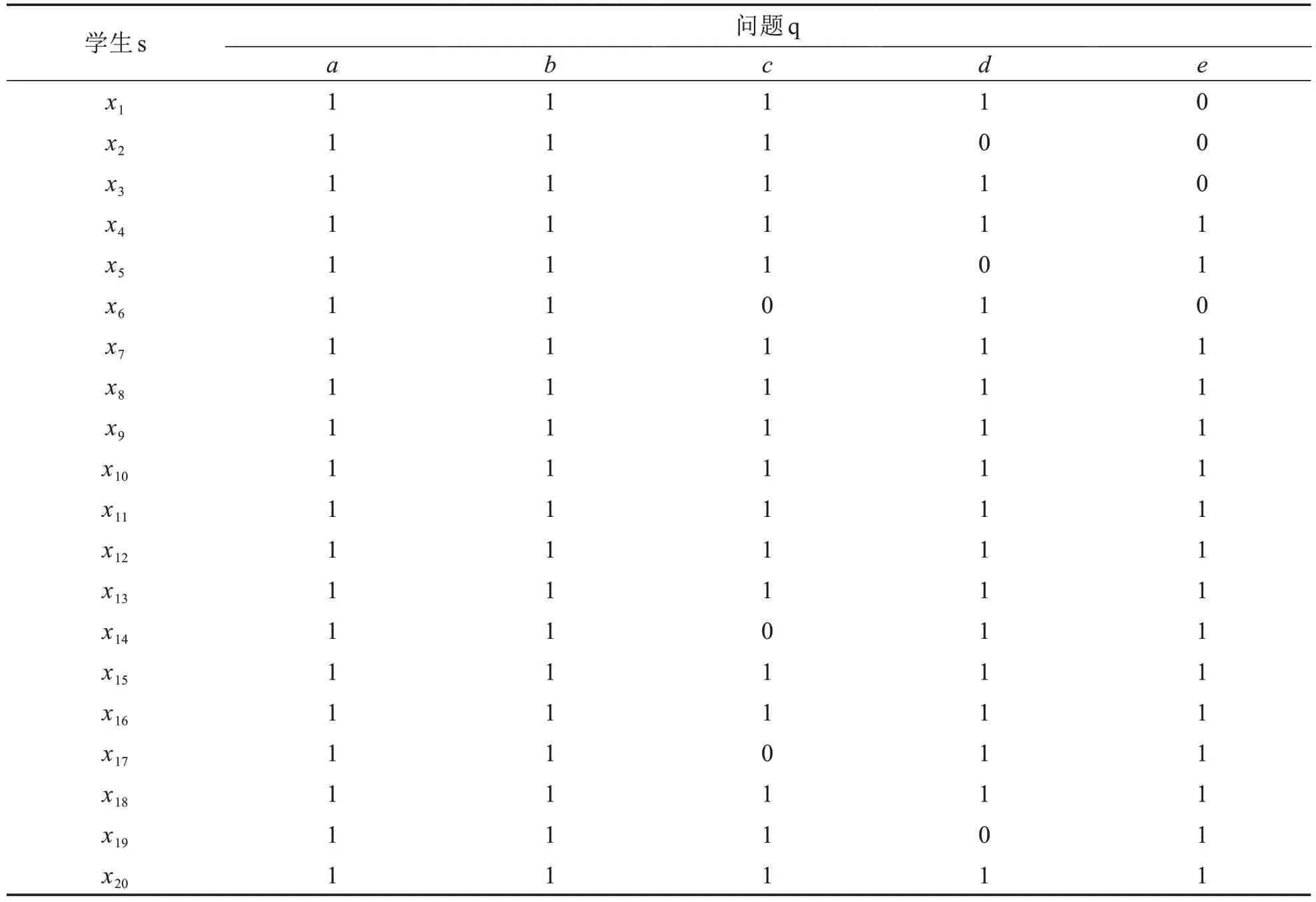
表4 測試結果Tab.4 Test result

由于學生全部做對和全部做錯在的研究中不具有參考價值，故刪去全部正確、全部錯誤的數據，由于存在相同測試結果，為表示簡便，令[x1]q={x1,x3}，[x2]q={x2}，[x5]q={x5,x19}，[x6]q={x6}，[x14]q={x14,x17}，最終處理后的測試結果所產生的形式背景如表5～6 所示，其中“1”表示學生會解決此問題，“0”則表示學生不會解決此問題.

表5 形式背景(G,M,I)Tab.5 An formal context (G,M,I)

表6 表5 的NONPSE-概念Tab.6 NONPSE-concept of Table5

受粗糙集思想的啟發，每一個NONPSE-概念的內涵都可以看成由正域POSX=、負域NEGX=M-組成的區間，而對于某個問題而言，教師在教學過程中更容易關注到學生不確定掌握的問題，即邊界問題，那么這些問題是否需要進一步講解就成為教師需要關注的方向，故引入問題判別參數（q-discriminant parameter）dαq的定義.

定義11設為NONPSE-概念，其邊界問題為，對任意問題m∈M，其判別參數dαq為

其中：|oc|為所有NONPSE-概念的個數，|X|為概念外延所含對象個數，如概念oc7：([x1]q[x2]q,[?,de])其外延所含對象個數，若dαq≥α則說明問題需要被老師關注，采取進一步的措施解決該問題.

在案例中，令α=0.5，dαq(c)=0.47 ＞α，dαq(d)=0.58 ≥α，dαq(e)=0.72 ＞α，即問題d,e 存在一定難度，學生不能順利解決該問題，需要教師采取進一步措施.問題與其判別參數的變化趨勢如圖3所示.

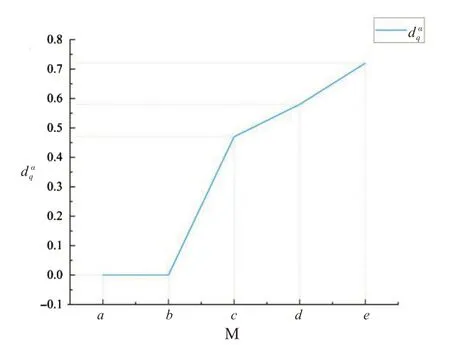
圖3 問題判別參數d αqFig.3 Discriminant parameter of question d αq

圖3 分析：由圖中可以看出，dαq(d),dαq(e)＞α，即問題d,e需要被教師進一步解決.從知識層面來說，數學學科知識量大且語言抽象，思維方法具有層次性躍遷，會出現一個知識點講授很多遍，學生不會做題的情況.故而，針對這些仍然存在困惑的問題就急需教師采取不同措施解決.

針對問題d，dαq(d)=0.58 ≥α，只有一部分同學對該問題存有困惑，并不需要在全班進行講解，可以針對該問題制作微課上傳至云平臺，供學生自助取用；針對問題e，可以看出該問題的相關知識點學生掌握程度較低，可以對全班同學進行精準知識講解，力求突破難點.根據布魯姆的掌握學習理論的核心觀點：若給足學生時間并采取適當的教學方法，幾乎每個學生可以對所有內容達到掌握的程度.通過精準有針對性的輔導，不僅可以高效解決數據反饋的問題，而且能夠針對具體問題采取強化措施，見表7.

表7 表5的NANPSE-概念Tab.7 NANPSE-concept of Table 5

而對于學生而言問題可以反應該學生對知識的理解程度，每一個NANPSE-概念的內涵都可以看成由POSA=、負域NEGA=G-組成的區間，教師在教學過程中應該注意到對某些問題似是而非的同學，即處于邊界域的學生，為確定這些學生是否需要教師個性化輔導，故引入對于學生的判別參數（s-discriminant parameter）dβs的定義.

定義12設為NANPSE-概念，，對任意學生[xj]q∈G，其判別參數為

在案例中，令β=0.4，dβs([x1]q)=0，dβs([x2]q)=0.44，dβs([x5]q)=0.11，dβs([x6]q)=0.33，dβs([x14]q)=0，可以看出學生2需要教師進一步輔導.然而，學生是具有個體差異性的，個性化輔導便是彌補上述情況的有效手段.如：學生2對知識點的理解不夠透徹，可以考慮進行課后作業輔導、精準考后分析等措施，做出適當的調整和補救，這樣可以使得個性化輔導更有針對性，從而改善學困生的學習狀態，與此同時，dβs([x2]q)＞dsβ([x6]q)＞dsβ([x5]q)，即學生2急需老師關注，學生6，5，19次之，教師采用個性化輔導也可加強師生之間的聯系，使老師得到及時的反饋，增強學生的幸福感.

目前，對于學困生的教育效果直接影響素質教育的深化及新課程改革目標的實現，導致對學困生教育的關注度越來越高，因此教師需在教學實踐和日常生活中對這類學生因材施教，以推動素質教育的進一步發展.

5 結論

在教育教學中的實際背景下，結合區間集，定義負必然-可能半三支概念，從負背景上拓寬半三支概念的語義.而對象和屬性作為兩種不同的研究角度，生成的兩種負必然-可能半三支概念應用場景也有所不同，對象導出負必然-可能半三支概念從對象出發，對屬性進行劃分，屬性導出負必然-可能半三支概念從屬性出發，對對象進行劃分，因此如何結合上述研究成果，對負必然-可能半三支概念的應用做進一步研究也很有意義.同時必然算子與可能算子與粗糙集的上、下近似密切相關，故如何將其與粗糙集理論相結合也很有必要.在概念認知學習中，通過概念對事物進行認知也是一個值得研究的課題，由于負必然-可能半三支概念的外延與內涵沒有嚴苛的雙向對應，能否能在概念認知學習過程中取得較好的效果也值得討論.這些都是未來的研究方向.