圖的全局意大利控制數

郝國亮,吳愉琪,曾淑婷

(1.東華理工大學理學院,江西 南昌 330013;2.菏澤學院數學與統計學院,山東 菏澤 274015)

1 預備知識

近幾十年來,基于不同的應用背景,圖的控制參數問題得到了廣泛研究.[1-2]1999年,Stewart[3]提出了君士坦丁大帝時期防御羅馬帝國的策略“Defend the Roman Empire”.基于該策略,Cockayne等[4]引入了圖的羅馬控制的概念.2016年,Chellali等[5]將“Defend the Roman Empire”中的防御策略弱化,提出了圖的羅馬{2}-控制數的概念.隨后,羅馬{2}-控制被Henning等[6]重新命名為意大利控制.Gao等[7]計算了笛卡爾乘積圖的意大利控制數的精確值.Varghese等[8]研究了邊的增加對意大利控制數的影響.Banerjee等[9]給出了計算余圖的完美意大利控制數的線性時間算法.本文將研究圖的全局意大利控制問題,給出了一般圖的全局意大利控制數的界并且得到了某些特殊圖的全局意大利控制數的精確值.

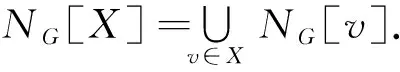
2 主要結論及其證明

命題1 對任意n階圖G,min{n,4}≤γgI(G)≤n.

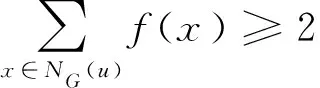
由于0

證明當n∈{3,4}時,由命題1知,γgI(Fn)=n.設n≥5且設扇形圖Fn是由路Pn-1=v2v3…vn和一個不在路Pn-1上的頂點v1組成,且使得v1與其他頂點都相鄰.

若5≤n≤10,由命題1,要證明γgI(Fn)=4成立,只需要證明γgI(Fn)≤4即可.如果n=5,則定義F5的全局意大利控制函數g使得g(v5)=0,且當i≠5時g(vi)=1,于是γgI(F5)≤ω(g)=4;如果n∈{6,7},則定義Fn的全局意大利控制函數g使得當i∈{1,2,5,6}時g(vi)=1,且當i?{1,2,5,6}時g(vi)=0,于是γgI(Fn)≤ω(g)=4;如果n∈{8,9},則定義Fn的全局意大利控制函數g使得當i∈{1,2,5,8}時g(vi)=1,且當i?{1,2,5,8}時g(vi)=0,于是γgI(Fn)≤ω(g)=4;如果n=10,則定義F10的全局意大利控制函數g使得當i∈{1,3,6,9}時g(vi)=1,且當i?{1,3,6,9}時g(vi)=0,于是γgI(F10)≤ω(g)=4.

若n≥11,定義Fn的全局意大利控制函數g使得g(v1)=g(v2)=2,g(v3)=1且當i?{1,2,3}時,g(vi)=0,故γgI(Fn)≤5.往證γgI(Fn)≥5.由命題1,只要證明γgI(Fn)≠4即可.反證法.假設γgI(Fn)=4,令f是γgI(Fn)-函數,則ω(f)=γgI(Fn)=4.

斷言1f(v1)=1.

這與f是γgI(Fn)-函數矛盾.因此f(v1)=1.斷言1得證.

斷言2f(vi-1)+f(vi)+f(vi+1)≥1,其中3≤i≤n-1.

事實上,若結論不真,則存在3≤i≤n-1使得f(vi-1)=f(vi)=f(vi+1)=0.則由斷言1知,

這與f是γgI(Fn)-函數矛盾.斷言2得證.

因為n≥11,所以由斷言1和斷言2可得

易見上式中“=”成立.因此f(v2)=f(vn)=0.又因為f(v1)=1,所以由γgI(Fn)-函數的定義知,f(v3)≥1且f(vn-1)≥1.因此由斷言1和2知,

矛盾.于是當n≥11時,γgI(Fn)≠4.

證明當n∈{3,4}時,由命題1知,γgI(Wn)=n.下設n≥5且設輪圖Wn是由圈Cn-1=v2v3…vnv2和一個不在圈上的頂點v1組成,且使得v1與其他頂點都相鄰.

假設n∈{6,8,10}.由命題1,要證明γgI(Wn)=4成立,只需證明γgI(Wn)≤4即可.如果n=6,則定義W6的全局意大利控制函數g使得當i∈{2,3}時g(vi)=0,且當i?{2,3}時g(vi)=1,于是γgI(W6)≤ω(g)=4;如果n∈{8,10},則定義Wn的全局意大利控制函數g使得當i∈{1,2,5,8}時g(vi)=1,且當i?{1,2,5,8}時g(vi)=0,于是γgI(Wn)≤ω(g)=4.

假設n∈{5,7,9}或n≥11.定義W5的全局意大利控制函數g使得對任意i∈{1,2,3,4,5},g(vi)=1,于是γgI(W5)≤ω(g)=5.當n∈{7,9}或n≥11時,定義Wn的全局意大利控制函數g使得g(v1)=2,當i∈{2,3,4} 時g(vi)=1,且當i?{1,2,3,4} 時g(vi)=0,于是γgI(Wn)≤ω(g)=5.接下來證明:當n∈{5,7,9}或n≥11時,γgI(Wn)≥5.由命題1,只需要證明γgI(Wn)≠4.用反證法.假設γgI(Wn)=4,令f是γgI(Wn)-函數,則ω(f)=γgI(Wn)=4.

斷言1f(v1)=1且對任意i∈{2,3,…,n},f(vi)∈{0,1}.

事實上,類似于定理2中斷言1 的證明可得f(v1)=1.往證對任意i∈{2,3,…,n},f(vi)∈{0,1}.用反證法.不失一般性,若f(v2)?{0,1},則顯然f(v2)=2.于是

因此f(v3)和f(vn)中至少一個為0,不妨假設f(v3)=0,于是

這與f是γgI(Wn)-函數矛盾.因此對任意i∈{2,3,…,n},f(vi)∈{0,1}.斷言1得證.

類似于定理2 中斷言2 的證明可得如下斷言:

斷言2f(vi)+f(vj)+f(vk)≥1,其中2≤i,j,k≤n且NWn(vj)-{v1}={vi,vk}.

斷言3 不存在3個頂點vi,vj和vk使得f(vi)=f(vk)=1且f(vj)=0,其中2≤i,j,k≤n且NWn(vj)-{v1}={vi,vk}.

事實上,若結論不真,不失一般性,假設f(v2)=f(v4)=1且f(v3)=0.又因為f(v1)=1,所以

這與f是γgI(Wn)-函數矛盾.于是斷言3得證.

與假設γgI(Wn)=4矛盾.

綜上所述,對任意n∈{5,7,9}或n≥11,γgI(Wn)≠4.