基于HRFDE和GSA-PNN的旋轉(zhuǎn)機(jī)械故障識別模型*

赫大雨,王 強(qiáng)

(1.吉林鐵道職業(yè)技術(shù)學(xué)院 鐵道機(jī)車學(xué)院,吉林 吉林 132299;2.東南大學(xué) 機(jī)械工程學(xué)院,江蘇 南京 210096)

0 引 言

旋轉(zhuǎn)機(jī)械是較為常見的機(jī)械設(shè)備,研究針對旋轉(zhuǎn)機(jī)械的故障診斷方法對確保設(shè)備平穩(wěn)安全地運行具有重要意義[1-2]。

旋轉(zhuǎn)機(jī)械在發(fā)生故障后,振動信號中將出現(xiàn)之前不存在的沖擊成分和諧波分量,使得信號的復(fù)雜性發(fā)生突變。因此,通過對旋轉(zhuǎn)機(jī)械的振動信號進(jìn)行分析,以此來檢測設(shè)備的故障是一種行之有效的方法[3]。但是由于該振動信號呈現(xiàn)出復(fù)雜的非線性和非平穩(wěn)性,因此,在針對旋轉(zhuǎn)機(jī)械的故障診斷中,非線性動力學(xué)分析方法的應(yīng)用非常廣泛。非線性動力學(xué)分析方法以樣本熵[4]、排列熵[5]、模糊熵[6]、散布熵[7]和多尺度散布熵(multiscale dispersion entropy,MDE)[8]為代表。

MDE具有計算效率高、特征提取能力強(qiáng)等優(yōu)點。喬新勇等人[9]將MDE用于柴油機(jī)的故障診斷,結(jié)果表明,MDE在故障診斷中具有有效性;然而MDE的粗粒化處理只考慮了時間序列的低頻特征,而忽略了高頻特征中的故障信息。隨后,柯赟等人[10]基于層次熵和散布熵,提出了層次散布熵(HDE),借此全面地提取到了信號中的故障特征,并對噴油器故障進(jìn)行了精準(zhǔn)識別;然而HDE只考慮了信號幅值的絕對性而忽略了相對性,無法有效地評估信號的波動性。隨后,KE Yun等人[11]充分考慮了信號的波動性,提出了層次波動散布熵(hierarchical fluctuation dispersion entropy,HFDE),并將其用于噴油器的故障診斷,有效地提取了其故障特征;然而HFDE無法提取信號的深層次信息,其特征提取的效果還有待提升。

為了進(jìn)一步提高HFDE的特征提取性能,JIAO Shang-bin等人[12]提出了反向波動散布熵(reverse fluctuation dispersion entropy,RFDE),該方法在故障特征提取過程中,同時考慮了波動散布熵的幅值、波動信息和反向排列熵的距離信息,而基于該方法的齒輪故障信號識別結(jié)果也證明了RFDE的有效性;然而RFDE無法進(jìn)行信號的多尺度分析。為此,宋來建等人[13]127-128和周經(jīng)龍等人[14]分別提出了時移多尺度反向波動散布熵和精細(xì)復(fù)合多尺度反向波動散布熵,并將它們分別應(yīng)用于旋轉(zhuǎn)機(jī)械和滾動軸承的故障診斷,結(jié)果也驗證了反向波動散布熵的有效性;然而,上述2種方法雖然實現(xiàn)了信號的深層次特征提取目的,但由于所采用的粗粒化處理方法的固有缺陷,其無法提取信號高頻特征中的故障信息。

在模式識別方面,由于具有較快的收斂速度以及較強(qiáng)的處理非線性數(shù)據(jù)的能力,概率神經(jīng)網(wǎng)絡(luò)(PNN)被廣泛應(yīng)用于故障的診斷領(lǐng)域。但是其性能易受到平滑因子設(shè)置的影響,造成故障分類結(jié)果的不穩(wěn)定。為此,劉福政等人[15]采用粒子群算法(particle swarm optimization,PSO)對PNN的平滑因子進(jìn)行了搜索,建立了參數(shù)最優(yōu)的PNN分類模型,并將其用于滾動軸承的故障識別,結(jié)果驗證了該分類器的有效性;但是PSO易陷入局部最優(yōu)。黨建等人[16]采用螢火蟲算法對PNN進(jìn)行了優(yōu)化,對回轉(zhuǎn)窯的故障進(jìn)行了有效識別;但螢火蟲算法的全局優(yōu)化性能依然不足。因此,迫切需要采用具有良好全局優(yōu)化性能和局部優(yōu)化性能的算法對PNN進(jìn)行優(yōu)化,以構(gòu)建網(wǎng)絡(luò)參數(shù)最優(yōu)的PNN分類模型。

針對上述問題,為了從振動信號中提取出更高質(zhì)量的故障特征,以及準(zhǔn)確判斷旋轉(zhuǎn)機(jī)械的故障類型,筆者提出層次反向波動散布熵(HRFDE)方法,并將其用于提取旋轉(zhuǎn)機(jī)械的故障特征,實現(xiàn)深層次故障特征的提取目的。

基于此,筆者將HRFDE用于提取旋轉(zhuǎn)機(jī)械的故障特征,并采用引力搜索算法(GSA)優(yōu)化PNN,在此基礎(chǔ)上提出一種基于HRFDE和GSA-PNN的旋轉(zhuǎn)機(jī)械故障診斷方法。

首先,利用HRFDE提取旋轉(zhuǎn)機(jī)械的故障特征,以準(zhǔn)確表征旋轉(zhuǎn)機(jī)械的不同故障狀態(tài);隨后,采用引力搜索算法對概率神經(jīng)網(wǎng)絡(luò)進(jìn)行優(yōu)化,構(gòu)建網(wǎng)絡(luò)參數(shù)最優(yōu)的分類器,并進(jìn)行訓(xùn)練;最后,利用訓(xùn)練好的分類器對故障樣本進(jìn)行識別,并基于滾動軸承和齒輪箱兩組故障數(shù)據(jù)進(jìn)行實驗分析。

1 層次反向波動散布熵

1.1 多尺度反向波動散布熵

宋來建等人[13]126-127基于多尺度分析和反向波動散布熵的概念,提出了多尺度反向波動散布熵(MRFDE),并將其用于旋轉(zhuǎn)機(jī)械的故障特征提取。

MRFDE的理論原理如下:

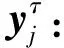
(1)

式中:τ為尺度因子,τ=1,2,…,n。

2)計算每個粗粒向量的RFDE,得到n個粗粒向量的RFDE值,將其表示為尺度因子τ的函數(shù),稱為MRFDE分析,其表達(dá)式如下:

(2)

綜上可以發(fā)現(xiàn),MRFDE將原始信號分割為多個子序列,進(jìn)而從多個尺度測量信號的復(fù)雜度。然而,MRFDE所采用的粗粒化處理是對數(shù)據(jù)取平均的過程,其只提取了信號的低頻成分,遺漏了高頻成分。

1.2 層次反向波動散布熵

為了實現(xiàn)信號的高頻分量分析目的,筆者基于層次分割對信號進(jìn)行處理,提出了層次反向波動散布熵(HRFDE)。相較于MRFDE,HRFDE既能夠?qū)崿F(xiàn)信號的多尺度分析目標(biāo),也能夠有效提取信號的低頻和高頻分量。

HRFDE的計算過程如下:

1)對于長度N的信號{u(i),i=1,2,…,N},給定平均算子Q0和差分算子Q1為:

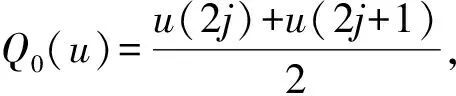
(3)

其中:N=2n;算子Q0和算子Q1的長度為2n-1。

根據(jù)算子Q0和Q1,原信號可以重構(gòu)為:

u={(Q0(u)j+Q1(u)j),(Q0(u)j-Q1(u)j)}

(4)

當(dāng)j=0或j=1時,矩陣Qj定義如下:

Qj(u)=

(5)

2)構(gòu)造n維向量[γ1,γ2,…,γn]∈{0,1},則整數(shù)e可以定義為:

(6)

式中:e為對應(yīng)向量[γ1,γ2,…,γn];

3)基于向量[γ1,γ2,…,γn],定義信號u(i)每一層分解的節(jié)點分量為:

uk,e=Qγn·Qγn-1·…·Qγ1(u)

(7)

式中:k為層次分析中的第k層。

原始信號u(i)在第k+1層的低頻分量和高頻分量分別由uk,0和uk,1表示。

信號u(i)的層次分解示意圖如圖1所示。

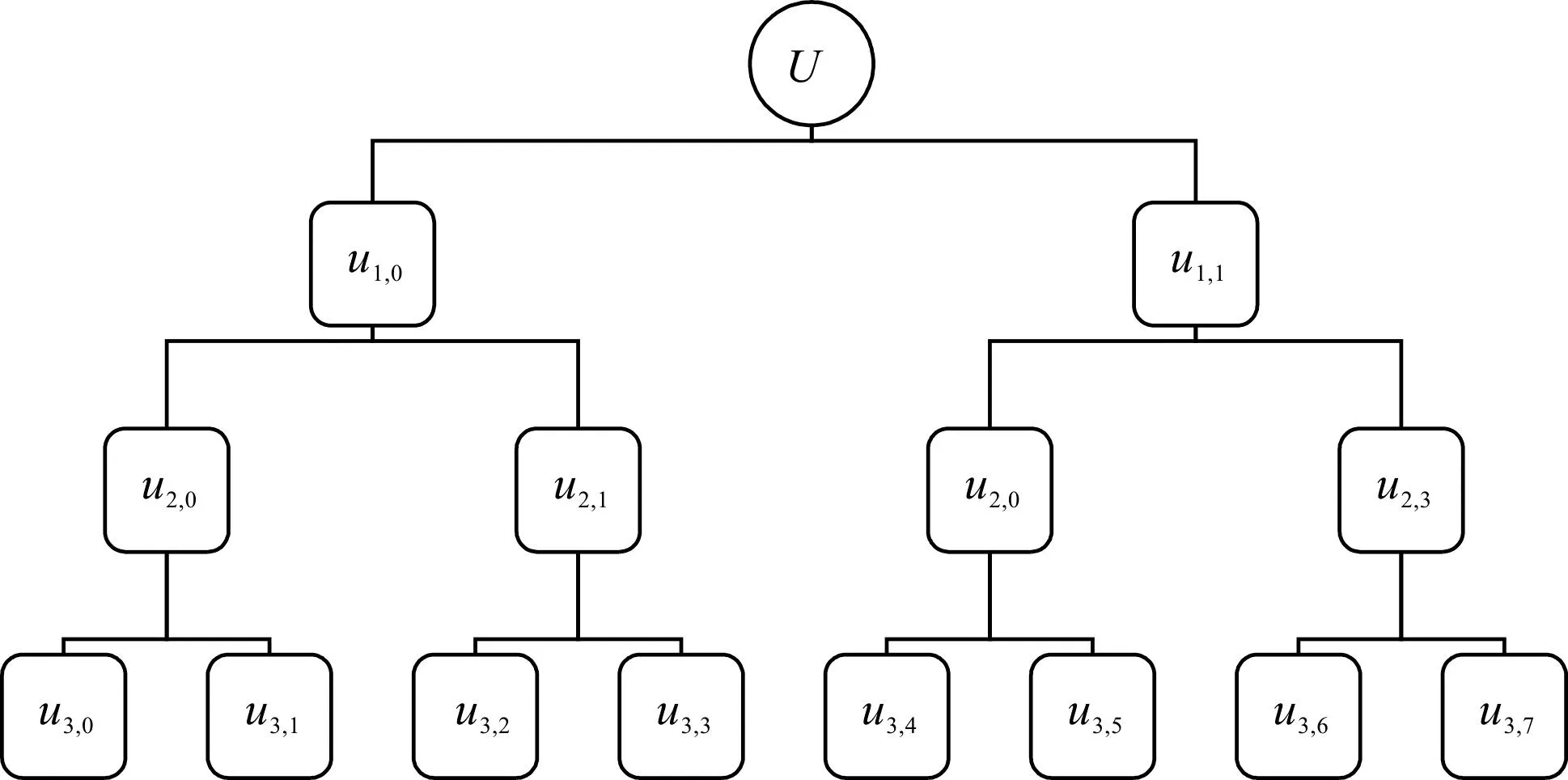
圖1 信號u(i)的層次分解示意圖(k=3)Fig.1 Schematic diagram of hierarchical decomposition of signal u(i)(k=3)

4)對每個層次分量進(jìn)行RFDE分析,得到2k個層次分量的RFDE值,完成了信號的HRFDE計算任務(wù)(過程),其表達(dá)式為:

HRFDE=RFDE(uk,e,m,c,d)

(8)

綜合上述分析,與MRFDE的粗粒化處理不同,HRFDE的層次分析將信號拆分為算子Q0和算子Q1,分別從低頻和高頻來表征信號的固有特性,使信號的復(fù)雜性分析更加全面和準(zhǔn)確。

對于實際工程中的旋轉(zhuǎn)機(jī)械而言,振動信號的高頻部分也包含大量的故障信息,只利用信號的低頻無法完全表征故障特性,充分利用信號中的高頻信息很有必要。

1.3 參數(shù)設(shè)置和仿真分析

根據(jù)HRFDE的計算過程可知,對結(jié)果存在影響的參數(shù)包括:信號長度N、嵌入維數(shù)m、類別數(shù)c和時間延遲d。現(xiàn)分述如下:

1)m的設(shè)置會影響信號重構(gòu)時重構(gòu)向量的信息量,m過小會導(dǎo)致重構(gòu)時丟失部分信息;反之m過大,會嚴(yán)重降低計算效率;

2)c的選擇會影響模式的歸類,c過小會導(dǎo)致幅值差距較大的散布模式被歸為一類;反之c過大,會導(dǎo)致算法的抗噪性較差;

3)時間延遲d對算法的性能幾乎沒有影響。

宋來建等人[13]126對參數(shù)進(jìn)行了研究。根據(jù)其建議,筆者將參數(shù)設(shè)置為m=2、c=5、d=1。

為了獲得合理的數(shù)據(jù)長度,筆者對不同長度下的白噪聲進(jìn)行了研究。

不同長度白噪聲信號的HRFDE結(jié)果,如圖2所示。

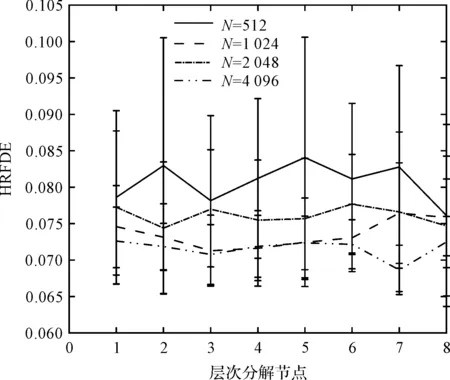
圖2 不同長度白噪聲信號的HRFDEFig.2 HRFDE of white noise signals of different lengths

由圖2可知:不同長度白噪聲信號的HRFDE曲線均存在波動,但隨著長度的增加,波動的趨勢逐漸減弱,表明數(shù)據(jù)長度的增加有助于提高熵值的穩(wěn)定性;此外,隨著數(shù)據(jù)長度的增加,信號標(biāo)準(zhǔn)差也逐漸減小,但計算效率也隨之降低。

因此,綜合考慮算法的性能和效率,筆者將長度設(shè)置為N=2 048。

隨后,為了對比HRFDE和MRFDE的性能,筆者構(gòu)造了20個長度為2 048的白噪聲信號,并分別利用HRFDE和MRFDE提取其反向波動散布熵值,同時計算了每個尺度的標(biāo)準(zhǔn)差,以評估算法的穩(wěn)定性。

白噪聲信號的HRFDE和MRFDE結(jié)果如圖3所示。

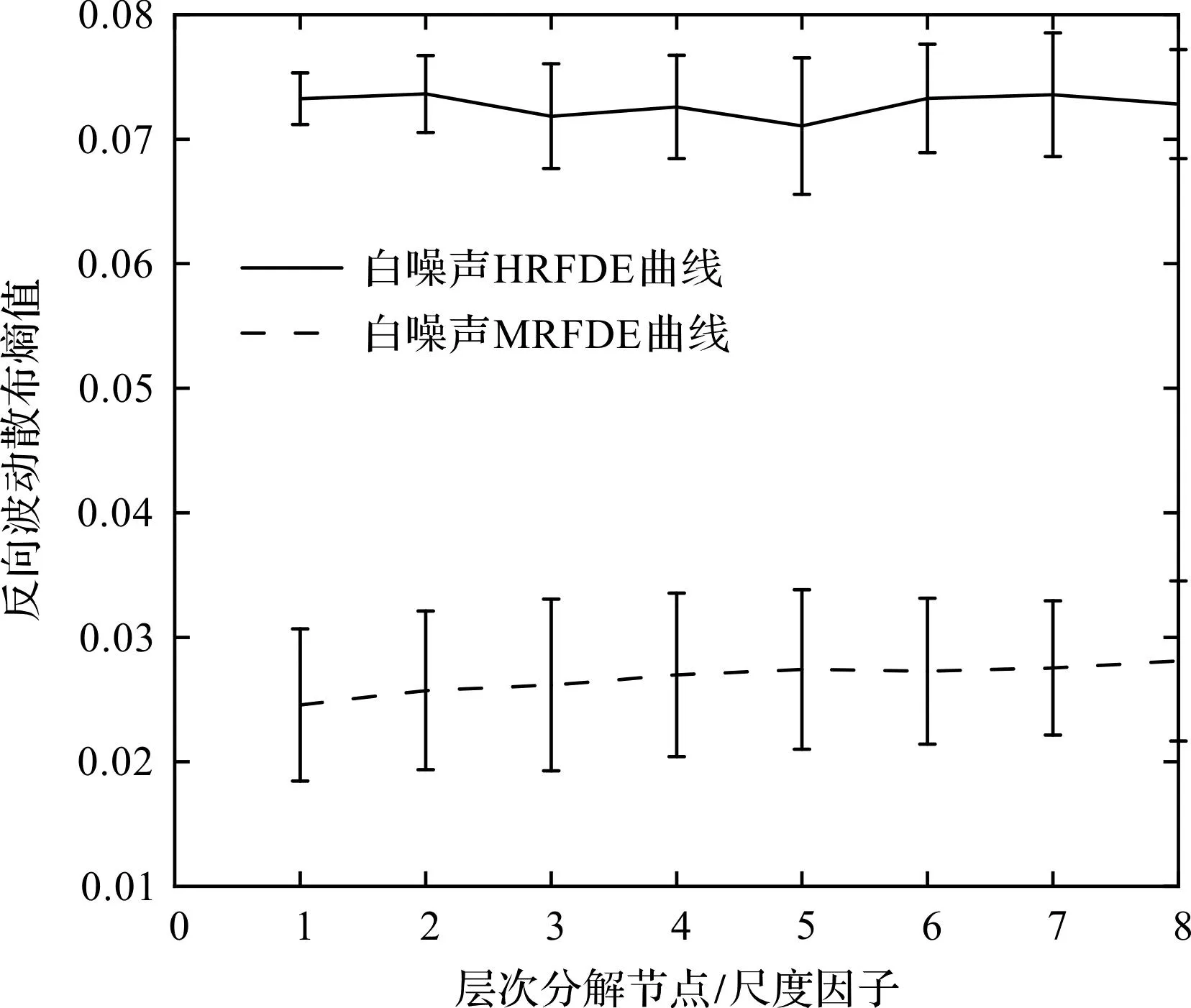
圖3 白噪聲信號的HRFDE和MRFDEFig.3 HRFDE and MRFDE of white noise signal

由圖3可知:對于白噪聲信號而言,通過HRFDE計算得到的熵值隨著層次節(jié)點而平穩(wěn)變化,熵值變化與節(jié)點的變化相互獨立,這與不同頻帶上白噪聲的熵值近似不變的結(jié)論一致。而MRFDE計算的白噪聲熵值會隨著尺度的增加而逐漸變大,這與白噪聲在各個頻帶具有一致復(fù)雜度的結(jié)論不符。這是由于MRFDE只提取了模擬信號的低頻信息,遺漏了對應(yīng)的高頻信息,而HRFDE能夠同時提取信號的低頻和高頻信息,從而獲得更多有效和全面的信息。

此外,觀察HRFDE和MRFDE的熵值誤差棒可以發(fā)現(xiàn),HRFDE曲線的誤差棒明顯小于MRFDE的誤差棒,證明HRFDE的穩(wěn)定性優(yōu)于MRFDE。

2 GSA-PNN分類器

2.1 概率神經(jīng)網(wǎng)絡(luò)

概率神經(jīng)網(wǎng)絡(luò)(PNN)是在徑向基神經(jīng)網(wǎng)絡(luò)的基礎(chǔ)上,結(jié)合了密度函數(shù)估計和貝葉斯決策理論而得到的一種神經(jīng)網(wǎng)絡(luò),其在樣本分類領(lǐng)域得到了廣泛的應(yīng)用。滾動軸承樣本為非線性和非平穩(wěn)的信號,可充分利用PNN在處理非線性樣本時具有高精度的優(yōu)勢[17]。

概率神經(jīng)網(wǎng)絡(luò)由輸入層、模式層、求和層和決策層組成,其網(wǎng)絡(luò)的結(jié)構(gòu)如圖4所示。

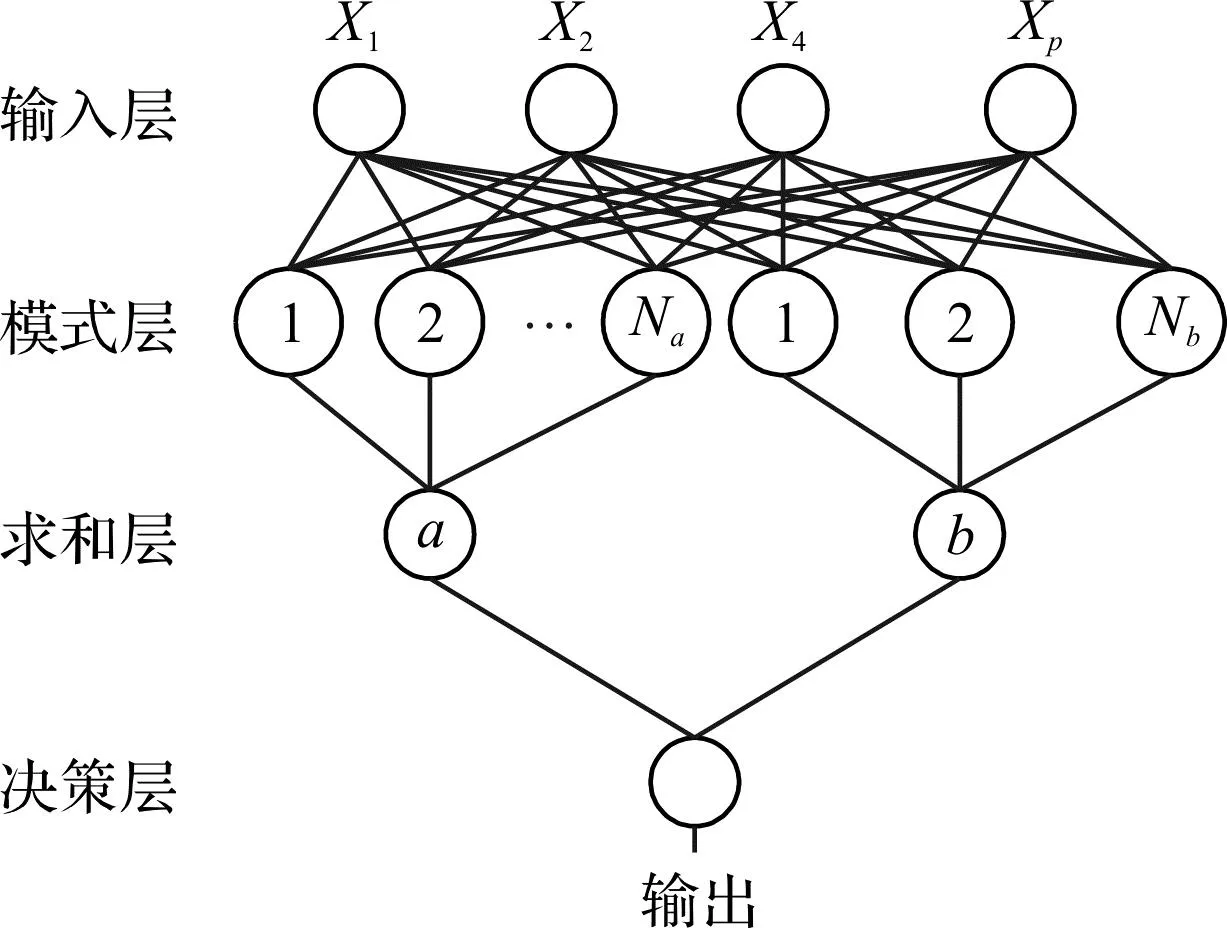
圖4 概率神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu)Fig.4 The structure of probabilistic neural networks

X為輸入樣本,X=(X1,X2,…,Xp);Na,Nb為輸入向量與中心的距離;a和b分別為不同的信息類型。

2.2 引力搜索算法

接下來,筆者采用引力搜索算法(GSA)對PNN進(jìn)行優(yōu)化。

GSA算法是ESMAT R等人[18]通過借鑒牛頓萬有引力的概念提出的一種新型的智能優(yōu)化算法,其利用種群中各物體之間萬有引力的相互作用,以此來實現(xiàn)優(yōu)化信息共享的目的。鄭近德等人[19]的研究已經(jīng)證明了GSA用于優(yōu)化的有效性。

GSA的具體原理如下:

假定有一個n維優(yōu)化空間,種群X={x1,x2,…,xn}其包含N個粒子,定義第i(i=1,2,…,N)個粒子的坐標(biāo)為:

(9)

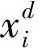
首先,對粒子的坐標(biāo)進(jìn)行初始化。在時刻t,第i個粒子和第j個粒子之間的引力值定義如下:

(10)

式中:Mpi(t)為受力粒子i的慣性質(zhì)量;Maj(t)為施力粒子j的慣性質(zhì)量;ε為無物理意義的常數(shù);G(t)為隨t變化的引力常量;Rij(t)為粒子i和j之間的歐式距離。

其次,適應(yīng)度值的大小關(guān)乎粒子的慣性質(zhì)量Mi(t),適應(yīng)度值越大,表示其越靠近最優(yōu)解。基于下式進(jìn)行粒子慣性質(zhì)量的更新:

(11)

(12)

式中:fiti(t)為粒子i在t時刻的適應(yīng)度值;best(t)為所有粒子中最好的適應(yīng)度值;worst(t)為所有粒子中最差的適應(yīng)度值。

在每一次的迭代中,粒子的速度和坐標(biāo)都會根據(jù)牛頓第二定律進(jìn)行更新,其公式如下:

(13)

(14)

(15)

實驗中,筆者設(shè)置GSA的種群數(shù)量為30,迭代次數(shù)為100,PNN的平滑因子初始值設(shè)置為0.1,優(yōu)化范圍設(shè)置為[0,1]。

GSA優(yōu)化PNN的詳細(xì)流程,即GSA-PNN優(yōu)化流程圖如圖5所示。

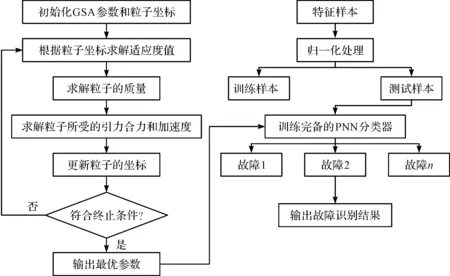
圖5 GSA-PNN優(yōu)化流程圖Fig.5 Optimization flow chart of GSA-PNN

3 基于HRFDE和GSA-PNN的診斷方法

鑒于HRFDE方法在進(jìn)行特征提取中的有效性和優(yōu)越性,筆者提出了一種基于HRFDE和GSA-PNN的旋轉(zhuǎn)機(jī)械故障診斷方法。

該診斷方法的具體流程如下:

1)采集n種不同工況的旋轉(zhuǎn)機(jī)械振動信號,將其分割為等長的h個樣本,對全部樣本進(jìn)行HRFDE計算,選擇前8個HRFDE值作為特征向量;

2)在不同工況樣本的特征向量中,隨機(jī)抽取i個樣本組成訓(xùn)練樣本,剩余樣本組成測試樣本;

3)利用訓(xùn)練樣本的特征向量對基于GSA-PNN的多故障分類器進(jìn)行訓(xùn)練,生成完備的訓(xùn)練模型;

4)將測試樣本輸入至訓(xùn)練完備的模型,根據(jù)模型的輸出來判斷旋轉(zhuǎn)機(jī)械的故障類型和嚴(yán)重程度。

4 故障診斷實驗與分析

4.1 軸承故障診斷實驗

4.1.1 故障數(shù)據(jù)來源

滾動軸承的實驗數(shù)據(jù)由美國凱斯西儲大學(xué)的軸承數(shù)據(jù)庫提供(該數(shù)據(jù)庫中的軸承型號為6205-2RS JEM SKF深溝球軸承)。

軸承實驗裝置如圖6所示。

圖6 軸承實驗平臺Fig.6 Bearing test platform

此處電機(jī)的負(fù)載設(shè)置為0 hp,轉(zhuǎn)速為1 797 r/min。基于不同的故障尺寸,筆者以12 kHz的頻率收集了驅(qū)動端滾動軸承在4種狀態(tài)下的10種工況的振動信號,其中故障尺寸分別為0.177 8 mm、0.355 6 mm、0.533 4 mm,故障的深度為0.279 4 mm。

對于每種工況均收集40組樣本,數(shù)據(jù)長度為2 048,同時為模擬實際條件下缺乏訓(xùn)練樣本的情況,筆者隨機(jī)抽取10組樣本用于訓(xùn)練,剩余30組用于測試。

樣本的詳細(xì)信息如表1所示。

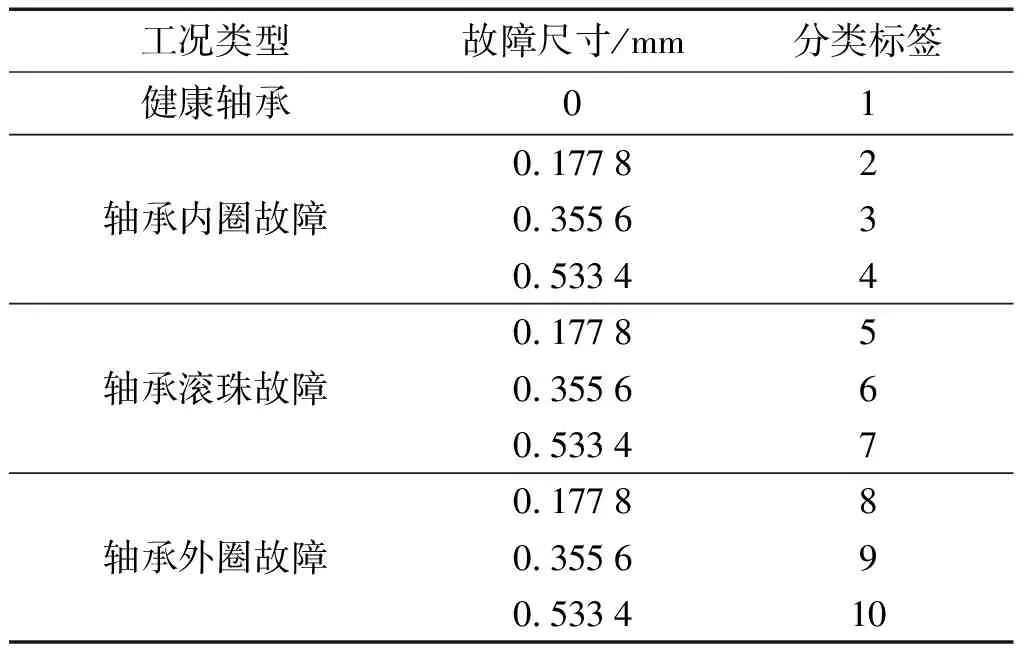
表1 滾動軸承實驗數(shù)據(jù)信息

滾動軸承振動信號的時域波形如圖7所示。

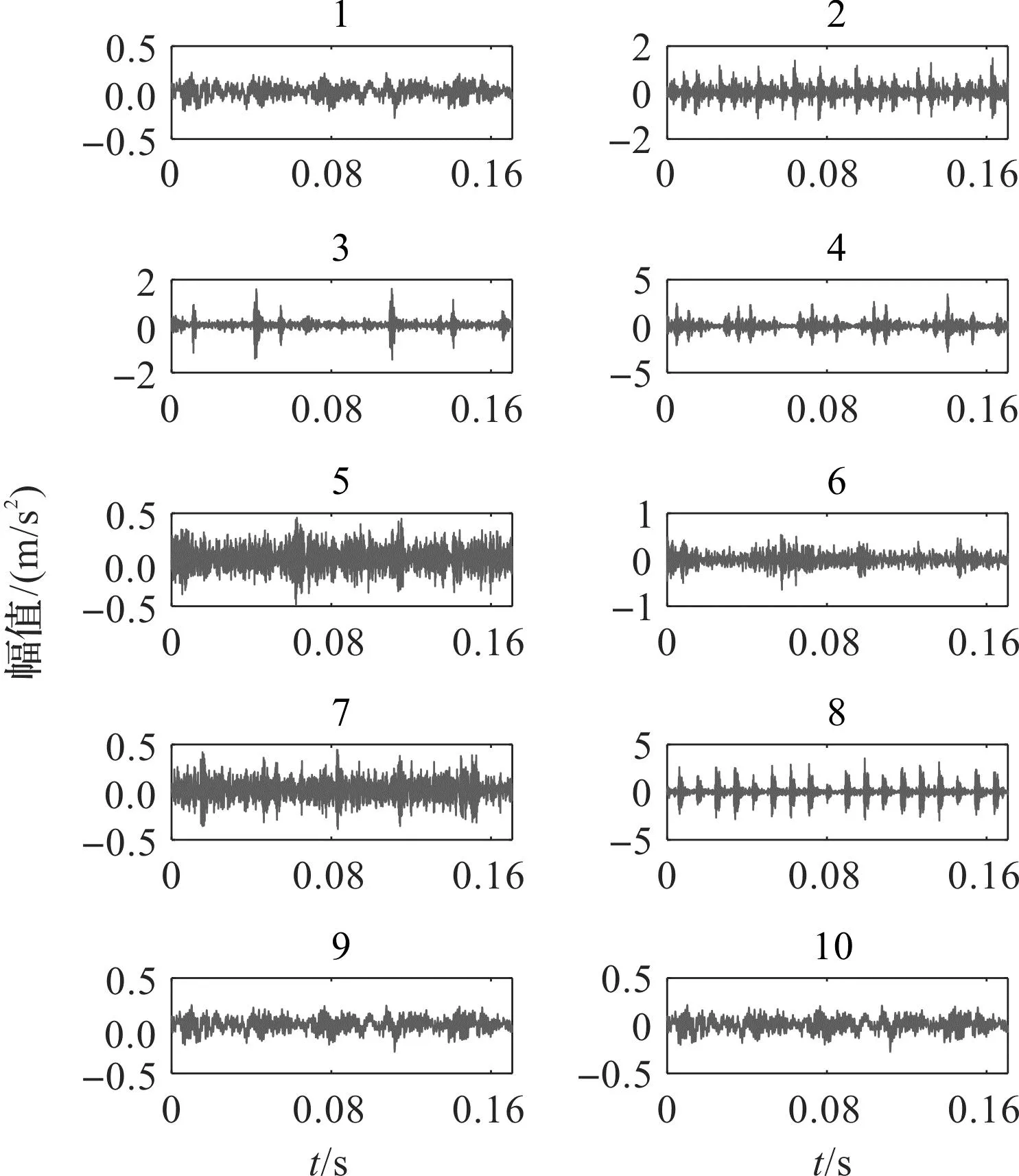
圖7 滾動軸承不同工況的振動信號Fig.7 Vibration signal of rolling bearing under different working conditions

筆者采用HRFDE提取滾動軸承樣本的故障特征,結(jié)果如圖8所示。

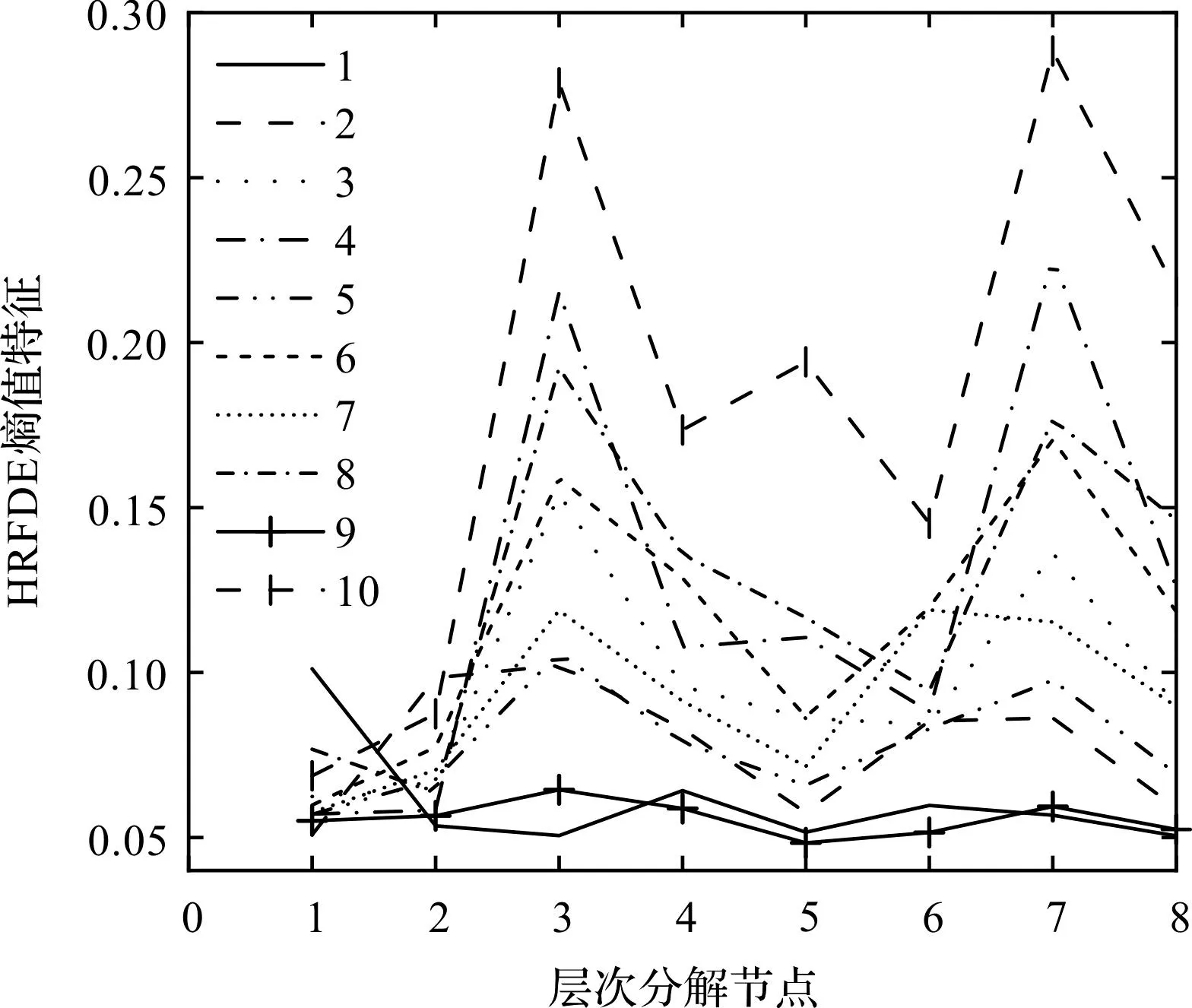
圖8 滾動軸承樣本的HRFDEFig.8 HRFDE of rolling bearing samples

由圖8可以看出:HRFDE具有良好的區(qū)分性能,不同節(jié)點上各個樣本具有較好的區(qū)分度,沒有出現(xiàn)明顯的混疊,證明HRFDE能夠從滾動軸承中提取出高質(zhì)量的故障特征。此外,還可以發(fā)現(xiàn)在尺度因子為1時,健康樣本的HRFDE值明顯大于其它故障樣本,且差異較大,這表明反向波動散布熵可以用于檢測軸承是否有故障,并設(shè)定閾值。

4.1.2 方法有效性驗證

為了進(jìn)一步識別滾動軸承的故障類型和嚴(yán)重程度,并判斷HRFDE方法的有效性,筆者將提取的HRFDE故障特征輸入至GSA-PNN分類器中,進(jìn)行訓(xùn)練和測試,得到了故障的識別結(jié)果和其混淆矩陣,如圖9所示。

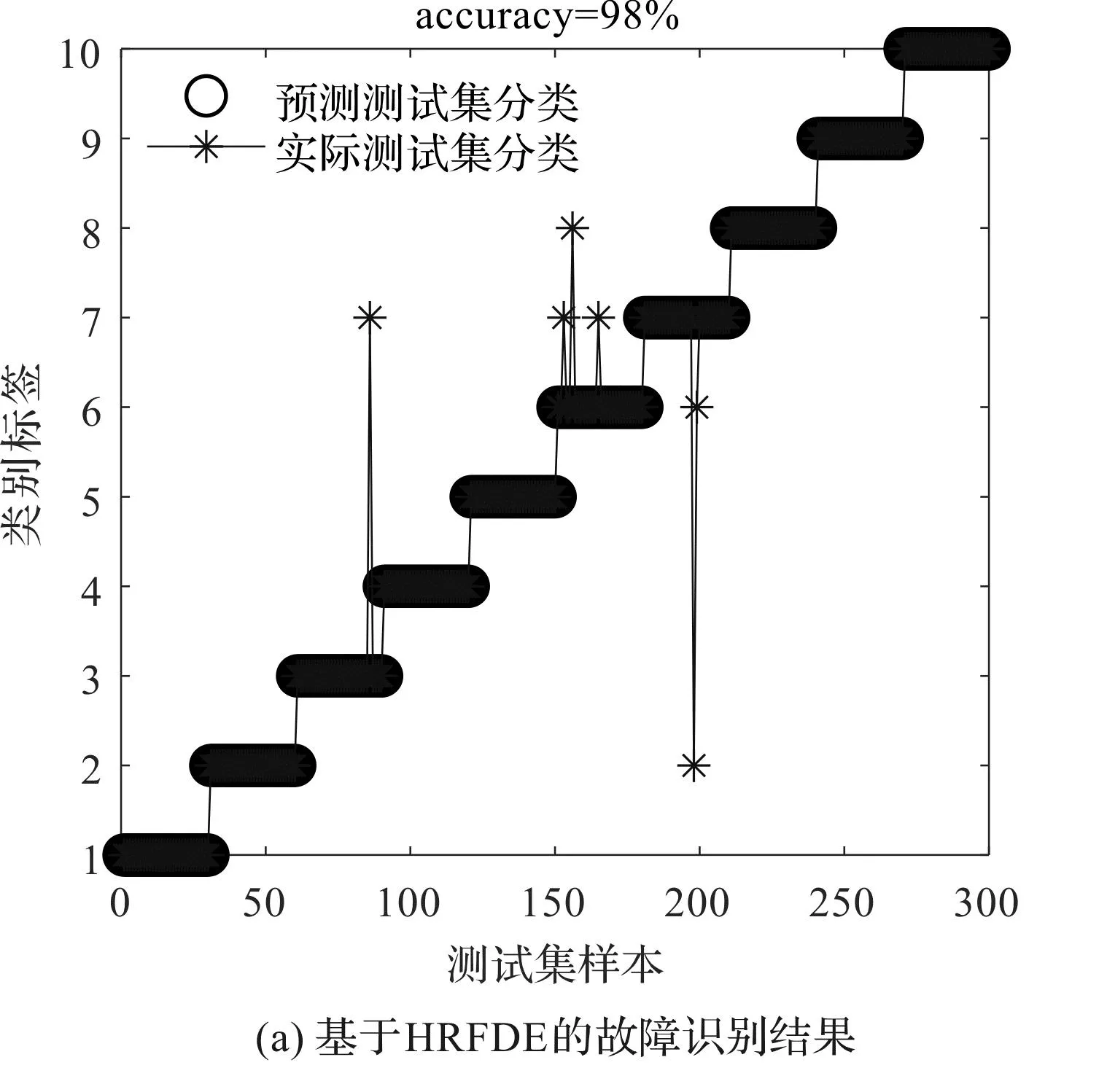
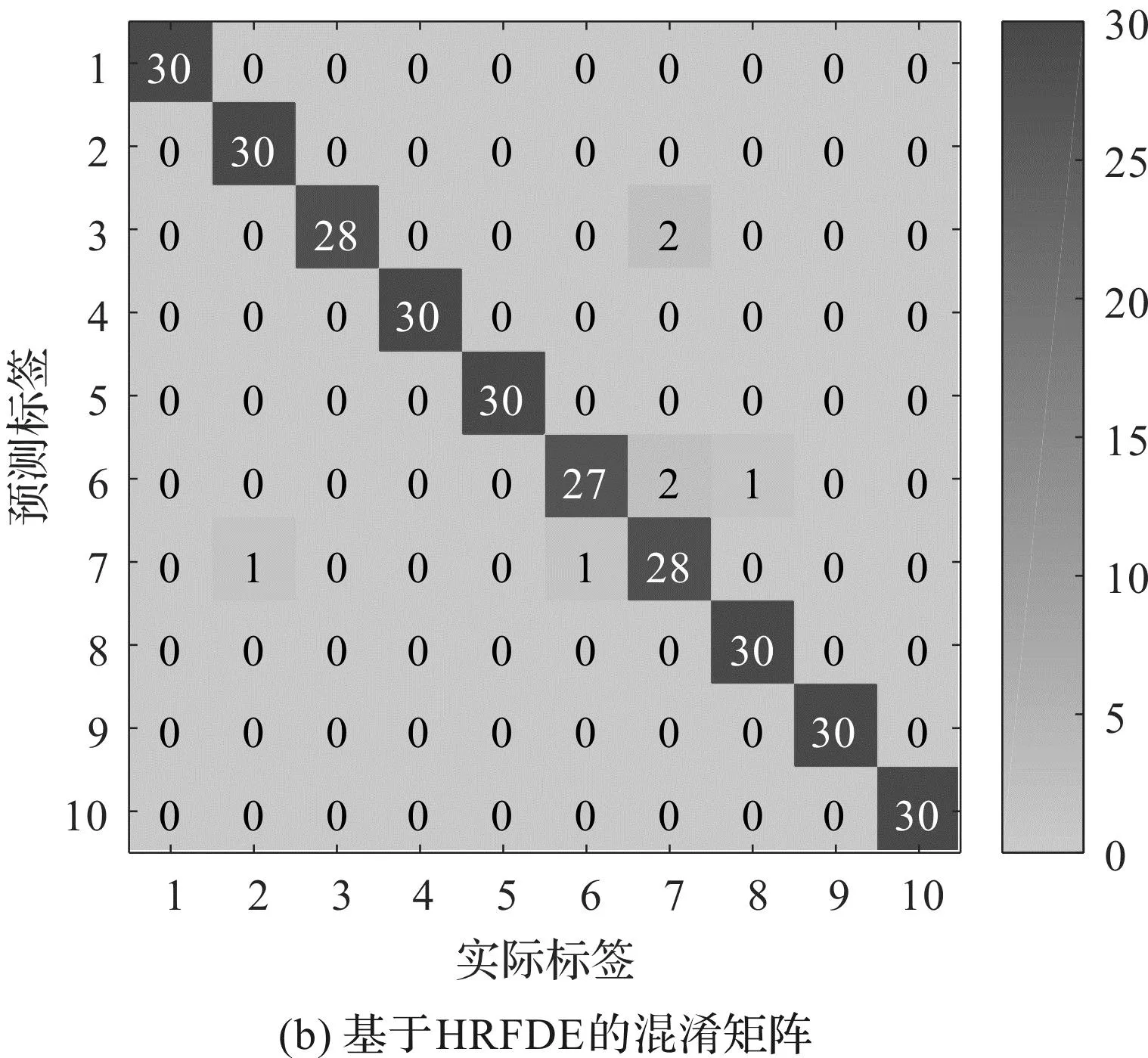
圖9 基于HRFDE和GSA-PNN的故障識別結(jié)果和混淆矩陣Fig.9 Fault identification results and confusion matrix based on HRFDE and GSA-PNN

從圖9可以發(fā)現(xiàn):采用基于HRFDE與GSA-PNN的故障診斷方法取得了98%的故障識別準(zhǔn)確率,有6個樣本被錯誤地識別為其他類型:

2個軸承內(nèi)圈故障(故障直徑0.355 6 mm)被錯誤識別為軸承滾珠故障(故障直徑0.533 4 mm);3個軸承滾珠故障(故障直徑0.355 6 mm)中有2個被錯誤識別為軸承滾珠故障(故障直徑0.533 4 mm),另外1個被錯誤識別為軸承外圈故障(故障直徑0.177 8 mm);有2個軸承滾珠故障(故障直徑0.533 4 mm)被分別錯誤識別為軸承滾珠故障(故障直徑0.355 6 mm)和軸承內(nèi)圈故障(故障直徑0.177 8 mm)。

總之,基于HRFDE和GSA-PNN故障診斷方法具有良好的性能,其能夠精準(zhǔn)地診斷滾動軸承不同故障類型和嚴(yán)重程度的故障。

4.2 齒輪箱故障診斷實驗

由于凱斯西儲大學(xué)軸承數(shù)據(jù)是在較為理想的狀態(tài)下采集得到的,因此,無法充分驗證基于HRFDE與GSA-PNN的故障診斷方法的通用性和有效性。

4.2.1 故障數(shù)據(jù)來源

為此,筆者采用江蘇千鵬故障診斷有限公司提供的齒輪箱故障實驗數(shù)據(jù),進(jìn)行算法的有效性和泛化性驗證。

齒輪箱故障模擬實驗平臺如圖10所示。

圖10 齒輪箱故障模擬實驗平臺Fig.10 Gear box fault simulation test platform

該平臺由原動機(jī)、軸承、齒輪箱、制動器和多個傳感器組成。筆者對傳感器4所采集的振動信號進(jìn)行分析。其中,齒輪箱中包含一個大齒輪和一個小齒輪,材料為S45C,通過油浸的方式進(jìn)行潤滑。

齒輪的參數(shù)如表2所示。

表2 齒輪的關(guān)鍵參數(shù)

齒輪箱數(shù)據(jù)集由5種工況下的振動信號組成,即健康齒輪、齒輪磨損、齒輪斷齒、齒輪點蝕和齒輪點磨(大齒輪點蝕、小齒輪磨損)。其中,齒輪點磨為復(fù)合故障,筆者替換齒輪箱中的齒輪來模擬不同的齒輪故障。

筆者將傳感器的采樣頻率設(shè)置為5.12 kHz,轉(zhuǎn)速設(shè)為880 r/min。5種工況的齒輪箱信號被均勻地分割為50組長度為2 048的樣本,共250組樣本。其中,每種工況隨機(jī)抽取30組數(shù)據(jù)作為訓(xùn)練集,剩余20組數(shù)據(jù)作為測試集。

實驗樣本的詳細(xì)信息如表3所示。

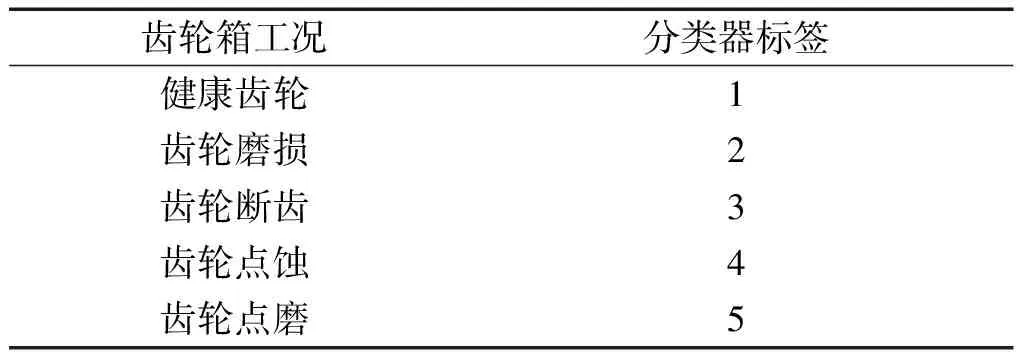
表3 齒輪箱樣本的詳細(xì)信息

齒輪箱振動信號的波形如圖11所示。

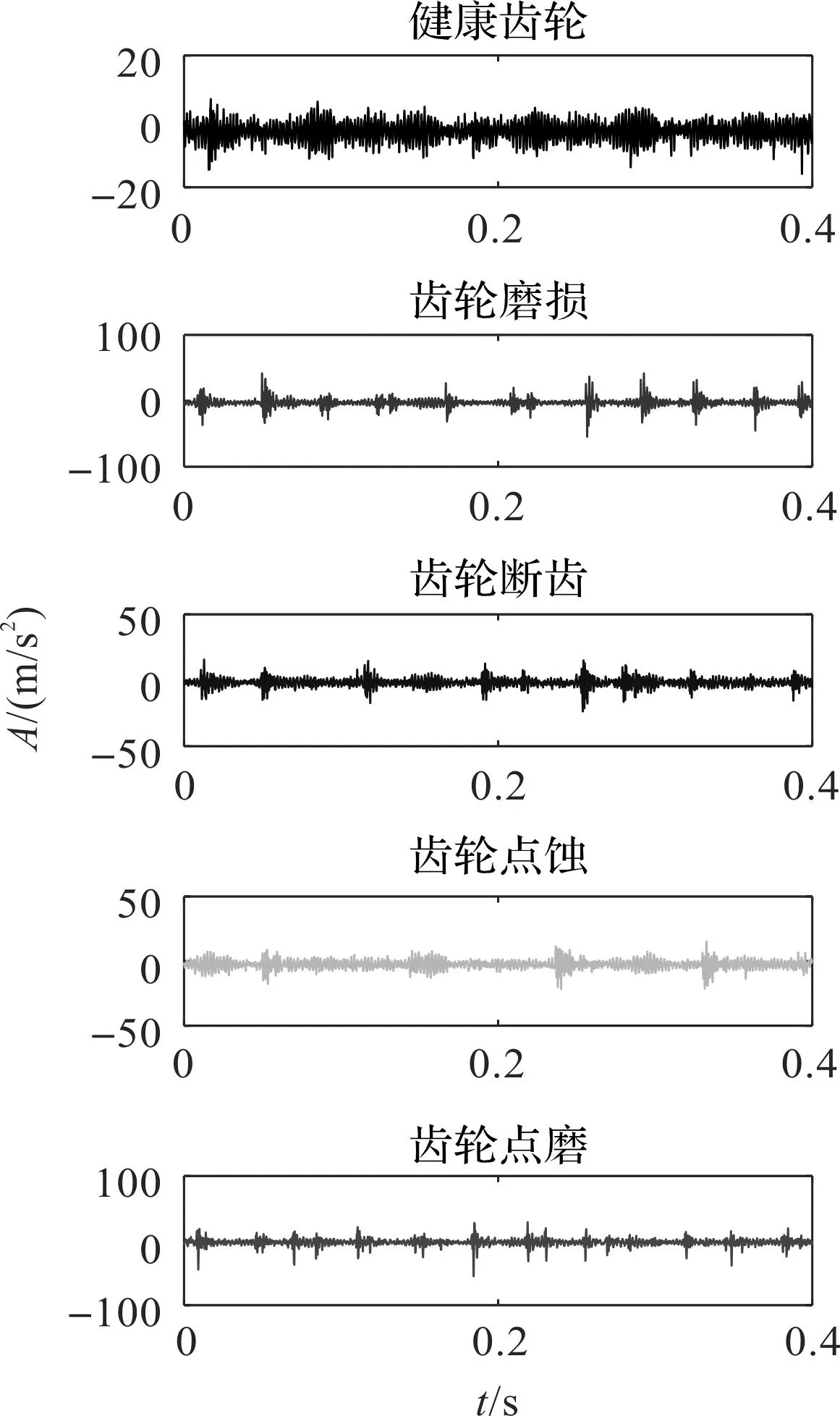
圖11 齒輪箱振動信號的波形Fig.11 Waveform of gear box vibration signal

首先,筆者對每個樣本進(jìn)行HRFDE分析,提取前8個節(jié)點的熵值作為故障特征。

4.2.2 方法優(yōu)越性驗證

為了驗證基于HRFDE與GSA-PNN的故障診斷方法的優(yōu)越性,筆者將該方法與MRFDE、MFDE、HDE進(jìn)行比較。4種方法的參數(shù)設(shè)置保持一致,即嵌入維數(shù)m=2,類別數(shù)c=5,時間延遲d=1。

采用不同方法得到的每種類型數(shù)據(jù)的均值如圖12所示。

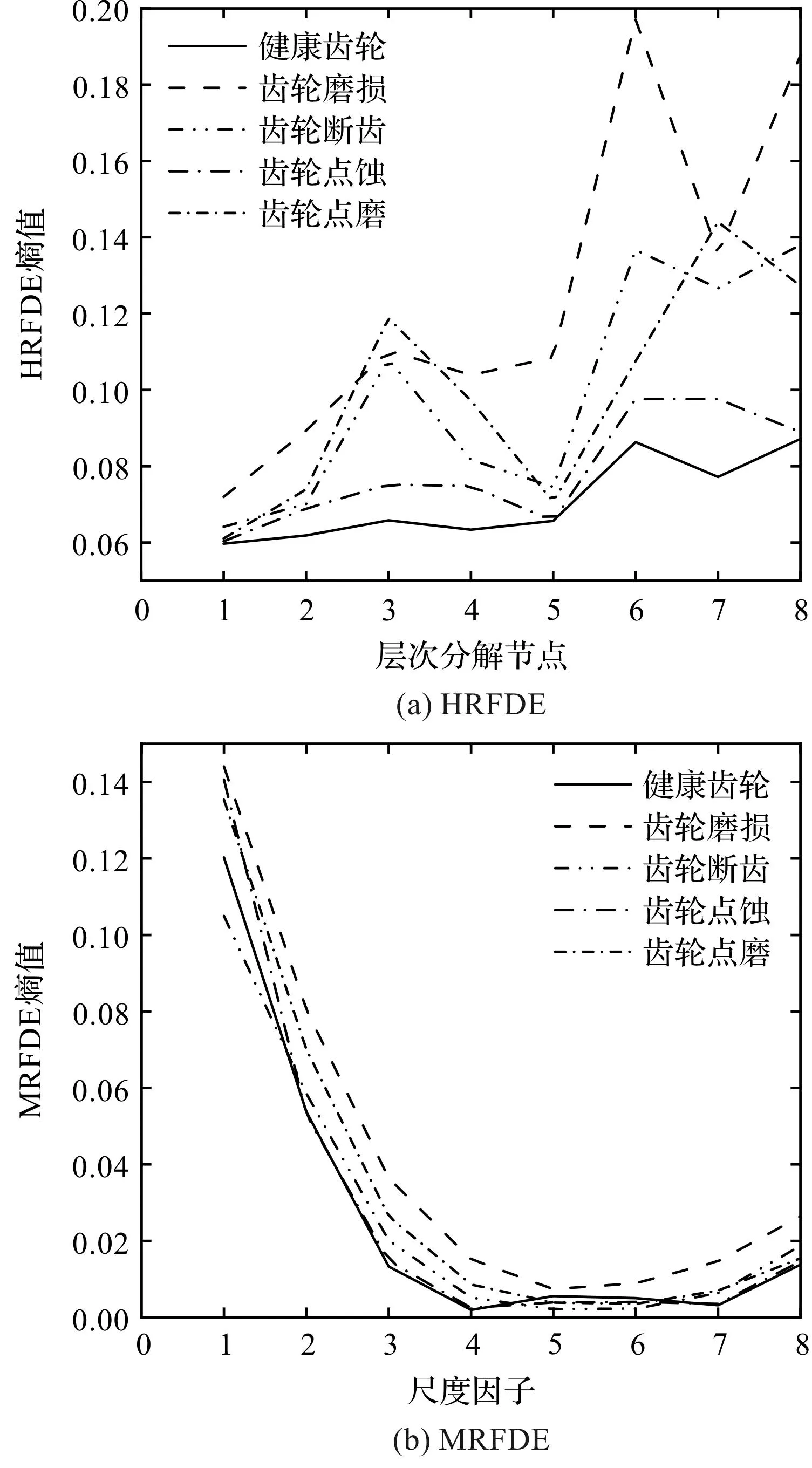
由圖12可知:HRFDE和HDE對樣本的區(qū)分度最佳,因為這2種方法能夠充分地提取信號中的高頻特征信息,因此特征質(zhì)量更好;而MRFDE和MFDE的熵值曲線出現(xiàn)了明顯的混疊,難以有效區(qū)分各個故障類型。

總之,在一定程度上,筆者可以根據(jù)熵值曲線判斷HRFDE方法優(yōu)于MRFDE和MFDE,但無法準(zhǔn)確評估和HDE的優(yōu)劣,需要結(jié)合GSA-PNN分類器進(jìn)行故障識別,以更準(zhǔn)確地評估HRFDE算法的有效性。

4.2.3 特征提取能力對比

為了評估4種方法的特征提取性能,并判斷故障的類型,筆者利用訓(xùn)練完備的GSA-PNN多故障分類器對測試樣本進(jìn)行識別,并得到了最終的診斷結(jié)果和混淆矩陣,如圖13所示。

從圖13可以發(fā)現(xiàn):基于HRFDE和GSA-PNN的故障診斷方法取得了98%的識別準(zhǔn)確率,較為準(zhǔn)確地診斷了齒輪箱的不同故障。

為了更加直觀地觀察4種方法的差異,筆者統(tǒng)計了不同方法進(jìn)行故障診斷時的診斷準(zhǔn)確率、錯誤識別數(shù)量和特征提取時間,得到采用不同方法的具體診斷

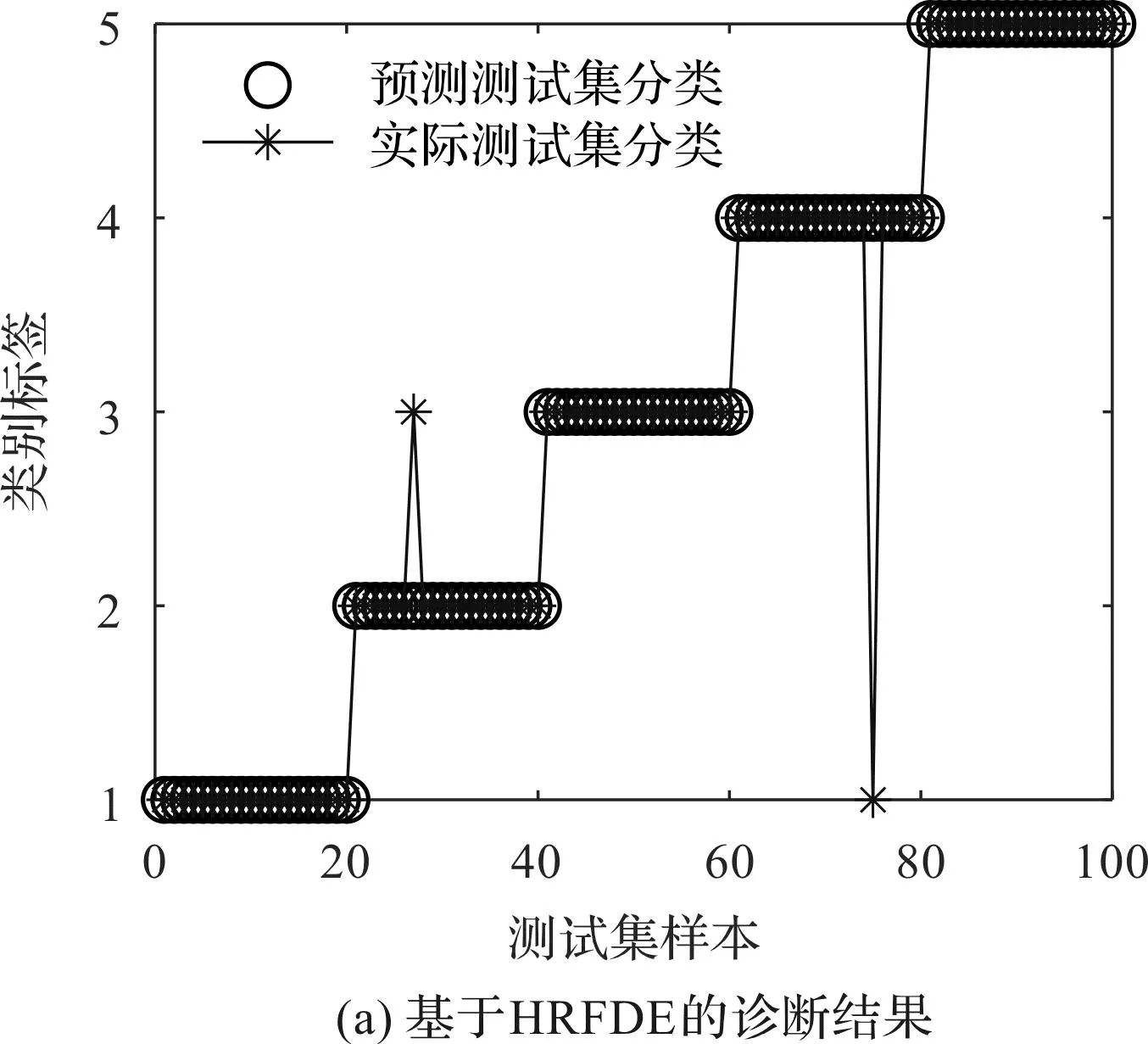
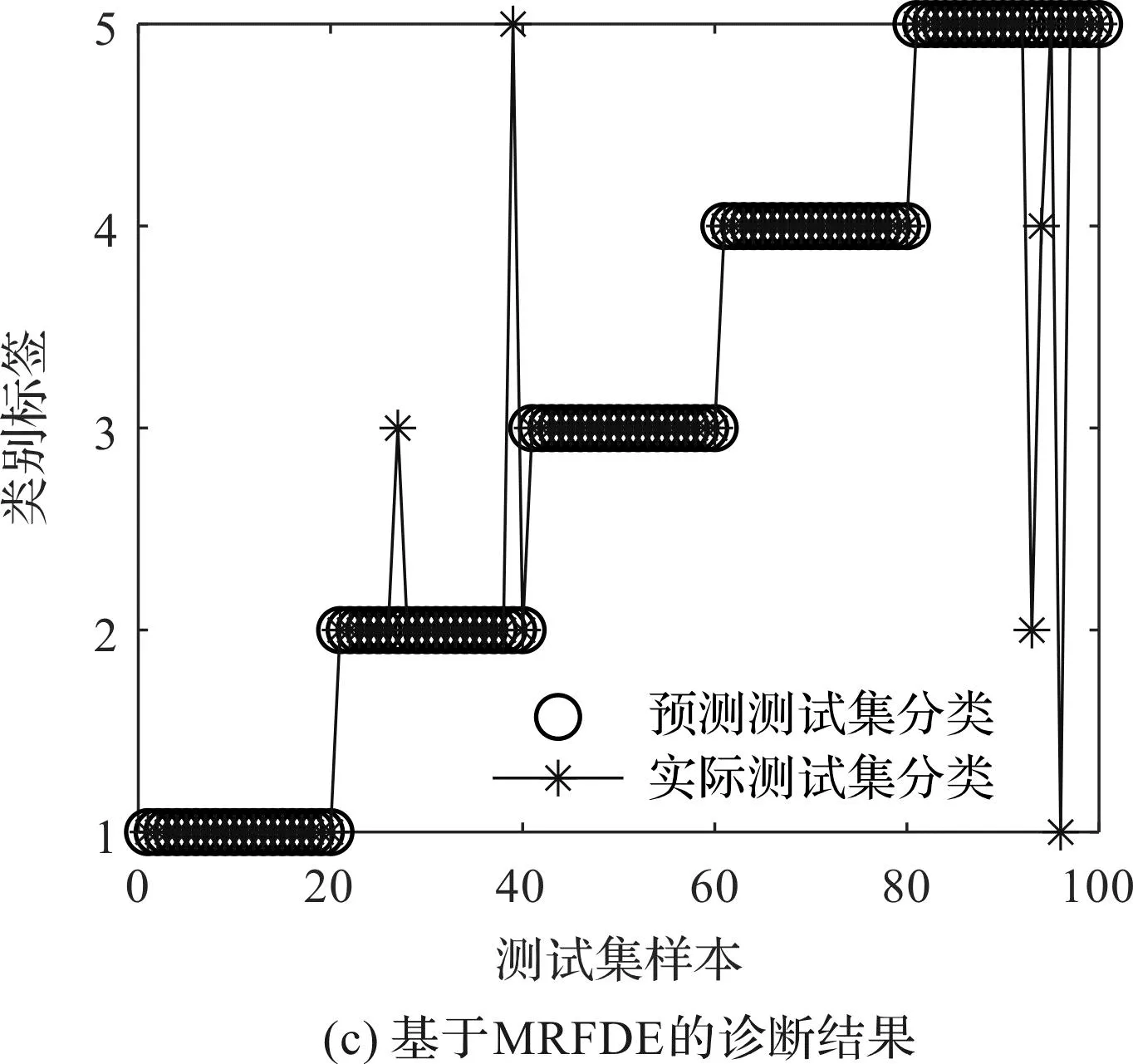
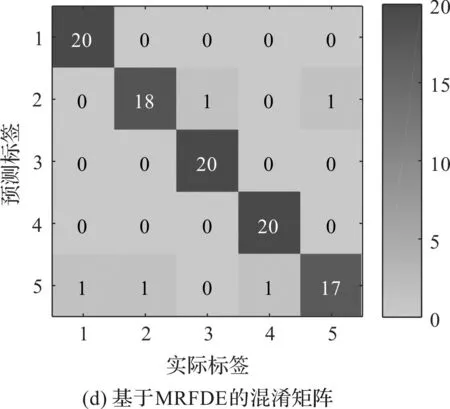
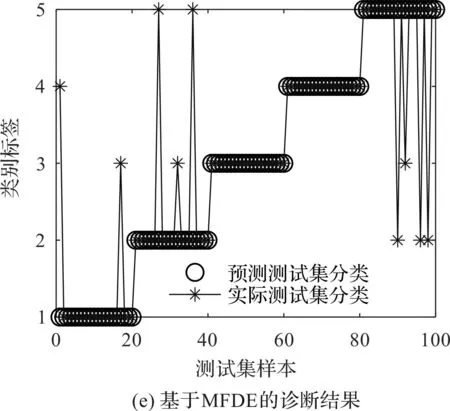
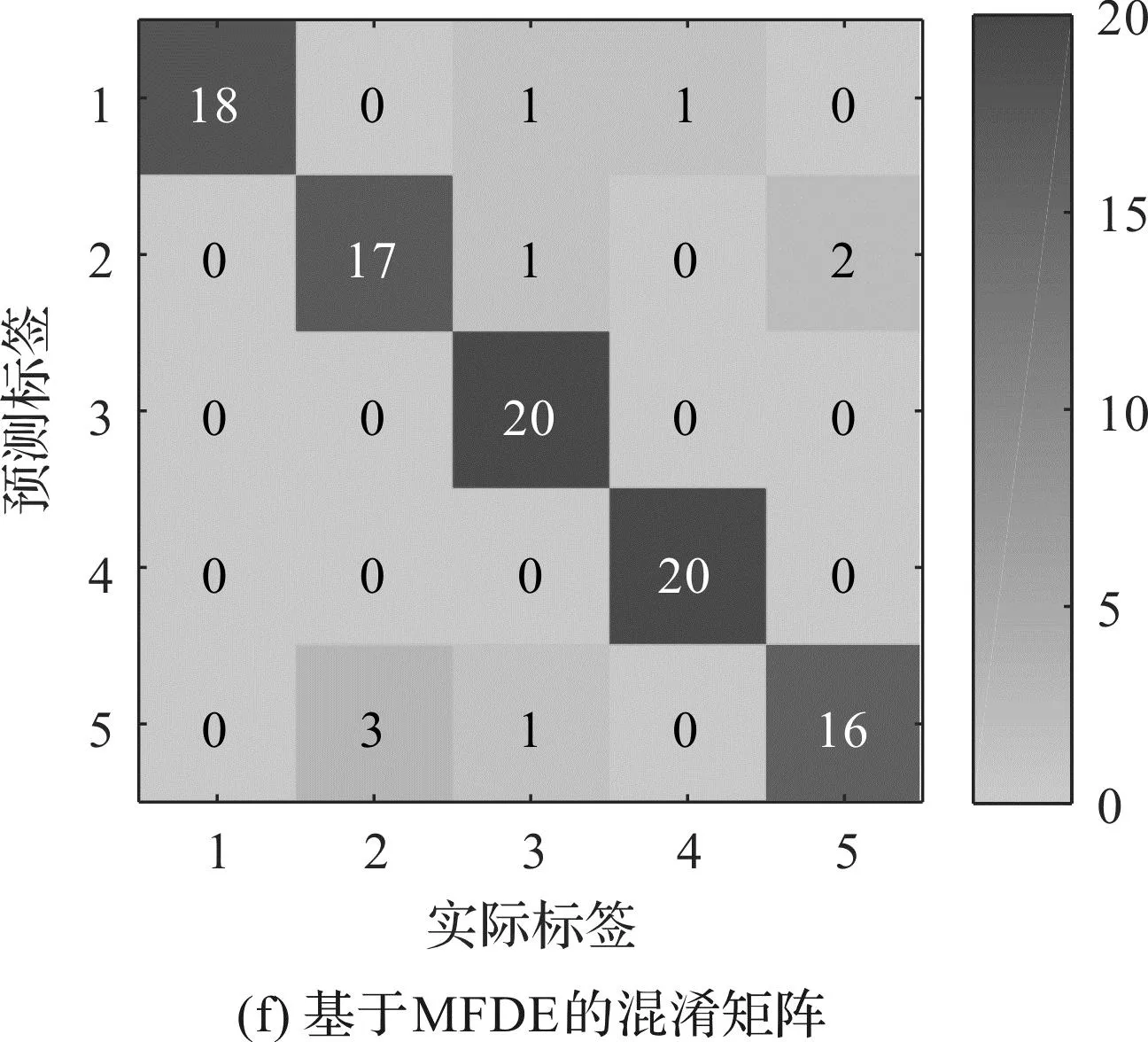
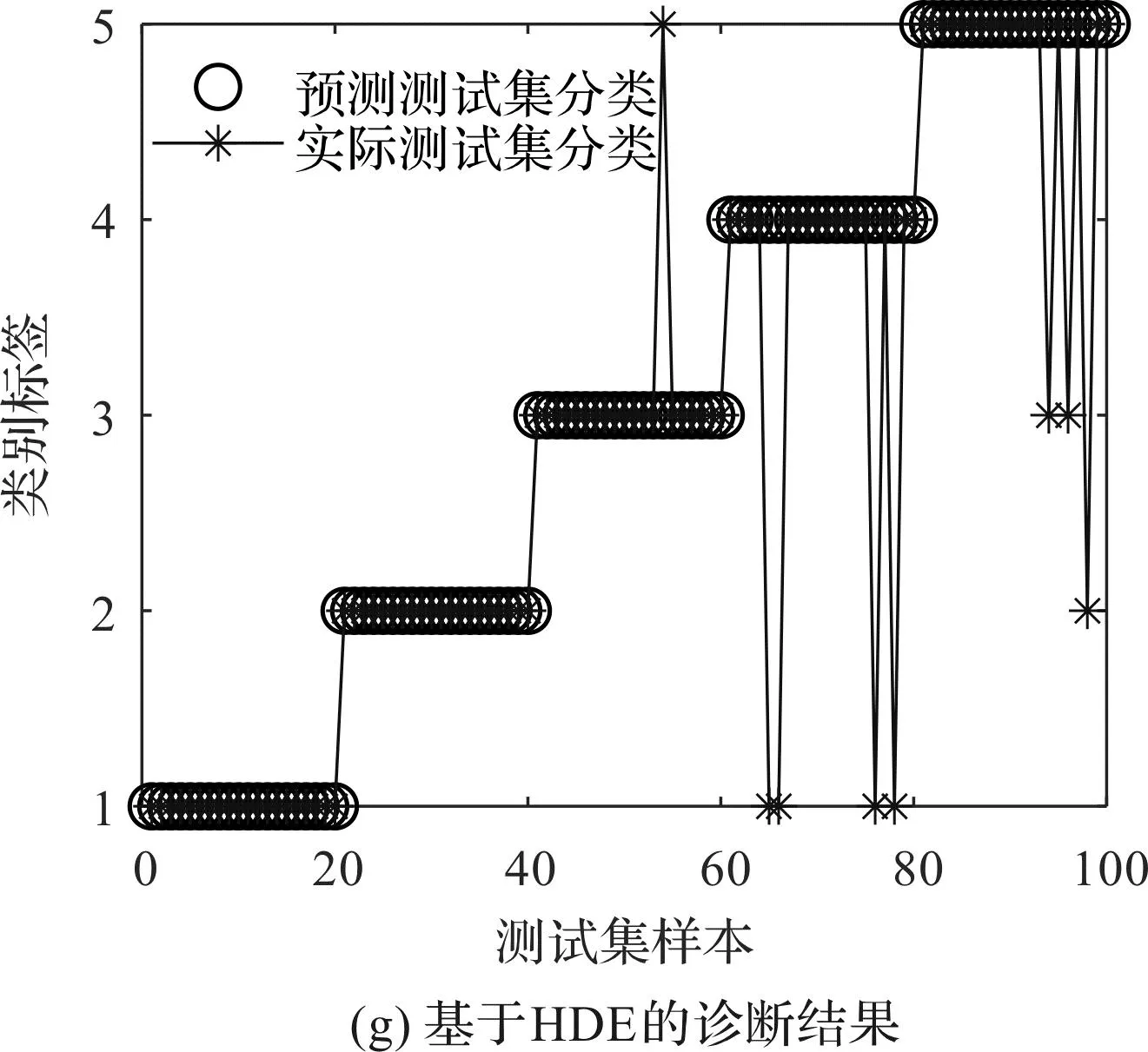
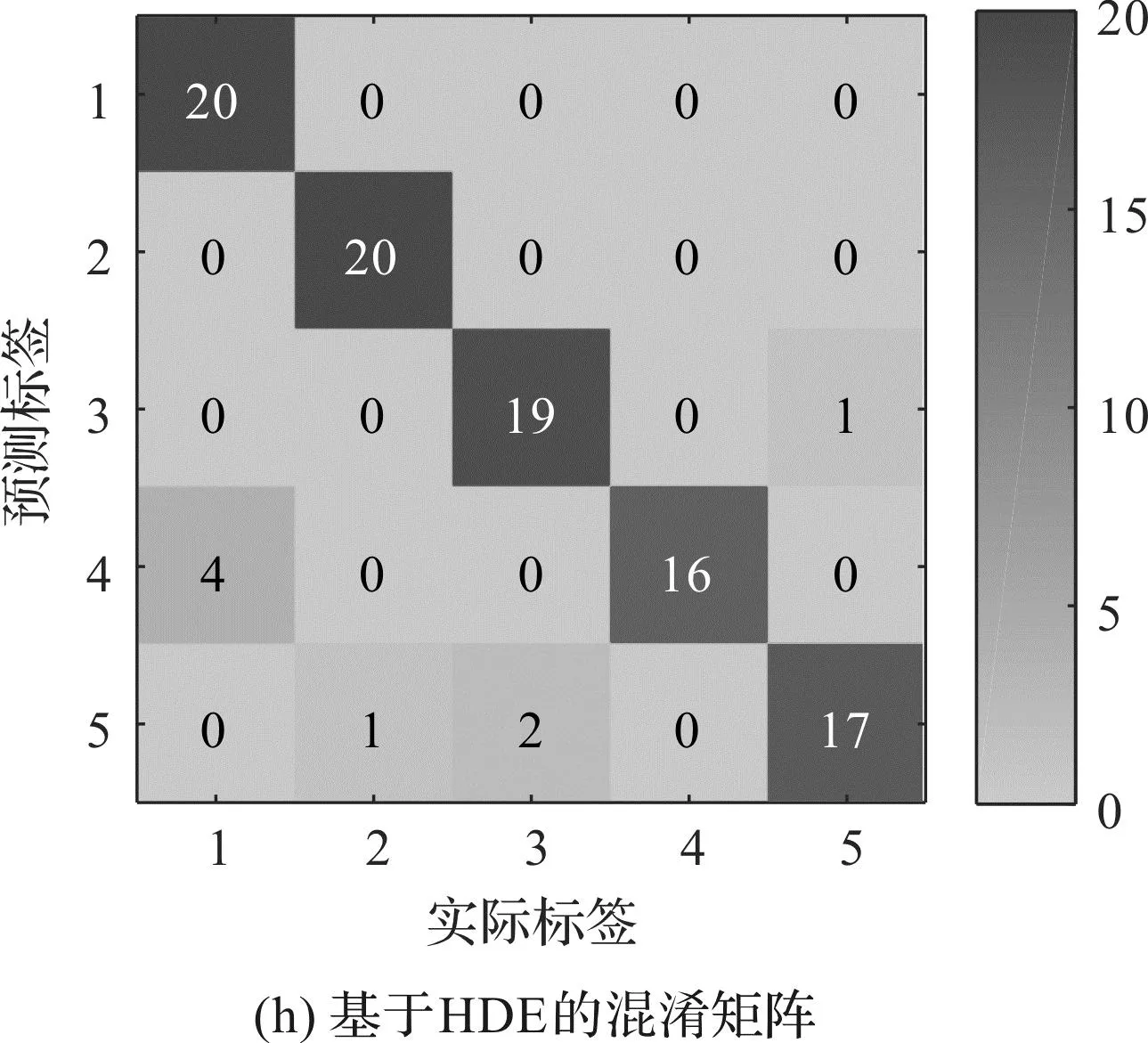
圖13 基于4種故障診斷方法的GSA-PNN診斷結(jié)果和混淆矩陣

結(jié)果,如表4所示。

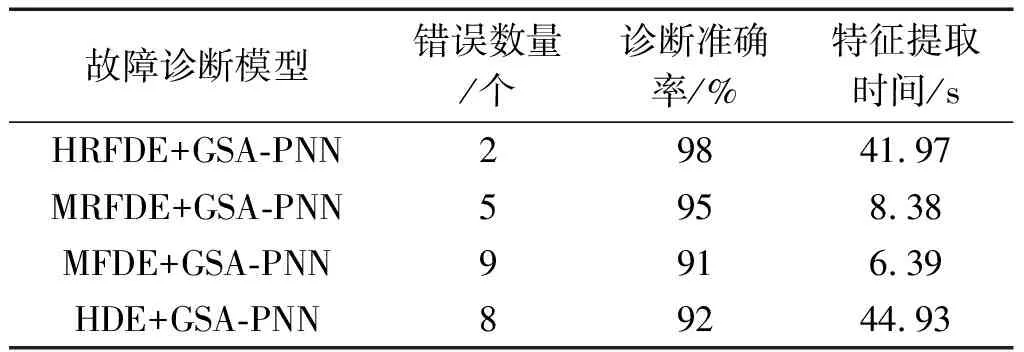
表4 不同方法的具體診斷結(jié)果

結(jié)合圖13和表4可知:HRFDE+GSA-PNN方法的準(zhǔn)確率最高,證明了該方法在特征提取中的優(yōu)越性;該方法的效率高于HDE+GSA-PNN,低于MRFDE+GSA-PNN和MFDE+GSA-PNN,但其僅需要41.97 s即可完成故障特征的提取,具有比較高的效率。

綜上可知,該方法具有比較優(yōu)異的性能。

由表4還可以發(fā)現(xiàn),上述4種方法的準(zhǔn)確率較為接近。

4.2.4 方法的穩(wěn)定性評估

為了進(jìn)一步對HRFDE+GSA-PNN方法的有效性(穩(wěn)定性)進(jìn)行評估,筆者重復(fù)進(jìn)行了5次實驗,得到了5次實驗下各方法的診斷結(jié)果,如圖14所示。

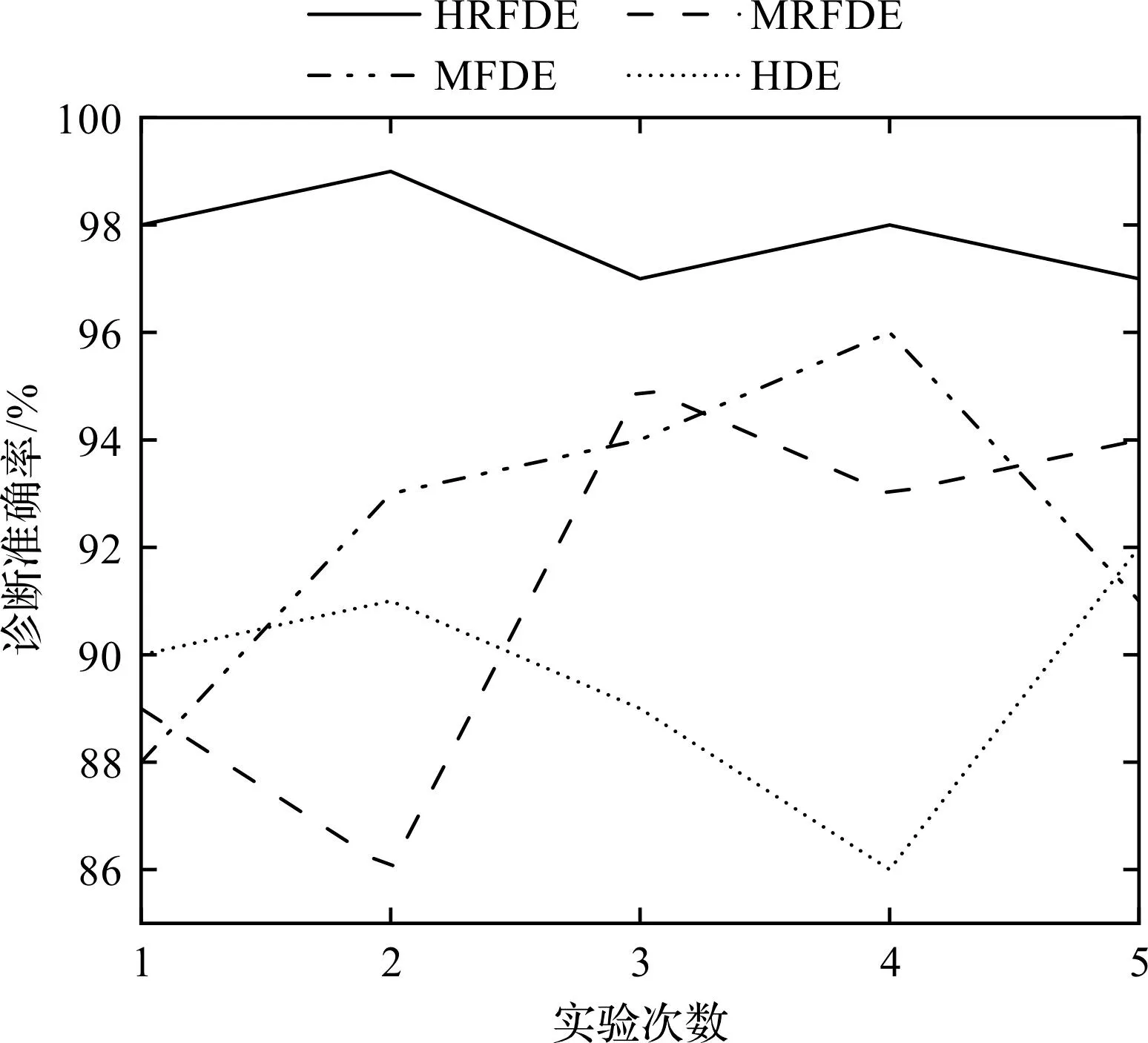
圖14 5次實驗下各方法的診斷結(jié)果Fig.14 The diagnostic results of each method under five experiments

由圖14可以發(fā)現(xiàn):經(jīng)過多次實驗,HRFDE+GSA-PNN方法的診斷準(zhǔn)確率均高于其他3種方法,證明了該方法具有極強(qiáng)的穩(wěn)定性。

同時,該方法的每次診斷準(zhǔn)確率均高于95%,說明其能夠準(zhǔn)確地診斷齒輪箱的故障。

5 結(jié)束語

針對旋轉(zhuǎn)機(jī)械的故障識別問題,筆者提出了一種基于HRFDE和GSA-PNN的旋轉(zhuǎn)機(jī)械故障診斷方法,并利用兩種旋轉(zhuǎn)機(jī)械數(shù)據(jù)集分別進(jìn)行了實驗,證明了該方法的有效性和優(yōu)越性。

研究結(jié)論如下:

1)HRFDE能夠較為準(zhǔn)確地刻畫時間序列中的高頻特征信息,白噪聲信號的HRFDE標(biāo)準(zhǔn)差均小于MRFDE的標(biāo)準(zhǔn)差,證明了HRFDE相對于MRFDE更穩(wěn)定;

2)將HRFDE用于旋轉(zhuǎn)機(jī)械故障數(shù)據(jù)分析,結(jié)果表明,HRFDE能夠從振動信號中提取較高質(zhì)量的特征,可靠地區(qū)分了旋轉(zhuǎn)機(jī)械的各個故障狀態(tài),識別準(zhǔn)確率均達(dá)到了98%;

3)建立了一種基于HRFDE和GSA-PNN的旋轉(zhuǎn)機(jī)械故障診斷方法,并基于兩種數(shù)據(jù)進(jìn)行了分析評估,結(jié)果表明:該方法的分類準(zhǔn)確率達(dá)到了98%,而特征提取時間為41.97 s,其綜合性能要優(yōu)于MRFDE、MFDE和HDE方法。

當(dāng)前,筆者在使用HRFDE方法進(jìn)行旋轉(zhuǎn)機(jī)械的故障識別時,沒有考慮其故障特征中的冗余,因此,后續(xù)筆者將結(jié)合特征選擇算法對HRFDE特征進(jìn)行優(yōu)化篩選。