整體意義理解下的結構化認知

荊熙哲

【摘 要】《義務教育數學課程標準（2022年版）》指出，要重視對教學內容的整體分析，強化對數學知識的本質理解，提煉出能打通數學知識之間的關聯、發揮核心作用的數學概念。本文對蘇教版數學四年級下冊“三角形、平行四邊形和梯形”單元重新編排，以“認識底和高”一課為例，從大單元的視角促進兒童對“高”這一數學概念的整體意義理解，使其形成結構化認知。

【關鍵詞】整體意義 概念教學 結構化認知

數學大單元教學的目的就是促進兒童對數學概念的整體意義理解。數學教學是對教材分段式實施的解讀與思考，是對單元內容整體性設計的探索與研究，是促進學生結構化認知的方式與策略，內容的結構化，知識的結構化，就是突破原有零散的知識點，形成結構化的知識網絡，建立相關聯的知識體系。“三角形、平行四邊形和梯形”單元是蘇教版數學四年級下冊中的內容，是小學階段“圖形與幾何”中十分重要的基礎知識之一。教材以“三角形的特征、底和高；三角形的三邊關系、內角和、分類；平行四邊形的特征、底和高；梯形的特征及底和高”的順序進行了編排。

從編排上不難發現，蘇教版的教材按照圖形的類型分別安排教學，雖然在教學平行四邊形和梯形時，會以三角形的學習經驗為依據進行探究，但在目前教學時間較為分散的情況下，學生很難理解知識點之間的聯系，難以深入理解本質，特別是幾何圖形中比較抽象的“底和高”。從學生的角度來看，如果把對認識三角形、平行四邊形和梯形整合在一節大課中進行探究，將認識底和高整合成一節課，就能更好地把握學習的重點。這樣的課堂具有較強的結構性，對幫助學生全面深入理解圖形的特征、“高”的本質具有很高的價值。

本文以“認識底和高”為例，從單元統整的角度思考，分析教材、重組教學、強化結構。在教學“認識底和高”一課前，學生前測的數據顯示，學生在二年級時對平行四邊形、梯形、三角形有了直觀的了解，認識它們的特征。但是在“高”的理解上，大多數學生把生活中的高和數學中的“高”混為一談，概念較為模糊，部分學生能在大腦中搜索到有關“垂線段”的知識來解釋，但是沒有人提到從哪里到哪里的垂直線段。

在教學環節的設計中，以梯形的高為起點，在貼近生活的同時，也更具有挑戰性，再把研究的方法和思路遷移到平行四邊形和三角形中，最后整體比較三角形、平行四邊形和梯形的高，聯想已有的知識經驗，把抽象的“高”和四年級上冊的“點到直線的距離”聯系在一起，通過比一比、聯一聯，深入理解“高”的本質。通過單元思維下的設計，“高”不再是模糊的，學生形成對“高”的整體性意義理解。通過這種學習方式，打破學生對原本模糊、抽象的“高”的認知，學生重新建立對“高”更全面、更深入的認識，使學科知識更具系統性、教學更具結構性，學生的學習可以更有效且富有挑戰性。下面截取本節課的部分教學片段，談幾點思考。

片段一：關聯生活，在原點到原型轉換中“識高”

在學生的數學學習中，對概念的理解都是借助于已有的生活，生活中的經驗是零星、熟悉的，也是可以隨機整合的。在這節課中，從學生生活中熟悉的橋洞出發，發現問題交流思考，既憑借經驗卻又超越已有經驗。

1.在生活的“高”中把握原點

師：走進生活的世界，我們先來看一段視頻。

教師播放視頻。

師：從視頻中你們看到了什么？大卡車為什么會撞上橋洞呢？

生1：小汽車經過了橋洞，但是大卡車撞上了。

生2：大卡車太高了，過不了橋洞。

生3：卡車的高已經超過橋洞的高了。

師（追問）：你們知道“限高”是什么意思嗎？

生1：橋洞的最大高度。

生2：能經過的汽車要比這個高度低。

生3：限制高度（字面意思）。

2.在對比的“高”中尋找原型

師：橋洞上面的“限高4.5m”指的是從哪里到哪里的距離？

學生指一指。

師（追問）：如果把橋洞看作一個梯形，想一想，“限高”是梯形中哪條線段的長度？

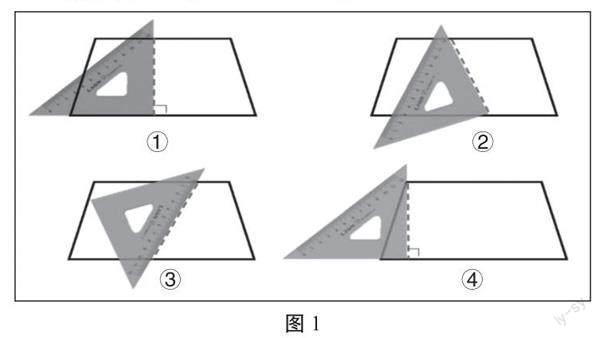
教師出示四種畫法（見圖1）。

師：哪條用三角尺畫出來的虛線可以表示剛才我們所說“限高”所在的線段？（①和④）它們有什么相同的地方？

生1：都是垂直的，是一條垂直線段。

生2：都在上底和下底之間。

生3：長度都是相等的。

師（追問）：你是怎樣想的？（兩條平行線之間的距離處處相等）

3.在表象的“高”中初步成型

師：其實，用三角尺這條直角邊畫出來的虛線就是梯形的高，而與另外一條直角邊重合的這條邊就是梯形的底，這就是今天要學習的梯形的底和高。你們發現了嗎？老師介紹了高后就介紹了底，所以底和高是對應出現的，而且我們剛才也說到，高應該是一條什么線段？

生：垂線段。

師：所以高是垂直于底的。

師：現在你們知道什么是梯形的高了嗎？

師：這時你還能找到梯形的高嗎？（將梯形順時針旋轉90°角）

學生指一指。

師：兩條腰之間有沒有高呢？

師：梯形的高也可以看作兩條平行線之間的垂直線段。

師：剛才我們認識了梯形的高，你們能畫一條梯形的高嗎？

學生交流畫“高”。

師：收集了一個學生的作品。

師：讓我們一起來看一看。

小結：畫高時要注意用虛線，標上直角符號，同時也要標出“高”和它對應的“底”。

【思考】學生對高的認識是建立在生活的場景中，通過卡車是否可以過橋洞這一情境，喚醒兒童的已有經驗，但是兒童對高的界定也是比較模糊的，尚未和已經學習的線段產生聯系。同時不同版本教材中對“高”的起始課大多是安排在三角形中，對比三角形，利用梯形作為起始導入，更易于學生理解，也更具挑戰性。用一段小轎車和大卡車過橋洞的對比視頻，引發學生的思考“為什么大卡車會撞上橋洞？”啟迪學生剝離生活情境的外衣，聯想生活中的“高”，從生活中對限高的理解，抽象出梯形的高，利用四幅圖讓學生選擇，在線段與線段的比較中打開學生對數學中“高”的初認識。學生有了一定的生活經驗，更容易建立“高”的模型，同時也為后續研究平行四邊形和三角形的高提供了思路和方法。

片段二：連續經驗，從單體到立體轉接中“建高”

學生對高的認識需要在梯形研究中遷移平行四邊形的高，從而對概念的理解從單向度的把握走向立體的承接。這個過程連續的是探索高的經驗。

1.遷一遷，在變形中遷移經驗

師：剛才我們通過生活中的限高認識了梯形的高，如果把梯形的上底延長，變成一個平行四邊形，你們能按照研究梯形的思路來研究平行四邊形的底和高嗎？老師給你們一個友情貼士。

2.做一做，在合作中積累經驗

教師出示學習單。

學習單

找一找：你能找出平行四邊形的高嗎？

畫一畫：用已有經驗畫出平行四邊形的高，并標出它的底。

想一想：你認為這樣的高有幾條？

比一比：平行四邊形的高與梯形比有什么相同和不同的地方嗎？

學生四人小組圍繞學習單展開研究，把自己的發現記錄在學習單上，最后在小組交流中形成小組意見。

3.說一說，在分享中再生經驗

教師實物投影展示小組的答案，并結合學生的回答，動態演示畫不同底上高的不同方法，展開三個層面的交流。

師：看看這兩個同學的“高的位置不同”的作品，你有什么發現？

生：雖然高的位置不同，但都是平行線之間的垂直線段，高有無數條。

師：看看這兩個同學關于“一種高”和“兩種高”的作品，你又有什么發現？

生：有兩種不同長度的高。

師：你知道這兩條高對應的底分別在哪里嗎？請指一指。

師：還有一個同學是這樣畫的，你有什么想說的？（呈現錯誤資源）

生：高應該是點到對邊所畫的垂直線段，在畫的時候可以用直角比畫一下。

小結：同學們不但畫出了高，還知道平行四邊形的高有無數條，平行四邊形有兩組平行線，所以能畫出兩種不同的高。

4.比一比，在比較中優化經驗

師：平行四邊形的高和梯形的高有什么相同和不同的地方呢？

生1：相同的是平行線之間垂直的線段就是梯形與平行四邊形的高，有無數條。

生2：不同的是梯形只有一組平行線，所以只有一個長度的高；而平行四邊形有兩組平行線，因此有兩個不同長度的高。

小結：看來梯形和平行四邊形的高都是兩條平行線之間垂直的線段，它們之間還有這樣的聯系呢！

【思考】活動經驗的積累讓學生對研究方法的遷移更得心應手。在研究了梯形的底和高后，學生不僅對高有了一定的理解，更對研究的方法、畫高的方法有了認知。在研究平行四邊形的高時，利用學生已有的點動成線的經驗，將平行四邊形與梯形緊密聯系在了一起，讓學生直觀地感受到，平行四邊形的高和梯形的高如出一轍，激發學生自主探究的動力和信心。在“大任務”的驅動下讓學生自主探究平行四邊形的底和高，并在交流中獲取知識。通過與梯形的對比，學生對“高”的認知不斷深化，其建構的知識網絡更加完整。在平行四邊形的探究中，學生再次感受到了學習方法和知識之間的聯系，進一步積累了活動經驗，為后續自主探究三角形的高起到了非常重要的鋪墊作用。

片段三：循環系統，在結構到建構轉化中“成高”

學生不僅借助已有的數學現實初步認識了“高”，而且在不同圖形的探究中積累經驗，在整體關聯中建立“高”的模型。學生站在整體化、系統化的高度展開結構化學習。

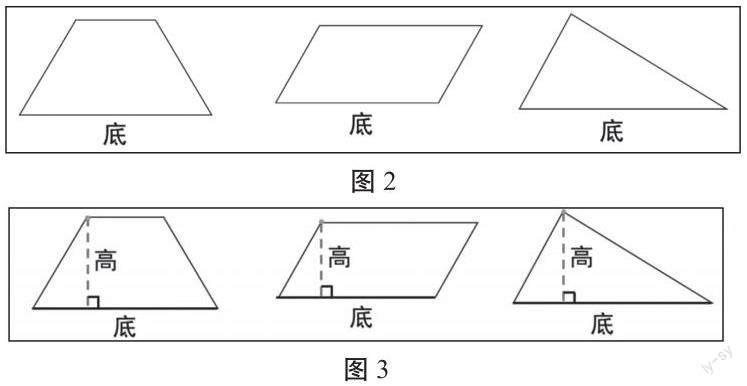
（1）找一找：請你找出底邊上的高（見圖2）。

比一比：請同學們仔細觀察三個圖形的高（如圖3），你們有什么發現？

小結：都過一點，都有底，都垂直于底。

（2）說一說：結合這三個發現，你們能不能說一說什么是高？

生1：高都是過一點作底的垂線段。

生2：這條垂線段就是高。

（3）聯一聯：聯結已有的知識模塊內化認知結構。

師：今天我們一起認識了底和高，你們能聯想到以前學過的類似知識嗎？

學生交流。

【思考】基于單元思維下展開的“高”的概念建立是整體、有意義的；從結構到建構，數學結構化學習是源自兒童整體的關聯的經驗，在自主探究出三角形的高后，利用一組簡單的練習，畫出底邊上的高，在鞏固知識的同時，激發學生進一步深入思考“高”的本質。通過圖形概念屬性探索達成對底和高的一致性，發展空間觀念與幾何直觀；通過“找一找”“比一比”“說一說”，發現“高”其實就是過一點所做的底的垂線段。最能起到畫龍點睛的是“聯一聯”，引導學生在聯系已有知識的同時，通過動畫，將三個圖形隱去，使學生直觀感受到高和原來學習的畫垂線是相同的。這一環節整體架構了“高”的知識網絡，讓學生在比較中建立“高”的模型，并且與已有知識建立關聯，體現了新課標理念提倡的一致性。