同構(gòu)函數(shù),妙解三角
程全平
? 江蘇省揚(yáng)州市仙城中學(xué)
三角函數(shù)是高中數(shù)學(xué)的基本知識內(nèi)容之一,也是高考考查的主干知識之一.三角函數(shù)作為一種特殊的函數(shù),在解決一些相關(guān)的三角函數(shù)問題時,經(jīng)常可以借助同構(gòu)函數(shù),回歸函數(shù)本質(zhì),挖掘函數(shù)內(nèi)涵,利用函數(shù)的相關(guān)概念、基本性質(zhì)、圖象等來巧妙轉(zhuǎn)化并加以處理.特別在解決三角函數(shù)中的參數(shù)取值、求函數(shù)值、大小比較、不等式證明等方面都有奇效[1].
1 參數(shù)取值
三角函數(shù)中的一些參數(shù)取值問題,經(jīng)常借助同構(gòu)函數(shù)思維,結(jié)合函數(shù)的基本性質(zhì)來恒等變形與轉(zhuǎn)化,為參數(shù)取值的求解提供條件[2].
例1(2022年廣東省汕頭市普通高考第二次模擬考試數(shù)學(xué)試卷·16)若cos5θ-sin5θ<7(sin3θ-cos3θ)(θ∈[0,2π)),則θ的取值范圍是______.
分析:根據(jù)題設(shè)條件,抓住三角關(guān)系式的共性特征進(jìn)行恒等變形與巧妙轉(zhuǎn)化.利用三角函數(shù)同名歸類,借助不等式的恒等變形,尋找不等式兩邊的共性,巧妙同構(gòu)函數(shù),進(jìn)一步利用導(dǎo)數(shù),合理確定函數(shù)的單調(diào)性,進(jìn)而利用函數(shù)單調(diào)性來轉(zhuǎn)化不等式,即可確定θ的取值范圍.
解析:由cos5θ-sin5θ<7(sin3θ-cos3θ),移項整理,可得cos5θ+7cos3θ 同構(gòu)函數(shù)f(x)=x5+7x3,x∈[-1,1],那么不等式cos5θ+7cos3θ 求導(dǎo)可得f′(x)=5x4+21x2≥0,則知函數(shù)f(x)在區(qū)間[-1,1]上是增函數(shù). 由f(cosθ) 點(diǎn)評:同構(gòu)函數(shù)來處理,相比三角恒等變形與轉(zhuǎn)化來說,更加簡單快捷,處理起來也更加巧妙.當(dāng)然,對于同構(gòu)函數(shù)單調(diào)性的判斷,也可以采用其他方式,如以上問題中先判斷冪函數(shù)y=x3和y=x5在相應(yīng)區(qū)間上的單調(diào)性,再綜合函數(shù)的運(yùn)算形式與對應(yīng)的單調(diào)性性質(zhì)來確定函數(shù)f(x)的單調(diào)性.而由三角不等式確定角的取值范圍時,也可以利用輔助角公式,結(jié)合三角不等式,借助三角函數(shù)的圖象與性質(zhì)來轉(zhuǎn)化. 三角函數(shù)的求值問題中,有時比較復(fù)雜難以直接下手,可以觀察三角關(guān)系式的結(jié)構(gòu)特征,合理恒等變形,巧妙同構(gòu)函數(shù),利用函數(shù)的基本性質(zhì)來變形與應(yīng)用,實(shí)現(xiàn)求函數(shù)值的目的. 分析:根據(jù)題中三角函數(shù)的特殊值,有意識地確定兩個特殊角滿足三角函數(shù)關(guān)系式,同構(gòu)三角函數(shù),確定其周期,結(jié)合求導(dǎo)處理以及三角函數(shù)關(guān)系式的恒等變形(和差化積公式),利用三角函數(shù)在一個周期長度內(nèi)的單調(diào)性來確定對應(yīng)角的取值,從而得以求解對應(yīng)的三角函數(shù)值. 故選擇答案:AC. 點(diǎn)評:此題以三角等式為問題背景,結(jié)合條件來求解相應(yīng)的三角函數(shù)值.常用的解題方法就是利用三角函數(shù)的公式變形來處理,過程比較繁雜,運(yùn)算量比較大.而抓住特殊角滿足的三角等式加以切入,巧妙同構(gòu)三角函數(shù),借助導(dǎo)數(shù)法來處理,思維性較強(qiáng),可以減少數(shù)學(xué)運(yùn)算,優(yōu)化解題過程[3]. 三角函數(shù)中也存在一些比較變量大小關(guān)系的問題,經(jīng)常可以借助題設(shè)條件,尋找特征,同構(gòu)函數(shù),進(jìn)而利用函數(shù)的基本性質(zhì)來合理轉(zhuǎn)化與巧妙應(yīng)用,實(shí)現(xiàn)大小關(guān)系的判斷. 例3已知實(shí)數(shù)a,b滿足asina-4bsinbcosb=4b2-a2+1,則以下各選項中大小關(guān)系正確的是( ). A.a>2bB.a<2b C.|a|>|2b| D.|a|<|2b| 分析:根據(jù)題設(shè)條件,結(jié)合題設(shè)中的等式進(jìn)行同一參數(shù)的變形轉(zhuǎn)化,實(shí)現(xiàn)等式兩邊的同型轉(zhuǎn)化,巧妙同構(gòu)函數(shù);結(jié)合函數(shù)的奇偶性,以及借助導(dǎo)數(shù)法判斷函數(shù)的單調(diào)性,進(jìn)而利用函數(shù)的基本性質(zhì)來綜合分析與處理,實(shí)現(xiàn)參數(shù)大小關(guān)系的判斷. 解析:由asina-2bsin 2b=4b2-a2+1,可得asina+a2=4b2+2bsin 2b+1. 又由于asina+a2=(2b)2+2bsin 2b+1>(2b)2+2bsin 2b,因此同構(gòu)函數(shù)f(x)=xsinx+x2,x∈R. 因?yàn)閒(-x)=-xsin(-x)+(-x)2=xsinx+x2=f(x),所以函數(shù)f(x)為偶函數(shù). 求導(dǎo),可得f′(x)=sinx+xcosx+2x. 所以當(dāng)x≥0時,f′(x)≥0,則知函數(shù)f(x)在區(qū)間[0,+∞)上為增函數(shù). 由asina+a2>(2b)2+2bsin 2b,可得f(a)>f(2b).又函數(shù)f(x)為偶函數(shù),所以f(|a|)≥f(|2b|),可得|a|>|2b|. 故選擇答案:C. 點(diǎn)評:在解決此類三角函數(shù)問題時,經(jīng)常要通過三角恒等變換,利用一些相關(guān)的關(guān)系加以變形,從而尋找問題的同型,實(shí)現(xiàn)地位同等策略同構(gòu)函數(shù)的目的,進(jìn)而借助函數(shù)的基本性質(zhì)來比較大小. 三角函數(shù)中的不等式證明問題,有時也可以借助代數(shù)關(guān)系式的結(jié)構(gòu)特征,尋找共性,同構(gòu)函數(shù),通過函數(shù)的基本性質(zhì),從函數(shù)的思維視角來解決. 例4在銳角三角形ABC中,A,B,C是該三角形的三個內(nèi)角,試證明:sinAsinBsinC>sinA+sinB+sinC-2. 分析:結(jié)合題目所要證明的三角不等式,以其中一個內(nèi)角的正弦值為主元進(jìn)行恒等變形,通過同構(gòu)函數(shù),利用銳角三角形各內(nèi)角的正弦值的取值情況來確定一次函數(shù)的單調(diào)性,并結(jié)合對應(yīng)的函數(shù)值,巧妙轉(zhuǎn)化思維,綜合利用函數(shù)的單調(diào)性來證明對應(yīng)的三角不等式問題. 證明:要證sinAsinBsinC>sinA+sinB+sinC-2,即證(sinAsinB-1)sinC-(sinA+sinB)+2>0. 同構(gòu)函數(shù)f(x)=(sinAsinB-1)x-(sinA+sinB)+2,x∈(0,1). 而f(1)=sinAsinB-1-(sinA+sinB)+2=(1-sinA)(1-sinB)>0(這里0 結(jié)合sinAsinB-1<0,可知函數(shù)f(x)在區(qū)間(0,1)上單調(diào)遞減. 所以函數(shù)f(x)在區(qū)間(0,1)上恒有f(x)>f(1)>0,則有f(sinC)>0. 因此f(sinC)=(sinAsinB-1)sinC-(sinA+sinB)+2>0. 變形轉(zhuǎn)化,可得sinAsinBsinC>sinA+sinB+sinC-2成立,不等式得證. 點(diǎn)評:在解決以上三角不等式的證明問題時,如果沒有頭緒或無從下手,可以合理改變解題方向,通過題目的條件或結(jié)論的分析與考查,合理拓展思維,借助主元法等其他方法加以巧妙變形與轉(zhuǎn)化,同構(gòu)出與問題有關(guān)的基本初等函數(shù),利用相應(yīng)函數(shù)的相關(guān)知識來尋找與轉(zhuǎn)化解決問題的方法與途徑,實(shí)現(xiàn)問題的巧妙破解. 在破解一些三角函數(shù)的相關(guān)問題時,關(guān)鍵是抓住題目中三角函數(shù)關(guān)系式的結(jié)構(gòu)特征,慧眼識別與尋找同型或共性,特別是結(jié)合三角恒等變形,巧妙抽象,合理同構(gòu)函數(shù),利用共性,將一些不熟知的三角函數(shù)問題轉(zhuǎn)化為與之相關(guān)的其他基本初等函數(shù)問題來分析與處理,不斷增強(qiáng)創(chuàng)新意識、同構(gòu)意識等,提升創(chuàng)新應(yīng)用能力,拓展思維,形成數(shù)學(xué)能力,培養(yǎng)數(shù)學(xué)核心素養(yǎng).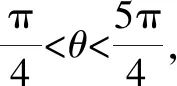
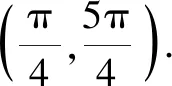
2 求函數(shù)值
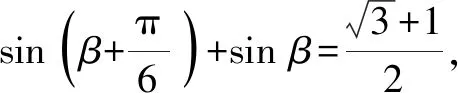
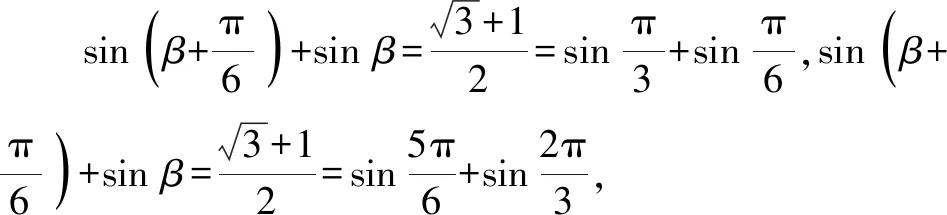
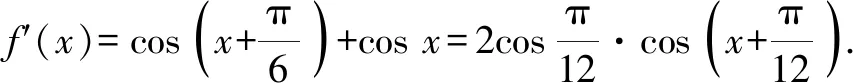
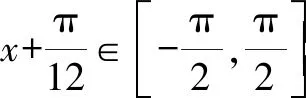
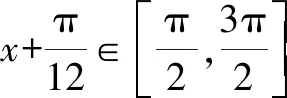
3 大小比較
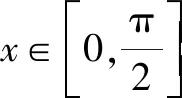
4 不等式證明

