Parameterized monogamy and polygamy relations of multipartite entanglement

Zhong-Xi Shen(沈中喜), Ke-Ke Wang(王珂珂), and Shao-Ming Fei(費少明)

1School of Mathematical Sciences,Capital Normal University,Beijing 100048,China

2Max-Planck-Institute for Mathematics in the Sciences,Leipzig 04103,Germany

Keywords: monogamy,polygamy,concurrence,entanglement of formation

1.Introduction

Entanglement is one of the most remarkable phenomena in quantum mechanics, which is also the most important resources in quantum information processing and communication.[1-4]In recent years, great efforts have been made toward the understanding of the role played by the entanglement in quantum information theory such as quantum teleportation,[5]quantum key distribution,[6]and quantum computing.[7]

An important problem in the theory of quantum entanglement is the quantification of entanglement.[8]The entanglement for bipartite systems has been intensively studied,while the characterization and quantification of multipartite entanglement is far from being satisfied.An essential property of quantum entanglement is that a quantum system entangled with one of the other subsystems limits its entanglement with the remaining ones, known as the monogamy of entanglement.[9,10]Monogamy describes the distribution of entanglement among the multipartite systems.It is an important way to study the structure and properties of multipartite entanglement.In Ref.[11] the authors showed that any entanglement measure given by a strictly concave function of the reduced density matrix for pure bipartite states is monogamous for pure tripartite states.Since the monogamy of entanglement restricts on the amount of information that an eavesdropper could potentially obtain about the secret key extraction, it plays a crucial role in the security of many information-theoretic protocols such as quantum key distribution protocols.[12,13]The monogamy of entanglement has also been widely used in,e.g.,quantum information theory,[14]condensed-matter physics,[15]and even black-hole physics.[16]

Coffman, Kundu and Wootters first characterized the monogamy of entanglement for three-qubit statesρABC,[17]

whereρAB= trC(ρABC) andρAC= trB(ρABC) are the reduced density matrices and?is an entanglement measure.It is shown that not all entanglement measures satisfy such monogamy relations.Although the concurrenceCdoes not satisfy such monogamy inequality, it has been proved that the squared concurrenceC2[18]and the squared entanglement of formationE2[19,20]do satisfy the monogamy relations for multipartite qubit systems.With respect to the inequality(1),the monogamy relations have also been explored for other entanglement measures such as the convex-roof extended negativity (CREN) ～N,[21-23]Tsallis-qentropy,[24-26]R′enyi-αentropy,[27,28]unified entropy,[29,30]and geometric measure.[31,32]

Another important concept is the entanglement of assistance, which is a dual amount to bipartite entanglement measure.It has a dually monogamous property in multipartite quantum systems and gives rise to polygamy relations.As another entanglement constraint in multipartite entanglement, polygamy can be described by assisted entanglement.For arbitrary tripartite systems, Gouret al.in Ref.[33] established the first polygamy inequality by using the squared concurrence of assistanceC2a.For a tripartite stateρABC, the usual polygamy relation is characterized through the following form:

where?ais the corresponding entanglement measure of assistance associated to?.It was later generalized to multiqubit systems by using various assisted entanglements.[24,29,33]For the arbitrary dimensional quantum systems, using entanglement of assistance, general polygamy inequalities of multipartite entanglement were also proposed in Refs.[34-36].In Ref.[37] the author showed that any entanglement of assistance is polygamous but not monogamous, and any faithful entanglement measure is not polygamous.

Recently, generalized classes of monogamy inequalities related to theα-th power of entanglement measures were proposed.In Refs.[38-40], the authors proved that the squared concurrence and the convex-roof extended negativity satisfy the monogamy inequalities in multiqubit systems forα ≥2.It has also been shown that the entanglement of formation(EoF)satisfies monogamy relations whenIn addition, the Tsallis-qentanglement and R′enyi-αentanglement satisfy monogamy relations whenα ≥1.[24,27,39,40]Moreover, the corresponding polygamy relations have also been established.[25,33,35,41]

In this paper, we present the monogamy inequalities in terms of the concurrenceCand entanglement of formationE,we also provide the polygamy inequalities in terms of the concurrence of assistanceCaand the entanglement of assistanceEa.Furthermore,we show that our optimized monogamy and polygamy relations are tighter inequalities than the results in Refs.[38-40,42,43].

2.Tighter monogamy and polygamy relations for concurrence

Let?Xdenote a finite-dimensional complex vector space associated to a quantum subsystemX.Given a bipartite pure state|φ〉ABin Hilbert space?A ??B,the concurrence is given by

for allα ≥2, where the second and third equalities hold whenp= 1 andδ= 1, respectively.Then our results are seen to be tighter than that in Ref.[43].Therefore, our new monogamy relation for concurrence is better than those in Refs.[38-40,42,43].

Example 1 Let us consider the three-qubit state|φ〉ABCin the generalized Schmidt decomposition,[48,49]

Whenl=1/k,μ=1,the lower bound Eq.(25)gives the same result as Eq.(24).Letk=2/3,l=3/2,μ=2,δ=1 andp=2.It can be seen that our result Eq.(22)is better than the result Eq.(25) in Ref.[43] forα ≥2, hence also better than Eq.(24)given in Ref.[42]and Eq.(23)given in Ref.[40],see Fig.1.

Fig.1.From top to bottom,the green thick(black thin,blue dotted and red dot-dashed)line represents the lower bound taken from our previous results(Refs.[40,42,43],respectively).

For a tripartite state|φ〉ABC,the concurrence of assistance(CoA)is defined by[50,51]

For convenience, we denote byCaAB j=Ca(ρAB j) forj=1,2,...,N-1, andCaA|B1B2···BN-1=Ca(ρA|B1B2···BN-1).Similar to the proof of Theorem 1, by using inequality (11) we have the following tighter polygamy relations for the concurrence of assistance.

Letk=4/7,l=7/4,μ=3/4,δ=1,p=11/8.It can be seen that our result Eq.(31)is better than the result Eq.(33)in Ref.[42]for 0<α ≤2,thus also better than Eq.(32)given in Ref.[40],see Fig.2.

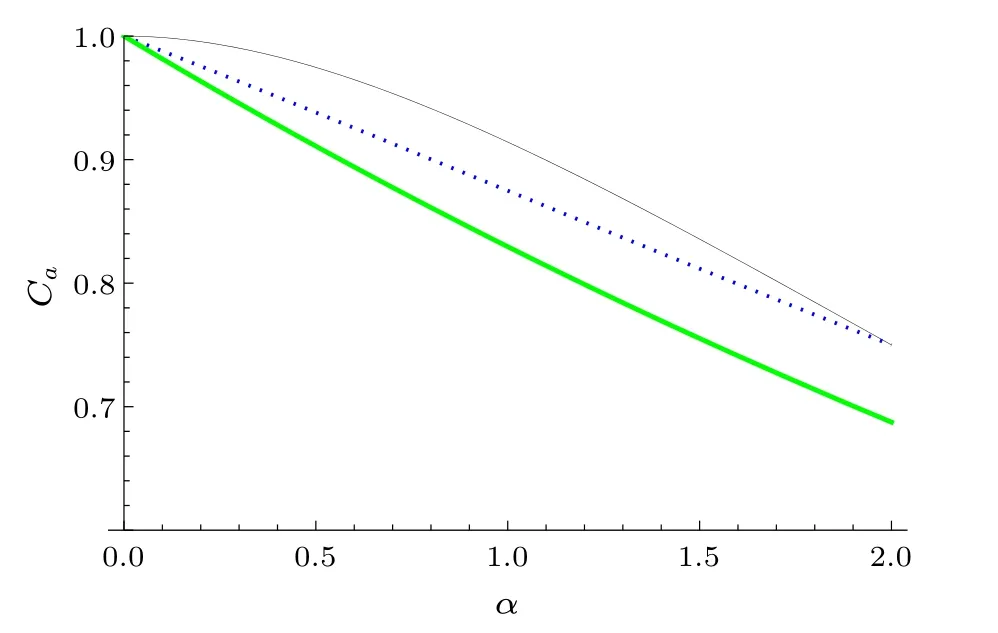
Fig.2.From bottom to top,the green thick(black thin and blue dotted)line represents the upper bound from our result(Refs.[40,42],respectively).

3.Tighter monogamy and polygamy relations for EoF

Let?Aand?Bbem- andn-dimensional (m ≤n) vector spaces, respectively.The entanglement of formation of a pure state|φ〉∈?A ??Bis defined byE(|φ〉)=S(ρA),whereρA=TrB(|φ〉AB〈φ|)andS(ρ)=-Tr(ρlog2ρ).[53,54]For a bipartite mixed stateρAB ∈?A ??B,the EoF is given by

where the first inequality is due to inequality(44),the second inequality is obtained similarly to the proof of Theorem 1 by using inequality (43).The last equality holds since for any 2?2 quantum stateρABi,E(ρABi)=f[C2(ρABi)].

In particular, similar to the case of concurrence, we also have the following tighter monogamy relation for EoF.

Therefore,with respect to inequality(46),whenN=3 we have

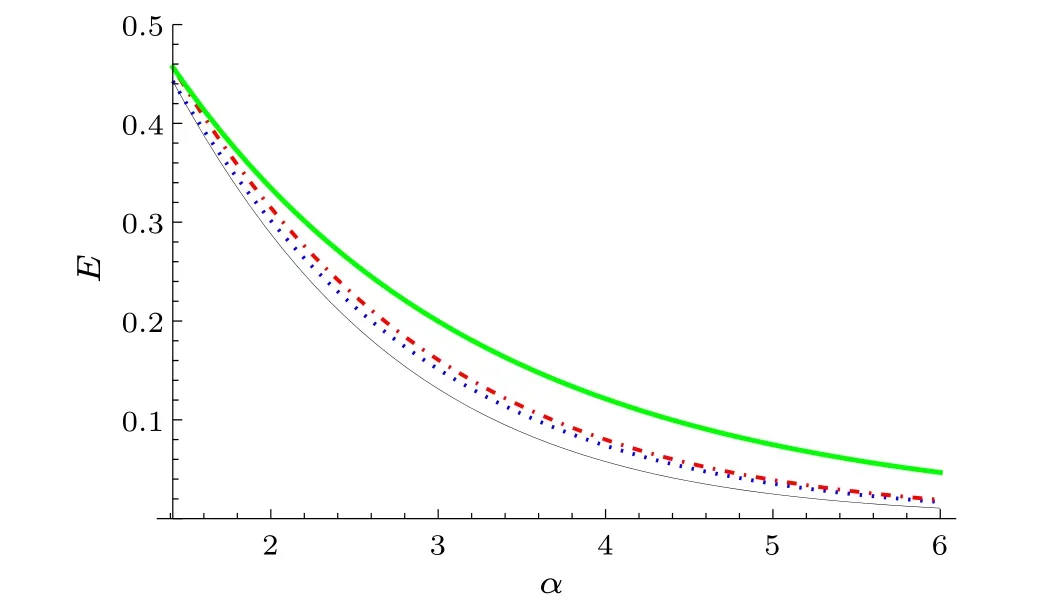
Fig.3.From top to bottom, the green thick (black thin, blue dotted and red dotdashed) line represents the lower bound from our result(Refs.[40,42,43],respectively).

We can also provide tighter polygamy relations for the entanglement of assistance.The corresponding entanglement of assistance(EoA)of a bipartite mixed stateρABis defined by andEaA|B1B2···BN-1=Ea(ρA|B1B2···BN-1).Using the same approach as for CoA,we have the following theorems.

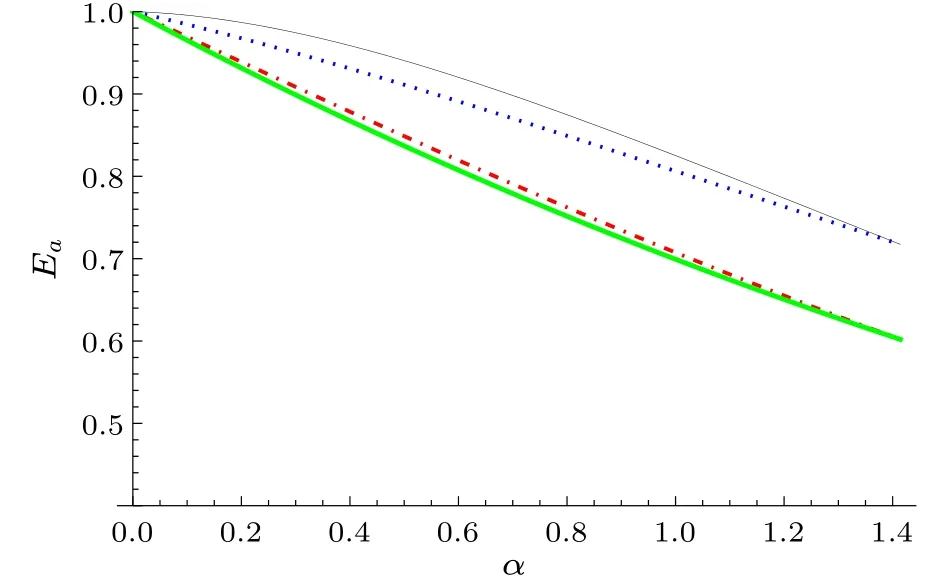
Fig.4.From bottom to top, the green thick (black thin, blue dotted,and red dot-dashed) line represents the upper bound from our result(Refs.[40,42,43],respectively).

4.Conclusions

Entanglement monogamy and polygamy are the essential properties of multipartite qubit systems, which characterize the distributions of entanglement.We have presented monogamy relations related to theα-th power of concurrence and entanglement of formation.We have also provided polygamy relations related to the corresponding entanglement measures of assistance.All the relations we derived are tighter than the previous existing results.These tighter monogamy and polygamy inequalities provide finer characterizations of the entanglement distributions among the multiqubit systems.By using our approach the monogamy and polygamy properties with respect to other entanglement measures such as convex-roof extended negativity, Tsallis-qentanglement and R′enyi-αentanglement can be similarly investigated.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant Nos.12075159 and 12171044),the Beijing Natural Science Foundation(Grant No.Z190005),and the Academician Innovation Platform of Hainan Province.