基于有源電力濾波器的改進型電流控制方法

楊雙雙

（國網天津濱海供電公司，天津 300450）

0 引 言

隨著電力電子技術的迅速發展，電網中使用各類功率開關和非線性負荷設備，導致嚴重的諧波污染出現。通常采用的補償諧波方法是引進有源電力濾波器（Active Power Filter，APF），而抑制諧波模塊則采用LCL濾波器[1-2]。但以網側電流作為反饋設計會使系統穩定性變差，產生較大紋波，損壞功率器件。近來，大量學者提出用逆變側電流設計，以改善系統穩定性差的問題，但整體補償效果依然不佳[3-4]。在此基礎上，針對并聯的APF提出了利用電容電流前置疊加逆變側電流控制的新型策略，以補償系統中的電流，進一步提高APF整體補償精度，同時采用仿真驗證該控制策略的實用和有效性。

1 含有LCL濾波器的APF模型

含有LCL濾波器的APF拓撲結構如圖1所示。Lg、Lc、Cf、Rd分別代表網側濾波電感、逆變側濾波電感、濾波電容以及系統阻尼電阻。其中阻尼電阻為抑制系統諧振的元件。

圖1 含有LCL濾波器的APF拓撲結構

假定系統三相電壓對稱，不計電感寄生電阻，濾波電感為線性，由基爾霍夫電流定律（Kirchhoff's Current Law，KCL）、基爾霍夫電壓定律（Kirchhoff's Voltage Law，KVL）得到系統方程

式中：udc為直流電壓；uc為電容電壓；L1為逆變側電感；L2為網側電感；e為電網電壓；C為濾波電容；i1為逆變側電流；i2為網側電流。根據式（1）建立頻域模型，如圖2所示。

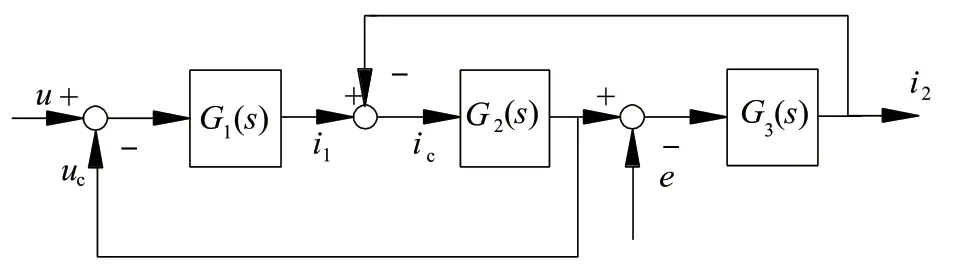
圖2 LCL濾波器模型

2 傳統電流控制策略

2.1 網側電流閉環方法

網側電流閉環方法的控制模型如圖3所示。

圖3 以網側電流作為反饋回路的控制模型

開環傳函G0(s)的計算公式為

式中：Gi(s)為主電路模塊傳遞函數。式（3）可以簡化為

式中：kp為比例系數；ki為積分系數。如果系統開關頻率很大，可用kp表示Gi(s)。

2.2 逆變側電流閉環方法

逆變側電流閉環方法的控制模型如圖4所示。

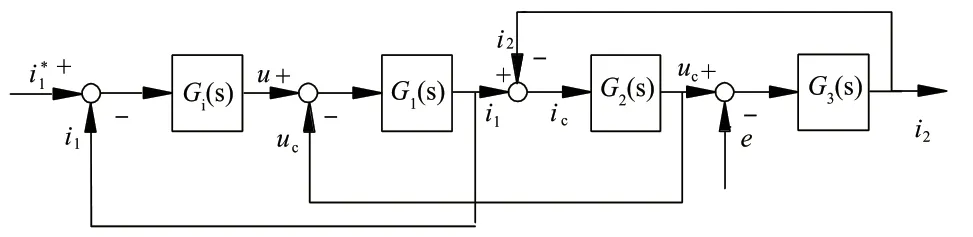
圖4 以逆變側電流作為反饋回路的控制模型

系統開環傳遞函數為

3 含有LCL濾波器的改進控制方法

為提高補償精度，將LCL濾波器電容電流作為前置。首先將LCL濾波器電容電流與指令電流疊加，其次將疊加后的結果減去逆變側電流，最后將結果輸入控制系統產生補償諧波。控制模型如圖5所示。

圖5 引入電容電流前饋的系統控制模型

3.1 開關頻率處諧波

引入電容電流作為前置反饋前，用σ表示衰減比，則由圖4推導出

引入電容電流作為前置反饋后，由圖5推導出

由式（6）和式（7）計算出的系統衰減比沒有明顯變化，證明系統衰減比僅受網側濾波電感與濾波電容的影響。因此，引入電容電流作為前置反饋的方法并未改善諧波對開關頻率的抑制作用[5-6]。

3.2 根軌跡

逆變側電流作為反饋時，系統開環傳遞函數零點、極點數分別為2和3。引入電容電流前饋后，零點分布不變，極點只剩原點位置1個。說明引入前饋后，若系統開環增益不變，其閉環極點會距虛軸更遠，暫態分量衰減更快，系統可以在更短時間達到穩定。

4 仿真研究

利用MATLAB開展仿真，選取6.6 kVA的有源電力濾波器；逆變開關頻率取12.5 kHz；直流側電壓取800 V；電容取2 200 μF；Lc和Lg分別取2.8 mH、0.6 mH；Cf取5 μF；Rd取4 Ω。APF投入系統的時間設置在啟動時間0.04 s之后[7-8]。

應用網側電流和逆變側電流作為反饋回路時，系統的電流波形及補償電流波形如圖6所示。

圖6 系統的電流波形/補償波形

由圖6可知，采用網側電流作為反饋回路時紋波很大，容易損壞功率開關；而逆變側電流作為反饋回路時，紋波較小，能有效保證系統運行的穩定性。

傳統控制策略和新型控制策略下系統側電流諧波分析分別如圖7、圖8所示。

圖7 傳統控制策略下系統側電流諧波分析

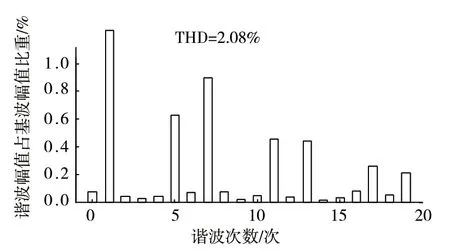
圖8 新型控制策略下系統側電流諧波分析

由圖7和圖8可以看出，未引入電容電流前反饋時系統側總諧波畸變率（Total Harmonic Distortion，THD）為3.12%；引入電容電流前反饋后系統側THD為2.08%。說明引入電容電流前反饋可以抑制系統諧波，降低了系統整體的諧波含量。

5 結 論

文章主要分析了加入LCL濾波器的APF，在采用典型網側電流作為反饋回路和采用逆變側電流作為反饋回路時性能的優劣。在此基礎上，提出了改進策略，通過引入電容電流作為前置回路，并將逆變側電流疊加到閉環控制。該方法能夠進一步優化補償電流的跟蹤效果，從而提高APF的補償精度，抑制諧振峰值，使系統在更短時間達到穩定。