考慮航段復(fù)雜度的機(jī)場(chǎng)終端區(qū)進(jìn)場(chǎng)程序設(shè)計(jì)與評(píng)估

湯榮亮，王子明，王艷軍*①

（1.南京航空航天大學(xué)，民航學(xué)院，南京 211106；2.中國(guó)民用航空華東地區(qū)空中交通管理局江蘇分局，南京 210000）

0 引言

交通運(yùn)輸業(yè)是我國(guó)的重要戰(zhàn)略產(chǎn)業(yè)，高質(zhì)量的交通運(yùn)輸系統(tǒng)能夠在預(yù)期的時(shí)間內(nèi)將人或貨物運(yùn)送到目的地，對(duì)促進(jìn)國(guó)民經(jīng)濟(jì)發(fā)展等具有十分重要的意義。隨著經(jīng)濟(jì)的發(fā)展，無(wú)論是公路交通運(yùn)輸、鐵路交通運(yùn)輸還是空中交通運(yùn)輸市場(chǎng)的運(yùn)輸量持續(xù)增加，在各個(gè)交通運(yùn)輸系統(tǒng)中的擁擠和延誤現(xiàn)象日益嚴(yán)重。交通擁擠會(huì)帶來(lái)巨大的經(jīng)濟(jì)損失并造成嚴(yán)重的環(huán)境污染。為了解決交通擁擠問(wèn)題，一種方法是通過(guò)合理分配交通流等方式最大化利用現(xiàn)有交通系統(tǒng)資源，提高交通運(yùn)輸效率[1-4]。另外一種方式是通過(guò)增加交通系統(tǒng)容量來(lái)適應(yīng)更多的交通運(yùn)輸需求，例如增加高速車(chē)道數(shù)量、新建機(jī)場(chǎng)跑道和航站樓等。隨著航班的持續(xù)增加和空中交通系統(tǒng)容量的限制，機(jī)場(chǎng)和空域變得越來(lái)越擁擠，航班延誤現(xiàn)象日益嚴(yán)重。終端區(qū)空域擁擠已經(jīng)成為航空運(yùn)輸系統(tǒng)的瓶頸之一。終端區(qū)內(nèi)航班擁擠不僅會(huì)導(dǎo)致航班延誤、取消等問(wèn)題，給旅客帶來(lái)不便，更重要的是會(huì)對(duì)運(yùn)行安全造成嚴(yán)重影響。因此，研究如何解決機(jī)場(chǎng)終端區(qū)交通需求持續(xù)增長(zhǎng)導(dǎo)致的空域擁擠和運(yùn)行壓力等問(wèn)題，對(duì)于改善航空運(yùn)輸?shù)倪\(yùn)行效率、提高旅客出行體驗(yàn)都具有重要意義。

空管系統(tǒng)中的點(diǎn)融合系統(tǒng)是一種先進(jìn)的技術(shù)手段，可以將多個(gè)飛行區(qū)的航班點(diǎn)進(jìn)行融合，形成單一的控制區(qū)域。點(diǎn)融合系統(tǒng)是指支持點(diǎn)融合技術(shù)運(yùn)行的基于性能導(dǎo)航（Performance Based Navigation，PBN）空域結(jié)構(gòu)。該系統(tǒng)由一個(gè)融合點(diǎn)和與該點(diǎn)等距（垂直分離）的兩條或多條排序邊組成。將飛行管理系統(tǒng)、水平導(dǎo)航功能與雷達(dá)引導(dǎo)方法相結(jié)合，實(shí)現(xiàn)優(yōu)化多向進(jìn)場(chǎng)交通流排序與間隔管理[5]。點(diǎn)融合系統(tǒng)是民航領(lǐng)域的一項(xiàng)重要技術(shù)，這種技術(shù)可以提高機(jī)場(chǎng)終端區(qū)的運(yùn)行效率和運(yùn)行效益，提高機(jī)場(chǎng)終端區(qū)的安全水平。雖然點(diǎn)融合系統(tǒng)的設(shè)計(jì)有一定的原則，但是當(dāng)前關(guān)于根據(jù)進(jìn)近空域運(yùn)行特征設(shè)計(jì)點(diǎn)融合系統(tǒng)并評(píng)估的研究工作較少，如何結(jié)合機(jī)場(chǎng)終端區(qū)特征，設(shè)計(jì)點(diǎn)融合系統(tǒng)對(duì)提高機(jī)場(chǎng)終端區(qū)的運(yùn)行效率和安全水平、推進(jìn)民航強(qiáng)國(guó)建設(shè)和高質(zhì)量發(fā)展、提高我國(guó)民航產(chǎn)業(yè)的整體競(jìng)爭(zhēng)力和國(guó)際地位等有重要意義。

國(guó)內(nèi)外對(duì)于機(jī)場(chǎng)終端區(qū)的研究主要集中在航班進(jìn)離場(chǎng)排序、空域復(fù)雜度測(cè)算等方面。例如，Pierre 等人[6]提出了一種算法，用于終端機(jī)動(dòng)區(qū)的有效軌跡規(guī)劃；Gianazza 等人[7]比較了幾種機(jī)器學(xué)習(xí)方法，從歷史數(shù)據(jù)中學(xué)習(xí)空中交通管制員工作量的模型；Delahaye 等人[8]提出了一個(gè)基于動(dòng)態(tài)系統(tǒng)的新的空中交通復(fù)雜性指標(biāo)，基于一組雷達(dá)觀測(cè)值（飛行器位置和速度）構(gòu)建了一個(gè)對(duì)這些數(shù)據(jù)進(jìn)行插值的矢量場(chǎng)；Dahlberg 等人[9]提出了一個(gè)混合積分編程框架，用于設(shè)計(jì)終端操縱區(qū)中的飛機(jī)進(jìn)港路線，以保證飛機(jī)在時(shí)間上的分離，輸出的路線構(gòu)成了操作上可行的合并樹(shù)，并保證終端操作區(qū)中的整體交通模式可以被空中交通管制員監(jiān)控；Chevalier 等人[10]在考慮了跑道的配置、機(jī)場(chǎng)的周?chē)h(huán)境和操作限制等因素的基礎(chǔ)上，提出了一個(gè)設(shè)計(jì)離港和進(jìn)港航線的有效設(shè)計(jì)方案；Raúl Sáez García 等人[11]提出了一種混合整數(shù)程序設(shè)計(jì)方法來(lái)計(jì)算飛機(jī)在終端機(jī)動(dòng)區(qū)的進(jìn)港路線，以保證所有在給定時(shí)間段內(nèi)進(jìn)港的飛機(jī)在時(shí)間上的分離，并且飛機(jī)按照最佳的連續(xù)下降運(yùn)行速度曲線和空載推力飛行；王超等人[12]通過(guò)對(duì)終端區(qū)雷達(dá)航跡進(jìn)行分析，研究了空中交通管制行為的特點(diǎn)，討論不同控制策略下的機(jī)頭時(shí)距演化特性和不同相態(tài)下的機(jī)頭時(shí)距演化特性；游錄寶等人[13]研究了點(diǎn)融合系統(tǒng)的概念、設(shè)計(jì)、運(yùn)行與優(yōu)化，并結(jié)合實(shí)際案例對(duì)研究?jī)?nèi)容與方法進(jìn)行驗(yàn)證；謝丹紅等人[14]進(jìn)行了終端區(qū)點(diǎn)融合系統(tǒng)的研究與論述；趙嶷飛等人[15]從交通運(yùn)輸角度，審視空中交通管理實(shí)踐發(fā)展歷程、學(xué)科知識(shí)和研究方法積累過(guò)程；張軍峰等人[16]針對(duì)PMS 的運(yùn)行模式和多個(gè)利益相關(guān)方的需求，構(gòu)建PMS多目標(biāo)排序與調(diào)度模型，提出基于多目標(biāo)的帝國(guó)競(jìng)爭(zhēng)算法，經(jīng)驗(yàn)證得知該算法有良好的實(shí)際應(yīng)用效果。

雖然有關(guān)進(jìn)港離港的排序以及運(yùn)行優(yōu)化的研究已經(jīng)取得非常豐碩的成果，但是將研究中所提出的機(jī)場(chǎng)終端區(qū)運(yùn)行優(yōu)化方法在實(shí)際機(jī)場(chǎng)中進(jìn)行應(yīng)用的案例不多。如何結(jié)合機(jī)場(chǎng)附近空域結(jié)構(gòu)，識(shí)別空域運(yùn)行瓶頸，設(shè)計(jì)適用于機(jī)場(chǎng)空域的點(diǎn)融合系統(tǒng)是需要解決的問(wèn)題。因此，本文深入分析點(diǎn)融合系統(tǒng)在南京祿口國(guó)際機(jī)場(chǎng)的應(yīng)用，構(gòu)建出點(diǎn)融合系統(tǒng)的運(yùn)行效率評(píng)估系統(tǒng)并對(duì)點(diǎn)融合系統(tǒng)的整體運(yùn)行效率進(jìn)行科學(xué)評(píng)估。本文主要貢獻(xiàn)如下：考慮機(jī)場(chǎng)附近航段的結(jié)構(gòu)和流量特點(diǎn)，構(gòu)建航段復(fù)雜度計(jì)算模型，識(shí)別空域運(yùn)行瓶頸；基于所識(shí)別的空域運(yùn)行瓶頸，為南京祿口國(guó)際機(jī)場(chǎng)設(shè)計(jì)了點(diǎn)融合系統(tǒng)，并使用AirTOP 仿真軟件驗(yàn)證了點(diǎn)融合系統(tǒng)的效率。結(jié)果表明，點(diǎn)融合程序可以緩解平均進(jìn)場(chǎng)延誤，同時(shí)降低管制員平均負(fù)荷。

1 基于航段復(fù)雜度的空域運(yùn)行瓶頸識(shí)別

航段的繁忙程度可以描述為動(dòng)態(tài)交通流在靜態(tài)航段結(jié)構(gòu)限制下產(chǎn)生的非線性等復(fù)雜的聯(lián)系。復(fù)雜度表征了局部與整體之間的非線性形式，因此復(fù)雜度的研究可以較好地解決航段繁忙程度的劃分需求。目前，由于復(fù)雜度缺乏統(tǒng)一的定義，針對(duì)航段復(fù)雜度的分析及其繁忙等級(jí)劃分仍然沒(méi)有統(tǒng)一標(biāo)準(zhǔn)。一些學(xué)者將內(nèi)稟復(fù)雜性定義為航空器與空域結(jié)構(gòu)相互關(guān)聯(lián)，反應(yīng)了航空器的無(wú)序性對(duì)復(fù)雜性的影響[17]，或分析扇區(qū)復(fù)雜性與管制員工作負(fù)荷之間的關(guān)聯(lián)并以此作為扇區(qū)劃分的依據(jù)[18]。研究發(fā)現(xiàn)，部分空域結(jié)構(gòu)指標(biāo)和交通流影響指標(biāo)對(duì)交通復(fù)雜度產(chǎn)生影響[19]。基于此研究，本文以航段為視角，按照空域靜態(tài)結(jié)構(gòu)特征和飛行流量動(dòng)態(tài)特性，基于航段的結(jié)構(gòu)和流量特點(diǎn)，構(gòu)建航段復(fù)雜度計(jì)算模型，識(shí)別空域運(yùn)行瓶頸，為點(diǎn)融合系統(tǒng)設(shè)計(jì)提供基礎(chǔ)。

1.1 基于基尼系數(shù)的流量分布評(píng)價(jià)

基尼系數(shù)（洛倫茲系數(shù)）通常用于綜合評(píng)價(jià)居民內(nèi)部收入分配差距水平，現(xiàn)被廣泛應(yīng)用到污染物排放分配、資源配置、水資源利用等領(lǐng)域。基尼系數(shù)計(jì)算如圖1所示，具體公式如下：

圖1 洛倫茲曲線示意圖[20]Fig.1 Schematic of the Lorentz curve

當(dāng)SA=0 時(shí)，基尼系數(shù)GI=0，表明不存在分配差距，SA的值越大，則表明分配差距越大，分配的越不公平，空域內(nèi)流量在時(shí)間和空間的分布越不均勻。因此，基尼系數(shù)可用于評(píng)價(jià)空域內(nèi)流量在時(shí)間和空間分布的均勻性。

1.2 航段復(fù)雜度定義

航段是空中交通運(yùn)輸網(wǎng)絡(luò)中的重要組成部分，如圖2 所示。航段根據(jù)其自身的物理結(jié)構(gòu)，承載并容納了空中交通流量在扇區(qū)中的飛行流量。在保證運(yùn)行安全的基礎(chǔ)上，航段的復(fù)雜程度用由航段構(gòu)成的交通航路航徑的數(shù)量和流經(jīng)該航段的交通流量進(jìn)行描述，其所構(gòu)成的航路航徑數(shù)量越多，交通流量越大，則航段的復(fù)雜度越高。因此，航段復(fù)雜度需要從航段靜態(tài)結(jié)構(gòu)和航班流量分布兩個(gè)維度構(gòu)建。

圖2 航段結(jié)構(gòu)示意圖Fig.2 Schematic of the route leg structure

（1）航段靜態(tài)結(jié)構(gòu)：基于已有空域結(jié)構(gòu)可知，航段作為航路網(wǎng)的組成部分，與其連接的多條航路共同組成航路運(yùn)輸網(wǎng)，其靜態(tài)結(jié)構(gòu)維度可以用首尾兩個(gè)航路點(diǎn)連通度表征。其中，航路點(diǎn)連通度di表示航路點(diǎn)i所連接航段數(shù)量，體現(xiàn)了航路點(diǎn)的聯(lián)通度。聯(lián)通度越高表明該航段在規(guī)劃層面的重要性越高，即擁有更高的預(yù)計(jì)通行量，必然帶來(lái)較高的繁忙度。航路a的連通度可表示為：

（2）航班流量分布：航班流量的大小和分布均勻程度均對(duì)空域的復(fù)雜程度起到?jīng)Q定性作用，因此航班流量分布維度包括流經(jīng)航段流量和航班流量分布不均勻系數(shù)。其中航班流量分布不均勻系數(shù)采用基尼系數(shù)計(jì)算。

航班流量分布不均勻包括時(shí)間和空間上的分布不均勻：

式中：fa,x表示航段a在高度層x上的總流量，1 ≤x≤n；GItime(fa,x)表示在高度層x中，航段a的流量時(shí)間分布的基尼系數(shù)，體現(xiàn)了不同飛行時(shí)間段內(nèi)流量分布的不均勻程度，間隔為5 min；fa表示航段a的總流量；GIleνel(fa)為統(tǒng)計(jì)時(shí)段內(nèi)航段a所有高度層流量空間分布的基尼系數(shù)，反映了航段不同高度層的流量分布不均勻程度。因?yàn)楫?dāng)航班絕對(duì)均勻分布時(shí)，基尼系數(shù)為0，這與實(shí)際運(yùn)行不符，故采用基尼系數(shù)加1進(jìn)行修正。

1.3 航段復(fù)雜度指標(biāo)

鑒于航段與其相鄰的航段間會(huì)產(chǎn)生相互影響，因此需要計(jì)算航段之間相互影響系數(shù)ra,b，且基于航路運(yùn)行的特點(diǎn)，當(dāng)兩航段其中一條為流入航路節(jié)點(diǎn)，另一條為流出同一航路節(jié)點(diǎn)時(shí)，視為兩條航路連通，ra,b值為1。否則，參照碰撞風(fēng)險(xiǎn)與航段夾角知相互影響系數(shù)計(jì)算公式如下：

式中：θ為航段之間的夾角。

航段a與相鄰航段之間的影響程度ra可以表示為：

鑒于不同航空器類(lèi)型和航段流量密度對(duì)于空中交通的運(yùn)行影響程度較大，因此將機(jī)型混雜系數(shù)mixi和航段距離納入航段復(fù)雜度模型。航段a的復(fù)雜度表示為：式中：fa表示在指定時(shí)間段內(nèi)通過(guò)航段a的流量；為目標(biāo)空域內(nèi)所有航段的流量總值；Da表示航段a的距離；D為目標(biāo)空域內(nèi)所有航段的距離總值；ΝH、ΝM、ΝL分別為重型機(jī)、中型機(jī)、輕型機(jī)數(shù)量。

由上式可知，當(dāng)fa為0 時(shí)也為0，表示無(wú)航班流量時(shí)，航段復(fù)雜度為0，這與實(shí)際運(yùn)行相符；當(dāng)fa、da、ra均增大時(shí)也增大，與前文描述的航段復(fù)雜度定義相符，因此綜合考慮了航段的靜態(tài)結(jié)構(gòu)、交通流量等因素，能客觀反映航段之間的相對(duì)復(fù)雜程度。

1.4 航段復(fù)雜度與扇區(qū)復(fù)雜度和飛行程序的關(guān)系

為便于管理空中交通，有關(guān)當(dāng)局（例如空中交通管理部門(mén)）將空域劃分為不同規(guī)則的幾何體，稱(chēng)為扇區(qū)（Sector）。每個(gè)扇區(qū)通常包含多個(gè)航段，并且由一至兩名空中交通管制員負(fù)責(zé)指揮其中的交通。扇區(qū)復(fù)雜度受到空域結(jié)構(gòu)（航段組成）、交通流分布等因素的影響，直接影響管制員的工作負(fù)荷和扇區(qū)容量。本文并未采用扇區(qū)復(fù)雜度分析空域運(yùn)行瓶頸的主要原因在于本文的目的在于識(shí)別進(jìn)近空域中的運(yùn)行瓶頸，進(jìn)而設(shè)計(jì)相應(yīng)的點(diǎn)融合系統(tǒng)。扇區(qū)復(fù)雜度是考慮扇區(qū)內(nèi)所有航段以及管制員指揮下得到的空域運(yùn)行情況評(píng)價(jià)。

飛行程序是預(yù)先定義的飛行路徑，指導(dǎo)飛機(jī)從終端區(qū)空域進(jìn)入點(diǎn)飛行至特定機(jī)場(chǎng)跑道，或從跑道起飛后直至離開(kāi)終端區(qū)的運(yùn)行路徑，旨在確保飛機(jī)有序安全地進(jìn)入和離開(kāi)終端空域。劃設(shè)進(jìn)離場(chǎng)飛行程序的主要目的是使得航班遵循固定的飛行路徑，實(shí)現(xiàn)有序的交通。航段復(fù)雜性是基于飛行程序結(jié)構(gòu)和交通流分布得出的反映實(shí)際運(yùn)行過(guò)程的復(fù)雜性。合理的飛行程序設(shè)計(jì)有助于高效管理交通、增強(qiáng)安全性，并減輕空中交通管制員的工作負(fù)擔(dān)，所有這些都有助于綜合管理復(fù)雜的終端空域。

2 點(diǎn)融合系統(tǒng)設(shè)計(jì)原則及方案

2.1 點(diǎn)融合系統(tǒng)簡(jiǎn)介

傳統(tǒng)的終端區(qū)空域程序設(shè)計(jì)采用將交通流匯聚到跑道的延長(zhǎng)線，而點(diǎn)融合系統(tǒng)設(shè)計(jì)采用單點(diǎn)合并到達(dá)航班流。從合并點(diǎn)開(kāi)始，飛機(jī)通過(guò)固定路徑加入最后進(jìn)近。在合并之前，程序的一部分（排序弧）在必要時(shí)專(zhuān)門(mén)用于路徑拉伸/延遲吸收。這些弧被設(shè)計(jì)成與匯合點(diǎn)等距的“準(zhǔn)弧”，一旦獲得與前一架飛機(jī)所需的間距，就可以通過(guò)沿航段向每架飛機(jī)發(fā)出的單一直接指令來(lái)實(shí)現(xiàn)排序。當(dāng)獲得交通許可時(shí)，飛機(jī)可以在不使用航段的情況下獲準(zhǔn)進(jìn)入合并點(diǎn)。由于飛機(jī)之間間隔的可預(yù)測(cè)變化，管制員在確定進(jìn)場(chǎng)順序和發(fā)布“直飛”指令的時(shí)機(jī)選擇將變得非常簡(jiǎn)單。管制員顯示屏上的簡(jiǎn)單距離標(biāo)記（以合并點(diǎn)為中心的距離環(huán)）足以支持這種運(yùn)行（如圖3所示）。一旦飛向合并點(diǎn)，機(jī)載系統(tǒng)就會(huì)計(jì)算出需要飛行的距離，飛機(jī)可以從航段高度層/高度連續(xù)下降，只需要調(diào)整速度以在航向合并點(diǎn)時(shí)保持間距。

圖3 具有兩個(gè)平行、垂直分離且方向相反的點(diǎn)融合系統(tǒng)設(shè)計(jì)示例[21]Fig.3 Example of a point merge system design with two parallel、vertically separated and oppositel direction points

2.2 點(diǎn)融合系統(tǒng)設(shè)計(jì)原則

標(biāo)準(zhǔn)/通用PBN 設(shè)計(jì)要求適用于任何點(diǎn)融合設(shè)計(jì)，例如最小程序段長(zhǎng)度、轉(zhuǎn)角/最大航跡角變化。點(diǎn)融合設(shè)計(jì)過(guò)程應(yīng)盡早讓所有相關(guān)利益相關(guān)者參與，以下為點(diǎn)融合系統(tǒng)的特定原則：

（1）航路點(diǎn)類(lèi)型：在點(diǎn)融合設(shè)計(jì)中，航路點(diǎn)通常應(yīng)使用轉(zhuǎn)彎預(yù)期（飛越）來(lái)定義。

（2）航路點(diǎn)命名：戰(zhàn)術(shù)航路點(diǎn)尤其是匯合點(diǎn)，應(yīng)使用五個(gè)字母的可發(fā)音名稱(chēng)。

（3）其他交通流：與其他交通流（起飛流，在復(fù)雜空域的情況下從其他附近機(jī)場(chǎng)到達(dá)/起飛）進(jìn)行程序隔離將影響各種程序段的3D定位和尺寸。

（4）排序航段：在可能的情況下，建議使其主要對(duì)稱(chēng)軸與主要風(fēng)向/跑道方向?qū)R（即排序航段垂直于該方向）設(shè)計(jì)點(diǎn)融合系統(tǒng)，盡量減少不利情形的發(fā)生。

（5）水平尺寸：排序航段的長(zhǎng)度以及排序航段與融合點(diǎn)之間的距離，應(yīng)以容量、燃油效率/環(huán)境影響之間的權(quán)衡為指導(dǎo)。

（6）垂直尺寸：雖然排序航段的高度取決于到最后進(jìn)近點(diǎn)的距離和滿(mǎn)足連續(xù)下降的需要，但還可能需要考慮其他當(dāng)?shù)匾蛩兀缈赡軐?duì)過(guò)渡高度的干擾。

（7）融合點(diǎn)和加入最后進(jìn)近：在靠近跑道的進(jìn)近扇區(qū)，尤其是融合點(diǎn)之后，程序設(shè)計(jì)可能會(huì)受到環(huán)境限制的影響。

3 實(shí)例分析

3.1 南京進(jìn)近空域簡(jiǎn)介

南京進(jìn)近空域由中國(guó)民用航空華東地區(qū)空中交通管理局江蘇分局（以下簡(jiǎn)稱(chēng)江蘇空管分局）提供空中交通管制服務(wù)。2020年，南京本場(chǎng)及周邊南通、無(wú)錫、常州、揚(yáng)州、合肥等航班量迅速增長(zhǎng)，南京02、03和04扇區(qū)壓力進(jìn)一步增大，擬調(diào)整02、03和04扇區(qū)的范圍，并在其基礎(chǔ)上增設(shè)06扇區(qū)。06扇區(qū)主要負(fù)責(zé)南京機(jī)場(chǎng)半塔（OF）方向航班進(jìn)離港，以及合肥、鹽城、淮安、徐州、連云港、無(wú)錫、南通、常州、揚(yáng)州等機(jī)場(chǎng)的進(jìn)離港航班。整個(gè)空域調(diào)整后如圖4所示。

圖4 2020年南京進(jìn)近管制扇區(qū)Fig.4 Nanjing approach control sector in 2020

3.2 南京進(jìn)近空域運(yùn)行瓶頸識(shí)別

以祿口機(jī)場(chǎng)進(jìn)場(chǎng)航段和部分進(jìn)近航段為例，參考實(shí)際的管制經(jīng)驗(yàn)選取11 個(gè)需要重點(diǎn)關(guān)注的航段進(jìn)行航段復(fù)雜度的數(shù)據(jù)統(tǒng)計(jì)分析，對(duì)統(tǒng)計(jì)時(shí)間段內(nèi)每個(gè)統(tǒng)計(jì)日同一統(tǒng)計(jì)時(shí)段的復(fù)雜度進(jìn)行均值處理，用于描述各航段的整體復(fù)雜度。以2019 年5 月18 日為例，部分統(tǒng)計(jì)結(jié)果如圖5 和圖6 所示，圖中“6”表示統(tǒng)計(jì)時(shí)間范圍為06:00～06:59，其余類(lèi)推。

圖5 部分航段復(fù)雜度對(duì)比圖Fig.5 Comparison plot of the complexities of selected route legs

圖6 部分航段復(fù)雜度箱型圖Fig.6 Box plots of selected route legs complexities

如圖5 和圖6 所示，不同方向航段的復(fù)雜度值存在較大差異。其中，HFE方向的LEGIV-OREVO和OREVO-NJ114 航段的復(fù)雜度遠(yuǎn)大于其他航段；OF 方向的5 個(gè)航段OF-AKSIG、AKSIG-NJ120、NJ120-NJ118、NJ118-NJ116、NJ116-NJ110 為第二梯隊(duì)，由于該方向航班到達(dá)集中度明顯低于HFE方向，航班流較為平穩(wěn)且順暢，故而5 個(gè)航段復(fù)雜度較為相近且相關(guān)度較高。表1 給出了9 個(gè)重點(diǎn)航段統(tǒng)計(jì)時(shí)間范圍內(nèi)共651 個(gè)統(tǒng)計(jì)時(shí)間段的復(fù)雜度進(jìn)行0 占比、最大值、平均值、非0 平均值、標(biāo)準(zhǔn)差、非0 標(biāo)準(zhǔn)差的統(tǒng)計(jì)，真實(shí)反映了各航段在南京進(jìn)近的作用和角色。

表1 航段復(fù)雜度統(tǒng)計(jì)結(jié)果Tab.1 Results for route legs’complexity statistics

（1）無(wú)論從均值還是最大值來(lái)看，HFE 方向的LEGIV-OREVO 和OREVO-NJ114 航段均保有最大的復(fù)雜度，且未出現(xiàn)無(wú)航班經(jīng)過(guò)的情況。LEGIV-OREVO 為祿口機(jī)場(chǎng)HFE 方向進(jìn)場(chǎng)的主要起始航段，雖然距離較長(zhǎng)（57 km），在僅有4個(gè)主要可用高度層的情況下，承載了南京進(jìn)近60%的進(jìn)場(chǎng)航班，航班流量極為集中，復(fù)雜度最高。OREVONJ114 為L(zhǎng)EGIV-OREVO 的后續(xù)航段，得益于可用高度層數(shù)量上50%的提升，航段復(fù)雜度總體上低于前序航段。而且，因?yàn)楦优R近跑道，航班的高度層配置等已近趨向平穩(wěn)，故而保有較低的標(biāo)準(zhǔn)差。

（2）OF 方向五條航段的復(fù)雜度整體上低于HFE 方向，前四個(gè)進(jìn)場(chǎng)航段在復(fù)雜度分布特征上較為接近，作為進(jìn)近三邊航段的NJ116-NJ110航段的復(fù)雜度取得峰值。NJ116-NJ110 為祿口機(jī)場(chǎng)OF方向進(jìn)場(chǎng)程序三邊，該航段上的航班與HFE 方向進(jìn)場(chǎng)航班呈相對(duì)的運(yùn)行趨勢(shì)，且可用高度層較少，空間狹小，飛行沖突較為突出，致使其復(fù)雜度高于其他四個(gè)航段。值得注意的是，NJ116-NJ110 航段出現(xiàn)0繁忙程度的比例顯著高于其他航段，原因是在OF 方向進(jìn)場(chǎng)航班排序靠前時(shí)往往采取直飛策略并不使用該三邊進(jìn)場(chǎng)程序造成的。

（3）EABAG 以及TAPEN 方向的航班相對(duì)較為分散，航段空閑時(shí)間較多，呈現(xiàn)為穩(wěn)定的低復(fù)雜度狀態(tài)。

綜上所述，南京進(jìn)近空域內(nèi)HFE 和OF 方向航段航班集中，復(fù)雜度高，容易造成擁堵。這與管制員主觀認(rèn)知相符，與實(shí)際運(yùn)行相匹配。因此，在HFE 和OF 進(jìn)場(chǎng)方向應(yīng)用點(diǎn)融合系統(tǒng)，簡(jiǎn)化雷達(dá)管制過(guò)程，減少管制指令，降低管制員和飛行員工作負(fù)荷，改善陸空通話頻道的擁擠，將有效提升空域運(yùn)行安全。

3.3 南京進(jìn)近PMS程序設(shè)計(jì)方案

基于點(diǎn)融合系統(tǒng)的設(shè)計(jì)原則和南京進(jìn)近空域運(yùn)行實(shí)際，提出以下點(diǎn)融合系統(tǒng)設(shè)計(jì)方案，如圖7所示。

圖7 南京進(jìn)近點(diǎn)融合系統(tǒng)設(shè)計(jì)方案Fig.7 Nanjing approach point merge system design program

（1）融合點(diǎn)選取。通過(guò)上文中關(guān)于進(jìn)近空域內(nèi)擁堵點(diǎn)的識(shí)別，選取融合點(diǎn)位于HFE 和OF 方向進(jìn)場(chǎng)軌跡的交匯點(diǎn)，交通流開(kāi)始匯聚整合的定位點(diǎn)作為程序融合點(diǎn)。基于空域環(huán)境，將其高度設(shè)定為1 800 m（6 000 ft）。

（2）排序弧設(shè)定。融合點(diǎn)位置有HFE 和OF 方向兩條進(jìn)場(chǎng)航線，因此為其分配兩條排序弧。每條排序弧分別占用一個(gè)高度層，相鄰高度層之間垂直間隔為300 m，內(nèi)高外低。基于南京祿口機(jī)場(chǎng)終端區(qū)的空域環(huán)境、航線結(jié)構(gòu)和流量分布，外排序弧的高度選擇2 400 m（9 000 ft），內(nèi)排序弧的高度選擇2 700 m（10 000 ft），兩條排序弧之間水平間隔調(diào)整為9 km。

（3）程序參數(shù)。由于南京祿口機(jī)場(chǎng)飛行程序是以PBN 飛行程序?yàn)橹饔贸绦颍瑢?dǎo)航規(guī)范為RNAV1，本文點(diǎn)融合系統(tǒng)方案設(shè)計(jì)的飛行程序?qū)Ш揭?guī)范為RNAV1。點(diǎn)融合系統(tǒng)的角度參數(shù)如下：進(jìn)入變化角α為45°，直飛變化角β為90°，退出變化角γ為0～40°，包圍角δ為70°。內(nèi)排序邊高度為2 700 m、融合點(diǎn)高度1 800 m、內(nèi)外邊距離40 km、邊-融合點(diǎn)距離45 km、內(nèi)排序邊長(zhǎng)度10 km。南京進(jìn)近管制員一般在會(huì)在IAF點(diǎn)之前，將航空器的速度調(diào)整至180 節(jié)。對(duì)于PMS 程序，由于排序邊距離IAF點(diǎn)的距離至少在30 km，設(shè)定PMS方案的內(nèi)排序邊的速度為200節(jié)，融合點(diǎn)的速度為180節(jié)。

3.4 仿真結(jié)果分析

為了驗(yàn)證本文所設(shè)計(jì)的PMS系統(tǒng)的效率和效益，采用計(jì)算機(jī)快速仿真對(duì)比傳統(tǒng)進(jìn)近程序和PMS 程序的效果。計(jì)算機(jī)快速仿真采用AirTOP仿真軟件構(gòu)建計(jì)算機(jī)仿真模型，輸入航班計(jì)劃進(jìn)行快速仿真，對(duì)比兩種程序下的航班延誤和機(jī)場(chǎng)容量。

3.4.1 仿真實(shí)驗(yàn)設(shè)置

（1）實(shí)驗(yàn)場(chǎng)景。在AirTOP 仿真實(shí)驗(yàn)中，南京機(jī)場(chǎng)東向運(yùn)行，使用跑道為06/07，采用的跑道運(yùn)行模式為獨(dú)立進(jìn)近。

（2）航班計(jì)劃。本次仿真實(shí)驗(yàn)面向未來(lái)航班量，即24小時(shí)內(nèi)共403架次進(jìn)場(chǎng)航班。

（3）飛行程序建模。根據(jù)設(shè)計(jì)的進(jìn)場(chǎng)程序進(jìn)行建模。

（4）仿真參數(shù)設(shè)置。計(jì)算機(jī)仿真中，進(jìn)場(chǎng)移交間隔為20 km，連續(xù)兩架進(jìn)場(chǎng)間隔為4 nm。

3.4.2 結(jié)果分析

圖8 展示了點(diǎn)融合程序下進(jìn)場(chǎng)每小時(shí)平均延誤和實(shí)際降落情況，圖9～圖15 展示了不同運(yùn)行方式原始程序下進(jìn)場(chǎng)每小時(shí)平均延誤和實(shí)際降落情況。表2 展示了PMS 程序和不同運(yùn)行方式下的情況對(duì)比，包括一天內(nèi)平均進(jìn)場(chǎng)航班延誤和總的進(jìn)場(chǎng)航班數(shù)量。通過(guò)圖8 可以看出點(diǎn)融合程序下進(jìn)場(chǎng)延誤高峰出現(xiàn)在12:00～13:00，其他時(shí)間延誤水平較低，平均進(jìn)場(chǎng)延誤小于2 min/架次（不包括0:00，12:00～13:00）。通過(guò)圖9～圖15 和表2 可以看出隨著進(jìn)場(chǎng)航班數(shù)量的增加，平均進(jìn)場(chǎng)延誤呈現(xiàn)上升趨勢(shì)，越來(lái)越多的時(shí)段擁有較高的平均延誤。從運(yùn)行方式00～06，進(jìn)場(chǎng)航班數(shù)量從323 增加到508 架次，平均延誤從01 分12 秒增加到07 分51 秒每架。在點(diǎn)融和程序下，進(jìn)場(chǎng)航班數(shù)量534，而平均進(jìn)場(chǎng)延誤僅有3 分34 秒每架次，作為對(duì)比運(yùn)行方式04 進(jìn)場(chǎng)航班數(shù)量為439，平均進(jìn)場(chǎng)延誤為3 分50 秒每架次。點(diǎn)融和程序優(yōu)化了進(jìn)場(chǎng)交通流，保證了運(yùn)行效率，減少了平均進(jìn)場(chǎng)延誤。

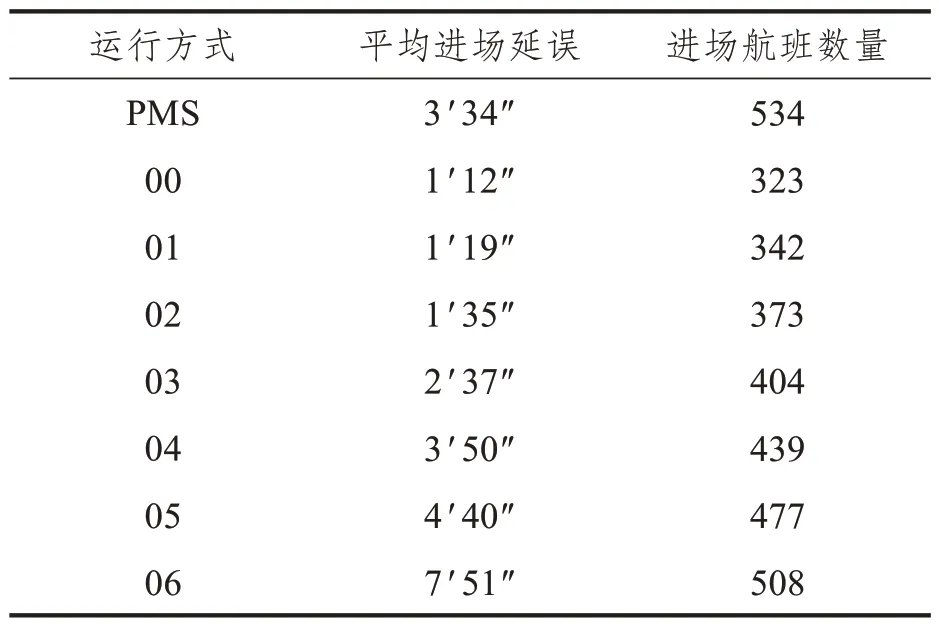
表2 PMS程序和不同運(yùn)行方式下的情況對(duì)比Tab.2 Comparison of the situation under the PMS and different operating mode programs

圖8 PMS仿真進(jìn)場(chǎng)平均延誤和實(shí)際降落圖Fig.8 Average approach delay and actual landing under PMS simulation

圖9 運(yùn)行方式00下平均延誤和實(shí)際降落圖Fig.9 Average approach delay and actual landing under operation mode 00

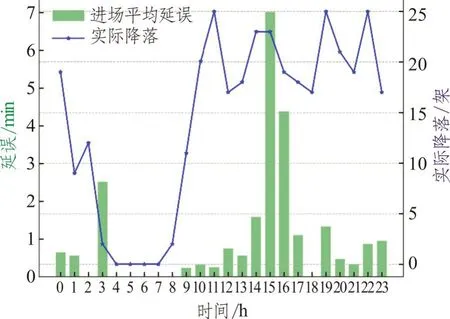
圖10 運(yùn)行方式01下平均延誤和實(shí)際降落圖Fig.10 Average approach delay and actual landing under operation mode 01

圖11 運(yùn)行方式02下平均延誤和實(shí)際降落圖Fig.11 Average approach delay and actual landing under operation mode 02

圖12 運(yùn)行方式03下平均延誤和實(shí)際降落圖Fig.12 Average approach delay and actual landing under operation mode 03

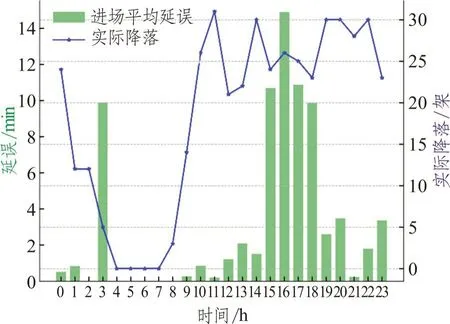
圖13 運(yùn)行方式04下平均延誤和實(shí)際降落圖Fig.13 Average approach delay and actual landing under operation mode 04

圖14 運(yùn)行方式05下平均延誤和實(shí)際降落圖Fig.14 Average approach delay and actual landing under operation mode 05

圖15 運(yùn)行方式06下平均延誤和實(shí)際降落圖Fig.15 Average approach delay and actual landing under operation mode 06

表3 展示了原始程序和點(diǎn)融合程序的情況對(duì)比。通過(guò)使用點(diǎn)融合程序，平均進(jìn)場(chǎng)飛行時(shí)間由20 分50 秒降低到19 分48 秒，平均進(jìn)場(chǎng)延誤從3分11 秒降低到1 分13 秒，平均管制員負(fù)荷從85.93%降低到76.68%。點(diǎn)融和程序有效降低了管制工作負(fù)荷，提高了空域運(yùn)行效率，降低了進(jìn)場(chǎng)延誤。

表3 兩種程序下的情況對(duì)比Tab.3 Comparison of the situation under the PMS and original programs

3.4.3 航段復(fù)雜度對(duì)比

為了驗(yàn)證本文所設(shè)計(jì)的PMS 系統(tǒng)相較于原始程序的航段復(fù)雜性變化，計(jì)算了PMS 程序下的航段復(fù)雜性。如圖16 所示，對(duì)比原始程序和PMS 程序下不同進(jìn)場(chǎng)方向中航段最大平均復(fù)雜度，PMS 程序下航段復(fù)雜度在東邊流量、北邊流量和西邊流量相較于原始程序都有所降低，而在南邊流量有所增加。總的來(lái)說(shuō)，南京進(jìn)近空域中，HFE 方向航段的復(fù)雜度遠(yuǎn)大于其他方向航段復(fù)雜度，使用PMS 程序使得HFE 方向航段的復(fù)雜度降低。

圖16 原始程序和PMS程序下不同進(jìn)場(chǎng)方向中航段最大平均復(fù)雜度對(duì)比圖Fig.16 Comparison of the maximum average complexities of route legs in different approach directions under the original and PMS programs

4 結(jié)論

本文以南京祿口國(guó)際機(jī)場(chǎng)交通基于航段復(fù)雜度的空域運(yùn)行瓶頸識(shí)分析結(jié)果為基礎(chǔ)進(jìn)行了適用于該機(jī)場(chǎng)終端區(qū)的點(diǎn)融合系統(tǒng)的設(shè)計(jì)，并通過(guò)仿真實(shí)驗(yàn)驗(yàn)證了所設(shè)計(jì)的點(diǎn)融合系統(tǒng)相較于傳統(tǒng)運(yùn)行程序的優(yōu)越性，為南京祿口國(guó)際機(jī)場(chǎng)終端區(qū)點(diǎn)融合系統(tǒng)的現(xiàn)實(shí)應(yīng)用提供了強(qiáng)有力的理論研究基礎(chǔ)，為空管系統(tǒng)的高效安全運(yùn)行提供了科學(xué)的指導(dǎo)。主要?jiǎng)?chuàng)新和貢獻(xiàn)如下：

（1）提出了航段復(fù)雜性計(jì)算模型用以識(shí)別終端區(qū)空域運(yùn)行評(píng)價(jià)。本文以航段為視角，按照空域靜態(tài)結(jié)構(gòu)特征和飛行流量動(dòng)態(tài)特性，基于航段的結(jié)構(gòu)和流量特點(diǎn)，構(gòu)建航段復(fù)雜度計(jì)算模型，識(shí)別空域運(yùn)行瓶頸。以祿口機(jī)場(chǎng)進(jìn)場(chǎng)航段為測(cè)試案例，建立了適用于南京祿口國(guó)際機(jī)場(chǎng)終端區(qū)的航段復(fù)雜度指標(biāo)，并依據(jù)該指標(biāo)進(jìn)行了該機(jī)場(chǎng)終端區(qū)的運(yùn)行瓶頸識(shí)別，結(jié)果發(fā)現(xiàn)南京進(jìn)近空域內(nèi)HFE和OF方向航段復(fù)雜度高，容易出現(xiàn)擁堵。

（2）基于空域運(yùn)行評(píng)價(jià)設(shè)計(jì)了點(diǎn)融合運(yùn)行程序，并在南京祿口國(guó)際機(jī)場(chǎng)進(jìn)行了驗(yàn)證。本文基于航段復(fù)雜度計(jì)算模型設(shè)別了空域運(yùn)行瓶頸，以祿口機(jī)場(chǎng)進(jìn)場(chǎng)為例設(shè)計(jì)了點(diǎn)融合系統(tǒng)，并使用AirTOP 軟件驗(yàn)證了點(diǎn)融合系統(tǒng)和傳統(tǒng)運(yùn)行程序。結(jié)果表明，點(diǎn)融合程序可以緩解平均進(jìn)場(chǎng)延誤，同時(shí)降低管制員平均負(fù)荷。

本文研究了基于航段復(fù)雜度的空域運(yùn)行瓶頸識(shí)別分析下點(diǎn)融合系統(tǒng)，未來(lái)可以研究多點(diǎn)融合系統(tǒng)，將兩個(gè)（含）以上的單個(gè)點(diǎn)融合系統(tǒng)并行運(yùn)行，最終匯聚到同一個(gè)航路共用點(diǎn)，從而有效處理多個(gè)方向進(jìn)場(chǎng)交通流的情形。同時(shí)在未來(lái)研究中應(yīng)考慮為點(diǎn)融合系統(tǒng)設(shè)計(jì)復(fù)飛和等待程序，有助于航空器再次加入點(diǎn)融合系統(tǒng)，應(yīng)對(duì)進(jìn)場(chǎng)流量超出點(diǎn)融合系統(tǒng)容量限制的情形。