基于改進(jìn)麻雀搜索算法優(yōu)化SVM的軸承故障診斷研究*

文 征 段俊勇 楊化林

（青島科技大學(xué) 青島 266100）

1 引言

軸承是機(jī)械設(shè)備中的重要組成部分，主要功能是支持機(jī)械旋轉(zhuǎn)體，減少機(jī)械轉(zhuǎn)動(dòng)中產(chǎn)生的摩擦。隨著現(xiàn)代工業(yè)的發(fā)展，機(jī)械設(shè)備需要維持長(zhǎng)時(shí)間的運(yùn)行，對(duì)其整體的強(qiáng)度有了新的要求，這也導(dǎo)致機(jī)械出現(xiàn)故障的概率有了明顯的提高［1］。其中，滾動(dòng)軸承作為機(jī)械設(shè)備的一部分，其重要性不言而喻，據(jù)相關(guān)統(tǒng)計(jì)，工業(yè)機(jī)械的故障大多與滾動(dòng)軸承有關(guān)。因此，如何正確診斷滾動(dòng)軸承故障，對(duì)于降低機(jī)械設(shè)備的維護(hù)成本，減少事故的發(fā)生具有重要意義［2］。

目前，機(jī)器學(xué)習(xí)方法如神經(jīng)網(wǎng)絡(luò)、模糊聚類、粗糙集等技術(shù)不斷應(yīng)用于滾動(dòng)軸承故障診斷領(lǐng)域。曲建嶺等［3］將一維卷積神經(jīng)網(wǎng)絡(luò)（ACNN-FD）應(yīng)用于滾動(dòng)軸承的故障診斷，其故障識(shí)別的準(zhǔn)確率較高，同時(shí)在不同負(fù)載下有良好的泛化能力，但是模型的訓(xùn)練時(shí)間較長(zhǎng)，算法的運(yùn)行效率較低；歐陽(yáng)承達(dá)等［4］提出了一種基于模糊聚類的故障診斷方法，可以對(duì)滾動(dòng)軸承所處的工作狀態(tài)進(jìn)行較為準(zhǔn)確的判斷，加強(qiáng)了故障識(shí)別能力但存在診斷效率低的缺點(diǎn)；陳佳［5］將粗糙集理論作為全新的特征降維技術(shù)，用于軸承故障診斷。優(yōu)化特征參量，實(shí)現(xiàn)滾動(dòng)軸承更為高效的故障診斷，但在算法搜索精度、開拓能力上仍然存在不足。

考慮到上述方法的缺陷，以及采集軸承樣本的困難程度，這些方法的使用在一定程度上有局限性。與這些方法相比，支持向量機(jī)（Support Vector Machine，SVM）在樣本較小的情況下能夠有效完成模式識(shí)別，增強(qiáng)高泛化能力強(qiáng)，防止過度學(xué)習(xí)的出現(xiàn)。許迪等［6］提出了量子遺傳算法優(yōu)化SVM 參數(shù)的分類器，能顯著提高全局收斂能力，但計(jì)算量大且收斂速度慢；李紅月等［7］提出了一種基于改進(jìn)天鷹算法優(yōu)化向量機(jī)的電機(jī)軸承故障診斷方法，該方法具有較好的優(yōu)化時(shí)間效應(yīng)，但在全局搜索能力上有一定的弱勢(shì)。

針對(duì)上述方法出現(xiàn)的問題，本文采用了改進(jìn)麻雀搜索算法（ISSA）優(yōu)化支持向量機(jī)的方法。首先，在基礎(chǔ)的麻雀搜索算法上引入Tent 映射初始化種群，確保初始解盡量分布在求解空間中。然后引入高斯變異，增強(qiáng)種群多樣性，有利于更好地對(duì)潛在區(qū)域進(jìn)行搜索，從而提高搜索速度，加速算法收斂趨勢(shì)的優(yōu)化。最后對(duì)于SVM 的參數(shù)使用ISSA進(jìn)行優(yōu)化，構(gòu)建ISSA-SVM 故障分類模型，搭建實(shí)驗(yàn)平臺(tái)對(duì)上述診斷模型進(jìn)行驗(yàn)證，所得結(jié)果表明該方法的準(zhǔn)確性有較高的提升。

2 ISSA算法

麻雀搜索算法（Sparrow Search Algorithm，SSA）是由Jiankai Xue 等于2020年提出。研究表明，圈養(yǎng)的麻雀存在兩種不同類型：發(fā)現(xiàn)者和追隨者。發(fā)現(xiàn)者負(fù)責(zé)尋找食物，并反饋具體方位，追隨者主要是監(jiān)視發(fā)現(xiàn)者并與之爭(zhēng)搶食物。當(dāng)種群遇到捕食者時(shí)，其中的一個(gè)或者多個(gè)個(gè)體就會(huì)通過聲音向其它麻雀?jìng)鬟f危險(xiǎn)來臨的信號(hào)，確保麻雀種群能夠及時(shí)地避開危險(xiǎn)，繼續(xù)尋找安全的覓食區(qū)域，這樣的麻雀被稱為警覺者［8］。麻雀搜索算法就是利用麻雀的這種生物特性進(jìn)行迭代尋優(yōu)的優(yōu)化算法。

2.1 Tent混沌

SSA 算法在種群進(jìn)行初始化時(shí)具有隨機(jī)性，無(wú)法保證麻雀種群均勻分布，從而降低了后續(xù)的收斂速度。然而，混沌映射由于具有隨機(jī)性、遍歷性和規(guī)律性等特點(diǎn)，在算法的優(yōu)化上應(yīng)用較廣，可以有效地保持種群的多樣性、提高算法的搜索精度和收斂速度［9］。混沌映射的主要類型有三種，分別為L(zhǎng)ogistic 映射、Tent 映射、Circle 映射，單梁［10］等通過嚴(yán)格的數(shù)學(xué)推理，驗(yàn)證了與另外兩種映射相比Tent的遍歷均勻性更好，可以作為混沌序列產(chǎn)生優(yōu)化算法。其表達(dá)式為

2.2 高斯變異

高斯變異（Gaussian Mutation，GM）是利用服從正態(tài)分布的隨機(jī)數(shù)作用于原位置向量產(chǎn)生新位置的優(yōu)化策略。變異算子大多分布在原始位置周圍，相當(dāng)于鄰域搜索在一個(gè)較小的區(qū)域內(nèi)進(jìn)行。這種變異在算法的準(zhǔn)確性和全局搜索能力上都有一定的提升，對(duì)算法的改進(jìn)有著明顯的效果。同時(shí)，遠(yuǎn)離當(dāng)前位置的少數(shù)算子增強(qiáng)了種群的多樣性，有助于更好地對(duì)潛在區(qū)域進(jìn)行搜索，從而提高搜索速度，加速了收斂趨勢(shì)的算法優(yōu)化。高斯變異的表達(dá)式如下所示：

式中：x為原始的參數(shù)值；N( 0'1) 表示期望為0，標(biāo)準(zhǔn)差為1的正態(tài)分布隨機(jī)數(shù)；mutation(x)為高斯變異后得到的數(shù)值。

2.3 算法性能對(duì)比

將優(yōu)化前后的兩種算法進(jìn)行對(duì)比，以檢驗(yàn)優(yōu)化效果。麻雀搜索算法的設(shè)置種群規(guī)模為30，最大迭代次數(shù)為1000。表1 為4 個(gè)不同類型的基準(zhǔn)函數(shù)，其中前兩種為高維單峰函數(shù)，后面的F3 和F4為高維多峰函數(shù)，通過不同函數(shù)檢驗(yàn)優(yōu)化效果。采用的兩個(gè)測(cè)試指標(biāo)分別為平均值（mean）和標(biāo)準(zhǔn)差（std），測(cè)試結(jié)果如表2所示。

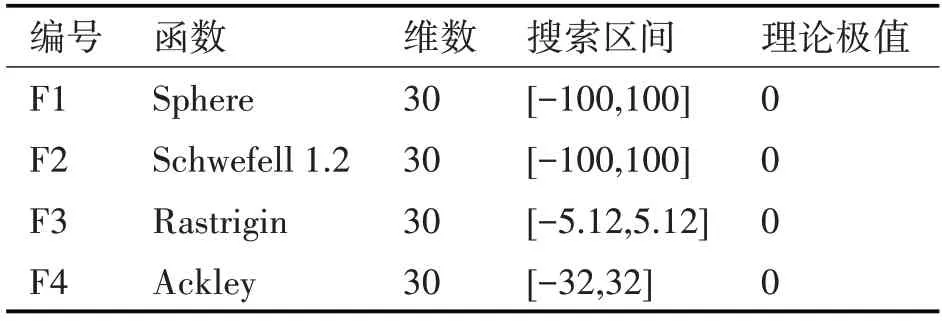
表1 四種基準(zhǔn)函數(shù)

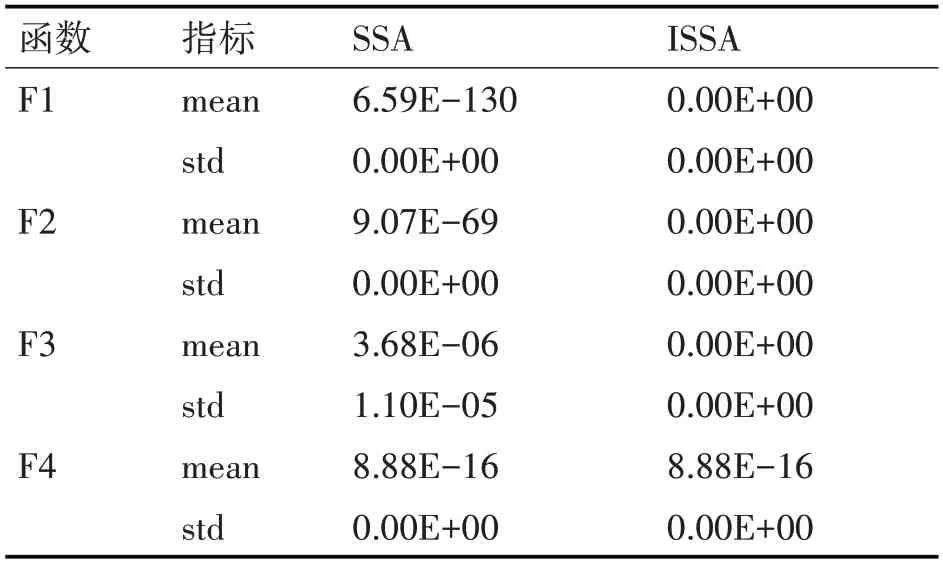
表2 四種基準(zhǔn)函數(shù)測(cè)試結(jié)果

從表2 中可知，單峰函數(shù)F1 和F2，其最優(yōu)值在搜索區(qū)間中的數(shù)量為1。通過對(duì)平均值的分析，我們發(fā)現(xiàn)ISSA 算法能尋找到理論極值0，而SSA 算法只能尋找到一個(gè)接近0的值，ISSA 的尋優(yōu)能力明顯高于SSA。并且std都為0，說明ISSA的尋優(yōu)能力較為穩(wěn)定。

F1 和F2 的收斂曲線如圖1所示，從兩種算法在不同測(cè)試函數(shù)的收斂曲線中可以看出，優(yōu)化后的ISSA 算法相較于之前的SSA 算法在收斂速度上有了較大的提升，優(yōu)化效果較好。

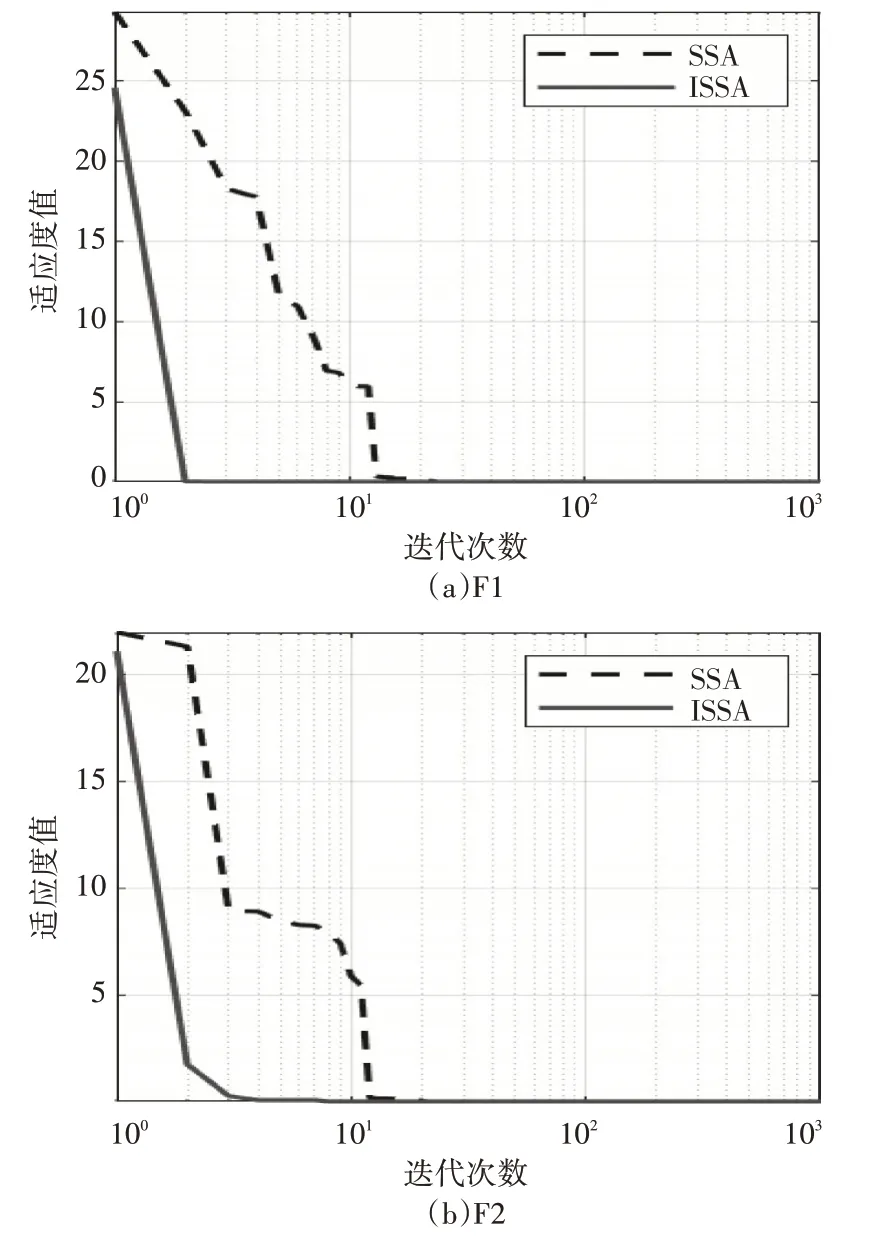
圖1 F1、F2收斂曲線

對(duì)于多峰函數(shù)F3，在圖2 中可以明顯的看到，ISSA在收斂過程中的速度比SSA更快，并且SSA在收斂過程中出現(xiàn)多次局部最優(yōu)值，并且無(wú)法跳出。

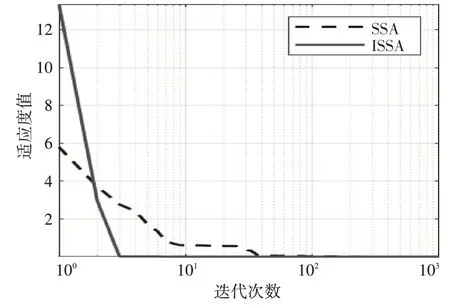
圖2 F3收斂曲線

圖3 為多峰函數(shù)F4 的收斂曲線，其中ISSA 在進(jìn)行迭代后較快就能找到最優(yōu)值，而SSA在迭代幾十次之后才能找到最優(yōu)值，所以通過函數(shù)F4 的測(cè)試，ISSA的尋優(yōu)速度依舊比SSA更快。

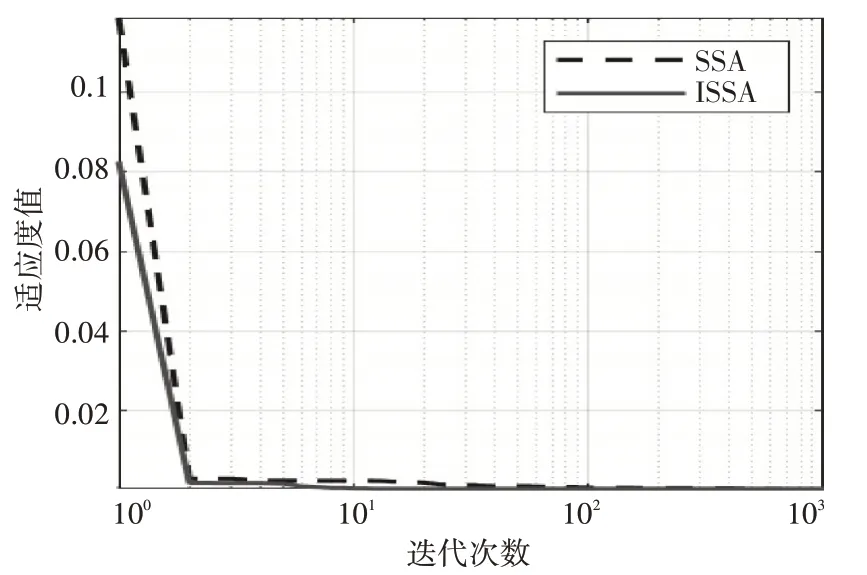
圖3 F4收斂曲線

綜上所述，經(jīng)過4 個(gè)基準(zhǔn)函數(shù)的測(cè)試，ISSA 的尋優(yōu)能力提升明顯，且穩(wěn)定性好、魯棒性強(qiáng)，優(yōu)勢(shì)明顯；同時(shí)，與SSA 相比，ISSA 的收斂速度更快，全局搜索能力更強(qiáng)，能有效避免陷入局部最優(yōu)解，由此證明了ISSA算法的可行性和優(yōu)越性。

3 基于ISSA優(yōu)化的SVM

3.1 支持向量機(jī)（SVM）

作為機(jī)器學(xué)習(xí)的一種，SVM的核心思想是使類別之間的間隔最大化，確保分類有更高的可信度和泛化能力，而靠近邊界的數(shù)據(jù)點(diǎn)被稱為支持向量，這個(gè)方法最早被應(yīng)用于統(tǒng)計(jì)學(xué)［11］。SVM 尋找最優(yōu)分類線時(shí)，當(dāng)線性不可分割時(shí)，引入松弛變量ξ，成為軟間隔支持向量機(jī)，得到以下優(yōu)化問題解決公式。

式中，ω為權(quán)向量，C是懲罰參數(shù)，b為偏移量。

在上式中引入拉格朗日乘子，就將上述尋優(yōu)求解問題轉(zhuǎn)化為對(duì)偶二次規(guī)劃，得到最優(yōu)分類決策函數(shù)：

從而得到非線性最優(yōu)分類決策函數(shù)：

從上式可以看出，在SVM 算法的參數(shù)中，對(duì)其分類性能影響最大的是懲罰參數(shù)（C）和核參數(shù)（g），因此可以通過上述改進(jìn)的ISSA 算法對(duì)其進(jìn)行優(yōu)化，進(jìn)而提高SVM 的分類能力，以實(shí)現(xiàn)最終的故障分類。

3.2 ISSA優(yōu)化SVM流程

圖4 為ISSA 優(yōu)化SVM 流程圖，其具體步驟如下：

圖4 ISSA優(yōu)化SVM模型流程圖

1）讀取訓(xùn)練集，測(cè)試集數(shù)據(jù)，進(jìn)行數(shù)據(jù)預(yù)處理，將訓(xùn)練集和測(cè)試集歸一化。

2）對(duì)ISSA 算法以及SVM 相關(guān)參數(shù)進(jìn)行初始化。

3）經(jīng)過交叉校驗(yàn)，將訓(xùn)練的樣本數(shù)據(jù)進(jìn)行分類。

4）計(jì)算預(yù)警值，以預(yù)警值為依據(jù)，根據(jù)式（1）對(duì)發(fā)現(xiàn)者的位置進(jìn)行更新。

5）根據(jù)式（2）對(duì)追隨者的位置進(jìn)行更新。

6）依據(jù)式（3）更新意識(shí)到危險(xiǎn)的麻雀位置，確保種群安全。

7）計(jì)算麻雀新個(gè)體的適應(yīng)度，并與最優(yōu)新個(gè)體進(jìn)行適應(yīng)度對(duì)比。

依據(jù)上面的流程圖對(duì)迭代次數(shù)進(jìn)行判斷，如果滿足最大迭代次數(shù)，就得到最優(yōu)參數(shù)，進(jìn)而獲得最優(yōu)模型。不滿足，則重復(fù)ISSA 算法中步驟3），直到輸出最優(yōu)解，得到ISSA-SVM模型。

4 ISSA-SVM軸承故障診斷仿真實(shí)驗(yàn)

4.1 實(shí)驗(yàn)設(shè)計(jì)

本文的實(shí)驗(yàn)數(shù)據(jù)來自美國(guó)凱斯西儲(chǔ)大學(xué)的軸承數(shù)據(jù)中心，實(shí)驗(yàn)平臺(tái)如圖5所示。以驅(qū)動(dòng)端的深溝球軸承SKF6205作為實(shí)驗(yàn)對(duì)象，其中的故障軸承是通過電火花加工制作的，系統(tǒng)采樣頻率為12KHz，轉(zhuǎn)速為1797r/min，被診斷的軸承有三種缺陷位置，分別為內(nèi)圈、外圈和滾動(dòng)體［12］。使用VMD對(duì)采集到的信號(hào)進(jìn)行分解和重構(gòu)，提取信號(hào)特征形成特征數(shù)據(jù)集［13］，具體故障分類和樣本編號(hào)見表3。

圖5 實(shí)驗(yàn)平臺(tái)

表3 故障分類及樣本數(shù)

4.2 實(shí)驗(yàn)分析

使用ISSA-SVM、SSA-SVM［14］和PSO-SVM［15］分別對(duì)故障進(jìn)行分類識(shí)別，設(shè)置最大迭代次數(shù)為200。圖6 為ISSA、SSA 和PSO 算法的適應(yīng)度曲線，從圖中可知，使用ISSA 算法優(yōu)化SVM，到達(dá)交叉驗(yàn)證準(zhǔn)確率最優(yōu)值100%的迭代次數(shù)為兩次，與之相比SSA 算法的交叉驗(yàn)證分類準(zhǔn)確率為98.81%，并且SSA 算法更容易陷入局部最優(yōu)，PSO 算法的準(zhǔn)確率為97.77%。

圖6 分類準(zhǔn)確率尋優(yōu)曲線

比較SVM 模型的預(yù)測(cè)測(cè)試集分類和實(shí)際測(cè)試集分類的一致性可以衡量該模型的預(yù)測(cè)準(zhǔn)確，在故障分類的準(zhǔn)確率上SSA-SVM 最高達(dá)到了98.81%（59/60）。而在圖7 中可以看到，ISSA-SVM 模型的分類準(zhǔn)確率更高，達(dá)到100%（60/60），相較之前有著明顯的提升。

圖7 ISSA-SVM預(yù)測(cè)類型分類結(jié)果

在軸承故障的測(cè)試集和訓(xùn)練集不變的情況下，分別將SSA 優(yōu)化SVM 后的診斷模型、ISSA 優(yōu)化SVM 后的診斷模型以及PSO 優(yōu)化SVM 后的診斷模型進(jìn)行訓(xùn)練和測(cè)試，結(jié)果如表4所示。

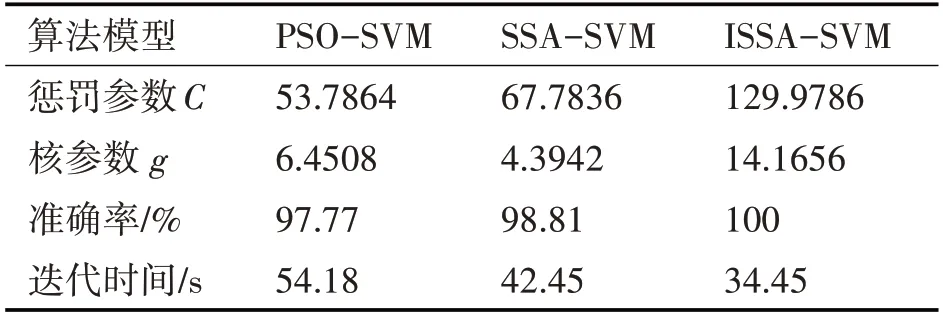
表4 三種分類結(jié)果

從表4 可以看出三種診斷模型中，本文采用的ISSA-SVM 模型的分類準(zhǔn)確率最高，具體數(shù)值為100%，高出SSA-SVM 模型1.19%，與PSO-SVM 模型相比更是有2.23%的提升，分類識(shí)別準(zhǔn)確率上的優(yōu)勢(shì)較大。實(shí)驗(yàn)表明，該算法在SVM 參數(shù)優(yōu)化方面比SSA 和PSO 算法的優(yōu)勢(shì)更加明顯，能較好地提高故障診斷的準(zhǔn)確性。

5 結(jié)語(yǔ)

1）針對(duì)傳統(tǒng)的麻雀搜索算法，利用Tent 映射和高斯變異進(jìn)行改進(jìn)，從而得到ISSA 算法并對(duì)SVM參數(shù)進(jìn)行尋優(yōu)。

2）在軸承的故障診斷中應(yīng)用了ISSA 算法與SVM 算法，并將兩種算法進(jìn)行了結(jié)合運(yùn)用。此外，在軸承正常與故障振動(dòng)信號(hào)的提取上，使用了VMD 算法提取信號(hào)特征，從而獲得良好的特征數(shù)據(jù)集。

3）實(shí)驗(yàn)結(jié)果表明，與SSA-SVM、PSO-SVM 算法模型相比，ISSA-SVM 軸承故障診斷模型的全局搜索能力更強(qiáng)、收斂時(shí)間更短，有較好的分類效果，具有一定的實(shí)際應(yīng)用價(jià)值。