初中數學課堂提問策略初探

王昕

《義務教育數學課程標準（2022年版）》指出，數學教師要選擇能引發學生思考的教學方式，重視單元整體教學設計，強化情境設計和問題提出。問題的提出應引發學生認知沖突，激發學習動機，促進學生積極探究，增強學生解決真實問題的能力，樹立學好數學的自信心，養成良好的學習習慣。因此，教師應合理地提高數學課堂問題的質量和有效性，提升課堂教學質量。

一、激發學習興趣，提高學生思維活躍度

學生只有對數學產生興趣，才能學好數學。在實際教學過程中，教師要想讓學生更加積極地參與到課堂教學中來，最好的方法就是激發學生的學習興趣，提高學生的主觀能動性。教師應針對學生的年齡、理解能力、心理特點去提問，把數學問題與學生感興趣的內容結合起來，活躍課堂氣氛，促進學生主動思考、積極探索，提升課堂教學效果。以蘇科版數學七年級上冊“從問題到方程”一課的教學片段為例。

師：大家最喜歡的中國籃球運動員是誰？

生：姚明。

師：你為什么喜歡姚明？

生：姚明個子高、球技好、訓練刻苦、很幽默……

師：這里有一道關于姚明打籃球的題目，大家愿不愿意嘗試一下？

生：愿意。

例1 著名籃球明星姚明在一場NBA籃球比賽中24投14中，得到28分，其中三分球4投3中。請問姚明兩分球投中多少個？（籃球知識：籃球比賽中罰球投中一個得一分。）

【設計意圖】前兩個問題看似與本節課無關，實際上是針對七年級學生的心理特點和興趣愛好，調動學生學習的積極性，讓學生對例1產生濃厚的興趣，提升學生思維活躍度，便于學生在解題時充分地開動腦筋，思考出正確的解題方法。

二、類比學習內容，構建完整知識體系

類比思想是通過兩個研究對象屬性、特征、關系、形式等方面的類似之處，推斷出它們在其他方面也可能存在類似的一種推理方法。類比思想是將已經學習的知識與即將探索的新知識聯系起來的一種重要的學習思想。在教師精心設計的提問中，學生不僅探究了新的知識，同時也對已學的知識進行了回顧，在提高學習能力的同時，也構建了一個完整的知識體系，并在學習過程中不斷完善、優化。以蘇科版數學八年級下冊“矩形、菱形、正方形”一課的教學片段為例。

師：我們知道，矩形、菱形都是特殊的平行四邊形，它們之間存在著一定的聯系，請同學們回顧矩形的第一個判定方法。

生：有一個角是直角的平行四邊形是矩形。

師：那么請大家猜想一下菱形的第一個判定方法是什么？

生：一組鄰邊相等的平行四邊形是菱形。

師：很好。下面誰來回顧一下矩形的第二個判定方法。

生：三個角是直角的四邊形是矩形。

師：為什么是三個角，而不是四個角？

生：如果三個角是直角，那么第四個角一定是直角。

師：請大家猜想一下菱形的第二個判定方法是什么？

生：四條邊都相等的四邊形是菱形。

師：這個猜想是否正確，我們嘗試來證明一下。（證明過程略。）

師：矩形的第三個判定方法是什么？

生：對角線相等的平行四邊形是矩形。

師：類似的，同學們猜想一下菱形的第三個判定方法是什么？

生：對角線互相垂直的平行四邊形是菱形。

師：同樣的，我們來證明這個猜想的正確性。（證明過程略。）

【設計意圖】本節知識的理解對學生來說是比較困難的，因為需要掌握的定義、定理很多。如果教師能通過問題將前后的知識點結合起來，讓學生掌握它們之間的聯系與區別，便能方便學生更好地理解知識的內涵。在滲透數學思想的同時，也幫助學生更好地構建完整的學科知識體系。

三、引導探究思路，培養良好學習方法

在初中階段的學習中，很多學生感到數學比較難學，特別是在一些有難度的章節中，某些知識點更不容易理解和掌握。這時候往往需要教師指導學生去探索，需要教師根據實際教與學的情況設計有梯度的問題，通過這些問題給學生思考的臺階。問題的設計要由易到難，從學生容易接受的問題開始，一步一步地扶著學生走上臺階，不怕臺階多，關鍵要讓學生踩上來、踩得對、踩得穩。問題的設計還要環環相扣，讓學生從中發現某種聯系和規律，發現突破難點的關鍵所在。這些問題的設置可以引導學生探索正確的思路，讓學生學會思考，循序漸進地掌握知識，感受到學習數學的成就感，最終達到學會學習、善于學習、樂于學習的目的。以蘇科版八年級下冊“圖形的旋轉”一課的教學片段為例。

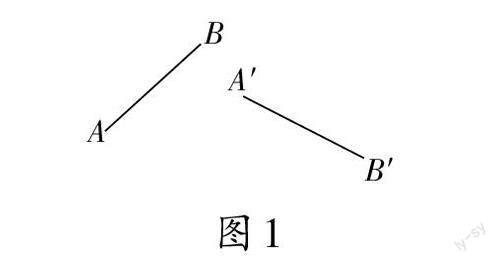
例2 如圖1，畫出AB繞點O旋轉后，線段AB的對應線段是A′B′，試確定旋轉中心點O的位置。

師：同學們，如果我們不能馬上想出解題的方法，那么大家可以猜想一下旋轉中心O的位置大概在哪里？在你認為最可能的地方先畫一個點找找感覺。

生：大概在線段AB 、A′B′的下方。

師：你認為你畫的這個旋轉中心要滿足什么樣的條件？

生：到點A和點A′的距離相等，到點B和點B′的距離相等。

師：為什么？

生：如果這個點是旋轉中心，那么對應點到旋轉中心的距離相等。

師：你能找出到A、A′兩點距離相等的點嗎？

生：在線段AA′的垂直平分線上。

師：你能找出到B、B′兩點距離相等的點嗎？

生：在線段BB′的垂直平分線上。

師：你能找出同時滿足上面兩個條件的點嗎？

生：線段AA′的垂直平分線與線段BB′的垂直平分線的交點。

師：那么你能確定旋轉中心點O的位置了嗎？

生：可以。

【設計意圖】本節課學生已經學習了如何畫已知圖形繞某個點旋轉一定的角度得到的對應圖形，但對由已知圖形和對應圖形找旋轉中心還是感到比較困難的。因此，教師可以先讓學生進行猜想，再通過設置問題串讓學生逐步找到突破口。這樣的過程不僅幫助學生解決了問題，而且還展示了解決問題的正確思考方式，讓學生掌握正確的學習方法。

在數學課堂教學中，許多教師的教案上并沒有細化到每一次提問，課堂上經常出現為了提問而提問，提出的問題沒有針對性的現象，不少提問沒有對教學產生有效的作用，脫離學生的實際。其實，課堂教學中的每一次提問都很重要，只有提高課堂教學中提問的技巧，才能使數學課堂教學更高效，從而促進學生核心素養的生成和發展。