帶輔助信息的復合分位數回歸模型的估計

楊左正,何幫強

(安徽工程大學 數理與金融學院,安徽 蕪湖 241000)

Koenker等[1]最早提出分位數回歸模型,相對于均值回歸模型在處理極端數據時更加穩健。在多個分位數水平下回歸可以得到更加全面的信息。分位數回歸已經廣泛應用于經濟、管理、咨詢、金融、醫學等領域。復合分位數回歸最早由Zou等[2]提出,是傳統分位數回歸理論方法的擴展。這一模型綜合利用多個分位數下的回歸信息,因此能提高估計的有效性。本文考慮一般的線性模型:

式中,Yi?R表示響應變量;Xi?Rp表示p維的協變量;β?Rp表示p維的未知參數;εi表示隨機誤差項。假設隨機誤差項εi的累計分布函數為F(·),概率密度函數為f(·)。對給定常數K,定義0<τ1<τ2< …<τK<1,構造bτk=inf{u:F(u)≥τk},k=1,…,K。本文考慮一組獨立同分布的樣本:(Xi,Yi),i=1,…,n。由此我們可以定義β的復合分位數估計:

式中,ρτk(u)=u(τk-I(u<0)),I(·)為示性函數。 由于可以從多方面搜集信息,數據收集時可能會獲得某些信息,這些輔助信息中蘊藏了某些總體信息,可以用來提高估計量的有效性。文獻[3-5]研究了在輔助信息下的回歸模型的估計。Tang等[6]首次將輔助信息引入分位數回歸模型,結論證實了輔助信息的引入可以增加估計的有效性。之后又有很多學者對輔助信息下分位數回歸模型進行擴展。LYU 等[7]利用經驗似然對這一模型進行了研究。Shen等[8]利用懲罰經驗似然對缺失數據下此模型進行研究。范國良等[9]研究了帶缺失數據和輔助信息的傳統分位數回歸模型。Zhao等[10]利用經驗似然法對復合分位數回歸進行了處理。然而,目前為止,將輔助信息引入復合分位數回歸模型的理論還沒有被系統地提出。

在本文中,我們將輔助信息引入到復合分位數回歸模型中。分別考慮輔助信息參數已知和未知的情況,利用經驗似然法得到輔助信息的自適應權重,并將其引入到復合分位數回歸方程中,得到目標未知參數的估計量及其漸近分布。可以證明,引入輔助信息可以有效提高復合分位數回歸估計的有效性。

1 方法與結論

本文考慮帶輔助信息E[g(Zi,θ)]=0的情況。其中θ?Rd為d維參數,Zi表示一般的可觀測的量,g(Zi,θ)?Rr是一個r維函數,且r≥d。我們利用經驗似然法獲得關于輔助信息E[g(Zi,θ)]=0的數據權重:

利用式(3)計算出的ωi(θ)可以得到帶輔助信息的β的復合分位數回歸估計:

注意到輔助信息函數中的參數θ有已知和未知兩種情況,需要分別考慮。

1.1 θ已知時β的估計

首先考慮θ已知的情況,此時θ由θ0表示。對式(3)利用Lagrange乘子法,可得:

其中,λθ0滿足:

由式(4)、(5)可得θ已知時的輔助信息下的復合分位數估計:

記Σ(θ0)=E[g(Zi;θ0)gT(Zi;θ0)],ψτ(r)=τ-I(r<0)。gim為g(Zi;θ0)第m個位置上的量,m=1,…,r。Xir為p×r維矩陣且每一列都是Xi。令γkm(Xi)表示關于Xi的條件協方差函數,具體表達式為γkm(Xi)=cov(ψτk(εi-bτk),gm(Zi;θ0)|Xi)。令Λkm=E{Xiγkm(Xi)},Λk=(Λk1,Λk2,…,Λkr)為p×r維矩陣。

為了給出定理,需要先提出幾個基本假設條件:

C1:輔助信息中的觀測量Zi,i=1,…,n獨立同分布,且(Yi,XTi)T?Zi。

C2:存在θ0滿足E[g(Zi;θ0)=0,且矩陣Σ(θ0)為正定矩陣。在θ0的鄰域內連續,且矩陣滿秩。存在一個函數Hij(Z)使得在θ0鄰域上的θ滿足≤C1< ∞,其中,i=1,…,r;j=1,…,d。

C3:Yi|Xi=x的條件分布在Xi的定義域內連續,其密度函數f(·;x)連續并且在給定的τk分位數上遠離0和∞。

C6:ε的分布函數和密度函數分別為F(·)和f(·)。對于任意的p維向量δ有:

條件都是一般的,其中條件C1參考了文獻[6]的條件A0,說明了輔助信息觀測量向量不僅可以包含回歸分析中的響應變量和協變量,也可以包含額外的量,體現出本文輔助信息的普適性。條件C2參考了文獻[11]有關經驗似然方法的條件,使經驗似然方法可行。條件C3、C4是分位數回歸可行的最基本的條件。C5、C6是文獻[2]提出的復合分位數回歸可行的條件。

定理1 當θ已知,條件C1~C6成立時,并且β是參數真值,有:

式(2)的漸近方差為:

由于C和Σ(θ0)均為正定矩陣,則在利用輔助信息后,1的方差減小了

1.2 θ未知時β的估計

由于θ未知,就需要先估計θ,本文利用參考文獻[11]的方法,當θ使式(3)達到最大時為θ的估計,即=arg maxθL(θ)。則有:

其中,λ滿足:

則可得在θ未知時,輔助信息下的復合分位數估計:

定理2 當θ未知,條件C1~C6成立時,并且β是參數真值,有:

其中,

由于B是非負定矩陣,故2的漸近方差減少了但是2的漸近方差比1的要大。因此,加入輔助信息可增加估計的有效性,且θ已知時的估計量1更加有效。

由于所構造的復合分位數回歸估計量的漸近方差較為復雜,直接估計會比較困難。故本文采用自助法進行估計,步驟為:利用原始樣本(Xi,Yi),i=1,…,n進行重抽樣得到新樣本(X*i,Y*i),i=1,…,n,再利用新樣本計算得出新估計*。重復上述過程M次,可以得到一組估計*(b),b=1,…,M。由自助法原理可知,自助法估計量的抽樣分布可以用來估計本文的復合分位數回歸估計量的抽樣分布。

2 數值模擬

我們采用如下模型:

其中,(φ0,φ1,φ2)=(0,1,2);ui有兩種案例:第一種ui~N(0,1);第二種ui服從自由度為2的T分布。采用的原始樣本量為N=5 000,由于復合分位數回歸計算量遠大于最小二乘回歸估計,為了減少計算量,只抽取n個樣本進行回歸,其中n?N。總樣本可以作為輔助信息,以此來考察帶入輔助信息是否有助于提高估計的有效性。

本模擬中,(x1,x2)由二變量正態分布N(μ,Σ)產生,其中,μ=(0,0)T,Σ11=Σ22=1,Σ12=Σ21=0.6。在復合分位數回歸中使用等間距分位數,k=1,…,K,K=19。首先按照要求取得樣本量為N=5 000的樣本,并利用其進行最小二乘回歸估計,可得(φ0,φ1,φ2)的估計值則我們可以構造輔助信息函數g(Zi,φ)=(1,x1i,x2i)T(yi-φ0-φ1x1i-φ2x2i),并將其帶入到回歸函數中進行計算。同時也進行相應的不帶入輔助信息的估計。分別采取不同的樣本值n=30,60,100,每次實驗重復500次,自助法重抽樣次數M=200。 模擬計算得到不帶入輔助信息的復合分位數回歸估計的平均均方誤差CQR-MSE,帶入輔助信息的復合分位數回歸估計的平均均方誤差CQREL-MSE,以及帶入輔助信息的復合分位數回歸估計95%置信區間的平均覆蓋率CP。數值模擬結果如表1所示。由表1結果可知,模擬結果證實了加入輔助信息可以提高復合分位數回歸估計的有效性,并且自助法執行區間覆蓋率接近于真實水平95%。

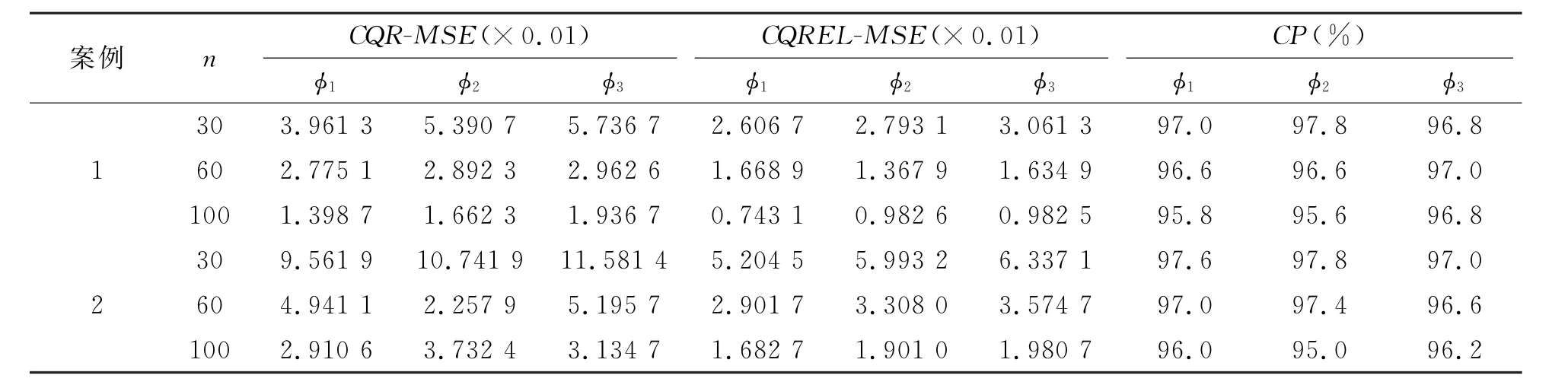
表1 數值模擬結果

3 定理的證明

引理1 在條件C1~C6成立時,有:

證明類似于參考文獻[12]易得,引理1成立。

定理1的證明由式(5)和引理1可得:

則可得:

由式(9)、(10)可得:

下面我們計算cov(Wk,Wk′)的值,其中k,k′=1,…,K。通過矩陣變換可得:

其中,gim為g(Zi;θ0)第m個位置上的量,m=1,…,r。Xir為p×r維矩陣且每一列都是Xi。令Λk2,…,Λkr)為p×r維矩陣,利用大數定律可得:

其中,Ξi,i=1,2,3,4為依次定義的協方差。

由Cramér-Wald device和中心極限定理可得:

Σ是一個方差矩陣,則:

由文獻[2]定理2.1的證明,可得:

由于n Ln是凸函數,(u1,…,uk,δ)可以最小化n Ln,則:

則定理1得證。

定理2的證明由于(λ,)可解式(7),類似于文獻[11]引理1和定理1的證明可得:

并且注意到:BΣ(θ0)B=B。

類似于定理1的證明,可得:

剩余的證明過程類似于定理1,可得:

則定理2得證。

3 結束語

在大數據時代,獲得某些輔助信息是很常見的現象。本文系統地研究了如何將這些輔助信息引入到復合分位數回歸模型中。對輔助信息函數參數已知和未知兩種情況分別進行考慮,利用經驗似然法得出輔助信息的自適應權重,將其帶入原有的回歸方程進行計算,得出了相應的統計量,通過對比發現輔助信息的引入可以使得估計結果更加有效。