彭賽列閉合定理及其應用
王正勇
(如皋市搬經中學,江蘇 如皋 226561)
彭賽列(Poncelet)閉合定理曾幾度出現在高考題中,令很多考生不知所措.筆者現將彭賽列閉合定理進行簡單梳理,并用初等方法由特殊到一般、由具體到抽象地給予介紹,最后給出彭賽列閉合定理在高考中的應用.
1 彭塞列閉合定理的特殊情形
定理1(拋物線與圓)已知拋物線E:y2=2px(p>0)和圓M:(x-m)2+y2=r2(m>0,r>0),過拋物線E上任一點A作圓M的兩條切線,分別與E交于B,C兩點,若滿足r2=2p(m-r),則直線BC與圓M相切.
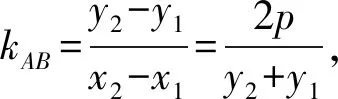
整理,得2px-(y1+y2)y+y1y2=0,經檢驗,當x1=x2時也滿足.
綜上,直線AB的方程為2px-(y1+y2)y+y1y2=0.
同理可得,直線AC的方程為
2px-(y1+y3)y+y1y3=0,
直線BC的方程為2px-(y2+y3)y+y2y3=0.

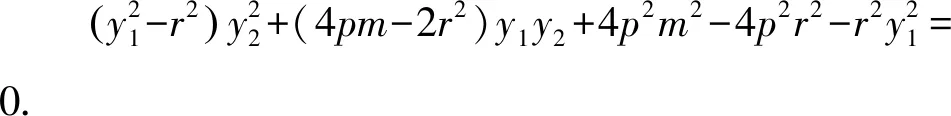


由r2=2p(m-r),得2r2-4pm=-4pr.
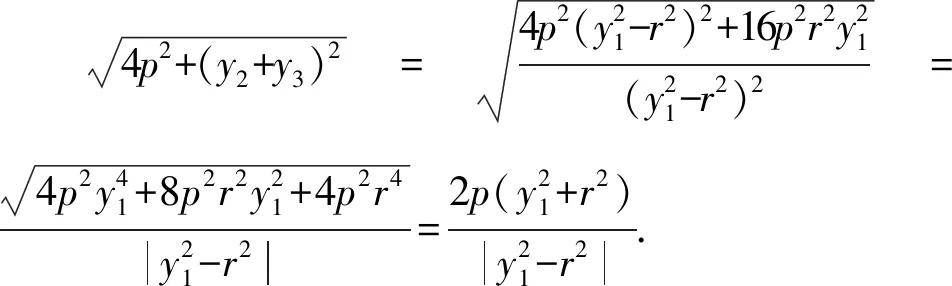
由r2=2p(m-r),得
4p2m2-2pmr2-4p2r2=2pm(2pm-r2)-4p2r2=2pm·2pr-4p2r2=2pr(2pm-2pr)=2pr3.故
即直線BC與圓M相切.
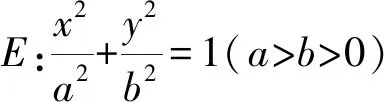
證明設A(acosθ1,bsinθ1),B(acosθ2,bsinθ2),C(acosθ3,bsinθ3),則直線AB的方程為
因為AB與圓x2+y2=r2相切,所以
整理,得
同理,由AC與圓x2+y2=r2相切,有

b2[a2b2+(a2-b2)r2]x1x+a2[a2b2-(a2-b2)r2]y1y+a2b2[a2b2-(a2+b2)r2]=0.
直線BC與圓x2+y2=r2相切的充要條件是
=r.
①
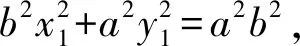
所以①式恒成立的充要條件是
b[a2b2+(a2-b2)r2]=a[a2b2-(a2-b2)r2].

定理3(圓與圓)設A為圓E:x2+y2=R2(R>0)上任一點,過點A作圓M:x2+y2=r2(r>0)的兩條切線,分別與圓E交于B,C兩點,則直線BC與圓M相切的充要條件是R=2r.
這是定理2中a=b的情形,類似可證.
2 彭賽列閉合定理的一般情形
定理4平面上給定兩條圓錐曲線,若存在一封閉多邊形外切其中一條圓錐曲線且內接另一條圓錐曲線,則此封閉多邊形內接的圓錐曲線上每一個點都是滿足這樣(切、內接)性質的封閉多邊形的頂點,且所有滿足此性質的封閉多邊形的邊數相同.
注最簡明的彭賽列閉合定理表示為:一個三角形外接于一個圓,內切于一個圓,則外接圓可以有無數個內接三角形滿足其內切圓為上述的同一個.兩條圓錐曲線都是圓的情形如下.
定理5 設C1和C2是兩個圓.過C1上一點P0作C2的切線,交C1于另一點P1;再過P1作C2的另一條切線,交C1于另一點P2;如此反復,得到C1上的一系列點Pi,i=0,1,2,….如果有自然數n≥3,使得Pn=P0,證明:對于C1上任一點Q0,按上述方式得到Q1,Q2,…,Qn,也有Qn=Q0.
定理中,n=3時的情形如圖1,n=4時的情形如圖2.
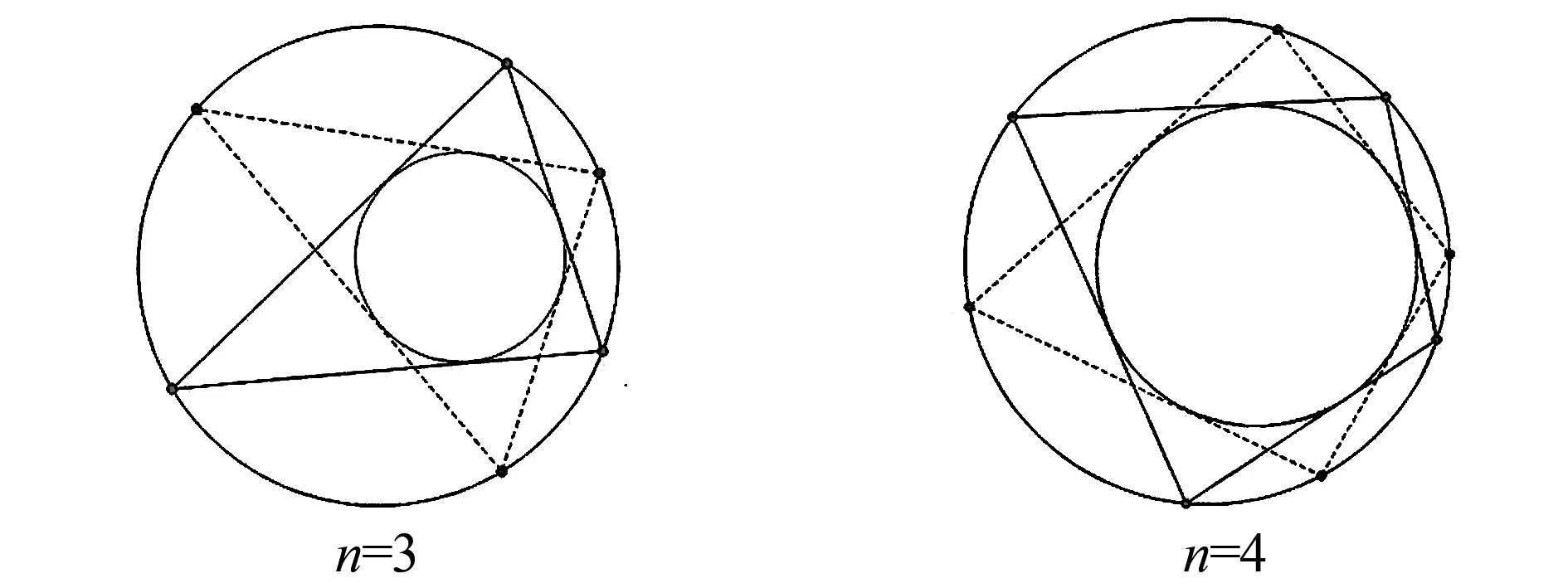
圖1 n=3時的彭賽列定理 圖2 n=4時的彭賽列定理
3 在高考中的應用
通過上文的證明過程可知,以彭賽列閉合定理為背景的試題,屬于“雙切線問題”,解題的關鍵步驟是:表示出兩條切線的方程,利用“同構法”求第三條直線的方程,利用點到直線的距離進行驗證.
應用1拋物線C的頂點為坐標原點O,焦點在x軸上,直線l:x=1交C于P,Q兩點,且OP⊥OQ,點M(2,0),且⊙M與l相切.
(1)求C,⊙M的方程;
(2)設A1,A2,A3是C上的三個點,直線A1A2,A1A3均與⊙M相切,判斷直線A2A3與⊙M的位置關系,并說明理由.

(2)設A1(x1,y1),A2(x2,y2),A3(x3,y3),則

整理,得x-(y1+y2)y+y1y2=0.
同理可得直線A2A3的方程為
x-(y2+y3)y+y2y3=0.
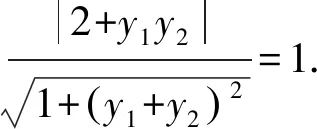
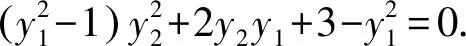
同理,由A1A3與⊙M相切可得
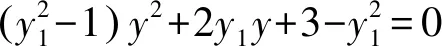
點M(2,0)到直線A2A3的距離為
所以直線A2A3與⊙M相切.
應用2已知拋物線y2=2px上三點A(2,2),B,C,直線AB,AC是圓(x-2)2+y2=1的兩條切線,則直線BC的方程為____.
解析易得拋物線方程為y2=2x.設A(x1,y1),B(x2,y2),C(x3,y3),其中x1=y1=2.

故直線BC的方程為3x+6y+4=0.
彭賽列閉合定理涉及圓錐曲線的兩條切線,故其本質上是處理圓錐曲線的雙切線問題.此類題型的運算量較大,考查了數學運算和邏輯推理等核心素養.破解此類題型的關鍵是靈活運用同構思想和韋達定理[1].

