數形結合顯“真功”
——妙解兩條曲線存在公切線
徐明松
(貴州省黔南布依族苗族自治州都勻第一中學,貴州 都勻 558000)
中國著名數學家華羅庚老師曾說:“數形結合本是相倚依,焉能分作兩邊飛?數缺形時少直觀,形少數時難入微;數形結合百般好,隔離分家萬事休;切莫忘,幾何代數統一體,永遠聯系,切莫分離”[1].在數學學習中,空間形式和數量關系是兩個最基本,也是最重要的研究對象.它們之間有著密切的關系,在一定條件下,可以相互轉化,相互滲透.
1 問題呈現,解法對比
題目若二次函數f(x)=x2+1的圖象與曲線C:g(x)=aex+1(a>0)存在公共切線,則實數a的取值范圍為____.
方法1 構造函數和方程,將公切線問題轉化為方程有根來解決.
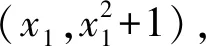
所以2x2=x1+2或x1=0.
又因為2x1=aex2>0, 所以x1>0.
所以2x2=x1+2>2.所以x2>1.
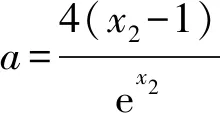
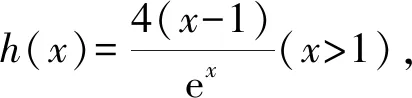
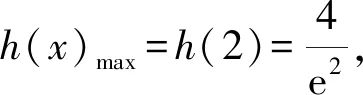
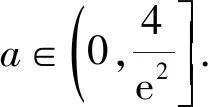
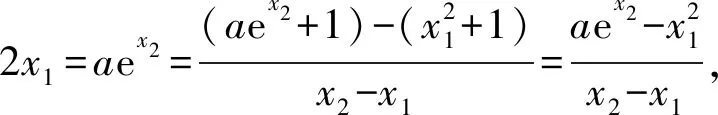
方法2 數形結合,直觀感知.
分析由于a>0,可先令a=1畫出題干中兩個函數的圖象(如圖1).
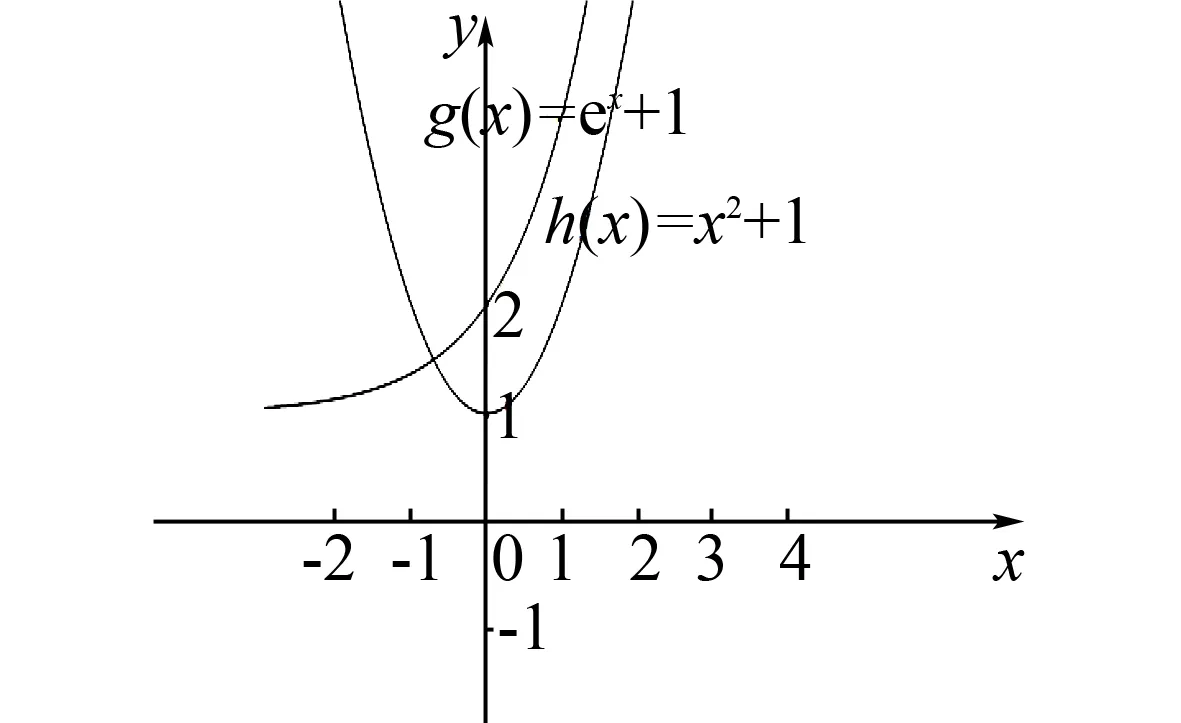
圖1 方法2示意圖
通過對圖象的直觀分析,要使兩個函數存在公切線,則公切線只能在第一象限,且兩個函數在x>0 部分的圖象至少有一個交點,當兩個函數在第一象限恰好相切時(如圖2),此時存在一條公切線,設切點為(x0,y0),則f′(x0)=2x0=g′(x0)=aex0.
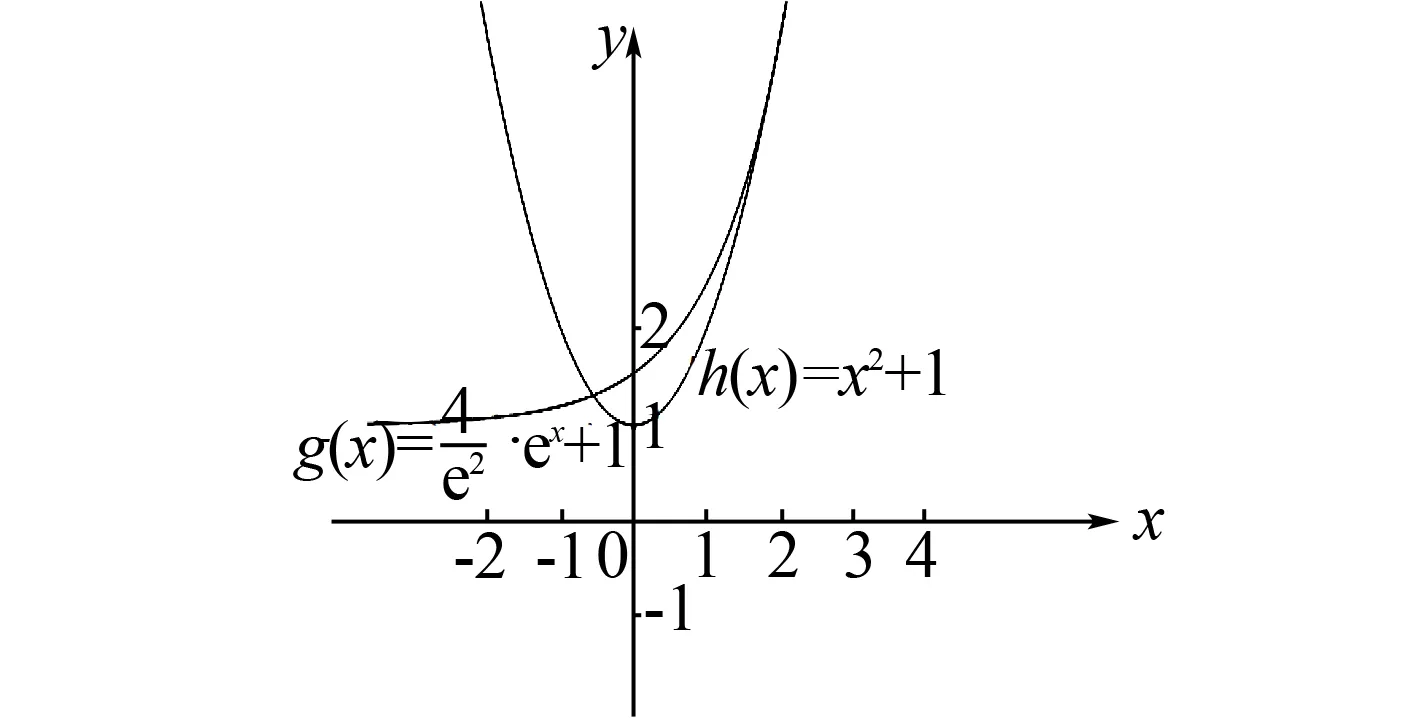
圖2 方法2示意圖
又f(x0)=g(x0),解得x0=2,y0=5.
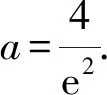
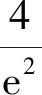
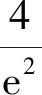
2 探究應用,彰顯數形結合
根據上面兩種方法對題目的處理,明顯用數形結合要直觀且易懂,下面舉兩個相應題目體現數形結合解決此類問題的優越性.
應用1已知曲線y=ex+a與y=(x-1)2恰好存在兩條公切線,則實數a的取值范圍為____.
分析此題如果采用上面方法1構造方程將非常困難,而且對化簡要求特別高,很難做出結果.下面直接采用數形結合的方法解決問題.函數y=ex+a中a的值影響函數左右平移情況,不訪先設a=0(如圖3).
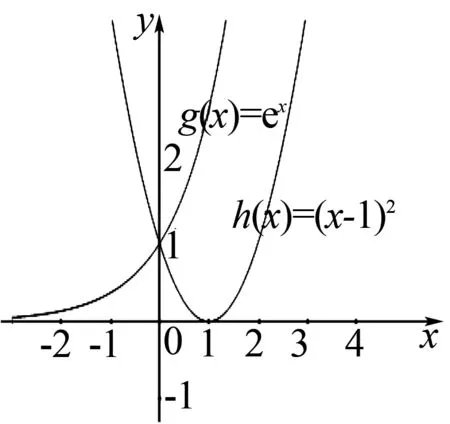
圖3 a=0時函數圖象
要使兩個函數存在公切線,只需將y=ex的圖象向右移,臨界在兩個圖象剛好相切(如圖4).
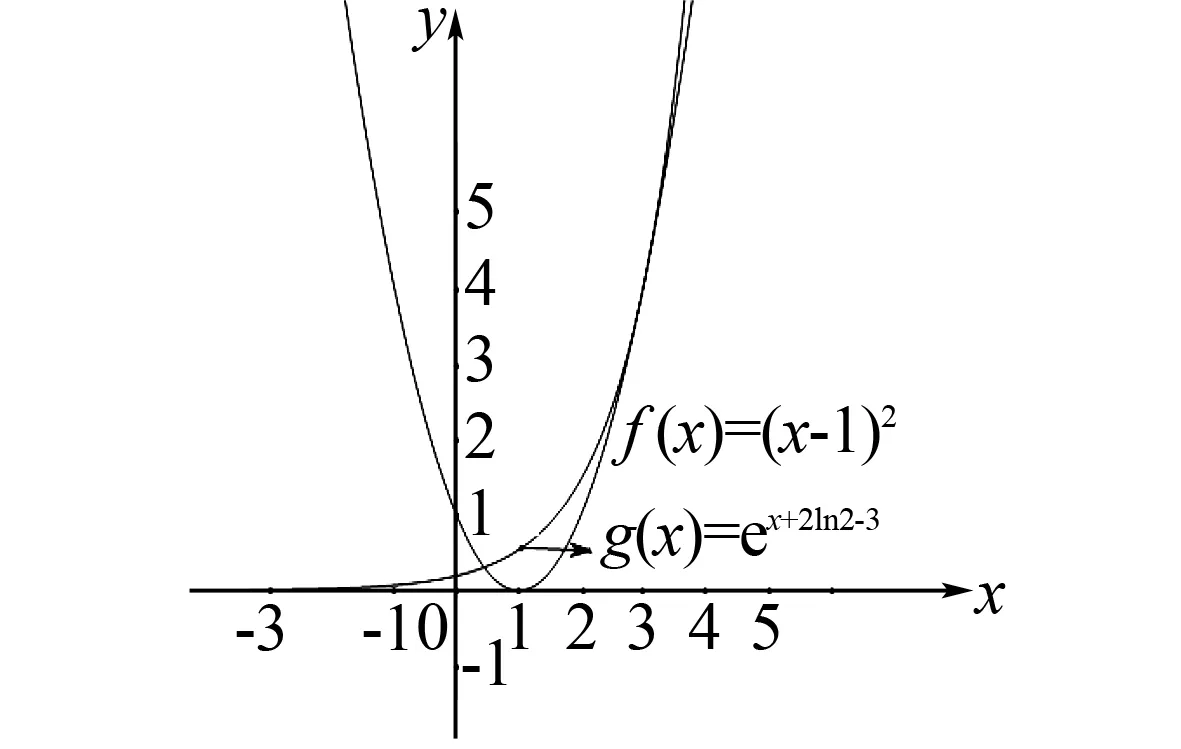
圖4 兩個函數臨界相切圖
設切點為(x0,y0),則ex0+a=2(x0-1),且ex0+a=(x0-1)2,整理,得a=2ln2-3,此時只存在一條公切線,要保證兩條公切線圖象需再右移,此時a<2ln2-3.
應用2若函數f(x)=lnx與函數g(x)=x2+2x+a(x<0)有公切線,則實數a的取值范圍是____.
分析直接采用數形結合解決問題.作出函數g(x)的變化圖(如圖5).
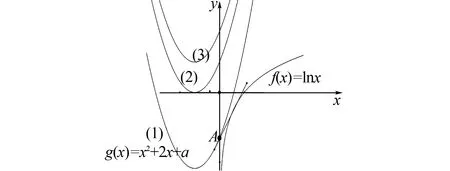
圖5 函數g(x)的變化圖
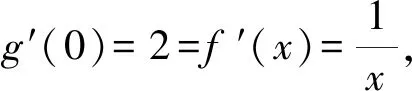
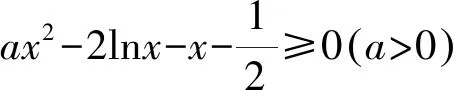
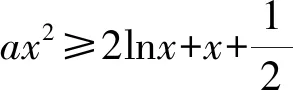
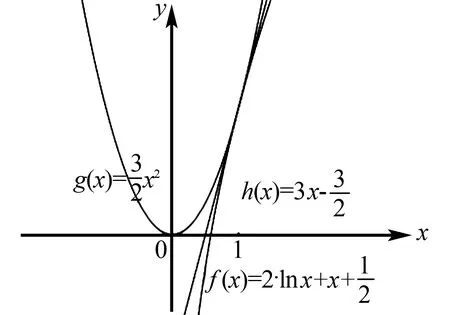
圖6 函數g(x),f(x)草圖象
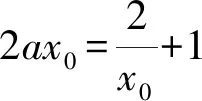
此題雖然不是直接考查兩曲線存在公切線,但可以轉化為兩曲線存在公切線時問題成立的臨界,然后通過圖象和計算可很快獲得實數a的范圍.
通過兩種不同方法的對比分析,解決兩曲線存在公切線求參數范圍時明顯看到數形結合的優勢,因此,教師在教學中必須注重學生數學思維能力的培養,注重數學思想方法的滲透和掌握,從而真正提高學生的數學思維和解題能力[2].對于函數問題多研究函數圖象,掌握好數形結合思想,以提高學生的直觀想象素養.

