借助開放式題型提高初中生數學解題能力

劉志娟 （江蘇省如東縣馬塘鎮邱陞中學）

當前初中生主要通過做題提高解題能力，除了做題，學生其他方面的體驗比較少。就做題而言，學生往往做的是答案唯一的題目。基于以上兩點原因，要想進一步提高學生的解題能力就需要教師豐富學生的體驗，同時還需要增加一些開放式題型。開放式題型往往因為設置的靈活性和思考的多維性更能促進學生思維的發展，也更能考查學生的解題能力。因此，教師要多設置開放式題型鍛煉學生的解題能力。

一、設置問題不固定題目

對于數學學習來說，學生不僅要學會解決問題，還要學會發現問題。當前的數學教學大多時候是教師呈現問題，學生解決問題。在這樣的教學模式下，學生發現問題的能力會減弱，不利于解題能力的提高。因此，在設置題目時，教師可以先設置一個情境，讓學生根據情境自己設置不同的問題。

問題情境：如圖1，學校統計學生早晨到校情況，從7：00開始校門口的學生人數y（單位：人）隨時間x（單位：分）變化情況的圖象是二次函數的一部分。

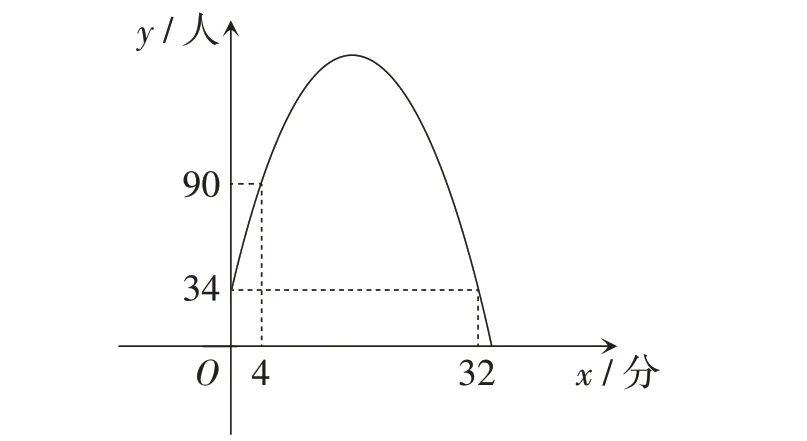
圖1

教師先讓學生對照函數圖象和情境內容提出問題。學生首先想到的是求y與x之間的函數解析式。對此，先設y與x之間的函數解析式為y=ax2+bx+c，對照圖象中給出的數據列出方程組，得解得所以教師鼓勵學生繼續提出問題，同時引導學生將題目的表述與圖象結合起來。看到圖象中變化的曲線，學生提出這樣的問題：“從7：00 開始，學生在什么時間能全部進入學校？”提出問題之后，學生在合作中轉化問題，發現問題的本質是求函數圖象與x軸的交點。令y=0，即解得x1=-2（舍），x2=34。所以學生在7：34時全部進入校園。

從整個解題過程來看，學生要先提高讀圖能力，能將題干中的表述與所給圖象對應起來。同時，學生還要提高借助圖象發現問題的能力，主動建構學習。設置問題不固定的開放式題型，能使學生根據自己的認知情況和學習能力提出與自己數學學習水平相當的問題。教師從學生的提問中可以發現他們的思維特點，進而進行針對性引導，促進學生解題能力的提高。學生自己提問，不僅增強了他們學習的主動性，還增強了解題的趣味性，使他們更愿意參與其中。

二、設置結論不固定題目

教師可以設置一些結論不固定的題目，以增加學生探究的機會。所謂結論不固定，就是教師只呈現題目的條件，進而讓學生依據條件推理出可能存在的結論。結論不固定題目可以給予學生更多思考的空間，也能提高他們的解題能力。教師要引導學生不僅要從條件出發，推斷出可能出現的結論，還要從結論出發進行逆向論證，以驗證條件是否充分利用。

題目1如圖2，將平行四邊形ABCD沿一條直線折疊，使點A與點C重合，點D落在點G處，折痕為EF，你能發現哪些結論？

圖2

學生先直觀感知題目，接著拿出一張紙剪成平行四邊形，進而標出對應的字母，再按照題目要求折疊。在折疊的過程中，他們相繼發現∠A=∠BCD，∠A=∠ECG， ∠ECB=∠FCG。觀察的過程其實就是學生解題的過程，觀察能力是重要的解題能力。觀察得出結論后，便開始證明。學生先由四邊形ABCD是平行四邊形得到∠A=∠BCD。再根據折疊的性質得到∠A=∠ECG，最后由∠BCD-∠ECF=∠ECG- ∠ECF，得∠ECB=∠FCG。教師追問：“是否有新的發現？”學生在折疊的過程中除了發現相等的角，還發現了一些相等的邊，由此他們猜想能不能找到全等三角形。基于發現的相等的角和相等的邊，學生發現△EBC≌△FGC，接著開始證明。學生由四邊形ABCD是平行四邊形，得∠D=∠B，AD=BC。再由折疊的性質，得∠G=∠D，CG=AD，所以∠B=∠G，BC=CG。因為∠ECB=∠FCG，所以△EBC≌△FGC()ASA。學生對照題目給出的條件，在操作、觀察中運用平行四邊形的性質、折疊的性質、全等三角形的判定等知識，完成了對結論的猜測與證明，提高了自己的解題能力。

三、設置解法不固定題目

開放式題型能激發學生的思維火花，讓學生更多地關注解題過程，而不再是一味地強調解題結果。解法不固定也是開放式題型的一種，即學生可以采用多樣的方式解決問題。教師可以鼓勵學生從不同的維度思考問題，拓寬解題思路的同時提高解題能力。

題目2如圖3，直線y=kx+ 8 與拋物線相交于兩點。

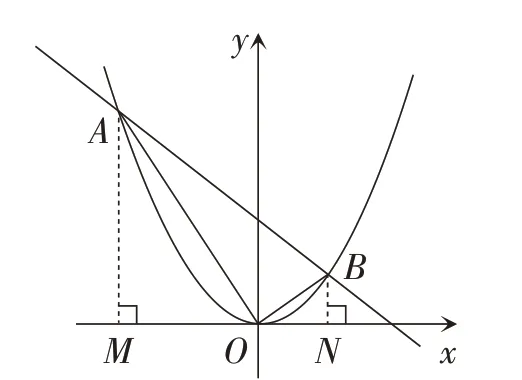
圖3

求證：（1）點(y1，y2)在反比例函數的圖象上；

（2）x1OB+y2OA=0。

對于第（1）小題，學生根據題意得出x2-8kx-64=0，進而得出x1x2= -64。因為所以可見點(y1，y2)在反比例函數的圖象上。對于第（2）小題，學生先想到了運用勾股定理直接表示OA，OB的長。由題意，知再由第（1）小題的結論得進而推出又因為x1＜0，y2＞0，所以-x1OB=y2OA，即x1OB+y2OA=0。完成證明后，學生想能不能將要證明的式子變形，寫成比的形式，再根據OA，OB為線段，將x1，y2與線段長度聯系起來。于是，學生過點A分別作AM⊥Ox，BN⊥Ox，垂足分別為點M，N。同樣地，利用第（1）小題的結論，由-x1x2=y1y2=64 得出OM·ON=AM·BN，即又因為∠AMO=∠ONB=90°，所以△AMO∽△ONB，進而推斷出即OM·OB=BN·OA。將這個等式化簡，得-x1OB=y2OA，即x1OB+y2OA=0。當完成第二種解法后，學生在想：有沒有第三種解法呢？他們運用解析式法，結合第（1）小題，由得出OA⊥OB，從而得到進而也得出從而得出最后的結果x1OB+y2OA=0。因此，教師要鼓勵學生多想一想有沒有更多的解法，要盡可能地創設解法多樣的題目，激活學生的思維，提高解題能力。

綜上所述，開放式題型能給學生提供更多思考的空間。教師可以依據學生的實際情況創設一些開放式題型，擴大學生思考的范圍和思維的深度，促使學生養成深度思考的習慣，進而提高解題能力。