基于局部化帶全局追蹤的露天煤礦邊坡臨界滑面確定方法研究

樊玉超

(國家能源集團新疆能源有限責任公司，新疆維吾爾自治區烏魯木齊市，830000)

0 引言

確定邊坡臨界滑面的位置是露天煤礦邊坡穩定性分析的關鍵問題，目前工程中常用的方法主要分為極限平衡法和有限元法兩類。極限平衡法一般采用滑面形狀為弧形或者多段型的假設，對整個露天煤礦邊坡區域進行遍歷搜索，計算各個假設滑面上塊體的靜力平衡方程，遴選出安全系數最小的滑面即為該邊坡的臨界滑面[1-3]。有限元法采用彈塑性本構模型計算露天煤礦邊坡的應力場和位移場，通過強度折減、過載等方式使邊坡達到臨界狀態，對有限元計算結果進行后處理，估算出滑面的位置。

目前，用于判斷露天煤礦邊坡失穩破壞的判據主要有3種：數值解非收斂判據[4]，以靜力平衡計算不收斂作為邊坡整體失穩的標志；塑性區貫通判據[5]，以塑性區或某一幅值的等效塑性應變由坡腳至坡頂貫通作為邊坡整體失穩的標志；位移突變判據[6]，以土體內某些點的應變和位移發生突變且無限發展作為邊坡整體失穩的標志。

確定臨界滑動面空間位置的方法包括：基于畸變網格或貫通的塑性應變等色圖[4，7]；沿深度方向搜索最大塑性應變、最大剪應變增量、最大位移變化率位置[8-10]；求解滑動面控制方程[11-12]；對邊坡位移及節點安全系數聚類[13]。

與極限平衡法相比，有限元法考慮巖土體變形協調條件與本構關系，可以模擬露天煤礦邊坡漸進破壞過程，能夠更好地適用于各種復雜工況條件。然而，有限元法中邊坡失穩狀態的判識與臨界滑面的確定通常互相割裂，彼此之間缺乏內在關聯。為此，提出一種局部追蹤算法[14]，通過追蹤局部化帶形成、擴展、匯合直至貫通的過程，在判斷邊坡的極限平衡狀態的同時，確定臨界滑動面的位置。局部追蹤算法在處理單條局部化帶擴展時十分簡單，但在處理多條局部化帶擴展時非常繁雜，缺少魯棒性，并且構造的局部化帶路徑也不光滑。

為解決上述問題，引入OLIVER J等[15-16]提出的全局追蹤算法(Global Tracking Algorithm)，結合局部化帶貫通判據，發展一種基于全局追蹤算法的露天煤礦邊坡臨界滑面確定方法，并通過算例分析驗證了臨界滑面確定方法的有效性。

1 材料失效理論與邊坡失穩判據

1.1 材料失效理論

局部化帶理論[17-18]認為，土體材料失效表現為由原先光滑、連續化的變形模式轉變為以劇烈變形狹窄條帶形式出現的、高度局部化的變形模式。如圖1所示，當土體材料出現劇烈變形的局部化帶時，位移率在跨越局部化帶時保持連續，而位移梯度率出現間斷，即：

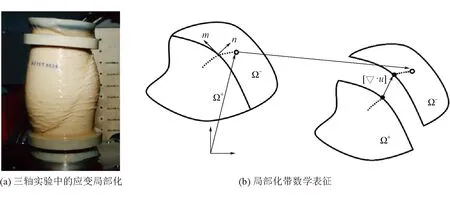
圖1 土體材料應變局部化現象

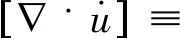
(1)

“+”“-”——帶狀區域的正表面和負表面；

n——局部化帶的單位法向量；

m——局部化帶的單位切向量；

1.2 邊坡失穩判據

在局部化帶理論框架下，邊坡失穩破壞過程可以看作土體單元不斷發生局部化失效的過程。坡體內部局部化帶演化如圖2所示。

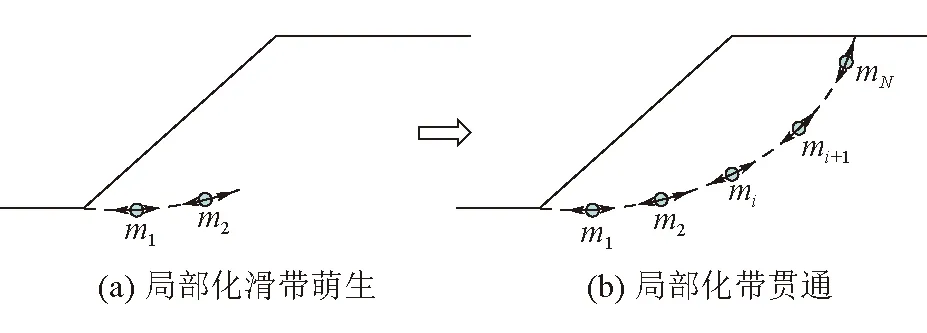
圖2 坡體內部局部化帶演化

由于邊坡內材料的非均勻性、初始弱面的存在以及非均勻分布的荷載與邊界約束，邊坡內部的應力場始終是不均勻的，一些應力集中單元率先發生實現，形成局部化帶。隨著外部荷載的增加、材料強度的減小以及土體單元實現后釋放載荷在邊坡內部的轉移和調整，新的局部化帶不斷形成，已有的局部化帶繼續擴展、匯合，直至在坡體內部完全貫通。在此極限狀態，處于局部化的土體單元沿其局部化帶滑移方向除承擔與其強度相適應的載荷之外，已無能力承擔附加荷載，任何微小的擾動都可能導致滑體沿連續貫通的局部化帶發生大變形，最終引發邊坡模型的整體失穩。

因此，可將局部化帶由坡底至坡頂的完全連續貫通時刻定義為邊坡力學模型的極限平衡狀態，將局部化帶的貫通路徑定義為邊坡模型的臨界滑動面。只要準確地追蹤到局部化帶自萌生至貫通的完整路徑，即可同時確定邊坡模型的極限狀態和滑動面位置。

2 局部化帶追蹤技術

2.1 局部化信息

為準確追蹤局部化帶路徑、確定邊坡臨界滑面，需要發展有效的追蹤技術，即根據每個時間步邊坡有限元計算結果，通過局部化帶追蹤算法，以后處理的方式再現邊坡內部局部化帶的演化狀態與擴展路徑。在局部化帶理論框架下，從邊坡有限元計算結果中提取追蹤算法所需的兩類信息。

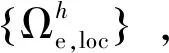
(2)

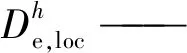
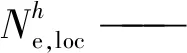
(3)

考慮到滿足式(2)的解不唯一，當有限元單元發生局部化失穩時，至少存在2組潛在的局部化擴展方向。本篇采用“沿實際局部化帶切線方向，絕對位移率分量最大”原則，從多個候選局部化向量中選取局部化帶的實際擴展方向，其數學表達式為：

(4)

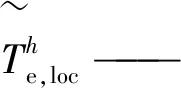
2.2 追蹤算法

在數值實現時，邊坡有限元將整個邊坡離散為一組單元的組合體，將連續的無限自由度問題變成離散的有限自由度問題。由于單元內部的應力場被平均化處理，由單元積分點(高斯點)的應力近似代表，因此對于滿足式(2)的局部化單元，局部化帶出現的位置是不確定的，可以出現在局部化單元的任意區域。

為此，發展了局部追蹤算法(Local Tracking Algorithms)和全局追蹤算法(Global Tracking Algorithms)來確定局部化帶的具體擴展路徑。這兩類算法均遵循如下假定條件：局部化帶以離散線段形式在每個局部化單元中擴展；局部化帶在相鄰單元擴展時，要求保持連續性。

2.2.1 局部追蹤算法

根據前文給出的局部化信息，局部追蹤算法從根單元出發，逐個單元地追蹤局部化帶擴展路徑。局部追蹤算法示意如圖3所示。

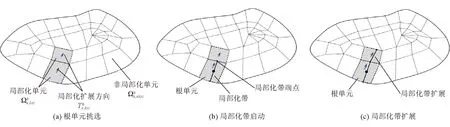
圖3 局部追蹤算法示意

局部追蹤算法基本流程如下所示。

(1)根單元挑選。從局部化單元集合中挑選出最早進入局部化的單元，將其定義為根單元，如圖3(a)所示。

(2)局部化帶啟動。從根單元的中心點出發，局部化帶沿局部化擴展方向擴展至單元邊界，如圖3(b)所示。

(3)局部化帶擴展。核查局部化帶端點兩側單元是否為局部化單元，如果是，從局部化帶端點出發，繼續沿對應單元的局部化擴展方向擴展局部化帶，直至到達邊界或局部化帶端點兩側單元為非局部化單元，如圖3(c)所示。

局部追蹤算法在處理單條局部化帶擴展時十分簡單，但在處理多條局部化帶擴展時非常繁雜[14-16]，缺少魯棒性，并且構造的局部化帶路徑也不光滑。

2.2.2 全局追蹤算法

全局追蹤算法將局部化帶路徑追蹤問題轉換為求解穩態熱傳導類問題，由等溫線獲得所有潛在局部化帶，從中確定局部化帶擴展路徑，如圖4所示。

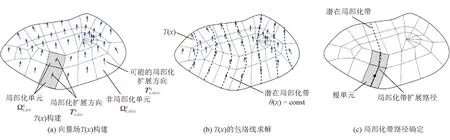
圖4 全局追蹤算法示意

全局追蹤算法分為3個部分：

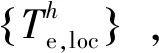
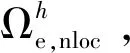
(5)

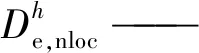
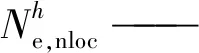
(2)求解向量場T(x)的包絡線(潛在局部化帶)。邊坡內部的局部化帶可以看作無厚度的曲線集合{Si}，曲線Si上任意坐標x處的切線方向為局部化擴展方向T(x)。因此，從數學角度看，追蹤局部化帶路徑等同于求解向量場T(x)的包絡線。

在邊坡區域Ω內定義標量函數θ(x)，使其梯度與T(x)始終正交，即：

T(x)·?θ(x)=0x∈Ω

(6)

考慮到函數θ(x)的等值線(θ(x)為常數)垂直于梯度?θ(x)，可知θ(x)的等值線即為向量場T(x)的包絡線，物理上代表所有潛在局部化帶，如圖4(b)所示。

為了求解θ(x)，在式(6)等號兩邊同乘T(x)，將式(6)擴展為一組熱傳導類偏微分方程組，即：

(7)

式中：υ——垂直于?qΩ的單位向量；

θd——在Dirichlet邊界條件上的值。

為獲得θ(x)的非零解，應至少對位于不同等值線上的2個節點設置θd。并且，考慮到K(x)存在奇異性，需要將式(7)中的K(x)=T(x)?T(x)修正為：

K(x)=T(x)?T(x)+∈I

(8)

式中：I——單位張量；

∈——數值很小的各項同性熱導率。

式(7)表明，標量函數θ(x)可以類比為溫度場，-(K(x)?θ(x))為熱通量，K(x)為各向異性熱傳導張量。因此，追蹤局部化帶路徑問題轉變為求解無內部熱源和零熱通量輸入的穩態熱傳導類問題，通過求解溫度場的等溫線，獲得所有潛在局部化帶。

(3)確定局部化帶擴展路徑。在獲得所有潛在局部化帶后，需要從中確定局部化帶擴展路徑。從未追蹤的局部化單元集合中挑選出最早進入局部化的單元(根單元)，將通過根單元中心點的等溫線標記為潛在局部化帶，如圖4(c)所示。追蹤與潛在局部化帶相交的所有局部化單元，將其標記為已追蹤局部化單元，將潛在局部化帶與這些局部化單元的相交線段標記為局部化帶擴展路徑。

如果局部化單元集合中仍然存在未被追蹤的局部化單元，則繼續從未追蹤的局部化單元中挑選下一個根單元，開始下一條局部化帶路徑追蹤，直至所有局部化單元均已追蹤完畢。

3 邊坡臨界滑面判識流程

與局部追蹤算法相比，全局追蹤算法理論推導嚴密，更適合于多局部化帶路徑追蹤問題。因此，可以基于全局追蹤算法來判識邊坡臨界滑面，具體實施流程如下。

(1)作為后處理程序，邊坡臨界滑面判識程序在每個或每幾個時間步結束后調用，通過追蹤當前荷載下局部化帶擴展路徑來判識邊坡滑面狀態。

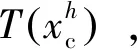
(6)核查局部化單元是否全部標記為已追蹤狀態。如果不是，轉步驟(5)，開始下一條局部化帶路徑追蹤。如果是，則完成全部局部化帶路徑追蹤。

(7)根據各條局部化帶路徑，判斷局部化帶貫通情況。如果某條局部化帶由坡底至坡頂完全連續貫通，則整個邊坡處于極限平衡狀態，該條局部化帶擴展路徑為臨界滑面，邊坡穩定性計算結束；如果沒有，則轉步驟(1)，開始下一個時間步長加載及邊坡穩定性計算。

4 有限元數值實現

全局追蹤算法的數值實現流程：使用邊坡有限元模型網格，將給定的邊坡區域Ω離散為nelem個有限單元和nnode個有限節點。采用有限元方法將穩態熱傳導控制方程(7)離散化[19]，導出其對應的離散形式，即：

尋找：

以致：

(10)

式中：Ni(x)——標準形函數；

K——相應的剛度矩陣。

作為后處理程序，式(10)需要在邊坡穩定性計算的每個或每幾個時間步完成后調用，并且根據前文描述的追蹤算法判識邊坡臨界滑面來確定每個局部化單元中局部化帶的具體擴展位置，見步驟(4)～(7)。

需要注意的是，如果未指定邊界溫度(?θΩ=???qΩ=?Ω)，則K矩陣的秩為nnode-1。因此，必須在至少一個節點處指定溫度，以確保有限元方程(10)具有唯一解。此外，為了避免溫度場θ出現常數解(這將無法區分不同的等溫線)，應在另一個節點處指定溫度。如何指定溫度值不影響局部化帶位置的判定，只要不在同一條等溫線上的2個點上施加2種不同的溫度值即可。

5 算例驗證

為驗證全局追蹤算法的有效性，分別采用強度折減和位移加載方式，開展兩類邊坡臨界滑面追蹤數值分析。土體材料均為理想彈塑性材料，屈服準則為平面應變條件下摩爾-庫侖結合DP準則(DP4準則)。

5.1 算例1：強度折減

采用文獻[4，14]中的邊坡算例：邊坡坡高H=20 m，坡角β=26.57°，楊氏模量E=100 MPa，泊松比v=0.3，容重γ=20 kN/m3，黏聚力c=10 kPa，內摩擦角φ=20°。土體材料為理想彈塑性材料，強度準則采用平面應變條件下摩爾-庫侖結合DP準則(DP4準則)。算例1邊坡尺寸及網格劃分如圖5所示，邊坡左、右兩側邊界為法向約束，底邊為雙向固定約束，共劃分四邊形單元5 686個、節點5 878個。采用有限元強度折減方法，按照c/ω，tanφ/ω方式不斷折減土體材料強度參數，模擬邊坡漸進破壞過程及其位移場演化信息，直至邊坡發生整體失穩。其中，ω為折減系數，其初始值ω0=1.0，步長△ω=0.002。

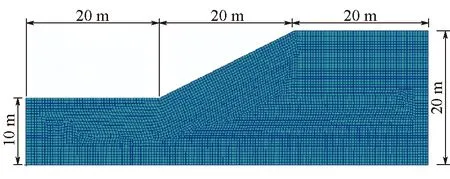
圖5 算例1邊坡尺寸及網格劃分

折減系數ω=1.384時等效塑性應變云圖如圖6所示。由圖6可以大致確定滑動面的分布范圍，但無法精確定位。

圖6 折減系數ω=1.384時等效塑性應變云圖

采用文獻[12]中局部追蹤技術，折減系數ω=1.384時局部化帶擴展路徑如圖7所示[12]。由圖7可以看出，局部追蹤技術給出的局部化區域要比塑性云圖的范圍小得多，主要集中在邊坡的局部破壞區域。然而在坡角及坡肩附近，多條局部化帶相互交織，并不光滑，這給臨界局部化帶位置的判識帶來了困難。此外，這些局部化滑帶寬度與有限元網格尺寸相關，通常占據2～3個單元。

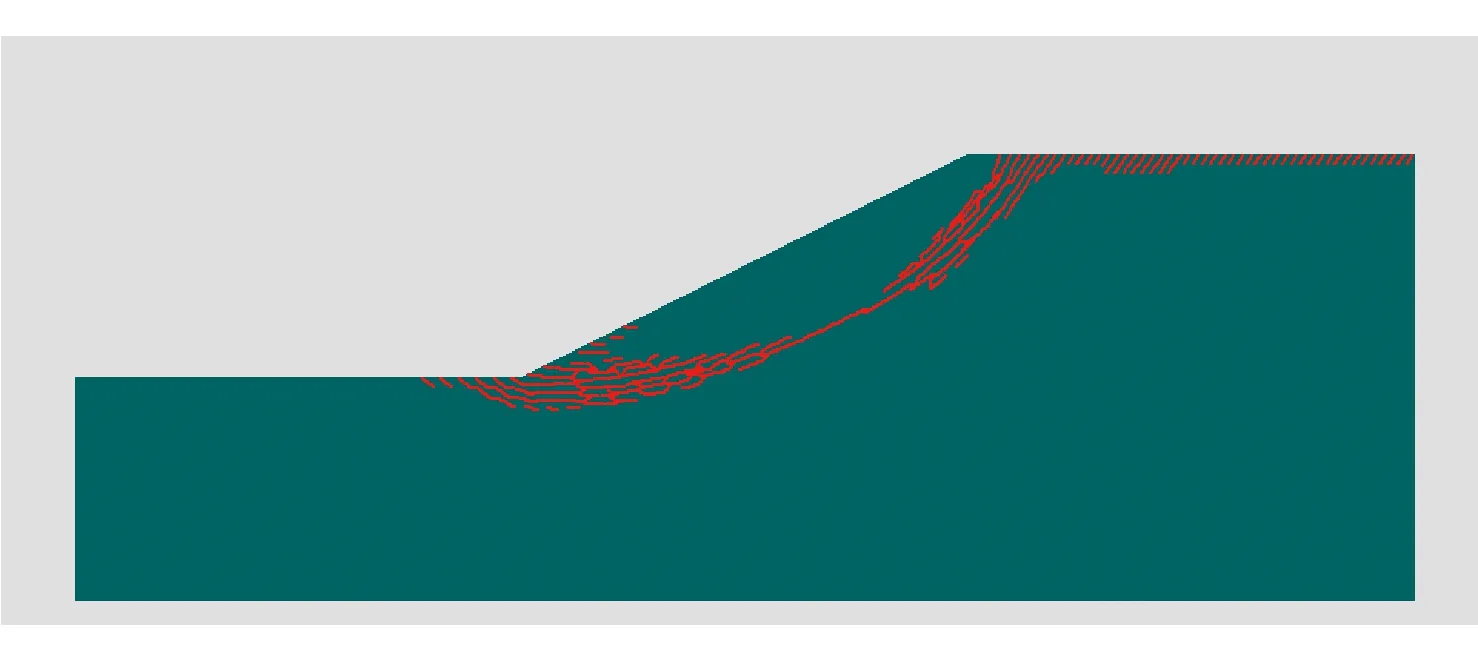
圖7 折減系數ω=1.384時局部化帶擴展路徑

折減系數ω=1.384時，采用全局追蹤技術獲得的溫度場等值線和局部化帶擴展路徑如圖8所示。與局部追蹤技術相比，全局追蹤技術同時利用局部化單元的擴展方向和非局部化單元可能的擴展方向求解邊坡向量場的包絡線，從而從所有潛在局部化帶中確定局部化帶擴展路徑。這種方法追蹤滑面的魯棒性更高，不僅主級滑面(紅色線條)為無厚度的光滑曲線，次級滑面(藍色線條)清晰，而且各級滑面之間以層狀方式平行分布，不再出現滑面彼此交叉的情況。

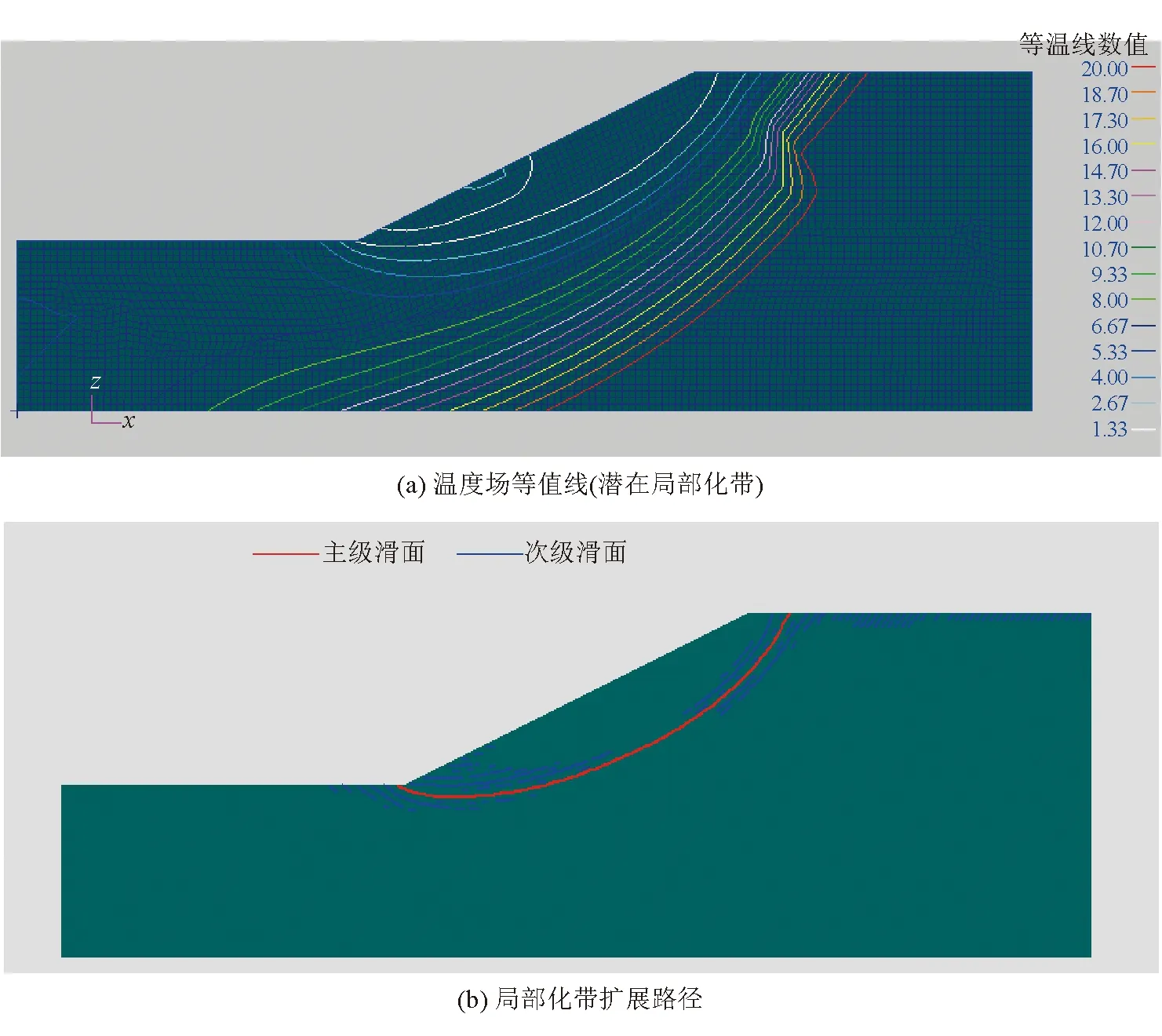
圖8 折減系數ω=1.384時采用全局追蹤技術追蹤效果

通過以上對比可以看出，借助塑性應變云圖的傳統臨界滑動面確定方法具有很大的局限性，僅能大致確定滑動面的分布范圍；局部追蹤技術雖然能夠給出更具體的局部化區域，但在坡角及坡肩附近的局部化帶相互交織，影響了臨界局部化帶位置的判識；而全局追蹤技術則能夠克服這些問題，提供更準確、更全面的局部化帶擴展路徑信息。

5.2 算例2：位移加載

采用文獻[14，20]中的邊坡算例：坡高H=10 m，坡角β= 45°，楊氏模量E= 10 MPa，泊松比v= 0.4，容重γ= 20 kN/m3，黏聚力c= 20 kPa，內摩擦角φ= 30°。邊坡幾何尺寸及網格劃分如圖9所示，邊坡右側邊界為法向約束，底邊為雙向固定約束。除重力載荷G外，邊坡在坡頂承受豎直向下位移u作用，F為豎向位移u產生的豎向反力。重力載荷通過初始應力場體現，所產生的位移不計入豎向位移u中。

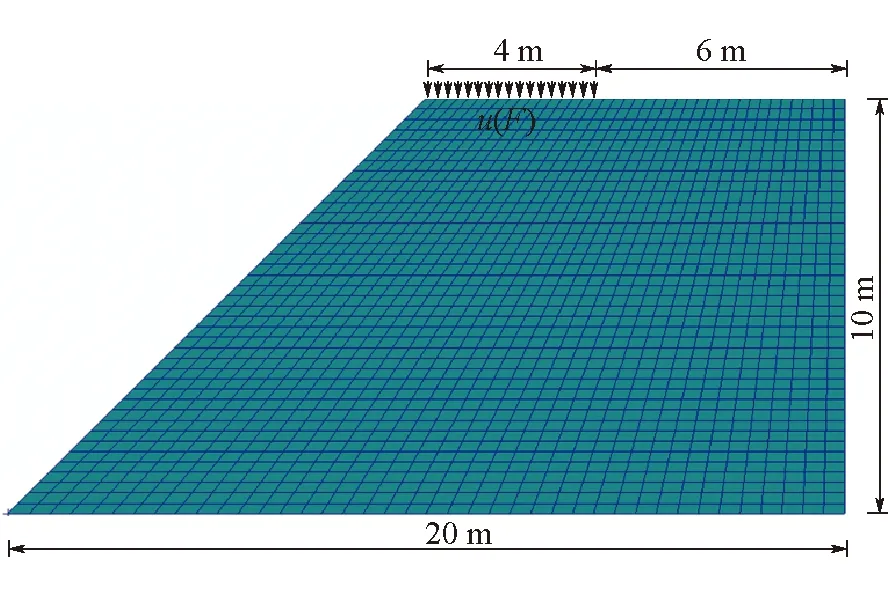
圖9 算例2邊坡幾何尺寸及網格劃分

邊坡在失穩臨界狀態下(豎向位移u=0.14 m)的等效塑性應變云圖、采用局部追蹤技術和全局追蹤技術獲得的局部化帶擴展路徑如圖10～12所示。由圖10～12可以看出：通過塑性應變云圖呈現出2條條帶狀分布的貫通滑動面，無法準確判斷臨界滑動面的位置；局部追蹤技術和全局追蹤技術都能夠判斷臨界滑動面的位置；然而，局部追蹤技術給出的臨界滑面不夠準確，其路徑不光滑，且在坡體下半區域內的局部滑帶也呈現出條帶狀分布，占據了2～3個單元的厚度；與局部追蹤技術相比，全局追蹤技術追蹤的主級滑面(紅色線條)以無厚度的光滑曲線的方式呈現，沒有出現滑面互相交叉以及滑面條帶化的情況，因此，全局追蹤技術可以為后續的邊坡工程治理提供更有效地支撐。

圖11 u=0.14 m時局部化帶擴展路徑

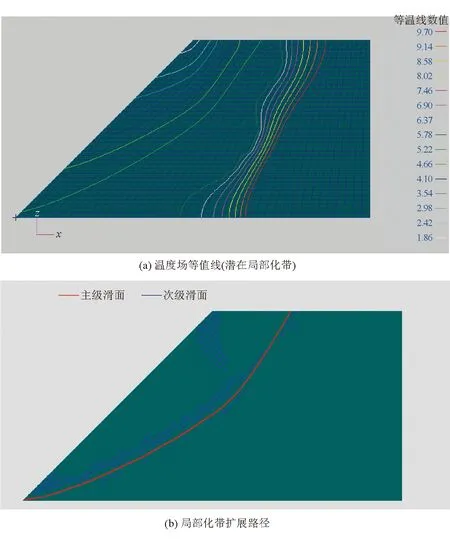
圖12 u=0.14 m時采用全局追蹤技術追蹤效果

通過對比分析，可以得出全局追蹤技術在追蹤邊坡滑動面方面具有更高的魯棒性和準確性，能夠以光滑曲線的方式呈現局部化帶路徑，克服了傳統方法和局部追蹤技術的局限性，從而為后續的邊坡工程治理提供了重要的分析支撐手段。

6 結論

(1)在局部化帶理論框架下，將全局追蹤算法與局部化帶貫通判據相結合，提出了一種基于全局追蹤技術的露天煤礦邊坡臨界滑面確定方法。該方法將追蹤局部化帶路徑的問題轉化為求解無內部熱源和零熱通量輸入的穩態熱傳導問題，通過追蹤經過局部化單元中心的等溫線來辨識局部化帶路徑的擴展及貫通狀況。

(2)算例結果比對分析表明：借助塑性應變云圖的傳統臨界滑動面確定方法存在很大的局限性，只能大致確定滑動面的分布范圍，而無法準確定位；局部追蹤技術雖然能夠給出更具體的局部化區域，但局部化帶經常相互交織，影響了臨界局部化帶位置的精準判識，此外，局部追蹤技術給出的臨界滑面不夠準確，其路徑不光滑，經常呈現出條帶狀分布特點；基于全局追蹤技術的邊坡臨界滑面確定方法具有更好的魯棒性，它能以光滑曲線的方式呈現滑面，不會出現滑面互相交叉以及滑面條帶化的情況。這種方法更適合多條局部化帶同時擴展情況下的臨界滑面的確定。

(3)提出的全局追蹤技術結合局部化帶貫通判據的方法能夠有效地確定邊坡的臨界滑面，克服了傳統方法的局限性。