免標定壁面剪應力測量技術研究

劉 丹

（中國飛行試驗研究院，西安 710089）

根據牛頓黏性流體定律，剪應力與邊界層內速度梯度直接相關，有如下關系

式中：μ 為流體動黏性系數，u 為流速。

壁面剪應力傳感器的標定是其應用于試驗測量的基本前提，即建立能夠反映剪應力傳感器輸出信號（E）與給定的定常壁面剪應力之間內在關系的數學模型。也就是說，標定是測量的逆過程[1]

壁面剪應力傳感器的靜態標定需要施加穩定已知量值的剪應力，讀取對應輸出。采用流體力學經典模型，通過測量其他物理量從而換算得到對應壁面剪應力值是常用方法[2-3]。動態剪應力標定需要加載一個周期性變化的剪應力。通常動態標定是為了研究傳感器在中頻或者高頻激勵下的響應情況，因此需要動態標定裝置能產生較高頻率的激勵信號[4-5]。

壁面剪應力傳感器的標定方法有很多，它們并不統一，但都需要提供穩定可靠且量級相當的壁面剪應力用于標定，并且需要重復多次測量數據來分析壁面剪應力測量的不確定度及電壓信號測量的不確定度[6-8]。正是由于各類標定方法的復雜性，免標定方法已經成為一種新趨勢。

壁面剪應力傳感器的種類較多，常見的有浮動元件式傳感器、熱線/熱膜式傳感器和底層隔板等。其中，基于熱傳遞的熱膜傳感器體積小、應用快、發展快。具有對流場干擾小、空間分辨率和帶寬高、可靠性好等優點，應用較為廣泛[9-11]。熱膜式壁面剪應力傳感器主要基于對流換熱的原理，當電流加熱敏感單元產生的熱能在不同流動情況下通過對流散熱的形式轉移到流場中，引起熱敏電阻阻值的變化而表征出壁面剪應力[12-13]。

1 熱膜傳感器的原理

熱膜流速測量法基于壁面剪應力和從嵌入式等溫金屬膜到流體流動的對流傳熱速率之間的關系，首先由Lévêque、Wang 等[14-15]提出，其適用于具有線性速度剖面的流動。Ludwieg[16]將Lévêque 的分析擴展到湍流邊界層后，得出了類似的解

傳熱系數的精確測量并不簡單。熱膜產生的焦耳熱的很大一部分會通過壁面損失，而不是轉移到流體中，因此始終需要進行標定以確定和τw之間的關系。然而，其標定結果易受環境溫度變化的影響，因此該方法不可靠，除非在控制良好的環境中[17-18]。以前的大多數研究并沒有標定熱膜傳感器，只在定性觀測中對其進行了使用[19-20]。

使用熱膜傳感器進行可靠的定量測量需要消除通過基板的熱損失。被動隔熱方法，如熱膜傳感器下方的真空腔，由此而生[21]。然而，盡管其在靈敏度、帶寬和功耗方面有了改進，但熱損失仍然很大。之后研究人員又提出了一種使用與熱膜傳感器具有相同溫度的保護加熱器的主動隔熱方法，并通過數值模擬[22]證明了該方法的有效性。主動隔熱的想法很有吸引力，然而，傳感器和保護加熱器之間的溫差需要小于零點幾攝氏度，這對現有技術是一個挑戰。

Liu 等[23]首先成功地實現了主動隔熱。他們設計了一種雙層熱膜傳感器，如圖1 所示，由1 個非導電膜夾在2 層薄金屬膜之間組成。這2 層薄膜在相同的溫度下工作，下層薄膜作為上層薄膜的主動熱絕緣體。通過在2 個獨立的四線開爾文橋流速測量系統中使用高精度的電阻，它們能夠將2 層薄膜之間的溫差降低到0.14°C 以下[24]。使用不同的電流加熱薄膜來調節薄膜溫度，薄膜的電阻會隨著溫度的變化而變化。例如，上層薄膜溫度Tu與其電阻Ru有關

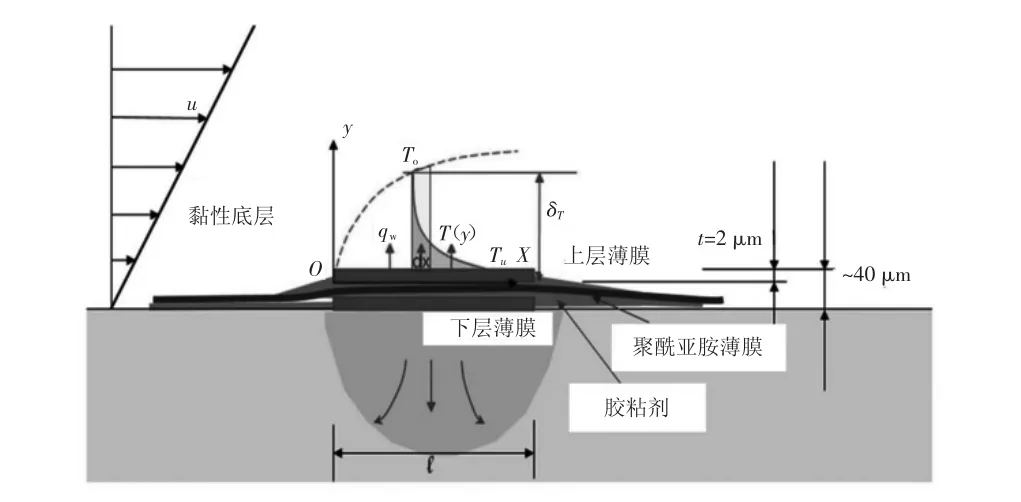
圖1 雙層熱膜傳感器示意圖

這里，Ruo是環境溫度中上層薄膜的電阻值。實際上，上層和下層薄膜連接在2 個獨立的開爾文橋中，其中一個如圖2 所示。通過手動修改每個電橋中R1和R22 個電位計的阻值來調整薄膜溫度。另外2 個電位計R3和R4的阻值分別設置為R1和R2。電橋達到平衡后的結果Ru為

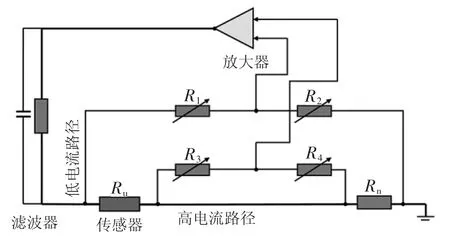
圖2 基于四線開爾文電橋的恒溫風速儀（CTA）示意圖

基于這一溫差原理，Liu 等[25]估計，上層薄膜產生的焦耳熱總量中，只有不到5%的熱量通過基板散失，其余的熱量都轉移到流體中，由此提出了免標定壁面剪應力測量方法的概念，該方法利用傳熱和動量傳遞之間的關系來測量上層薄膜的焦耳熱，然后根據式（3）計算得到壁面剪應力。

2 理論模型

2.1 方向性效應

傳熱速率不僅會隨應力的大小而變化，還隨應力的方向而變化。Sumer 等[26]研究了表面貼裝單層熱膜傳感器的方向效應。當熱膜傳感器的窄邊平行于τw的方向時，恒溫風速儀的原始電壓輸出最大，表明在這種情況下熱膜產生的焦耳熱最大。焦耳熱隨著偏航角（傳感器和應力之間的角度）的增加而降低。按照相同的方法[27]模擬從傾斜熱線傳感器到冷環境流體的傳熱，Elvery 等[28]通過實驗研究了橫流速度分量對傳熱速率的影響。與熱線傳感器相比，熱膜傳感器的傳熱對偏航角的變化更為敏感：靈敏度（偏航系數k1）要大一個數量級。

從上層薄膜轉移到流體的總熱通量為

式中：we=wcosα 和le=l/cosα 分別是有效寬度和有效長度，ΔT=TW-T0是薄膜和環境流體之間的溫度差。從式（7）中可以看出，平均努塞爾數為

方向效應和缺乏這種效應的精確模型阻礙了熱膜流速儀在大多數飛行器、航行器表面應力測量中的應用[29]。例如，氣流在鈍體（如飛機機翼）上分離，會產生復雜的非定常近壁流動模式。在這種情況下，單個壁掛式熱膜傳感器無法區分表面流動大小和方向的瞬態變化。Sumer 等[30]利用一對垂直定位的熱膜傳感器，開發出一種能夠測量應力矢量的雙組分壁面剪應力測量技術。然而，該技術需要精密耗時的標定過程，且標定結果容易受到環境溫度微小變化的影響[31]。

2.2 雙組分免標定測量技術

這里提出了一種無需標定即可測量局部壁面剪應力大小和方向的技術。該技術使用兩個尺寸相同的雙層熱膜傳感器，彼此靠近并垂直放置，形成V 形（圖3）。坐標x和z分別沿著和垂直于傳感器對的中心線。應力方向與傳感器對中心線之間存在任意角度β。因此，應力與2 個傳感器之間的角度分別為α1=β-π/4 和α2=β+π/4。從2 個傳感器傳遞到流體的熱量為

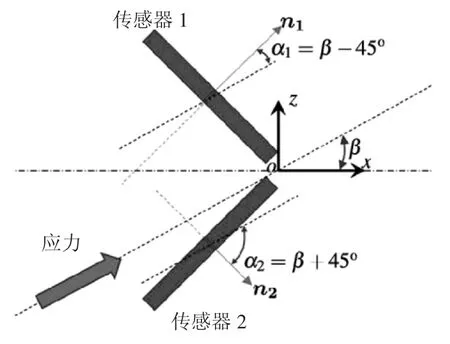
圖3 以V 形排布的雙組分傳感器示意圖

通過求解線性方程（9）和（10）可得到壁面剪應力的大小和方向，條件是2 個傳感器具有相同的尺寸和相同的工作溫度（A1=A2=A和ΔT1=ΔT2=ΔT）

在這項技術中，使用下一節討論的風速測量系統測量從2 個傳感器Q1和Q2傳遞到流體的熱通量。

3 驗證實驗

為了證明方向效應理論（式（6）或式（7）），并驗證雙組分免標定測量技術（式（11）和式（12）），Liu 等[24]設置了3 個獨立的驗證實驗。在實驗一中，雙膜傳感器中上層薄膜產生的壁面剪應力和焦耳熱之間的關系在長管設施中進行了標定。

在實驗二中，將標定后的雙膜傳感器安裝在風洞中浸入湍流邊界層的轉臺表面。通過旋轉轉臺，研究了方向效應對傳感器到流體傳熱的影響。在實驗三中，通過使用一對未標定的傳感器將所測得的壁面剪應力矢量與已知值進行比較，驗證了所提出技術的可行性。在所有實驗中，傳感器均由開爾文橋流速測量系統驅動。

3.1 實驗一：單個雙層傳感器的標定

在實驗一中，使用長管裝置研究了雙膜傳感器中上層薄膜產生的焦耳熱（Q）與傳感器位置處的局部壁面剪應力之間的關系，這是應力標定的標準方法[32]。該設施的示意圖如圖4 所示。

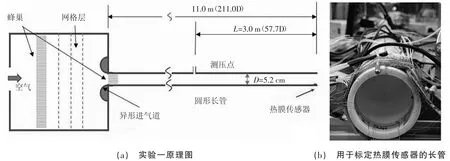
圖4 傳感器標定示意圖

3.2 實驗二：方向效應

經過標定的雙層熱膜傳感器，在閉式回流風洞中研究了其方向效應。風洞有一個0.3 m 寬、0.3 m 高、0.7 m 長的試驗段，如圖5（a）—（c）所示。將經過標定的熱膜傳感器置于壁面剪應力方向的法線上（α=0°），利用實驗一中獲得的標定結果測量局部壁面剪應力的大小和熱通量Q，并給出了每個偏航角的平均值。

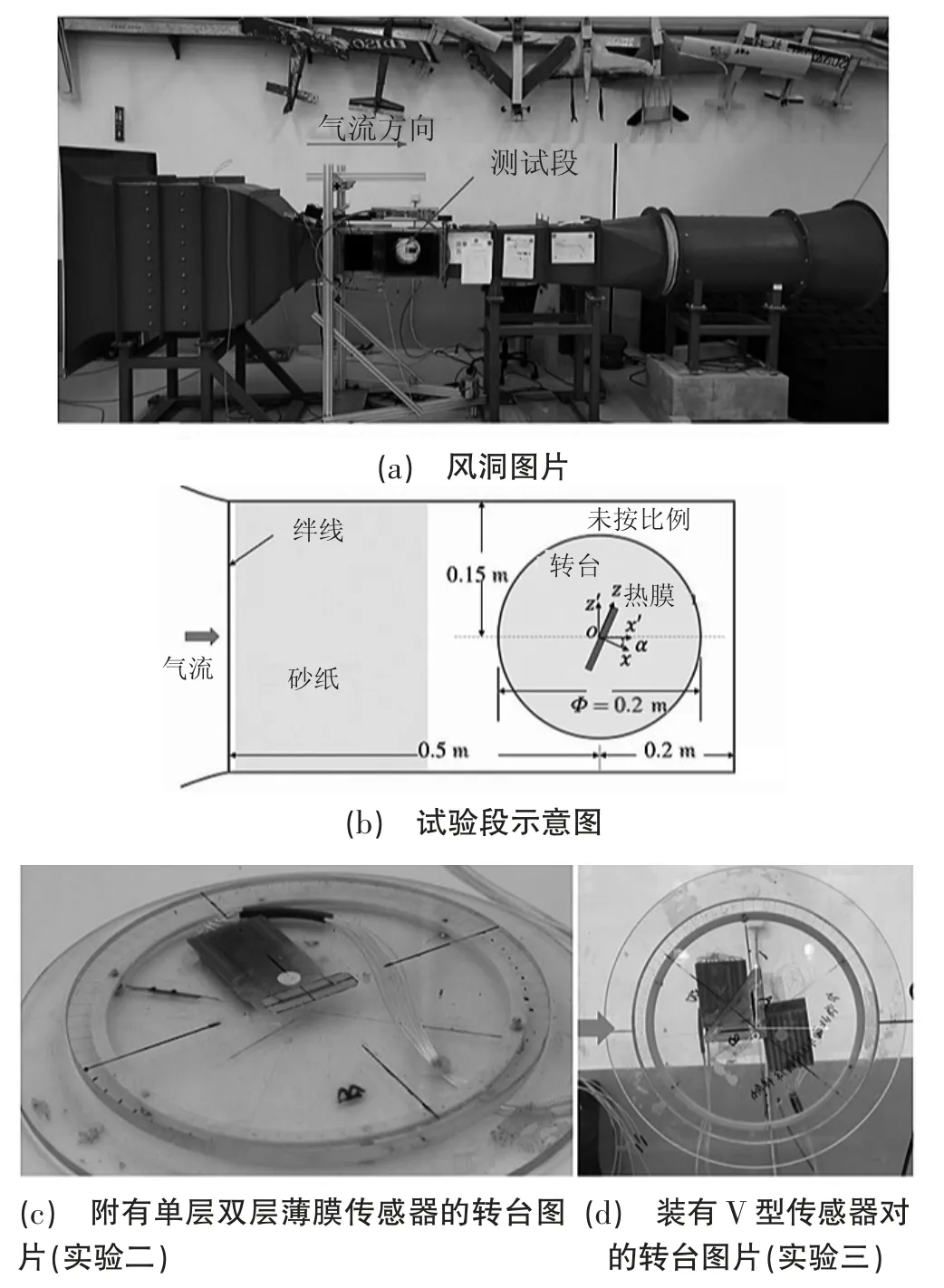
圖5 雙組分免標定技術驗證試驗示意圖

3.3 實驗三：驗證雙組分免標定技術

本實驗驗證了使用一對未經標定的雙層熱膜傳感器構成的新型壁面剪應力傳感器的有效性，該傳感器的圖片如圖5（d）所示。如圖3 所示，即2 個具有相同幾何形狀的傳感器垂直放置，并以V 形相互靠近。傳感器安裝在轉臺的中心，此處的流動條件與實驗二中的流動條件相同。

4 結束語

首先介紹了剪應力傳感器的標定與熱膜傳感器的測量原理，之后提出了一種基于方向靈敏度的局部雙組分壁面剪應力測量技術，該技術使用一對相互垂直放置的未經標定的雙層熱膜傳感器，利用從傳感器傳遞到流體的熱通量來確定壁面剪應力的大小和方向，因此無需標定。通過理論和實驗方法證明了嵌入式熱膜傳感器的方向靈敏度（對偏航角α 的靈敏度）為cos1/3α。